应用改进K-means算法的批量定制服装号型分类

王 旭, 齐雪良, 袁惠芬, 刘新华

(安徽工程大学 a.纺织面料安徽省高校重点实验室； b.纺织行业科技公共服务平台, 安徽 芜湖 241000)

应用改进K-means算法的批量定制服装号型分类

王 旭a, b, 齐雪良a, 袁惠芬a, 刘新华a, b

(安徽工程大学 a.纺织面料安徽省高校重点实验室； b.纺织行业科技公共服务平台, 安徽 芜湖 241000)

为合理确定批量定制服装的版型数量, 运用K-means算法, 以4个测量项目(身高、胸围、腰围、领围)为分类变量对347名男性进行聚类分析.分别以国标和非国标号型对初始聚心选择和聚类数的确定进行探讨, 并以Calinski-Harabasz(CH)指标、变异系数和相对偏差比较了国标和非国标号型的聚类效果.研究结果表明, 运用最大最小距离法确定初始聚心的非国标号型分类结果与国标 GB/T 1335.1—2008分类结果对比, 在相同CH值时, 服装版型数由26减少到18, 身高、胸围、领围和腰围相对偏差超过3%的比例分别从5.48%, 39.48%, 7.49%, 60.52%降低到0.58%, 8.07%, 3.17%, 12.97%.测量项目波动性从大到小依次为腰围、领围、胸围和身高.

K-means算法；批量定制；号型分类；聚类分析

批量定制生产具有快速和低成本的优点, 正逐渐成为定制服装企业的主流生产模式.而号型归档是批量定制生产的重要前提.服装非定制生产模式主要遵照国标及企业标准, 根据身高和胸围的区域覆盖率并适当增删体型类别以确定号型.批量定制生产时可采用样衣试穿归档法、人体净尺寸归档法及按被测者成衣尺寸归档法[1].实际上, 批量定制生产既可依据量体数据按国标号型归档, 又可依据聚类分析的结果以非国标规格归档.为提高归档效率, 已开展的服装号型归档研究主要有归档结构链、最短距离法和聚类分析等.文献[1]将个体尺寸融入企业已有规格, 提出了上、下装归档结构链方案.文献[2]以男西服64个国标号型为基准点, 采用择近原则归档, 取得了较好的效果.文献[3]开发出基于最短距离法和Web Service技术的号型归档系统, 并通过实例进行验证. 文献[4]以胸腰差为实例, 参考GB/T 1335—2008, 采用K-means算法分析219名女性体型, 并讨论了最佳聚类数及迭代次数的确定.文献[5]基于不同地区女大学生体型, 以胸腰差、胸腰比、胸腰型和体型丰满度罗氏指数分组搭配进行K-means聚类分析, 结果表明以胸腰差和罗氏指数为分类变量时分类效果最好.文献[6]对192名女模特人体数据进行主成分和聚类分析, 提出了女模特身高、胸围、腰围、臀围和腰高等体型标准.上述研究表明, 合适的归档算法是提高号型分类效率和效果的关键.K-means算法适合大批量数据且分类速度快, 但分类结果易受初始聚心及分类数的影响.对于号型归档问题, 即以不同的规格作为初始聚心来确定号型分类.

为了确定批量定制服装合理的版型数量,分别以国标规格及采用最大最小距离法选择的非国标规格作为初始聚心, 对347名成年男性人体数据进行K-means聚类, 并以Calinski-Harabasz(CH)指标、变异系数和相对偏差对聚类效果进行评价.研究结果为确定批量定制服装合理的版型数量和提高分类效果提供参考.

1 试验部分

1.1 试验数据

样本为347名30岁以上海某机关成年男性, 根据所定制服装款式的要求, 测量项目包括身高、胸围、腰围、领围.

1.2 试验数据分析

批量定制服装号型分类研究分析流程如图1所示, 包括数据采集、数据预处理、确定初始聚心、聚类分析、聚类结果评价及确定版型数.

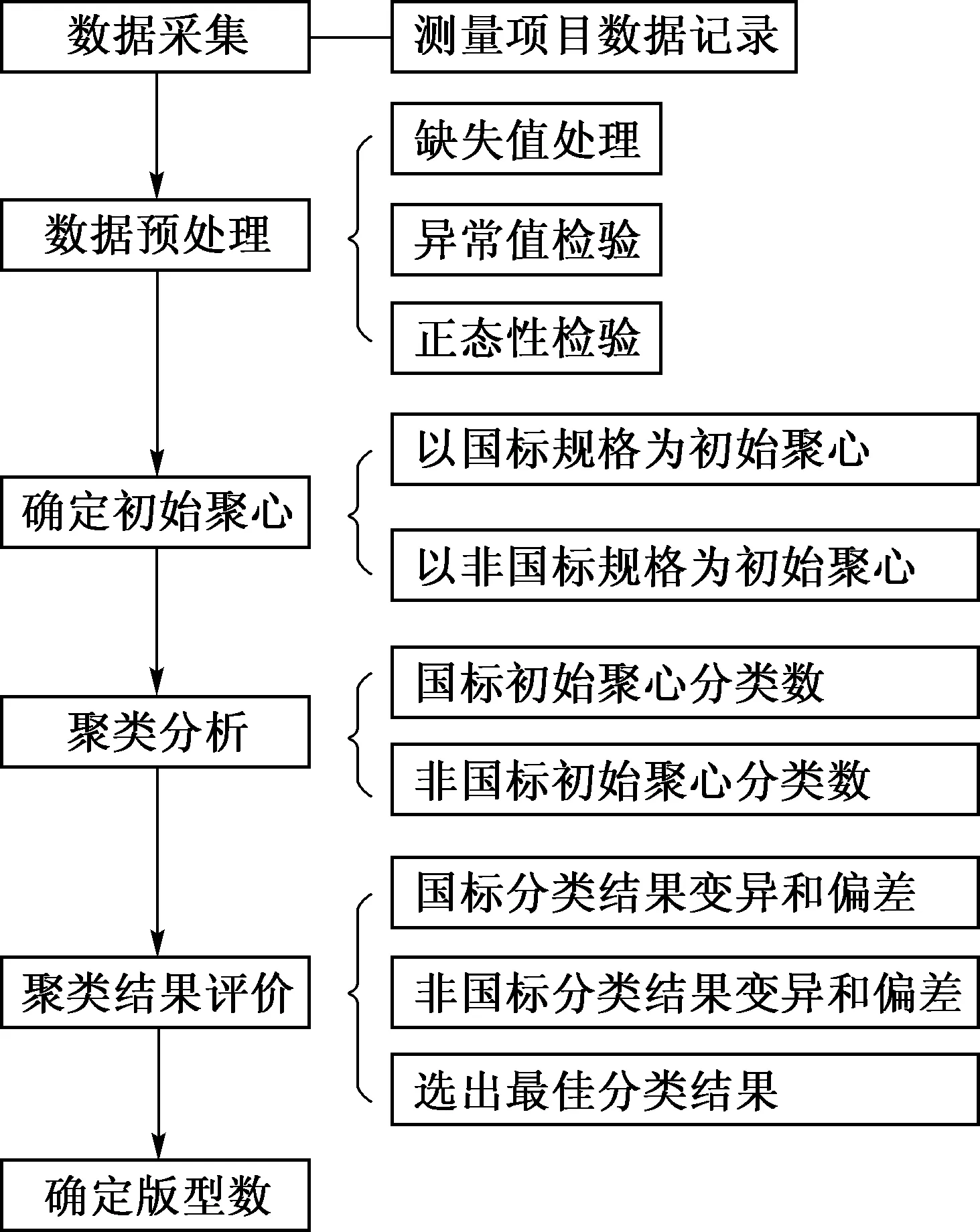
图1 数据分析流程图Fig.1 Flowchart of data analysis

1.2.1 数据预处理[7]

若存在缺失值, 则删除整条数据.根据异常值Walsh检验法[8], 样本容量为n时, 若可疑异常值x为数据中r个最小或最大值, 计算式(1)或(2), 当W1或W2<0时, 则该r个最小或最大数据为异常值.

W1=xr-(1+b)xr+1+bxk

(1)

W2=-xn+1-r+(1+b)xn-r-bxn+1-k

(2)

其中:b、k值分别按式(3)、(5)计算.

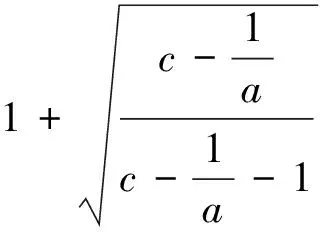
(3)

(4)

k=r+c

(5)

其中: c值根据样本容量n按式(4)确定，Trunc为取整函数；a为显著性水平, 默认取0.05.

为满足K-means聚类分析对数据的要求[4], 按式(6)进行数据正态性判定[8].

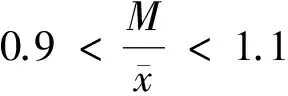
(6)

1.2.2 改进的K-means算法

结合经典K-means算法[9]按最大最小距离法对初始聚心选取进行改进, 步骤如下:

(1) 取距样本中心最近的样品作为第一初始聚心Z1；

(2) 取距Z1最远的样品作为第二初始聚心Z2；

(3) 计算样品Xi与Z1和Z2间的距离di1和di2, 若max(ΔdN)>θ‖Z1-Z2‖, 则样品Xi为第三聚类中心Z3(θ为比例系数, max(ΔdN)为第N次聚类中心最大改变量)[4], 否则归入到其中一个聚类中；

(4) 重复操作, 直至找不到符合条件的新聚心为止.

1.3 分类数确定及分类效果评价

分类数通过CH指标并结合国标分类结果确定.分类效果以变异系数和相对偏差衡量.

1.3.1 CH指标计算

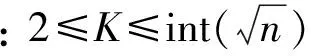
(2) 分别按式(7)、(8)计算各类的类内距离之和D1及类间距离之和D2；

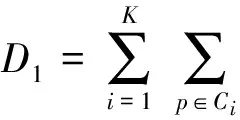
(7)

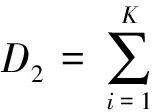
(8)

(3) 按式(9)计算CH值, CH值越大则表明聚类效果越好.

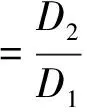
(9)

1.3.2 变异系数和相对偏差计算

变异系数CV和相对偏差d分别是衡量数据变异程度和偏离均值程度的指标, 计算式如式(10)、 (11)所示.

(10)

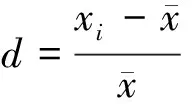
(11)

2 结果与讨论

2.1 数据预处理

样本中347个样品无缺失值, 其Walsh和正态性检验如表1和2所示.表1中,b、c、k是当r=1,n=347, 取显著性水平a=0.05时, 由式(3)～(5)计算得到.W1和W2分别由式(1)、(2)计算得到.Walsh检验表明, 347个样品中最小和最大值均不异常, 说明样本无异常值.由表2可知, 样本的4个测量项目均满足式(6), 说明各测量项目符合正态分布.

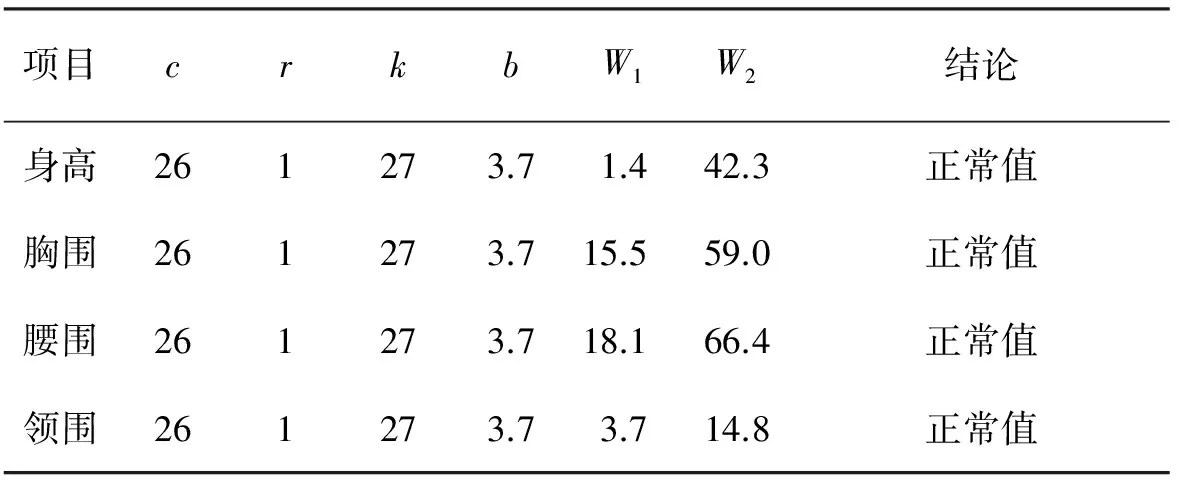
表1 数据Walsh检验

表2 数据正态性检验

2.2 以国标规格为初始聚心的聚类分析

以国标规格为初始聚心的K-means聚类, 实质上是初始聚心为给定的国标规格点, 按择近原则进行的一次性分类, 分类过程聚心的位置不发生变化.以身高和胸围为例的K-means聚类示意图如图2所示.图中黑色圆点为按国标5.4系列确定的初始聚心, 待分类的数据将按择近原则归档, 即当数据在聚心周围的阴影区域时, 被分入该档.结合身高、胸围、腰围国标号型和某定制服装企业胸围和领围的搭配经验, 选择初始聚心为46个.运行SPSS软件, 读入初始聚心, 执行仅分类的K-means聚类, 结果如表3所示, 347个样品被分为26类.

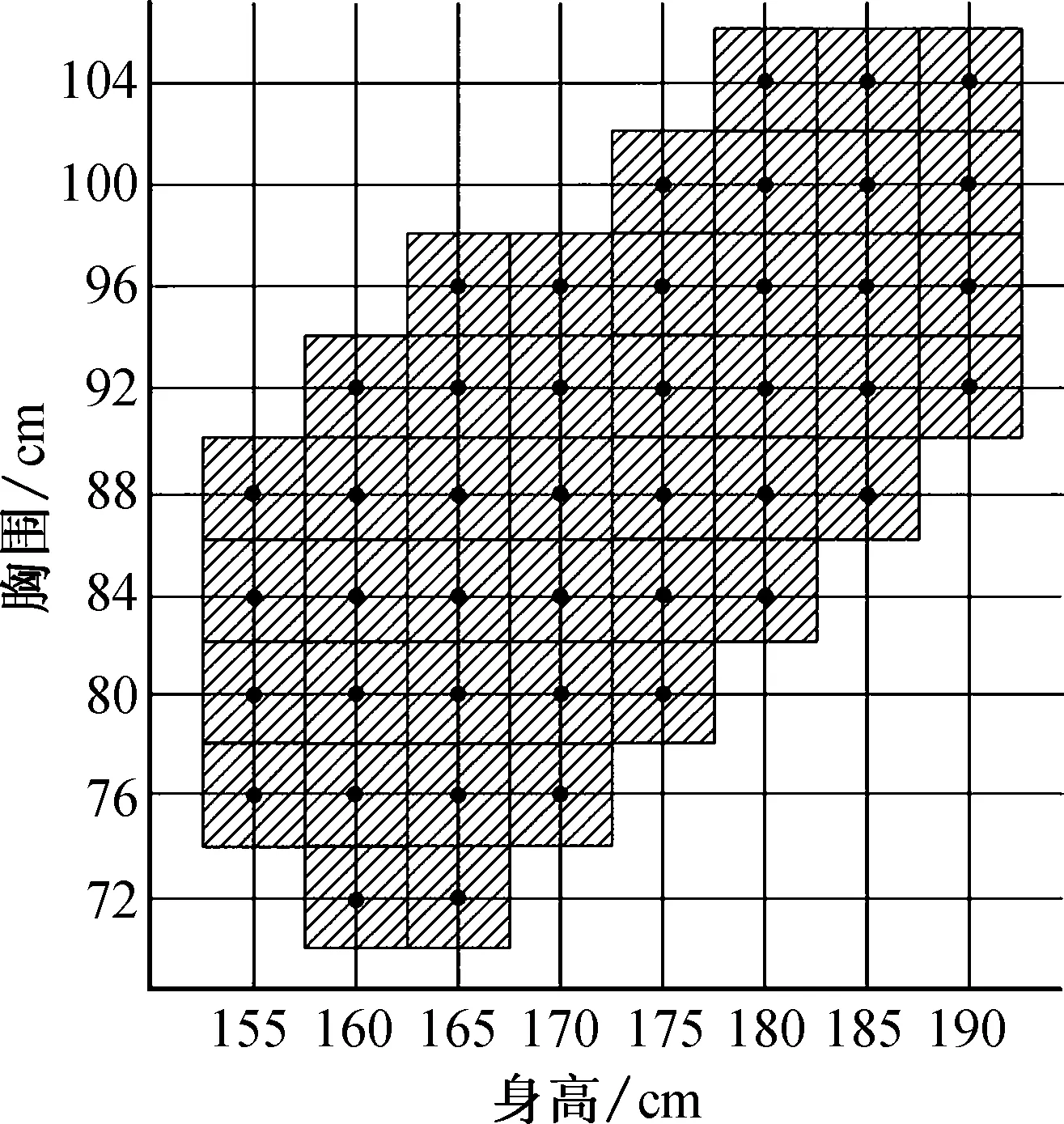
图2 以国标规格为初始聚心的K-means聚类示意图Fig.2 The scheme of K-means clustering with national standards initial clustering center

表3 以国标规格为初始聚心的分类结果

2.3 以非国标规格为初始聚心的聚类分析

为了与国标分类(26类)的结果对比, 当θ=0.172, 按1.2.2节的最大最小距离法选择非国标规格26个初始聚心Zi(i=1, 2, …, 26), 如表4所示.

表4 以非国标规格为初始聚心的分类结果

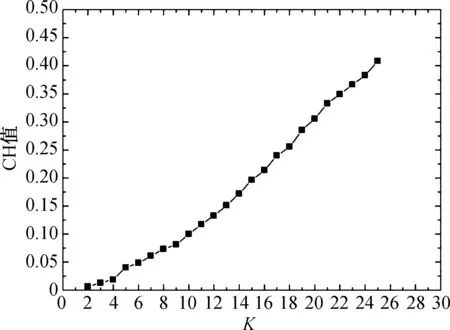
图3 以非国标规格为初始聚心的聚类效果Fig.3 The CH value of K-means clustering with non-national standards initial clustering center

运行SPSS软件读入表4所示的26个非国标规格初始聚心(Z1,Z2, …,Z26), 执行K-means聚类, 并根据聚类结果分别计算不同聚类数K时的CH指标, 如图3所示.通常CH值越大, 聚类效果越好.批量定制的原则是根据定制数据分类结果进行的成衣化生产.为降低成本, 可在满足一定聚类效果的前提下, 尽可能减少版型数量.本次聚类以国标分类(26类)为基准(CH值=0.247), 按CH值接近国标分类为原则, 确定非国标聚类数K=18(CH值=0.256), 即该批次347个样品, 可依据表4的前18个初始聚心(Z1,Z2, …,Z18), 聚类为

18个版型(分类结果如表4所示), 其中括号内的数值为根据类内样品计算的指标均值取整的结果, 即版型设计时可参考类内样品均值进行.

综上所述说明, 以非国标形式比以国标形式选择的初始聚心, 在聚类效果一致时, 具有更少的版型数.但同时注意到, 数据反映的成年男性, 存在少量体型特殊的个体, 从而影响分类效果, 可以通过增加聚类数或对该类个体单独处理从而保证服装的合体.

2.4 国标规格与非国标规格聚类效果对比

CH指标高低仅从数值上反映聚类效果的好坏, 而评价4个测量项目在各分类中的变异系数和相对偏差对生产更具有实际意义.表5为按照国标和非国标分类结果的各类变异系数和相对偏差.其中测量项目变异系数范围由18个分类中最小和最大变异系数确定.测量项目平均变异系数是各类别变异系数的均值.相对偏差比例是超过一定相对偏差值的样品所占的百分比.

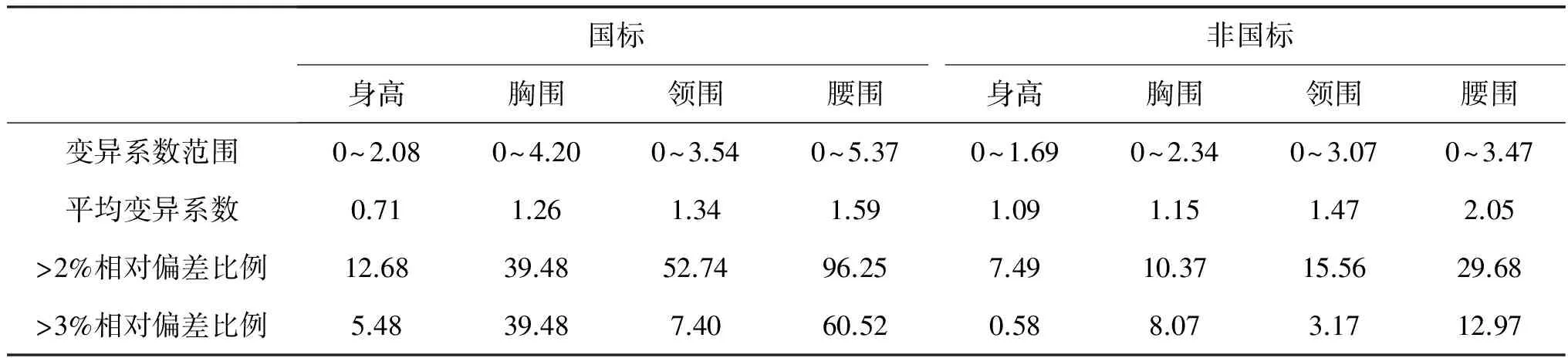
表5 国标与非国标分类变异系数与相对偏差

由表5可知, 非国标分类结果中4个测量项目的变异系数范围均小于相应的国标分类结果, 表明以非国标方式聚类, 类内样品测量项目变异较小.但对平均变异系数而言国标聚类略小于非国标聚类, 其原因是国标分类数大于非国标分类数.在4个测量项目中, 变异系数从大到小依次为腰围、领围、胸围、身高, 说明样本反映的成年男性群体的腰围变异系数较大.

根据国标档差在4个测量项目中, 相对偏差小于3%才具有实际意义.在各测量项目中, 样品相对偏差>2%的样品比例, 从大到小依次为腰围、领围、胸围、身高.这一结果和变异系数趋势一致.其中腰围相对偏差>2%样品比例高达96.25%, 而非国标只有29.68%.其原因在于, 通常按国标分类时, 以腰围±2 cm的绝对偏差划分, 以170/92 A为例, 如取腰围84 cm, 则存在大量腰围值绝对偏差超过±1.68 cm的样品, 从而导致超标比例高.其他3个项目国标相对偏差>2%样品比例分别为12.68%, 39.48%, 52.74%, 而对应非国标比例分别为7.49%, 10.37%, 15.56%.腰围相对偏差> 3%的国标和非国标样品比例分别减少到60.52%和12.97%, 其他3个项目超标比例国标为5.48%, 7.49%, 39.48%, 对应的非国标为0.58%, 3.17%, 8.07%.

综上分析, 非国标的变异系数和相对偏差均小于国标, 表明非国标分类样品与版型偏离程度小, 聚类效果更好.

3 结 论

(1) 以最大最小距离法产生的非国标规格初始聚心, 结合K-means算法的聚类结果, 在CH值相同时, 比传统国标分类具有更少的版型数量.

(2) 样品和版型的变异系数和相对偏差对比分析表明, 以非国标规格为初始聚心的聚类效果优于国标规格.4个测量项目中变异系数及相对偏差从大到小依次为腰围、领围、胸围和身高.

[1] 徐继红, 张向辉, 张文斌. 定制服装号型归档与裁剪方案数字化研究[J].东华大学学报(自然科学版), 2003, 29(2): 37-42.

[2] 王建萍, 李月丽, 喻芳. 基于择近原则的服装号型数字化归档方法[J].纺织学报, 2007, 28(11): 106-110.

[3] 毋涛, 王银. 服装批量定制量体服务系统的设计与实现[J].陕西科技大学学报, 2011, 29(8): 54-56.

[4] 方方, 王子英. K-means聚类分析在人体体型分类中的应用[J].东华大学学报(自然科学版), 2014, 40(5): 593-598.

[5] 郑艳, 张欣. 我国三地区女大学生体型分类研究[J].西安工程科技学院学报, 2004, 18(3): 210-214.

[6] 张宁, 王宏付. 基于三维人体测量的江浙女模特体型分类[J].纺织学报, 2012, 33(6): 71-75.

[7] 齐静, 李毅, 张欣. 我国西部地区青年男性体型描述与体型分类研究[J].纺织学报, 2010, 31(5): 107-111.

[8] 郁崇文, 汪军, 王新厚. 工程参数的最优化设计[M].上海: 东华大学出版社, 2003: 4-6.

[9] 周世兵, 徐振源, 唐旭清. 新的K-均值算法最佳聚类数确定方法[J].计算机工程与应用, 2010, 46(16): 27-31.

[10] 刘燕驰, 高学东, 国宏伟, 等. 聚类有效性的组合评价方法[J].计算机工程与应用, 2011, 47(19): 15-17, 30.

(责任编辑: 杜 佳)

Mass Customization Clothing Shape Classification by Improved K-means Algorithm

WANGXua, b,QIXuelianga,YUANHuifena,LIUXinhuaa, b

(a. Anhui Provincial Key Laboratory of Textile Fabric；b. The Science and Technology Public Service Platform for Textile Industry, Anhui Polytechnic University, Wuhu 241000, China)

In order to determine reasonable pattern number of mass customization clothing, the 347-male body data was analyzed based on K-means clustering algorithm with four classified variables such as height(H), bust circumference(BC), waist circumference(WC) and collar circumference(CC). Classification methods of the non-national standard shape and national standard shape to research selection of initial centers and determination of the optimal clusters, and evaluated the cluster in Calinski-Harabasz(CH) index, coefficient of variation and relative deviation. The results show that the clothing pattern number of 26 reduces to 18 and relative deviation(H, BC, CC, WC) is decreased from 5.48%, 39.48%, 7.49%, 60.52% to 0.58%, 8.07%, 3.17%, 12.97%, when the CH index is same and compared to the non-national standard shape that maximum-minimum distance algorithm is adopted to determine the initial centers with national GB/T 1335.1—2008. The volatility of measuring items from big to small is WC, CC, BC and H.

K-means algorithm; mass customization; shape classification; clustering analysis

1671-0444 (2017)03-0364-06

2016-05-12

纺织面料安徽省高校重点实验室开放基金资助项目(2015FZ001)；安徽工程大学研究生实践与创新资助项目(2015)

王 旭(1973—)，男，安徽六安人，副教授，博士，研究方向为纺织与服装数字化. E-mail:wangxu_ahpu@hotmail.com

TS 941.1

A