基于SVM和有监督描述子学习算法的脑MR图像颅骨分割方法∗
黄勇其 史文博 周志勇 庞树茂 佟宝同 赵凌霄 戴亚康
(1.中国科学院苏州生物医学工程技术研究所苏州215163)(2.中国科学院大学北京100049)(3.北京师范大学北京100875)(4.南方医科大学广州510515)
基于SVM和有监督描述子学习算法的脑MR图像颅骨分割方法∗
黄勇其1,2史文博3周志勇1庞树茂4佟宝同1赵凌霄1戴亚康1
(1.中国科学院苏州生物医学工程技术研究所苏州215163)(2.中国科学院大学北京100049)(3.北京师范大学北京100875)(4.南方医科大学广州510515)
神经电流源定位研究首先要解决EEG、MEG正问题的计算。在求解MEG和EEG正问题的过程中,为了精确地计算传导矩阵,常常需要对脑组织进行分层建模。在脑MR图像中,虽然软组织能被清晰地成像,但颅骨却由于缺少氢而呈现低灰度值,从而很难自动分割出颅骨。因此如何从脑MR图像中准确、自动分割出颅骨是解决MEG、EEG正问题的关键。为解决上述问题,提出一种基于支持向量机的自动脑MR图像颅骨分割方法,提取病人MR图像的全局特征和局部特征进行训练,并结合有监督描述子学习算法SDL,将得到的特征矩阵进行压缩,去掉冗余的特征,得到一个紧凑的特征描述,最终利用SVM从脑MR图像中自动识别出骨骼。实验结果表明,采用支持向量机结合有监督描述子学习算法的分割方法与仅使用支持向量机和仅使用数学形态学方法相比,分割精度进一步提升,Dice分割精度分别为0.832,0.798,0.482,从而解决了从脑MR图像自动分割颅骨的任务,并为解决EEG和MEG正问题的研究奠定基础。
颅骨分割;支持向量机;有监督描述子学习算法;特征提取;特征压缩
Class NumberTP391
1 引言
随着MEG和EEG技术的快速发展,脑磁和脑电信号在研究脑神经生理活动中扮演着越来越重要的角色。在EEG和MEG神经电流源定位的正问题计算中,以往通常利用简单的球模型[1]来模拟大脑结构,进而求解传导矩阵。然而,人脑结构异常复杂,颅骨凹凸性各异,难以从简单的球模型中求得传导矩阵的解,进而定位出神经电流源的位置。因此若能从人脑MR图像中提取出颅骨结构,就能针对具体的个人构建出一个真实的头模型[2],从而准确解决神经电流源定位的问题。
真实的颅骨模型为解决EEG正问题提供极大的便利,到目前为止,有不少有关大脑分割的研究,例如文献[3]中作者提出一种基于贝叶斯分层混合模型的方法成功实现大脑FMRI图像的自动分割;文献[4]中作者基于最大后验概率对脑MR图像进行三维分割,成功分割出脑白质与灰质。然而仅有少数的颅骨分割算法被提出。例如Heinonen等[5]用阈值和区域生长方法从MR图像中分割出骨骼,该方法对后脑等形状较规则的区域能形成较好的分割,但对特定的骨骼区域,如眼廓,因为部分容积效应的原因并不能很好地分割出骨骼;Rifai等[6]应用一种可形变模型从MR图像中分割出骨骼,该方法在仿真MRI图像中取得了较好的分割结果,但在真实MRI图像中,可形变模型会带来不确定边界的情况,例如分割的结果里面混合了皮肤,肌肉,眼睛,内耳的组织;Chu和Takaya[7]用阈值和高斯拉普拉斯算子对连续横断层的头皮-颅骨的边界和颅骨-大脑的边界进行检测,该方法对于大脑颅骨外边界能达到较好的检测,对部分头皮-颅骨的边界也能较好区分,但对于结构较复杂区域,如眼窝,内耳区域等不能明显进行区分;B.Dogdas等[8]运用数学形态学开操作闭操作等方法将颅骨分割出来,该方法能较好地分割出大脑区域,对颅骨外层也能取得较好分割结果,但数学形态学开闭操作的方法受限于需要人为地设定一个阈值,鲁棒性并不高。
图像的特征压缩能大大缩短颅骨分割的时间,目前比较流行的特征压缩方法有:Golub和Van Loan[9]提出的奇异值分解(SVD)方法,该方法用特征矩阵的方式取代特征向量的表示方法,在降维的同时保留了数据的关键信息,实现了原始数据的低维近似描述。Dhillon和Modha[10],Srebro和Jaakko⁃la[11],Castelli等[12],都对数据压缩进行了广泛的研究,在提取相似度最高的数据和移除噪声方面取得了较好的结果,然而随着数据量的增大,它们的算法均不同程度地受到时间复杂度和空间复杂度的限制。Achilioptas和McSherry[13]采用随机采样的方法来加速奇异值分解以得到原始数据的低维近似描述,然而该研究的效率很大程度上取决于数据矩阵的能谱结构。另一个应用广泛的数据压缩方法是压缩感知[14],压缩感知理论利用少量的线性测量值就能感知信号的初始结构,然后通过求解最优化问题实现信号的精确重构。尽管压缩感知得到了较广泛的应用,但仍有一些需要解决的问题,例如在稀疏表示方面,如何引入流形结构,在重建算法方面,如何解决重建时间过长的问题等。
为了从脑MR图像中分割出颅骨,解决EEG、MEG源成像问题,本文提出一种基于支持向量机结合有监督描述子学习算法SDL的自动脑图像颅骨分割算法,以图像的局部和全局信息作为输入,提取MR图像的概率图谱、邻域强度、统计矩等有代表性的多个特征值,并利用SDL算法对得到的特征矩阵进行特征选择,去除冗余的特征值,最后将得到的经压缩后的特征矩阵输入到支持向量机进行训练,达到自动分割脑MR颅骨的目的,并与仅用支持向量机的方法和数学形态学的方法进行对比,证明了本方法的有效性。
2 方法
本文分割方法主要包括三部分内容,首先将图像数据进行配准并提取多个关键特征,再利用有监督描述子学习算法(SDL)进行特征压缩,最后利用支持向量机SVM训练得到的特征矩阵。
2.1 图像特征提取
机器学习算法最重要的步骤之一就是特征的选取,特别地,随着数据量的增加,特征空间的扩大,大小合适的特征数量就显得尤为重要。这样的特征矩阵不仅能减少SVM训练时间,而且也不会出现过拟合的现象。
本文选取的特征主要包括如下三类特征:
1)概率图谱:该特征为全局特征,选取数据集中的某个病人的CT图像作为参考CT,并将其他病人的CT图像以刚性配准的方法配准到参考病人的CT图像中,然后以300H单元的阈值分割出骨骼。再从分割出的所有病人的CT颅骨图像中求得平均值,得到的结果即为概率图谱。结果如图1所示。
算法的全部数据都是基于参考MR坐标系的,因此需要将得到的概率图谱配准到参考MR坐标系中。配准流程和训练流程如图2所示,每个病人的训练CT均采用刚性配准的方法配准至相应的MR中,并最终配准至参考MR。待分割目标MR也要配准到参考MR中,之后再利用本文算法进行分割。

图18组CT图像分别分割颅骨后求得的平均值,图中为第34层,取值范围[0,1]

图2来自不同病人数据的多模态的配准概述
2)邻域强度:以体素为中心,提取每个坐标轴的7个体素的灰度值作为局部特征(总共19个灰度值)。在建立体素模型时,不同大小的体素区域其三维模型差别非常明显,当体素区域过小时,不能准确表达三维图像的表面形态,而当体素区域过大时,则会占用大量的物理空间,造成浪费,因此选择合适的体素区域非常重要。本文选择图3所示体素区域用以获取邻域强度特征值。

图3用于计算邻域强度的体素区域
3)统计矩:为了反映图像的局部纹理特征,选取统计矩μn作为第三个特征值,计算如下:

其中zv表示区域V中的体素v的灰度值,区域V用一个边长为3体素的立方体区域表示,体素区域的大小选择同邻域强度,本文选取26-邻域的体素区域用以计算统计矩,如图4所示。m为该区域的平均灰度值,其中n≥2,n取2时为二阶矩,即方差,度量的是图像边界偏离体素区域均值的程度,三阶矩描述的是图像纹理灰度的起伏分布,四阶矩描述纹理灰度的反差,五阶矩和更高矩不容易和图像的直方图连续起来。本文取二阶矩作为第三个图像特征值。
2.2 有监督描述子学习算法
有监督描述子学习算法[15](SDL)是一种特征表示学习法,该方法能去除不相关和冗余的特征值,并将高维的特征转换为较低维的特征表示,最终得到一个紧凑且高区别度的特征表示。
对于给定的特征向量{X1,X2,…,XL},和对应的标签值{Y1,Y2,…,Yn},L表示特征向量的个数。目标是找到变换矩阵W∈RM×m,V∈RN×n,使得向量Di∈Rm×n经过变换WDiVT近似于特征向量Xi。即相当于求解如下最优问题:

为了提高近似特征值的精度,引入如下有监督的流形正则化项:

其中Sij为一核函数,如下式所示:
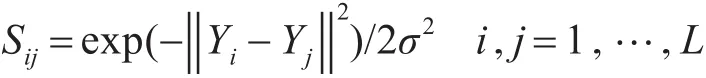
结合式(1)和式(2)可得:

β∈(0,∞)为一常量。
为了求得上述结果,采取迭代优化的方法,经优化Di=WTXiV,结合矩阵的秩,式(3)转化为求解如下最大值:

对于任意给定一个向量V,可根据下式求得最优的向量W:

其中

同样的,给定一个向量W,可根据下式求得最优的向量V:

其中

通过单一值分解方法(SVD)可求得式(5)和式(7)的解。
本文首先利用有监督流形正则化算法(SMR)[16]生成所得特征矩阵的低维近似矩阵描述,再利用有监督描述子学习算法训练得到的低维特征,除去冗余和不相关的特征值,最后得到一个紧凑的区别度高的特征描述。
3 实验结果及分析
3.1 实验准备
在实验中,本文共选取8组临床MR图像进行实验,并在Matlab R2013a的编程环境下进行实验,采用LIBSVM[17]工具箱进行编程训练。然后将SDL特征压缩后得到的分割结果和特征压缩前得到的分割结果进行对比,并与数学形态学方法、线性判别式分析法(LDA)、主成分分析法(PCA)分割结果进行对比,分别计算其Matthews相关系数(MCC),Dice相关系数(Dice),真阳性率(Pt),假阳性率(Pf)。
评价参数简介:
1)Matthews相关系数(MCC)。定义如下:

其中P11,P10,P01,P00由如下混淆矩阵定义给出:

由式(9)可知,MCC取值范围在[-1,+1],值越高,代表两幅图像的相似程度越高。
2)Dice相关系数(D)。定义如下:

其中,SMR表示用本文方法从MR图像分割得到的颅骨图,SCT表示用阈值分割方法从脑CT图像中分割得到的颅骨图。
3)分割误差(Pt和Pf)定义为:。其中,Nvp为标准图像(阈值分割结果)中标记为分割目标的像素个数和;Nuvp为标准图像中被标记为非分割目标的像素个数总和;TN为本文分割结果中正确分割的像素数和,FN为本文分割结果中错误分割的像素数和。
3.2 实验结果分析
特征的有效性决定了分割的精确度,为验证所提取特征的有效性,对本文提出的三类特征进行不同组合并利用SVM进行训练,得到如图5所示的分割准确率与不同特征组合的关系图。其中1代表概率图谱值,2代表邻域强度值,3代表统计矩,1+2表示概率图谱与领域强度值的组合,以此类推。从图中可以看出,概率图谱特征值在识别颅骨区域和非颅骨区域上具有很强的代表性,其与其他特征值的不同组合均显示很高的分割准确率。而仅使用领域强度或统计矩或两者的组合作为特征,识别率并不高,不能达到区分颅骨和非颅骨的目的。本文选择三种特征的组合确保了分割的准确性。
为了降低冗余特征对分类器的影响并获取合适的特征维数,首先利用SDL方法对得到的21维特征矩阵进行不同程度的压缩,随后对另两种压缩方法PCA和LDA进行实验,得到支持向量机的分类准确率随压缩特征维数的变化关系图。从图6可看出,在本文方法中,SDL比LDA和PCA取得的分割准确率要高,并且可看出当特征维数压缩到8维至14维可以取得较高的分割准确率。

图5不同特征组合与分割准确率的关系图
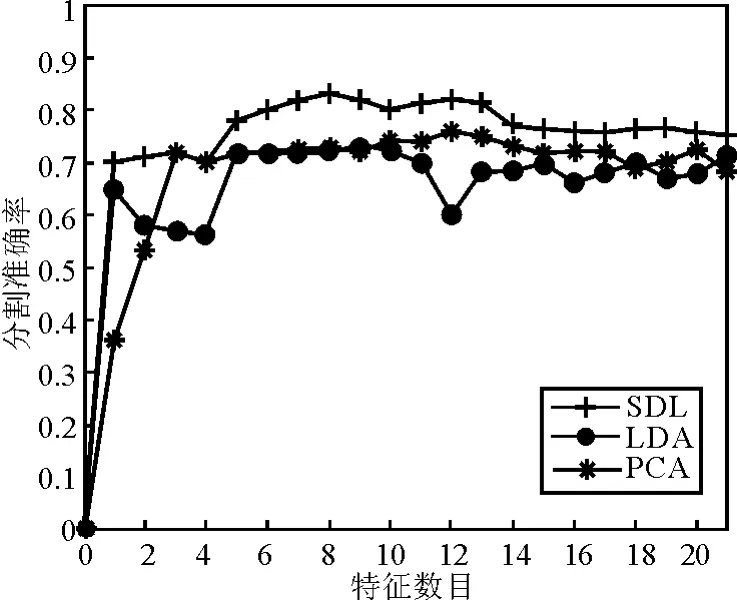
图6SVM分类准确率与特征数目的关系
随后分别与特征压缩前的SVM分割结果和运用数学形态学方法得到的分割结果进行对比,得到五种分割方法的数据对比,本文选择将特征矩阵压缩至9维进行对比实验。在以上Matthews相关系数(MCC)、Dice相关系数(D)、分割误差(Pt和Pf)中,MCC、Dice和Pt的数值越高,表示分割结果越好,两幅图像的相似程度越高,而Pf数值越低表示分割结果越好,相似程度越高。
图7为分割结果对比图,均选取了同一层面进行对比分析,图中灰色区域标识分割结果与CT阈值分割结果的差异之处,从图中可以看出,特征压缩前,分割的误差主要集中在大脑两侧区域和后脑区域,经LDA和PCA特征压缩后的分割结果改善不明显,而经过SDL特征压缩后再进行分割,虽然后脑区域仍存在些许误差,但较好地解决了大脑两侧的分割问题,进一步提高了分割精度。而从数学形态学的分割结果看,其分割结果明显劣于特征压缩前的分割结果和特征压缩后的分割结果。从下图中也可以明显地看出数学形态学分割结果与CT阈值分割存在较大的误差。在大脑的各个部位均不能很好的达到分割目的。

图7分割结果对比图,图中均为第72层图像
为了定量分析五种分割方法的区别,利用直方图的形式将五种分割方法的评价参数进行对比分析。如下列直方图所示,实验中SDL特征压缩后MCC相关系数平均值达到0.788,Dice系数均值为0.832,均高于特征压缩前的0.741、0.798,LDA方法的0.69、0.74,PCA方法的0.72、0.73,数学形态学方法的0.478和0.482,Pt和Pf进行对比也显示了SDL特征压缩后的分割优势。

图8五种分割方法MCC对比
图8为五种分割方法的MCC结果对比直方图,从图中可以明显看出经过SDL特征压缩后取得的分割结果要高于特征压缩前的结果(即原始数据的分割结果),同时高于LDA和PCA方法的结果,且远高于数学形态学方法分割结果,其中LDA和PCA方法分割精度相似。类似于MCC结果,五种分割方法Dice系数直方图如图9所示,从图中可知数学形态学分割结果较差,Dice均值只有0.482不足0.50,LDA和PCA分割结果次之,分别为0.74和0.73,压缩前的分割结果Dice均值为0.798,SDL特征压缩后的分割结果效果最好,Dice均值达到了0.832。

图9五种分割方法Dice对比
图10为五种分割方法的Pt对比直方图,Pt代表五种方法的正确分割颅骨数与标准图像中标记为颅骨的数目之比,数值越高代表分割精度越好,两幅图像相似度越高。从图中可看出采用支持向量机SVM的方法取得的分割效果要优于数学形态学的分割方法。

图10五种分割方法Pt对比
同图10,图11为五种分割方法的Pf对比直方图,Pf代表三种方法的错误分割颅骨数与标准图像中标记为非颅骨的数目之比,数值越高代表分割精度越低,两幅图像相似度越低。如图所示,数学形态学方法的Pf值要高于其他四种方法,而经SDL特征压缩后的Pf值最小,代表分割结果最好。

图11五种分割方法Pf对比
综上所述,本文提出的算法成功地从脑MR图像中自动分割出颅骨,并取得了较高的精确度,较好地吻合了真实的大脑头模型,为解决MEG/EEG的源成像问题提供了方法指导。
4 结语
本文提出了一种基于支持向量机和有监督描述子学习算法的自动脑MR图像颅骨分割方法,创新之处在于提出多特征值以区别颅骨区域和非颅骨区域,在确保特征值的有效性基础上将支持向量机SVM方法与有监督描述子学习算法结合在一起,去除了冗余特征对分类器的影响,进一步提高了分割精确度。首先提取待分割MR图像的全局特征(概率图谱值)、局部特征(邻域强度和统计矩),构建出特征矩阵,并利用有监督描述子学习算法进行特征压缩,去除冗余和不相关的特征值,得到降维后的特征矩阵,在本文中特征压缩前得到的特征矩阵是21维的,经有监督描述子学习算法压缩后的特征矩阵维度为9,极大地降低了特征矩阵的维度,最后利用支持向量机SVM对21维的特征矩阵和9维的特征矩阵进行训练,最终实现自动分割脑MR图像颅骨的目的。之后分别将SDL特征压缩后的分割结果与特征压缩前的分割结果和LDA、PCA、数学形态学的分割结果进行对比,分别求取评价参数Matthews相关系数(MCC)、Dice相关系数(D)和分割误差(Pt和Pf)进行对比,并利用柱状图进行数据对比分析,从柱状图中可以明显看出采用支持向量机的训练方法进行脑MR颅骨分割,其结果要优于数学形态学方法的分割结果。而经有监督描述子学习算法进行特征压缩后取得的分割准确率也要高于特征压缩前的分割准确率,这充分证明了本文分割算法的有效性,并且体现了SVM结合有监督描述子学习算法的优势。另外,由于本文方法依赖于图像的配准技术,需要将病人的MR图像与参考MR进行配准,也需要将病人的CT图像配准到参考CT图像,造成程序存在时效性问题,因此下一步工作可集中于研究高效的配准算法,进一步提高本文算法的时效性。
[1]Potthast R,Kühn L.On the convergence of the finite inte⁃gration technique for the anisotropic boundary value prob⁃lem of magnetic tomography[J].Mathematical methods inthe applied sciences,2003,26(9):739-57.
[2]Cuffin BN.A method for localizing EEG sources in realis⁃tic head models[J].Biomedical Engineering,IEEE Trans⁃actions on,1995,42(1):68-71.
[3]刘金山,陈镇坤,黄来华.基于贝叶斯分层混合模型的大脑FMRI图像分割[J].数理统计与管理,2015,34(4):603-611. LIO Jinshan,CHEN Zhenkun,HUANG Laihua.Sege⁃mentation of Brain FMRI Based on Bayesian Hierarchical Mixture Model[J].Journal of Applied Statistics and Man⁃agement,2015,34(4):603-611.
[4]刘凡,高上凯,高小榕.基于最大后验概率的大脑磁共振图像的三维分割[J].清华大学学报:自然科学版,2002(S1):43-48. LIU Fan,GAO Shangkai,GAO Xiaorong.3-D Segmenta⁃tion of Brain Magnetic Resonance Images Based on Maxi⁃mum a Posterior[J].Journal of Tsinghua University(Sci& Tech),2002(S1):43-48.
[5]Heinonen T,Eskola H,Dastidar P,Laarne P,Malmivuo J.Segmentation of T1 MR scans for reconstruction of resis⁃tive head models[J].Computer methods and programs in biomedicine,1997,54(3):173-81.
[6]Rifai H,Bloch I,Hutchinson S,Wiart J,Garnero L.Seg⁃mentation of the skull in MRI volumes using deformable model and taking the partial volume effect into account[J].Medical image analysis,2000,4(3):219-33.
[7]Chu C,Takaya K,editors.3-dimensional rendering of MR(magnetic resonance)images[C]//WESCANEX 93‘Com⁃munications,Computers and Power in the Modern Envi⁃ronment'Conference Proceedings,IEEE,1993:IEEE.
[8]Dogdas B,Shattuck DW,Leahy RM.Segmentation of skull and scalp in 3-D human MRI using mathematical morphol⁃ogy[J].Human brain mapping,2005,26(4):273-85.
[9]Golub GH,Van Loan CF.Matrix computations[M].JHU Press,2012.
[10]Dhillon IS,Modha DS.Concept decompositions for large sparse text data using clustering[J].Machine learning,2001,42(1-2):143-75.
[11]Srebro N,Jaakkola T,editors.Weighted low-rank ap⁃proximations[M].ICML,2003.
[12]Thomasian A,Castelli V,Li C-S,editors.Clustering and singular value decomposition for approximate index⁃ing in high dimensional spaces[C]//Proceedings of the seventh international conference on Information and knowledge management,1998:ACM.
[13]Achlioptas D,McSherry F.Fast computation of low-rank matrix approximations[J].Journal of the ACM(JACM),2007,54(2):9.
[14]Shi G,Liu D,Gao D,Liu Z,Lin J,Wang L.Advances in theory and application of compressed sensing[J].Acta Electronica Sinica,2009,37(5):1070-81.
[15]Zhen X,Wang Z,Yu M,Li S,editors.Supervised de⁃scriptor learning for multi-output regression[C]//Pro⁃ceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2015.
[16]Ye J.Generalized low rank approximations of matrices[J].Machine Learning,2005,61(1-3):167-91.
[17]Chang C-C,Lin C-J.LIBSVM:a library for support vec⁃tor machines[J].ACM Transactions on Intelligent Sys⁃tems and Technology(TIST),2011,2(3):27.
Automated Segmentation Based on Support Vector Machine and Supervised Descriptor Learning from Brain MR Image
HUANG Yongqi1,2SHI Wenbo3ZHOU Zhiyong1PANG Shumao4TONG Baotong1ZHAO Lingxiao1DAI Yakang1
(1.Suzhou Institute of Biomedical Engineering and Technology of Chinese Academy of Sciences,Suzhou215263)(2.University of Chinese Academy of Sciences,Beijing100049)(3.Beijing Normal University,Beijing100875)(4.Southern Medical University,Guangzhou510515)
A solution of EEG/MEG forward problem is essential and important in stereotactic neurosurgery applications.It is necessary to build a multi-layer brain model to distinguish different tissues for MEG/EEG forward problem.Although soft tissues can be clearly seen in MR images,but the intensity of skull is so low because of a lack of hydrogen in skull that can't be segmented auto⁃matically and accurately from MR image.Extracting skull form MR image automatically end up to be a key problem when calculating the MEG/EEG forward problem.In order to solve the above problem,a support vector machine(SVM)is proposed based segmentation algorithm using global features and local features of MR image.Moreover,the supervised descriptor learning(SDL)algorithm is com⁃bined that can transform the feature matrix into a compact one,and finally the skull from brain MR image is extrated by training on multi-modal images from the same patient whose CTs and MRs are available.Compared to the algorithm based on SVM only and math⁃ematical morphology based algorithm,the proposed method shows a considerable improvement on segmentation accuracy.The pro⁃posed method achieves an accuracy with Dice coefficient 0.832 compared with the other two methods 0.798 and 0.482.The proposed hybrid algorithm extract the skull successfully,so that the EEG,MEG source imaging problem can be solved easily in future work.
kull segmentation,support vector machine(SVM),supervised descriptor learning(SDL),feature extraction,feature compression
TP391
10.3969/j.issn.1672-9722.2017.07.034
2017年1月13日,
2017年2月28日
中国科学院百人计划项目;国家自然科学基金(编号:61301042);国家863计划(编号:2015AA020514);国家自然科学基金青年基金项目(编号:61501452);江苏省博士后基金项目(编号:1501089C)资助。
黄勇其,男,硕士研究生,研究方向:智能医学图像处理。史文博,男,研究方向:图像处理。周志勇,男,博士,研究方向:医学图像处理与分析算法。庞树茂,男,硕士研究生,研究方向:医学图像分析,医学大数据。佟宝同,男,硕士,研究方向:医学图像处理软件开发。赵凌霄,男,博士,研究方向:医学影像分析处理与可视化算法研究和软件开发。戴亚康,男,研究方向:医学图像处理算法研究和软件开发。

