基于蒙特卡洛有限元算法的建筑节约用材研究∗

申琳 李晓刚

（1.杨凌职业技术学院杨凌712100）（2.西安协鑫新能源管理有限公司西安733000）

基于蒙特卡洛有限元算法的建筑节约用材研究∗

申琳1李晓刚2

（1.杨凌职业技术学院杨凌712100）（2.西安协鑫新能源管理有限公司西安733000）

针对建筑用材在现实生活中过度消耗的问题，该研究以建筑结构节约用材为切入点，深入分析结构荷载可靠性指标，通过摄动有限元算法结合随机场效应在计算可靠性指标的基础上，构建了解决建筑节约用料的蒙特卡洛有限元算法。利用Hasofer迭代和Orthogonal变换分别优化功能函数和随机变量转换，将标准正态变量空间与中心原点距离最小值的点作为算法的核心，给出了节约条件下建筑用材的结构可靠性求解。通过建筑过程中的梁可靠度进行分析，结果表明：该研究提出的算法在随机参数较小的条件下，建筑结构强度仍具有可靠性，对减少建筑用材的需求具有参考性。

有限元算法；蒙特卡洛方法；建筑用料；结构可靠性；节约用材

Class NumberTP391.7

1 引言

随着计算机技术的迅速发展，建筑节约用材及其带动的数据分析量在不断扩大。建筑材料是建筑业建设的物质基础保障，并且众多的原材料作为不可再生资源令我国耗材巨大。为了解决建筑节能设计，利用计算机技术与软件信息对建筑设计起到了至关重要的辅助功能［1］。目前常用的建筑辅助软件有建筑信息模型（BIM）［2］、计算机辅助建筑设计（CAAD）［3］和谷歌草图大师（Google Sketchup）［4］等。同时，计算机技术处理建筑节约用材主要运用了DTAC算法［5］、遗传算法［6］和粒子群算法［7］等。本研究以有限元算法为主线，利用建筑结构势能泛函数、极限状态分别分析了结构随机参数、结构可靠性，将随机场加入到模型中，结合摄动随机有限元法和可靠指标共同建立蒙特卡洛有限元优化迭代算法求解建筑节约用材可靠指标。该算法重点分析了建筑节约用材后的可靠性，为集约化建筑用料提供改了计算参考意义。

2 蒙特卡洛有限元算法

2.1 摄动随机有限元法

利用建立在随机场的S(x，θ)，对满负结构荷载以及充满弹性参数的模量进行处理［8］，并通过采用空间离散的方法，对随机场S(x，θ)内的随机变量S=[S1，S2，…，SM]T实行转化。利用变分法［9］，同时在构建结构势能泛函数的开始就将结构随机参数以随机性的方式加入到模型之中，从而来构建随机有限元法控制方程，构建的方程如下：

在上述方程中，K-，a-和P-分别表示随机矩阵K，a和P在均值S-处的值，Ki，ai和Pi分别表示K，a和P对Si的一阶偏导数在S-处之值。

2.2 结构可靠性

对结构的可靠性进行分析的过程中，我们能够利用功能函数Z对结构的极限状态进行描述［10］，这样的情况下将会影响自变量，当结构工作中的基础随机变量成为自变量，Z可写为

在上述的函数中，S表示在建筑结构中施工过程以及使用材料的过程中几何参数、材料参数以及荷载参数等变量。关于建筑过程中的结构可将其定义为［11］

在上述的公式中，σz以及Z-分别表示功能函数Z的标准差和均值。

2.3 优化迭代算法

从优化迭代算法的角度来看，可以从几何意义的角度出发来对结构可靠的指标进行求解。在标准的正态随机变量空间中，随机变量的几何意义代表着极限状态曲面到坐标原点之间距离的最小值。因此，在标准的正态随机变量空间中［12］，获得可靠指标的途径，需要通过在功能函数面G(x)上找到与坐标原点之间距离最小值的点P*。而实际上，对于寻找的点P*是一个优化的问题：

在上述的公式中，x*=(x1*，x*2，…，x*n)代表着功能函数Z面上的随机验算点。通过Hasofer的优化迭代算法进行采用后［13］，还需要对式（4）进行求解。通过式（5）的方法，能够得出验算点x*的位置：

如上所示，x(k+1)表示第k+1次的优化迭代算法而计算得到的验算点，‖gradG(x(k))‖和gradG(x(k))则分别代表着由第k次优化迭加而计算出的功能函数的范数以及梯度，而ξ则表明了迭代中验算点移动的总体方向。

3 建筑节约用材可靠性指标

3.1 梯度函数求解

人们常用的RMCS方式主要是通过分析抽样的方法来对一些可靠的指标数据进行获取［14］，而本文选取的优化迭代算法是建立在摄动随机有限元法求解的方法上对可靠指标进行获取。本文选取的优化迭代算法之所以能够实现与摄动随机有限元法相结合，其最为关键的原因在于，根据前部分提出的式（5），在得知随机有限元法控制方程的情况下很容易推算出式子中的梯度向量gradG(x(k))。一般情况下得到的信息仅仅限于一些仅能够表现出变量结构的随机变量S，而实际上并不能通过在非标准的空间下对处于非正态分布的随机变量空间的随机变量进行推算，因此能够得出gradG(x(k))为

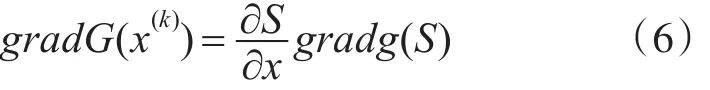
对于一般难以用随机变量进行表达的功能函数g(S)，无法直接通过推理和计算的方式来对梯度gradg(S)进行求解。而在我们研究的对象转为力学的时候，在力学特性的基础上将可以对功能函数进行划分，将其中的随机变量划分为结构抗力R以及随机变量S等两类与作用效应F有关类别。根据上述的描述，可以得到如下的功能函数的梯度为

式（7）中，gR，gF代表中间变量R，F的梯度向量，JR，JF分别表示R，F的Jacobi矩阵。对于无法解决S显式表示的结构随机响应F，我们能够利用Jacobi矩阵来进行求解，但是在整体过程中，求解JF的过程非常繁杂。相对来说gF以及JR，gR都是比较容易求解得出的。这帮助了我们来确定下一步，即需要确定JF的第i行的转置是随机响应F的一阶偏导数，因此取结点位移为{ai}时能够得到下式

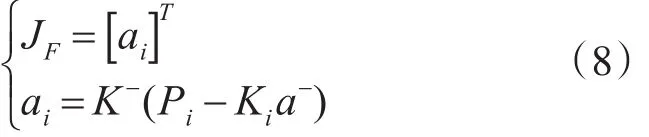
3.2 变量变换

对于一阶偏导数∂S/∂x的确定，首先需要确定的就是随机变量S如何进行处理的问题，首先将采取Orthogonal的变换［15］，在利用正交变换的方法得出非相关随机变量Y：

上式中的A是通过正交规范化特征向量形成的矩阵，再将Y进行标准化处理，得出非相关性的标准正态随机变量X：

上式中，Y-i，σYi代表着Yi的均值和标准差。

3.3 算法求解流程

将优化迭代算法以及摄动随机有限元法的方法相结合，计算出标准正态变量空间与中心原点距离最小值的点，这种基于验算点的迭代算法记为RPSFEM1。其具体的步骤如下：

Step1：首先需要将随机场进行离散处理，离散成为随机变量S，同时计算出S的协方差矩阵CS，此时还需要计算出CS的特征向量和特征值；

Step2：参照功能函数式F分别求出一阶导数∂g/∂R和∂g/∂F；

Step3：将初始的迭代点设定为S(0)，一般情况下一般将均值点S-设立为初始迭代点，此时，β0=0；

Step4：在优化迭代算法开始时，再形成刚度矩阵S-以及荷载列阵P-，解刚度方程得a-，形成验算点处的Ki，Pi，由式（1）求得ai；

Step5：通过计算建筑材料结构控制面挠度σ求解变量结构的随机变量Si的一阶偏导数，利用式（6）、（7）和（10）计算功能函数梯度的gradG(S)；

Step6：最后通过计算功能函数g(S)对迭代效果进行算法收敛判断，若g(S)≤ε，则对寻找的点可靠性指标继续进行判别：如Δβ＞ε，则算法转至Step3，继续进行迭代计算；若Δβ≤ε，则算法满足收敛条件，停止迭代。

从上述的优化迭代算法的基本步骤中看到，在Step4时，当变异系数处于较低值的时候，能够计算出验算点位移的大小。还可以计算出在均值处a，ai，aij位移发生后，再利用a*i=Si*-Si-的公式来求出位移a*。这种基于均值点的迭代算法记为RPSFEM2。

4 实验模拟

在实验模拟的部分将分三种情况来考虑设定的随机参数的随机性。首先是对弹性模量进行的随机性考察，在处理中将均布荷载当作已经确定的参数；再者需要对均布荷载的随机性进行考察；最后还需要将前两者的情况同时考察。在这三种不同的建筑情况下，可以分别利用RPSFEM1和RPS⁃FEM2对建筑过程中的梁可靠度进行分析，同时还需要将这些结果进行比较并且做出误差分析，分析如图1～图3所示。

图1建筑材料弹性模量随机性

图2建筑材料均布荷载随机性

图3建筑材料弹性模量和均布荷载随机性

从图1中不难发现，在弹性模量设定随机的情况下，在变异系数低于0.10的情况下，采用RPS⁃FEM1以及RPSFEM2得出的演算结果未呈现出明显的差异，同时通过RMCS的计算以及前者的计算均低于5%。在变异系数高于0.10时，与RPS⁃FEM1，RPSFEM2的计算方法相比，得出的结果与之前的计算方法得出的计算结果相对误差较小。当随机系数开始变大的时候，RPSFEM1以及RPS⁃FEM2得出的演算结果的误差也在相应的增加，并且当变异系数高于0.10时，两者之间的误差较大，而在变异系数为0.15时，误差高达7%。

从图2中不难发现，当处于荷载随机的状态下，当得出的变异系数在逐步增加时，采用RPS⁃FEM1以及RPSFEM2得出的演算结果未呈现出明显的差异。还发现，尽管采用RPSFEM1、RPSFEM2与RMCS方法得出的误差和变异系数的增加呈现正相关，但是这样的误差并不超过1%。

从图3中不难发现，在两者同时随机的情况下，当得出的变异系数在逐步增加时，采用RPS⁃FEM1以及RPSFEM2得出的演算结果未呈现出明显的差异。但是与前者不同的在于，随着变异系数的增大，它们的误差也会增大。当计算出的变异系数低于0.10时，采用前者计算方法得出的结果与后者得出的计算结果误差小于5%。当计算出的变异系数等于0.10时，采用前者计算方法得出的结果与后者得出的计算结果误差都比较大。当计算出的变异系数高于0.10时，采用前者计算方法得出的结果与后者得出的计算结果误差高达6.6%。通过对比，能够得出的结论是，在荷载随机影响的情况下，利用RPSFEM1和RPSFEM2得出的计算结果是吻合得相对较好的。通过将第一种情况与第三种情况相对比我们也不能发现，在弹性模量的随机影响下，当变异系数高于0.15时，采用前者计算方法得出的结果与后者得出的计算结果误差相对较高，高于5%，因此只能应用于随机参数较小的可靠度分析。

5 结语

本文以建筑结构可靠性为出发点，重点分析了外荷载随机性条件下的建筑材料弹性模量，旨在减少建筑用料。利用摄动有限元算法结合随机场效应在计算可靠性指标，构建了蒙特卡洛有限元算法的结构可靠性求解，分别利用Hasofer迭代和Or⁃thogonal变换优化了算法的求解，并且通过建立基于验算点和均值点的迭代算法给出了节约条件下建筑用材的结构可靠性。最后通过对建筑材料弹性模量的演算结果表明：利用细化后的两种算法方式可为建筑节约用材条件下的可靠性进行计算，这为减少建筑用材提供了数据计算保证。

［1］王鹏飞.浅谈计算机辅助建筑设计与绿色建筑设计的结合［J］.计算机光盘软件与应用，2013（7）：40-41. WANG Pengfei.Discussion on the Combination of Comput⁃er Aided Architectural Design and Green Building Design［J］.Computer CD-ROM Software and Application，2013（7）：40-41.

［2］周春波.BIM技术在建筑施工中的应用研究［J］.青岛理工大学学报，2013，34（1）：51-54. ZHOU Chunbo.Application of BIM Technology in Build⁃ing Construction［J］.Journal of Qingdao Technological University，2013，34（1）：51-54.

［3］孙晓峰，魏力恺，季宏.从CAAD沿革看BIM与参数化设计［J］.建筑学报，2014（8）：41-45. SUN Xiaofeng，WEI Likai，JI Hong.Evolution of CAAD from BIM and Parametric Design［J］.Journal of Architec⁃tural Education，2014（8）：41-45.

［4］张瑞菊.SketchUp结合Google Earth在虚拟校园中的应用［J］.计算机应用，2013，33（1）：271-272. ZHANG Ruiju.The Application of SketchUp in Virtual Campus［J］.Computer Application，2013，33（1）：271-272.

［5］黄志炜，骆世广，李绵升.动态目标的建筑供冷自适应控制机制研究［J］.建筑节能，2013（5）：8-11. HUANG Zhiwei，LUO Shiguang，LI Jinsheng.Research on Adaptive Cooling Mechanism of Buildings with Dynamic Targets［J］.Building Energy Efficiency，2013（5）：8-11.

［6］谌文武，张宇翔，和法国.基于FLAC和遗传算法的斜坡加固方案优化方法［J］.中南大学学报（自然科学版），2011，42（11）：3507-3514. KAN Wenwu，ZHANG Yuxiang，HE Faguo.Optimization of Slope Reinforcement Schemes Based on FLAC and Ge⁃netic Algorithm［J］.Journal of Central South University（Natural Science），2011，42（11）：3507-3514.

［7］吴洲，叶倩，罗堃.基于粒子群算法的室内环境节能优化控制［J］.微计算机信息，2010，26（7）：159-161. WU Zhou，YE Qian，LUO Kan.Energy-saving optimiza⁃tion control of indoor environment based on particle swarm optimization［J］.Microcomputer information，2010，26（7）：159-161.

［8］张传岩，洪晓光，彭朝晖.基于SVM和扩展条件随机场的Web实体活动抽取［J］.软件学报，2012，23（10）：2612-2627. ZHANG Chuanyan，HONG Xiaoguang，PENG Chaohui. Extraction of Web Entities Based on SVM and Extended Conditional Random Fields［J］.Journal of Software，2012，23（10）：2612-2627.

［9］丁光涛.变分法逆问题研究的若干进展［J］.北京大学学报（自然科学版），2016，52（4）：732-740. DING Guangtao.Some Advances in Inverse Problem of Variational Method［J］.Journal of Peking University（Nat⁃ural Science），2016，52（4）：732-740.

［10］冯兴中.工程结构承载力极限状态与正常使用极限状态可靠度的比较分析［J］.西北水电，2011（2）：66-71. FENG Xingzhong.Comparison and Analysis of Bearing Capacity Limit State and Normal Service Limit State Reli⁃ability of Engineering Structures［J］.Northwest Hydro⁃power，2011（2）：66-71.

［11］刘国承，秦训鹏，魏青松.单轴压缩金属粉末材料屈服准则研究［J］.华中科技大学学报（自然科学版），2016，44（7）：96-99. LIU Guocheng，QIN Xunpeng，WEI Qingsong.Study on Yield Criterion of Uniaxial Compression Metal Powder［J］.Journal of Huazhong University of Science and Tech⁃nology（Nature Science），2016，44（7）：96-99.

［12］杨绿峰，杨显峰，余波.基于Nataf变换的层递响应面法分析结构可靠度［J］.计算力学学报，2014（2）：155-160. YANG Lvfeng，YANG Xianfeng，YU Bo.Analysis of Structural Reliability by Layered Response Surface Meth⁃od Based on Nataf Transform［J］.Chinese Journal of Computational Mechanics，2014（2）：155-160.

［13］毛力奋.考虑可靠性和鲁棒性的机械接头有限元设计优化［J］.计算机辅助工程，2010，19（3）：101-105. MAO Lifen.Optimization of Mechanical Joint Finite Ele⁃ment Design Considering Reliability and Robustness［J］. Computer Aided Engineering，2010，19（3）：101-105.

［14］练秋生，肖莹.基于小波树结构和迭代收缩的图像压缩感知算法研究［J］.电子与信息学报，2011，33（4）：967-971. LIAN Qiusheng，XIAO Ying.Research on Image Com⁃pression Sensing Algorithm Based on Wavelet Tree Struc⁃ture and Iterative Shrinkage［J］.Electronics and Infor⁃matics，2011，33（4）：967-971.

［15］吴迪，王奎民，赵玉新.分段正则化正交匹配追踪算法［J］.光学精密工程，2014，22（5）：1395-1402. WU Di，WANG Kuimin，ZHAO Yuxin.Piecewise Regu⁃larized Orthogonal Matching Pursuit［J］.Optics and Pre⁃cision Engineering，2014，22（5）：1395-1402.

Building Material Saving Based on Monte Carlo Finite Element Method

SHEN Lin1LI Xiaogang2
（1.Yangling Vocational&Technical College，Yangling712100）（2.Xi'anXiexinNewEnergyManagementCo.，Ltd，Xi'an733000）

In order to solve the problem of excessive consumption of building materials in real life，this paper takes the build⁃ing material saving material as the starting point，analyzes the structural load reliability index，and calculates the reliability index by the perturbation finite element method combined with the random field effect.The Monte Carlo finite element method for solving the problem of building material saving is constructed.By using the Hasofer iteration and the Orthogonal transformation，the func⁃tion function and the random variable transformation are optimized respectively.The point where the standard normal variable space and the central origin distance are minimum is taken as the core of the algorithm.The structural reliability of the building material is saved under the saving condition.The results show that the proposed algorithm is reliable in the case of small stochastic parameters and can be used as a reference for reducing the demand of building materials in the construction process.

finite element method，Monte Carlo method，building materials，structural reliability，material saving

TP391.7

10.3969/j.issn.1672-9722.2017.07.006

2017年1月7日，

2017年2月11日

申琳，女，硕士，讲师，研究方向：建筑结构。李晓刚，男，工程师，研究方向：工程管理。