时滞依赖状态的半线性微分包含的可控性分析∗

李文胜 杨陈东

（西安航空学院理学院西安710077）

时滞依赖状态的半线性微分包含的可控性分析∗

李文胜 杨陈东

（西安航空学院理学院西安710077）

利用Dhage多值映射不动点定理结合算子半群理论，在公理化定义的相空间上，研究一类非局部初始条件下时滞依赖状态的半线性微分包含的可控性。

时滞依赖状态；算子半群；微分包含

Class NumberO175.22

1 引言

近年来，微分包含理论已得到广泛关注和应用，因此这些系统受到越来越多的研究，各种结果相继建立［1～6］。

本文主要考虑一类时滞依赖状态的半线性微分包含：

其中A是Banach空间(X，‖·‖)中强连续半群(T(t))t≥0的无穷小生成元；L2(J，U)是容许控制函数构成的Banach空间，控制函数u(·)在L2(J，U)中取值，U是一个Banach空间；P(X)是X的所有非空子集类；F:J×B→P(X)是有界闭凸值多值映射，g:C(J，X)→X是给定的函数；B是一个抽象的相空间；xt:(-∞，0]→X，属于抽象的相空间B， xt(s)=x(t+s)，s≤0。

2 预备知识

L(X)是从X到X的有界线性算子构成的Banach空间。一个可测函数x:J→X是Bochner可积当且仅当‖x‖是Lebesgue可积，更多有关Bochner积分的性质参见文献［7］。L1(J，X)是Bochner可积的连续函数x:J→X组成的Banach空间，赋予范数

有关公理化定义的相空间B，可参见文献［8］。

引理1［9］若集值映射F有非空紧值且全连续，则F是上半连续的当且仅当F有闭图像（即当xn→x*，yn→y*，yn∈F(xn)时，有y*∈F(x*)。

定义1称F:Rτ×B→P(X)为Caratheodory集值映射，假如

1）对每个ψ∈B，t→F(t，ψ)是可测的；

2）对任意的t∈Rτ，ψ→F(t，ψ)为上半连续的。

引理2［9］若F为Caratheodory多值映射，且对给定的ψ∈B，集合SF，ψ={∈L1(Rτ，X):f(t)∈fF(t，ψ)，t∈Rτ}是非空的，Γ:L1(Rτ，X)→C(Rτ，X)为线性连续映射，则Γ°SF:C(Rτ，X)→Pcp，cv(C(Rτ，X))，y→(Γ°SF)(y)=Γ(SF，y)是C(Rτ，X)× C(Rτ，X)上的闭图算子。

定义2函数x:(-∞，a]→X称为问题（1）～（2）的温和解，如果对任意的s∈J，有x0=φ，xρ(s，y)∈B，并且满足：

s

引理3［10］如果多值映射Γ1:X→Pbd，cl，cv(X)和Γ2:X→Pcp，cv(X)满足：

1）Γ1是压缩的；

2）Γ2是全连续的；

那么

1）当λ=1时，算子包含λx∈Γ1x+Γ2x有一个解，或者

2）集合{u∈λΑ1u+λΓ2u，0＜λ＜1}是无界的。

3 主要结果

为了讨论问题（1）～（2）的可控性，假定以下条件成立：

H1.函数t→φt从R(ρ-)={ρ(s，ψ):ρ(s，ψ)≤0，(s，ψ)∈J×B}到B上是连续的，且存在一个连续有界函数Jφ:R(ρ-)→(0，∞)，使得对每个t∈R(ρ-)，有‖φt‖B≤Jϕ(t)‖φ‖B。

H2.线性算子W:L2(J，U)→X定义为Wu=T(b-s) Bu(s) ds，W有一个在L2(J，U)/kerW中取值的诱导逆算子，并且存在正常数M1，M2，使得

H3.T(t)是紧算子，且存在一个常数M＞0，使得当t∈J时，‖T(t)‖≤M。

H4（1）F:J×B→Pbd，cp，cv(X)，对每个ψ∈B，t→F(t，ψ)是可测的；对任意的t∈J，ψ→F(t，ψ)是上半连续的；对固定的ψ∈B，集合SF，ψ= {f∈L1(J，X):f(t)∈F(t，ψ)a.e.t∈J}是非空的。

H4（2）存在一个可积函数m:J→[0，+∞)和一个连续非减函数W:[0，∞)→(0，∞)，使得‖F(t，ψ)‖=sup{‖f‖:f(t)∈F(t，ψ)}≤m(t) W(‖ψ‖B)，(t，ψ)∈J×B。

H4（3）Hd(F(t，ψ1)-F(t，ψ2))≤MF‖ψ1-ψ2‖B，(t，ψ)∈J×B。

备注1［11］设φ∈B且t≤0。φt为定义成φt(θ)=φ(t+θ)形式的泛函。由此可知，如果泛函x(·)使得x0=φ，则有xt=φt。

备注2令Ma=supt∈JM(t)，Ka=maxt∈JK(t)，且M*=Mmax{eωa，1}。

定理1假设H1～H4成立，如果

则系统（1）～（2）在J上是可控的。

证明：利用假设H2，对任意的x()·，可定义控制：

ux(t)=W-1{x1-T(b)[φ(0)-g(x)]-T(b-s) f(s) ds}(t)其中SF，xˉρ={f∈L1(J，X):f(t)∈F(t，xˉρ(t，xt))，a.e.t∈J}，xˉ:(-∞，a]→X满足xˉ0=φ，且在J上xˉ=x。

令Br={x∈X:‖x‖PC≤r}，对任意的r＞0，易知Br是X中的一个有界闭凸子集。

考虑空间Bˉ0a={z∈Bˉa:z0=0}。记‖·‖a是Bˉ0a的半范数且定义为

显然(Bˉ0a，‖·‖a)是一个Banach空间。

考虑如下算子：Γ:Ba→P(Ba)

0

0

将Γ分解为Γ=Γ1+Γ2，其中

为了应用引理3，将证明分为如下几步：

第一步，Γ1是在Br上是压缩的。

因此

第二步，Γ2是全连续算子：

1）易知Γ2(Br)是有界的。

2）Γ2(Br)是等度连续的。

假如t1，t2∈J，t1＜t2。设z∈Br，ℜ1∈Γ2(z)，则存在f∈SF，zρ，使得

则

其中r**=(Ma+Jφ+MHKa)‖φ‖B+Kar。

（3）使用OPC-UA：OPC-UA传递的数据是可加密的，并对通信连接和数据本身都可实现安全控制。这种新的安全变种可以保证从原始设备到MES、ERP系统的各种数据的可靠传递。

因为T(t)是强连续的并且T(t)，(t＞0)是紧的，所以T(t)，(t＞0)是一致算子拓扑连续的。又因t2→t1且ε充分小，所以上述不等式的右边趋于零并且与x∈Br无关。因此Γ2把有界集映成等度连续集。

3）对每个t∈J，(Γ2Br)(t)={ℜˉ1(t):ℜˉ1∈Γ2(Br)，t∈J}是相对紧的。

当t=0时，显然Γ2(Br)(t)在X中是相对紧的。假如0＜t≤a是固定的且0＜ε＜t，对任意的z∈Br和ℜˉ1∈Γ2(y)，存在f∈SF，xˉ，使得

ρ

由算子T(ε)的紧性可知

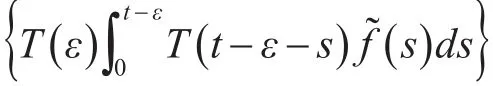
因为

不等式右端当ε→0时，一致收敛于零。存在相对紧集序列无限逼近于集合所以集合是X中的相对紧集。

类似于文献［3］，Γ2是全连续多值映射，根据Arzela-Ascoli定理可以得出Γ2是全连续多值映射。由引理3知，微分包含问题（1）～（2）是可控的。

4 结语

利用集值映射不动点定理结合算子半群理论，在微分包含有关理论及给定条件的基础上，先将系统转化成积分方程，然后按照给定的不动点定理，逐步证明了时滞依赖状态的半线性微分包含的可控性。此分析方法对同类系统可控性的研究具有促进意义。

［1］Vijayakumar V，Ravichandran C，Murugesu R，et al.Con⁃trollability results for a class of fractional semilinear inte⁃gro-differential inclusions via resolvent operators［J］.Ap⁃plied Mathematics and Computation，2014，247（15）：152-161.

［2］Sotiris K.Ntouyas，Sina Etemad.On the existence of solu⁃tions for fractional differential inclusions with sum and in⁃tegral boundary conditions［J］.Applied Mathematics and Computation，2015，266（1）：235-243.

［3］Li W-S，Chang Y-K，Nieto J.J.Solvability of impulsive neutral evolution differential inclusions with state-depen⁃dent delay［J］.Math.Comput.Modelling，2009，49（9-10）：1920-1927.

［4］Chang Y K，Nieto J J，Li W S.Controllability of Semilinear Differential Systems with Nonlocal Initial Conditions in Banach Spaces［J］.Journal of Optimization Theory and Ap⁃plications，2009，142（2）：267-273.

［5］Bashir Ahmad，Sotiris K.Ntouyas，Jessada Tariboon.A study of mixed Hadamard and Riemann-Liouville fraction⁃al integro-differential inclusions via endpoint theory［J］. Applied Mathematics Letters，2016，52：9-14.

［6］李文胜，周千，韩慧蓉.随机脉冲随机偏发展微分包含解的存在性［J］.应用数学学报，2015，38（6）：1059-1073. LI Wensheng，ZHOU Qian，HAN Huirong.Existence re⁃sults for a stochastic partial evolution differential inclu⁃sions with random impulses［J］.Acta Mathematicae Appli⁃catae Sinica，2015，38（6）：1059-1073.

［7］Yosida K.Functional Analysis［M］.6th ed.Berlin：Spring⁃er-Verlag，1980.

［8］Hernández E，Prokopczyk A，Ladeira L.A note on partial functional differential equations with state-dependent de⁃lay［J］.Nonlinear Anal RWA，2006，7（4）：510-519.

［9］Lasota A，Opial Z.An application of the Kakutani-Ky Fan theorem in the theory of ordinary differential equations［J］.Bulletin de I'Academie Polonaise des Sciences，Se⁃rie des Sciences.Mathematiques，Astronomiques et Phy⁃siques，1965 13：781-786.

［10］B.C.Dhage.Fixed-point theorems for discontinuous multi-valued operators on ordered spaces with applica⁃tions［J］.Comput.Math.Appl，2006，51（3-4）：589-604.

［11］Hernández E.Existence results for partial neutral integro⁃differential equations with unbounded delay［J］.J Math Anal Appl，2004，292（1）：194-210.

Controllability for Semilinear Differential Inclusions with State-dependent Delay

LI WenshengYANG Chendong
（Faculty of Science，Xi'an Aeronautical University，Xi'an710077）

In this paper，a sufficient condition for the controllability of a semilinear differential inclusions is established with state-dependent delay.The approach used is the Dhage multi-valued fixed-point theorem combined with operator semigroups.

state-dependent delay，operator semigroups，differential inclusions

O175.22

10.3969/j.issn.1672-9722.2017.07.002

2017年1月9日，

2017年2月13日

国家自然科学基金（编号：11161027）；陕西省教育厅科研项目（编号：15JK1379）；西安航空学院科研基金

（编号：2014KY1210）资助。

李文胜，男，硕士，讲师，研究方向：算子理论。杨陈东，男，硕士，研究方向：计算机科学与技术。