用于无人机精确着舰的翼伞归航控制方法

王帝 滕海山 吴世通

（北京空间机电研究所，北京 100094）

用于无人机精确着舰的翼伞归航控制方法

王帝 滕海山 吴世通

（北京空间机电研究所，北京 100094）

舰载无人机是未来的发展趋势，无人机如何能够精确安全着陆在小型舰船是亟需解决的关键技术。文章介绍了一种采用可控翼伞实现无人机精确着舰的回收方法，在传统的翼伞分段式归航控制方法的基础上，设计了一种带末段修正的改进型归航控制方法，有效提高了翼伞归航精度；再结合受控动目标协作控制方法，实现翼伞载无人机的精确着舰。文章建立了归航控制航迹规划模型，通过MATLAB软件进行了仿真分析，验证了控制方法的可行性，并与传统的分段归航控制方法进行比较，证明了该方法可显著提高着陆精度。

翼伞 无人机 分段归航 动目标 航迹规划 着舰回收

0 引言

自从20世纪80年代末，美国海军率先将无人机搬上“依阿华号”战列舰，用于侦察、目标指示、校正弹道等作战任务[1-2]。在1991年的海湾战争中，“威斯康星号”和“密苏里号”战列舰凭借舰载无人机的杰出性能，给伊军以沉重打击。随着无人机技术的飞速发展，在不久的将来，舰载无人机必将成为水面舰艇的重要装备。在无人机执行任务过程中，回收过程是一个非常重要且容易出现故障的阶段。有资料表明，无人机回收过程的故障数占无人机整个执行任务故障数的 80%以上[3]。因此，对舰载无人机回收的研究非常必要。

目前，舰载无人机的回收方式可归纳为轮式着陆、撞网回收、伞降回收、天钩回收、绳钩回收等类型，其中轮式着陆、撞网回收和伞降回收是比较常用的回收方式。轮式着陆有丰富的可用经验，但是需要较大甲板；撞网回收无需较大甲板，但是需要在尾部展开拦截网；普通伞降回收较为平稳，但是落点位置精度较低，难以安全准确地降落在舰船甲板上，多采用在水面上降落，落水后会对无人机及其内部设备造成不良影响。如果能够有效地提高伞降回收的落点精度，该回收方式将成为舰载无人机精确着舰的主要方法。由此可见，无人机如何精确安全着陆在小型舰船上是目前需要解决的关键问题[2-3]。

近年来提出了采用翼伞实现无人机精确回收的方法，该方法可以有效降低无人机的着陆速度，提高着落精度，使无人机安全降落在舰船上。美国海军某研制团队从2009年起，使用高性能翼伞和GPS定位系统，携带负载，将落点精度从最初的100m逐步减小到25m，并计划误差达到10～15m范围内后投入使用[4-6]。

传统的翼伞分段归航方式一般分为飞向目标、盘旋削高、逆风对准、雀降着陆这几个阶段[7-10]。这种归航方式，在盘旋削高段绕目标点盘旋，当高度低于某一数值时，进入逆风对准阶段，并开始寻找逆风方向，准备雀降，即从逆风对准阶段起，便不再瞄准目标点的位置，所以该方法很难达到较高的着陆精度。

本文提出一种用于舰载伞翼无人机的落舰控制方法，在传统分段归航的基础上进行了改进，将盘旋削高的盘旋圆设定为切向盘旋，并增加了末段修正环节。另外，针对风浪对舰船和风对翼伞系统的影响，提出采用可控合作动目标的控制方法，实现翼伞带无人机的精确着舰。

1 无人机—翼伞归航控制方案设计

无人机着落于普通的舰船需要解决三方面的问题：一是着舰需要定点着陆精度控制在10m以下的量级，这对于翼伞控制系统是一个重大的技术挑战；二是舰船在海洋上，受到风浪的影响，其水平和垂直位置都会发生随机变化[7]，着陆点成为一个移动的目标，精确追踪困难；三是风对翼伞系统的影响，由于翼伞降低了无人机的飞行速度，使得其飞行速度与风速成为同一个量级（10～20m/s），大大增加了控制的难度。

为实现翼伞无人机系统的精确着舰，需要综合考虑无人机、舰船的位置和运动情况，并综合考虑气象环境的影响。无人机—翼伞飞行分为以下5个阶段，着舰过程如图1所示。

1）无人机根据舰船位置信息和风场信息确定开伞区域；

2）无人机飞到开伞区域范围内，完成翼伞开伞并达到系统稳定；

3）无人机根据舰船位置信息和气象风场信息，确定归航控制方案；

4）翼伞—无人机按设定程序飞行，期间与舰船实时通讯运动信息交互，舰船接收无人机飞行信息及实时落点变化情况，并实时向预报落点靠近；

5）最后阶段，舰船运动方向与翼伞—无人机系统运动同向，两者速度尽量接近。着陆前，翼伞后缘双拉降低垂直速度，无人机着舰。

本文主要针对无人机开伞稳定之后至最终降落到舰船上（即上述的3～5阶段）过程进行方案设计和仿真分析。

2 静目标归航方案

首先考虑将舰船视为一个静止的目标点，在这种情况下实现高精度归航后，在此基础上将静止目标参数化为动目标，模拟在舰船上着陆。

参考传统分段归航的分段方法，将归航着陆过程分为四个阶段：归航接近段、盘旋削高段、盘旋调整段和着舰段。航迹规划的俯视图如图2所示。

航迹规划的过程：

1）归航接近段。翼伞从开伞稳定点A径向归航至P1点上方，经过计算得到轨迹至P2点上方，再到P3点上方进入下一阶段，分别为图2中的I、II、III阶段。

2）盘旋削高段。翼伞从第一次到达 P3点竖直上方开始，以固定单边下拉量盘旋削高，反复进行，且每次经过P3点竖直上方记录高度，当翼伞某次盘旋到达 P3点竖直上方的高度低于某一设定高度时，进入下一阶段，即为图2中的IV阶段。

3）盘旋调整段。当翼伞某次到达 P3点竖直上方的高度低于某一设定高度时，进入盘旋调整段，该阶段是为了末段能够达到合适的飞出高度，根据滑翔比得出该段所需半径，再盘旋至P3点时进入下一阶段，该阶段为图2中的V阶段。

4）着舰段。当翼伞最后一次过P3点时沿此时盘旋圆切线飞出，采用径向归航方式飞向最终目标点，该阶段为图2中的VI阶段。

此过程中假定翼伞的滑翔比恒定为 λ= L/ z （式中，L为翼伞水平方向移动距离；z为竖直方向降落高度），舰船上的最终目标点坐标为(0,0,0)，着舰段飞出点P3的高度为h0，P3点坐标为 (λ h0,0,h0)，根据开伞稳定点A (x0,y0,z0)的位置，选定P1点坐标 (x1, y1,0)，计算得到P2点坐标。

下面对各阶段的飞行航迹进行建模分析。

2.1 归航接近段

翼伞由开伞稳定点 A (x0,y0,z0)至 P1(x1, y1,0)点上方采用径向归航方法，如图3所示。图中，B(x, y, z)为翼伞的位置坐标； ve为当前对地速度在水平面上的分量； vx和 vy为 ve在水平面上在x轴和y轴上的两个分量；ε为速度方向与P1点方向在水平面上的夹角。

该过程采用比例控制，对于在B点处所需的下拉量具体计算公式如下：

式中 lΔ为单边下拉量；maxlΔ 为单边最大下拉量；x1和y1取自P1点坐标。

当翼伞位置坐标(x,y,z)与P1点的水平方向距离小于某定值0σ，视作到达该P1点，并重新记录该点为P1点的坐标以便后续计算的准确性

当翼伞进入到P1点范围内时，视作进入II阶段，该阶段由P1过渡到P2点，采用固定单边下拉量的方式，即首先对P1点的速度方向作出判断，相继求出至P2点所需圆弧的半径，并确定P2点水平坐标。此段目的是要修正翼伞的速度方向及位置，使其更容易在到达P3点时的速度方向与风向相反。调整半径示意见图4。图中，r为从P1点到P2点所需的转弯半径；r0为从P2点到P3点所需的转弯半径。

求解r和r0的具体计算公式如下：

式中 σ是ve与x轴方向的夹角；0hλ 取自P3(x3,y3,z3)点坐标。

解得：

通过所求出的r0，进一步可求出P2点在水平方向的坐标P2(λ h0+ r0, r0,0)。

对于所用模型的转弯半径与单边下拉量的关系如表1所示。

表1 转弯半径与单边下拉量比例的关系Tab.1 The relationship between the radius of turning circle and elongation

转弯半径的倒数与单边下拉量近似成正比关系：

根据表1拟合出的对应关系，代入由式（4）所求出的r，并由此求出此段所需下拉量 lΔ。

同理，当翼伞的位置坐标(,,)x y z与P2点的水平方向距离小于某定值0ε，视作到达该P2点，并重新记录该点为P2点的坐标以便后续计算的准确性。

当翼伞进入到P2点范围内时，视作进入III阶段，该阶段是由第二个过渡点P2到第三个过渡点P3点，因为在P2点速度为垂直于风速，P3点的速度需要与风速反向，需转过90°，依然采用固定下拉量的方式使翼伞轨迹为一个1/4圆弧，由式（4）所求出的r0即为该过程的转弯半径。根据半径与下拉量的对应关系可以求出该段的单边下拉量。

在当翼伞的位置坐标(,,)x y z与P3点的水平方向距离小于某定值0ε，视作到达该P3点，并重新记录该点为P3点的坐标以便后续计算的准确性。

2.2 盘旋削高段

当翼伞到达 P3点时，视作进入盘旋削高段，该阶段是在P3点处切向盘旋削高，以某固定单边下拉量 Δl0使翼伞在每次到达P3点的速度方向都一致，即翼伞速度与风向相反，为了提高最后落点的准确性，每次到达 P3点范围内时，需重新计算与初始P3点在位置上的差距，并对 Δl0做修正。比如到达范围内的点在预定轨迹圆外时，需增加 Δl0，反之减小。

2.3 盘旋调整段

在盘旋削高段，每次翼伞到达 P3点范围内时，需记录当前高度，并对该高度进行检测，若高度已降到 h ≤ k ×h0（k为盘旋调整系数，为一设定常数），则盘旋调整段（见图5）为翼伞在P3点处绕行的最后一圈，并在再次到达P3点时速度方向依旧，所下降高度与水平方向距离的关系如式（8）。

本文采用SBS改性沥青，沥青各项指标均满足规范要求。本文以五种力学性质差别较大的集料为研究对象。五种集料分别为酸性的闪长岩[3]、碱性的石灰岩和中性的玄武岩[4]，测试了集料的轮廓偏斜度[5]，如表1所示。

式中 h为此时的高度；0R为该段水平方向上盘旋圆的半径，代入求解出该阶段所对应的 lΔ； hΔ 为该阶段的降落高度。

2.4 着舰段

在盘旋调整段，当翼伞再次到达P3点时，则进入最后的着舰段，该阶段翼伞沿P3点切向飞出，最终将着陆至目标点O处，此时采取式（1）的径向归航方式，由翼伞系统根据目标点的微小偏差来控制。

由于在舰船上着陆，对翼伞在最终时刻的速度方向有严格要求，相比于传统的翼伞分段归航方案，该方案是一个全过程的控制方案，过程中不会失去目标点，能够达到末段速度方向的要求。

3 动目标归航方案

由于实际舰船为动目标，可将原始落点O(0,0,0)参数化为最终落点O'(0 +Δ x,0 +Δ y, 0 +Δ z)，Δ x, Δ y, Δz分别为水平方向和高度方向上的位置变化。

以渤海为例，其他参数估计为，在海洋中，舰船在非机动状态下，随洋流作牵连运动，洋流流速为vs=0.5～1m/s，假设洋流流速在该范围内，同时舰船还受海面风影响，风力级别与风速以及对海浪高度的影响对应关系见表2。

表2 风力风速浪高对应关系Tab.2 The relationship among wind power′ speed and wave height

综合考虑风速和海况的影响，要求着陆风力在4级及以下较为合理，即风速范围为6m/s以内，浪高范围在±1m以内。舰船在水平方向上的运动主要由洋流流速影响，在高度方向上的变化受浪高影响。

考虑到舰船会沿着洋流的方向做牵连运动，针对着陆末段的舰速、伞速、风速和水速进行估计与分析，得出结论，逆风着陆对舰船航速的要求较低，所以应选择逆风着陆。

依据静目标归航的方案进行改进，运动过程中翼伞系统的坐标为 A(x, y, z)，目标点坐标为O'(0 +Δ x,0 +Δy , 0 +Δz )，做差得到相对坐标A'(x -Δ x, y -Δy , z -Δ z)。同理，套入上一章所提出的静目标归航的方法。航迹俯视图如图6所示。

这个过程中需要实时采集无人机和舰船的位置坐标，求出相对坐标，代入第2章中的各步骤，以及通过无人机采集空中的风速风向等数据以便更精准地计算，根据当前高度和实时的落点预估最终落点。

式中 vz为翼伞稳定下降时的竖直方向速度； vb为舰船随着海风和洋流运动的对地速度；s为舰船最终会行驶的位移；t为预估剩余降落时间。

修正该点坐标，舰船坐标叠加s即为最终舰船目标点坐标，通过实时计算来修正该点。

在着陆末段，舰船与翼伞系统同方向运动，可以使舰船加速运动，并操纵翼伞做减速运动，使无人机与舰船的相对速度最小，确保安全着舰。

4 仿真分析

4.1 模型参数的选定

根据所提出的方法利用 MATLAB/Simulink软件模块搭建仿真模型，采用六自由度模块进行动力学计算。依据方案将整个归航控制模块分为阶段判断模块、攻角侧滑角计算模块、控制量计算模块、力和力矩计算模块等。

根据国内某型号的实验数据，仿真参数的选取如表3所示。

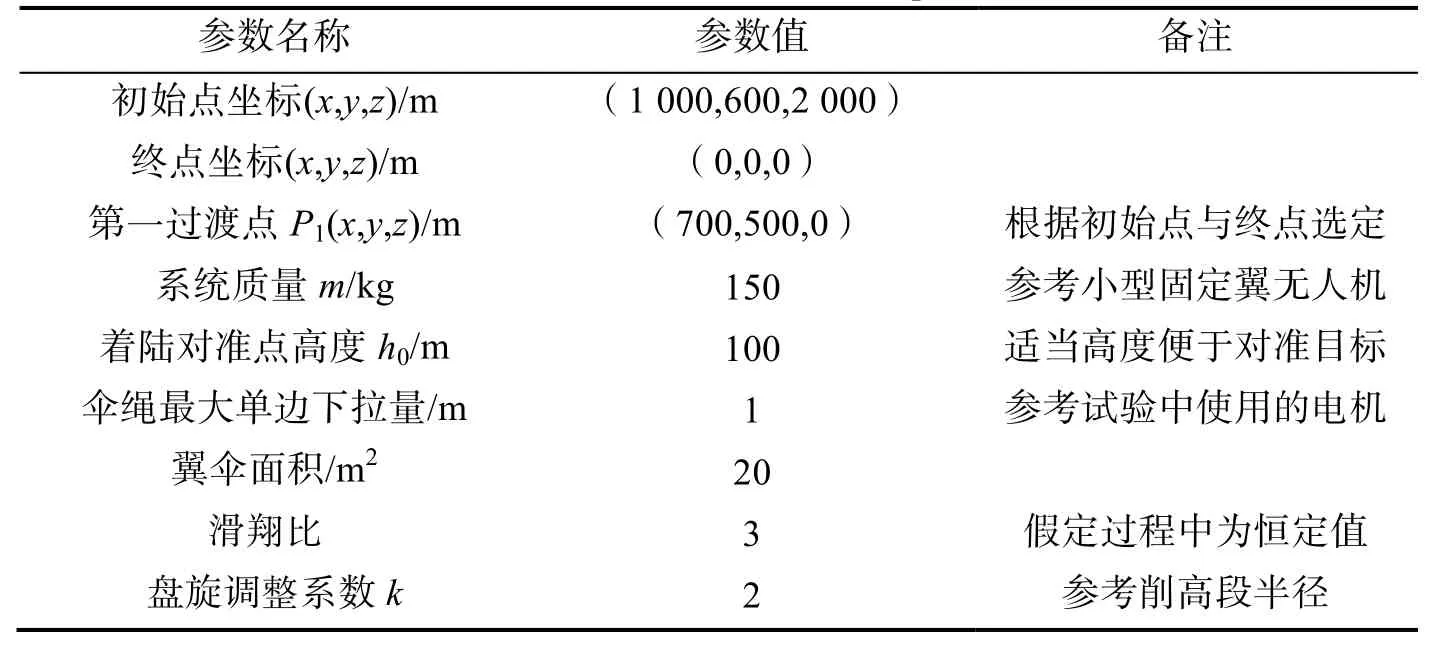
表3 仿真参数的选取Tab.3 The selection of simulation parameters

对无风、静目标的情况进行了仿真计算，同时假定伞绳下拉的响应足够迅速，可以忽略不计，仿真结果如下。

4.2 静目标仿真结果及分析

为了比较静目标归航控制方案与传统分段归航控制方案在落点精度上的差距，针对上述仿真模型，分别采用两种控制方案进行仿真。首先采用传统的分段归航控制方案，仿真得到的出整体航迹和俯视图如图7所示。

最终落点坐标为（- 1 66,- 171,0），距落点的直线距离为 238m，若采用本文所提出的静目标归航控制方案，仿真得到整体航迹和俯视图如图8所示。

根据该仿真结果可以看出，落点坐标为(- 64,55,0)，与预期目标点(0,0,0)距离为 84m，仍有一定误差，于是考虑在盘旋调整段对下拉量进行自主修正，得到修正后的仿真图如图9所示。

在对盘旋调整段进行矫正后，最终落点坐标为(-3 9,8,0)，距目标点直线距离为40m。

4.3 动目标仿真结果及分析

考虑到舰船为可控的动目标，在最后的着舰段，协同机动可以有效消除沿舰船方向上的误差，可以实现精确着舰。同样采用表4中的仿真参数，并在翼伞进入着舰段时，令舰船开始沿x轴负方向（即翼伞运动同向）以一固定速度开始运行。仿真得到的出整体航迹和俯视图如图10所示，着舰区域如图11所示。

根据该仿真结果显示，在着舰段对舰船协同机动，最终落点坐标为(-7 7,-2 ,0)，此时舰船所到达的目标点为(- 78,0,0)，两点直线距离为2.3m。

对于上述传统归航控制方案、静目标归航控制方案、校正后的静目标归航控制方案以及动目标归航控制方案的四个算例中，伞绳下拉量随时间变化的示意图如图12所示。

从图12可以看出，对于的传统归航方案，在盘旋削高阶段伞绳下拉量基本恒定，而本文所提出的归航方案在盘旋削高阶段可以根据当时的飞行轨迹调整下拉量，进而改变转弯半径为最终精确着舰做好准备。对于图12（b）和图12（c）可以看出，主要区别在于盘旋调整段的下拉量及时长，修正后，该阶段的转弯半径变大，以提高着舰精度。对于图 12（d）最终着舰段的下拉量更趋于零，说明末端不需较大的转弯，即更稳定。

不同归航方法落点偏差对比见表4。

表4 不同方案的落点坐标Tab.4 Falling point coordinates of different methods

对上述仿真结果进行对比分析，可以得出：

1）静目标归航控制方案能够将落点精度从238m提高到100m以内，但仍和预期目标有一定差距，于是考虑在盘旋调整段对下拉量进行修正，矫正方法为在翼伞运动过程中时刻检验当前的转弯半径与预期转弯半径的差值，并对当前半径进行修正以达到预期转弯半径。

2）矫正后的归航控制方案可将落点精度提高到 50m范围内。若在着陆末段结合传统归航方案的雀降方法，可达到最小误差。

3）将舰船作为可控的动目标，在翼伞的着陆末段协同控制，可以有效地将落点误差控制到5m以内，实现精确着舰。

5 结束语

本文以无人机—翼伞系统着舰为背景，通过分析着舰时的精度需求，对传统的分段归航控制方案进行分析，提出了一种改进的静目标归航控制方案，对方案中各阶段进行了阐述和目的介绍，对不同的方案分别进行了仿真计算，并根据仿真结果对方案进行修正。仿真结果表明：本文所提出的静目标归航控制方案，能够控制着陆末段的速度方向，以达到着舰要求，同时可以有效地提高着陆精度，从而实现无人机精确着舰。

References)

[1]Office of the Secretary of Defense. Unmanned Aircraft Systems Roadmap 2005-2030[R]. Washington DC： Office of the Secretary of Defense, 2005： 37-40.

[2]刘强. 无人机自动着舰撞网回收技术研究[D]. 南京： 南京航空航天大学, 2010： 1-9. LIU Qiang. Research on UAV Ship Landing System Based on Net Recovery[D]. Nanjing： Nanjing University of Aeronautics and Astronautics, 2010： 1-9. (in Chinese)

[3]裴锦华. 无人机撞网回收的技术发展[J]. 南京航空航天大学学报, 2009, 41(增刊2)： 6-11. PEI Jinhua. Technology Development of UAV Net Recovery System[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(sup2)： 6-11. (in Chinese)

[4]熊菁, 程文科, 秦子增. 基于Serrt-Frenet坐标系的翼伞系统轨迹跟踪控制[J]. 动力学与控制学报, 2005, 3(2)： 87-91. XIONG Jing, CHENG Wenke, QIN Zizeng. Path-following of Parafoil System Based on Serret-frenet[J]. Journal of Dynamics and Control, 2005, 3(2)： 87-91. (in Chinese)

[5]HEWGLEY C, YAKIMENKO O. Precision Guided Airdrop for Vertical Replenishment of Naval Vessels[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Seattle, Washington. AIAA 2009-2995, 2009.

[6]HEWGLEY C, YAKIMENKO O. Shipboard Landing Challenges for Autonomous Parafoils[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland. AIAA-2011-2573, 2011： 2-21.

[7]唐大全, 杨迎化, 杜鑫. 无人机自动着舰末段机器视觉导引方法研究[J]. 航空计测技术, 2004, 24(2)： 4-9. TANG Daquan, YANG Yinghua, DU Xin. Study of the Guidance Methods of Machine Vision During the Last Phase of Auto-landing of UAV on Deck[J]. Metrology & Measurement Technology, 2004, 24(2)： 4-9. (in Chinese)

[8]陈瑞明. 翼伞精确定点着陆归航方法研究[J]. 航天返回与遥感, 2005, 26(1)： 18-23. CHEN Ruiming. Homing Method Research of Precision Landing of Pafafoil-system[J]. Spacecraft Recovery & Remote Sensing, 2005, 26(1)： 18-23. (in Chinese)

[9]李春, 吕智慧, 黄伟, 等. 精确定点归航翼伞控制系统的研究[J]. 中南大学学报, 2012, 43(4)： 1331-1335. LI Chun, LYU Zhihui, HUANG Wei, et al. Guidance Navigation & Control System Forprecision Fix-point Homing Parafoil[J]. Journal of Central South University, 2012, 43(4)： 1331-1335. (in Chinese)

[10]李德荣, 陈楸, 吴泽锐, 等. 翼伞转弯机理及其影响因素仿真分析[J]. 电子设计工程, 2014(19)： 57-60. LI Derong, CHEN Qiu, WU Zerui, et al. Simulation Analysis of Parafoil Turn Mechanism and Its Influence Factors[J]. Electronic Design Engineering, 2014(19)： 57-60. (in Chinese)

[11]王利荣. 降落伞理论与应用[M]. 北京： 宇航出版社, 1997： 494-498. WANG Lirong. Parachute Theory and Application[M]. Beijing： Aerospace Press, 1997： 494-498. (in Chinese)

[12]史献林, 余莉. 翼伞空中回收系统的研究及其进展[J]. 航天返回与遥感, 2008, 29(1)： 1-10. SHI Xianlin, YU Li. The Study and Development of the Parafoil Mid-air Retrieval System[J]. Spacecraft Recovery & Remote Sensing, 2008, 29(1)： 1-10. (in Chinese)

[13]CARTER D, GEORGE S, HATTIS P, et al. Autonomous Large Parafoil Guidance, Navigation, and Control System Design Status[C]//19th AIAA Aerodynamic Decelerator System Technology Conference and Seminar. Williamsburg, VA, 2007： 1-15.

[14]PATEL S, HACKETT N R, JORGENSEN D S. Qualification of the Guided Parafoil Air Delivery System-light (GPADS-light)[C]//14th AIAA Aerodynamic Decelerator Systems Technology Conference, San Francisco, CA, 1997： 234-243.

[15]STEIN J M, MADSEN C M, STRAHAN A L. An Overview of the Guided Parafoil System Derived from X-38 Experience[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Arlington, Virginia, 2005： 1652-1665.

Homing Method of Controllable Parafoil for Landing of UAV on Deck

WANG Di TENG Haishan WU Shitong
（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Carrier unmanned aerial vehicle (UAV) is a development trend in the future. Now how the UAV accurately and safely landing on a small ship is a key technology needed to be solved. This paper introduces a kind of method which UAV can accurately land on a small ship with a controllable parafoil. Based on the traditional multiphase homingmethod, it designs an improved control method with independent correction during the last phase, improving the accuracy effectively. Cooperated with the controllable moving target, parafoil with UAV can land on deck accurately. The paper builds a homing control pathplanning model, it carries out the simulation and analysis with MATLAB, and verifies the feasibility of this method. Comparing with the traditional homing method, this method can significantly improve the landing accuracy.

parafoil; unmanned aerial vehicle (UAV); multiphase homing; moving target; path planning; landing on deck

V445

A

1009-8518(2017)03-0043-10

10.3969/j.issn.1009-8518.2017.03.005

王帝，男，1991年生，2014年获天津大学自动化专业学士学位，现在中国空间技术研究院攻读硕士学位。研究方向为航天器返回与着陆。E-mail： wangdi9112@163.com。

（编辑：陈艳霞）

2017-03-29