WSNS中基于箱线图的误差自校正定位算法*
金仁成,李应琛,马远,赵继鹏
(大连理工大学 辽宁省微纳米技术及系统工程重点实验室,大连 116024)
WSNS中基于箱线图的误差自校正定位算法*
金仁成,李应琛,马远,赵继鹏
(大连理工大学 辽宁省微纳米技术及系统工程重点实验室,大连 116024)
针对基于接收信号强度指示(RSSI)的无线传感器网络(WSNs)节点定位技术易受环境影响、算法运算量大等问题,提出一种基于箱线图的误差自校正定位算法。该算法采用箱线图法处理测距过程中的异常RSSI值,利用自校正最小二乘法消除测距误差进而实现节点定位。仿真和实验结果表明,该算法可以有效抑制异常RSSI值,显著提高节点定位的准确性和稳定性,而且无需建立复杂的数据传播模型或构造RSSI位置指纹分布图。
无线传感器网络;箱线图;误差自校正;定位算法
引 言
现有无线传感器网路定位算法主要分为两大类[4]:基于测距的定位算法和无需测距的定位算法。无需测距的定位算法依靠网络的连通度、路由表及通信半径等信息实现未知节点的定位,具有节点硬件要求低、网络能耗开销小的优势,但定位误差高于基于测距的定位算法。基于测距的定位算法主要包括两个阶段:测距阶段和定位阶段。测距阶段通常采用的测距技术包括:到达时间(TOA)、到达时间差(TDOA)、接收信号强度指示(RSSI)、到达角度(AOA)。
国内外研究者做了大量的研究工作。在测距阶段,参考文献[7]将测距误差进行了详细分类,并用狄克逊检验法去除异常RSSI值。参考文献[8]将Hampel 滤波器与核密度(HF&KDE)估计相结合,利用置信指数来检测测距误差,但是该方法计算复杂,不适用于能耗受限的无线传感器网络。参考文献[9]利用高斯双峰的空间关联度,有效地降低了障碍物对信号强度的影响,实现了复杂非视距环境下RSS定位。但在实际环境中,信号传播模型实时变化,难以准确评估。在定位阶段,参考文献[10]提出一种加权最小二乘估计算法(WLSE),利用距离信息作为权重参考,但该算法没有考虑测距误差对定位阶段的影响。参考文献[11]也提出一种加权最小二乘定位算法,结合测距误差和定位误差作为加权权重,但该算法计算复杂度较大,环境适应能力较差,不利于应用于处理能力受限的无线传感器网络。
针对现有定位算法中计算复杂、能量损耗大、定位精度低等问题,本文提出一种基于箱线图的误差自校正定位算法,有效地降低了外界环境对测距精度的影响,提高了定位的精度且无需额外的通信开销。
1 基于RSSI的测距阶段
1.1 基于RSSI的测距模型
基于RSSI的测距方法是无线接收机通过测量接收的信号功率来确定与无线发射机之间的距离。其中无线信号的传播模型通常可以分为理论分析模型、经验模型和混合模型[13]。理想传播环境下的自由空间模型(Friis)可以作为一种理论分析模型,如式(1)所示:
(1)
其中:PT为发射功率,PR(d)为接收功率,单位通常为W或者mW;GT为发射机的天线增益;GR为接收机天线增益;λ为发射信号的波长,单位为m;d为发射端与接收端之间的距离,单位为m;L为系统损耗因子。Friis模型主要用于估算接收端与发射端在无阻挡环境下视距路径所接收的功率。在实际的环境中,传播模型可能受到多径反射、衍射、障碍物等因素的影响,导致测量精度发生很大变化。无论室内还是室外信道,基于理论和测试的传播模型平均接收信号功率随距离变化而呈对数衰减。因此,本文采用对数路径损耗模型,如式(2)所示:
(2)
其中:PR(d)为距离发射机d时接收的信号强度,P0(d0)为距离发射机d0(通常为1m)时接收的信号强度,n为路径损耗指数,Xσ为均值为零、标准偏差为σ的高斯分布随机变量,单位为dB。根据经验,不同环境下的路径损耗指数和标准偏差如表1所列。
1.2 基于箱线图的异常RSSI检测
在实际的测距场景中,接收信号强度指示(RSSI)不可避免会出现异常变化,导致测距出现较大偏差,为此提出了许多检测方法滤除异常RSSI值,例如均值滤波法、3σ检测法、狄克逊(Dixon)检验法等。其中3σ异常值检测[14]已经被广泛运用到无线传感器网络中,但3σ检测法需要假设RSSI值服从标准正态分布,但真实测量的RSSI值并不总是服从标准正态分布,且判断异常值需要计算一包数据的均值和标准差,异常RSSI对均值和标准差会产生很大影响,因此利用3σ检测法判断异常RSSI值具有一定的适用范围。
针对上述问题,本文提出一种基于箱线图的异常RSSI检测方法,该方法利用测量的数据中的5个统计量:最小值、第一四分位数(所有数据中由小到大排列后第25%的数字)、第二四分位数(所有数据中由小到大排列后第50%的数字)、第三四分位数(所有数据中由小到大排列后第75%的数字)和最大值剔除数据中的异常RSSI值,方法如下:
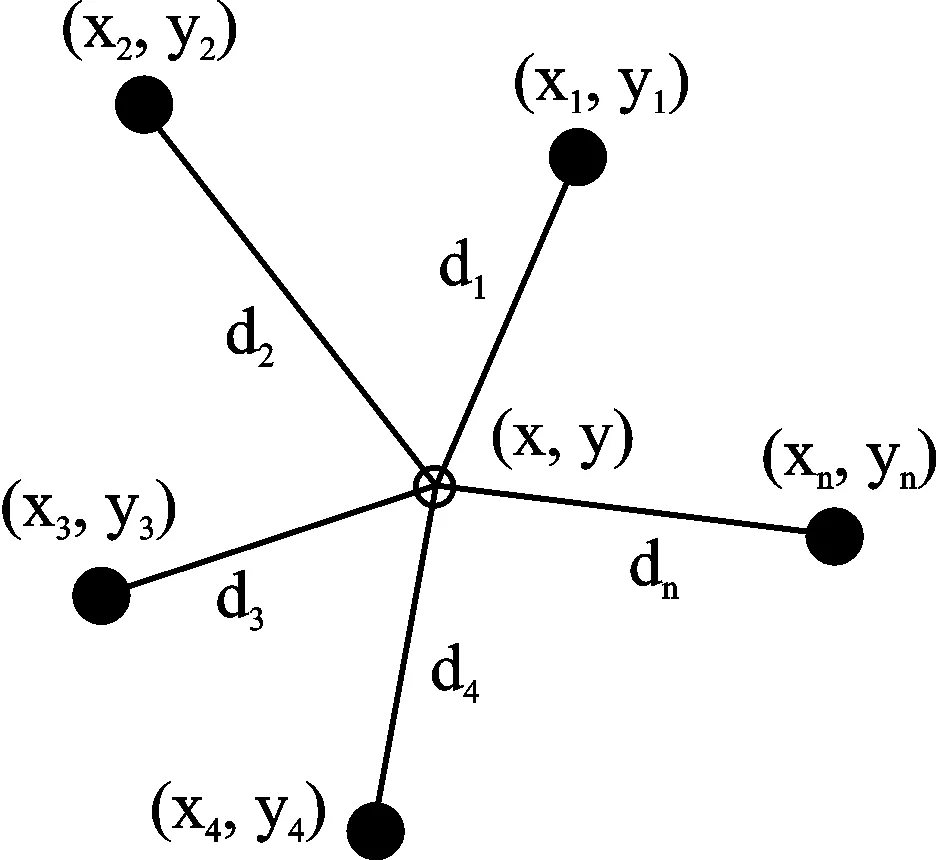
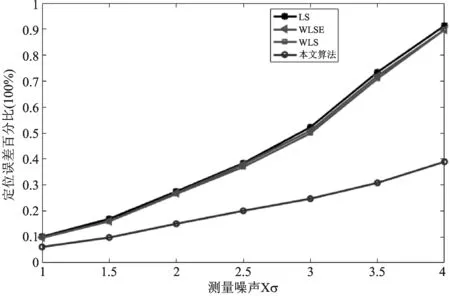
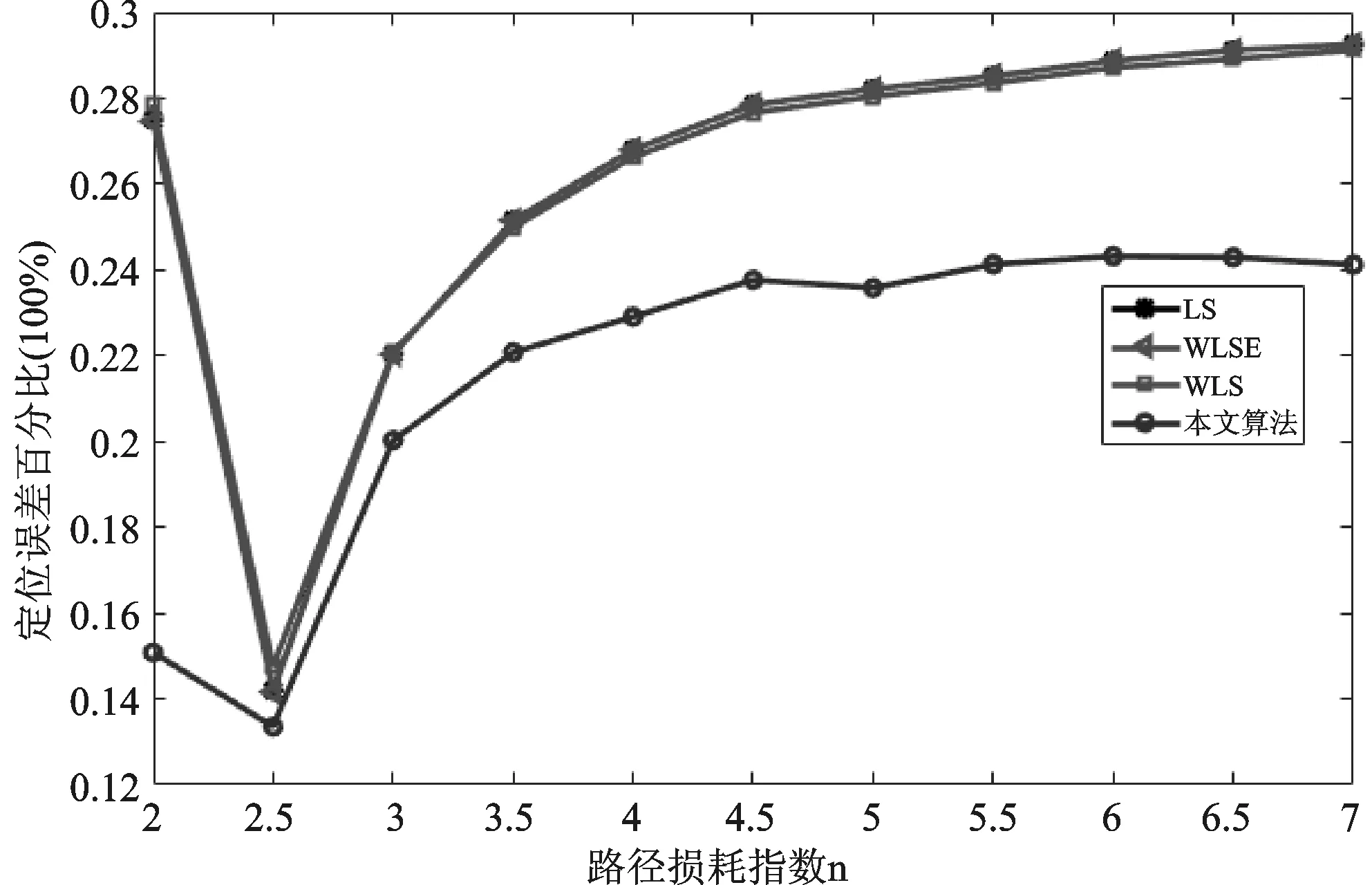
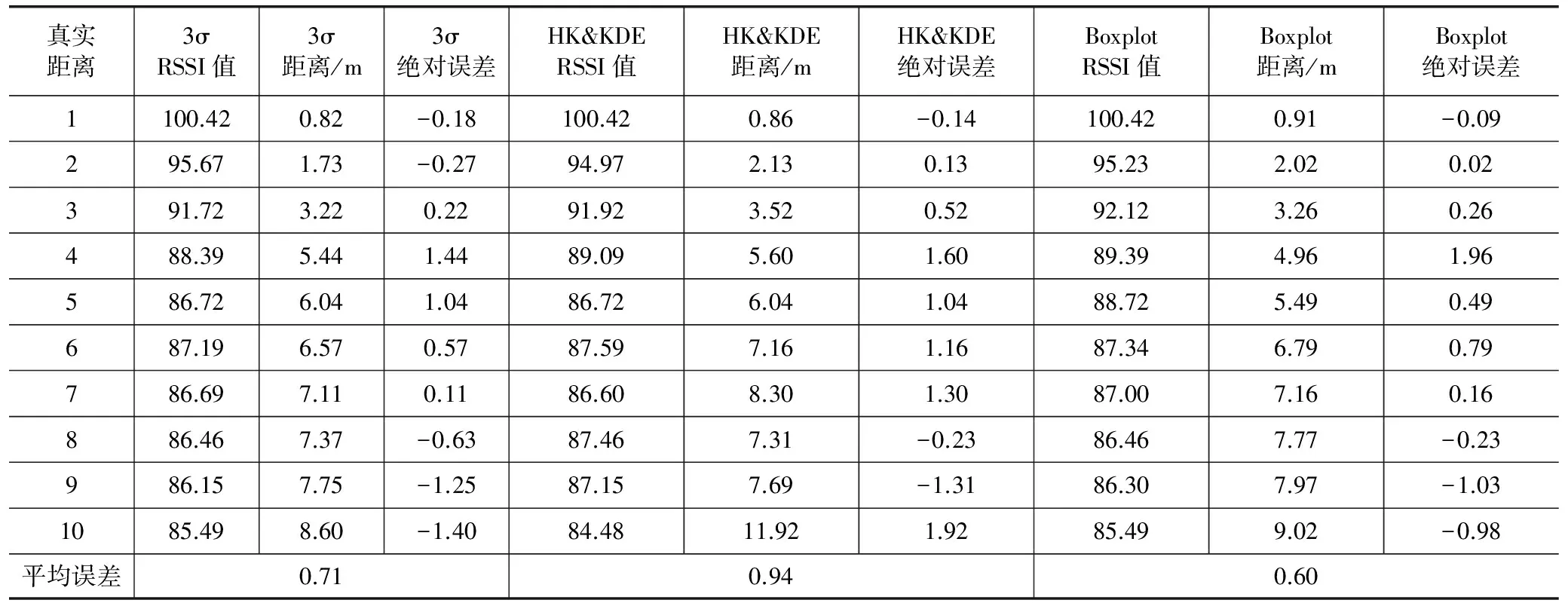
① 采集RSSI信号强度,如果lowerbounds ② 将测得的RSSI值序列RSSI∈Rn进行从小到大排序:RSSI1 ③ 计算出各分位数的位置,第一四分位数Q1=(n+1)/4,第二四分位数(中位数)Q2=(n+1)/2,第三四分位数Q3=3(n+1)/4,通过3个四分位数将数据集合分成四组,每组数据占25%;计算四分位距(Interquartile Range, IQR),IQR=Q3-Q1。 ④ 计算出异常值截断点(Outliers Cut-off Point),OCP1=Q1-1.5IQR,OCP2=Q3+1.5IQR,异常值范围为{RSSIol|RSSI ⑥ 重复上面步骤直至所有未知节点完成异常RSSI滤除。 图1 箱线图法处理流程图 实验箱线图处理异常RSSI值的流程如图1所示。箱线图法根据实际测量数据进行异常值分析处理,既不需要数据服从某种特定的概率分布,也不需要对数据做任何限制性要求,可以真实直观地反映出数据本身价值。此外,箱线图判断异常值的标准以四分位数和四分位距为基础,其中四分位数具有较好的耐抗性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以利用箱线图处理异常RSSI值计算过程简单,且具有较强的鲁棒性,更适合应用于能耗要求严格的无线传感器网络。 2.1 经典最小二乘法定位 图2 最小二乘法定位原理图 最小二乘法定位基本原理如图2所示。已知随机散布n个锚节点,其坐标为(x1,y1),(x2,y2),…,(xn,yn),未知节点坐标为(x,y)。锚节点到未知节点间的距离为:d1,d2,…,dn。 可得定位方程组: (3) 分别用方程组(3)中的前(n-1)个方程减去第n个方程,通过适当简化得到线性化方程: (4) 其中: 由于受多种因素的影响,存在一定的测距误差e,则实际线性方程为: (5) 假设 (6) 利用最小二乘法原理保证Q(x)取得最小值,对上式求导数得 (7) 如果AAT是非奇异矩阵,则解X得 (8) 然而,可以看到定位方程组解的精度取决于最后一个方程所存在的误差,即第n项的测量距离dn。如果dn的测距误差较大,即使前(n-1)项方程的测距信息十分准确,未知节点求解的位置估计值也会产生较大定位误差。为了更好解释这一问题,将方程(4)展开带有误差项,并用方程组的前(n-1)个方程减去第n个方程,可以得到方程组: (9) 2.2 误差自校正最小二乘定位算法 正如前面所述,信号衰减在无线信道内传播不可避免地会受到外界因素影响,实际RSSI值会出现一定的波动。但是如果节点间距离越近,外界因素对节点影响越小,进而测距产生的误差越低;反之,测距可能会产生较大的偏差。为了定量解释这个现象,利用式(2)的对数路径损耗模型对距离d求偏导数,得到式(10): (10) (11) 其中: (12) 根据上式近似有: (13) 以此为前提,首先将测得的未知节点到n个锚节点之间的距离d1,d2,…,dn按大小进行排序,得到式(3)所示的定位方程组,然后用相邻的两个方程进行相减,简化后得到线性方程: (14) 其中: 2.3 基于箱线图误差自校正定位算法 通过上述对测距阶段和定位阶段分析改进,提出一种基于箱线图的误差自校正定位算法,具体定位步骤如下: ① 锚节点以固定的发射功率周期性发送带有节点ID和自身位置信息的数据包。 ② 未知节点收到锚节点的位置信息后,用箱线图法剔除异常RSSI值,求取平均值RSSIavg。 ③ 在处理n个锚节点RSSI值后,将所有锚节点的RSSIavg值从大到小排序,构建RSSIavg值与距离d的映射,建立3个集合:锚节点集合Anchor={A1,A2…,An};距离集合Distance={d1,d2…,dn},其中d1 ④ 采用误差自校正最小二乘定位算法获取未知节点的位置坐标。 为了验证基于箱线图的误差自校正定位算法的可行性,与传统的LS定位算法、加权最小二乘估计算法(WLSE)、加权最小二乘定位算法(WLS)进行了比较。仿真软件采用Matlab2016a进行分析和评估,仿真环境如下:假设有6个锚节点和8未知节点随机散布在12m×12m的范围内,节点间的通信半径为12m。仿真使用对数路径损耗模型,衰减因子n设为2,测量噪声Xσ是均值为0、标准偏差为2的高斯随机变量。根据传感器实际性能设定距离为1m时,接收信号强度P0为40dB。作为衡量定位精度标准,定位误差定义为: (15) 仿真结果表明,基于箱线图的误差自校正定位算法具有很好的定位性能。为了降低节点分布对定位结果的影响,更好地验证算法的有效性,在不同的网络拓扑结构下进行了50次仿真实验,仿真结果如图3所示。可以清晰地看到本文算法平均定位误差大约为15.03%,而LS、WLSE和WLS的平均定位误差分别大约为27.49%、26.87%、26.52%。通过比较分析,基于箱线图的误差自校正定位算法定位误差明显低于其他算法。 图3 平均定位误差对比图 在实际环境中,传播模型实时变化、不同的仿真参数可能会导致不同定位误差。为了更加贴合实际场景,分别对衰减因子n和测量噪声Xσ进行分析,对每个参数依次仿真50次,然后计算定位误差均值。 图4和图5描述了对数路径损耗模型中不同的测量噪声和路径损耗指数对定位误差的影响。可以清晰地看到:本文算法定位误差明显低于其他三种定位算法定位误差,即使在复杂多变环境下,基于箱线图的误差自校正定位算法仍能提供较好的定位信息服务,具有较高的稳定性和耐抗性。 图4 测量噪声对定位误差影响对比图 图5 路径损耗指数对定位误差影响对比图 4.1 实验平台 实验中使用的无线传感器节点为JN5148节点,是英国Jennic公司推出的高性能、低功耗的无线SoC模块,集成了所有的射频组件和无线微控制器。JN-5148有5种不同程度的功率消耗模式,考虑到能量功耗和通信性能,选择标准模块JN5148-001-M03,其分辨率为1 dB,获得RSSI值的范围是[20,108]。 4.2 测距实验分析 为了更好地理解RSSI的特性,利用两个传感器节点在学校体育场草地上进行测距实验,地面22.7°,芯片20.6°,大气湿度30%。传感器节点一个作为发射端,一个作为接收端,测量沿直线从1 m到10 m,间隔1 m测量一次RSSI值,每个位置处测量100次。 由于多径、遮蔽效应的影响,RSSI值不可避免地出现 一些剧烈波动,如果不及时剔除异常RSSI值,可能会引起较大的测距误差。为了进一步分析RSSI分布,将10个位置采集的RSS正则化,利用概率密度函数描述每个位置处的RSS。如图6所示,可以直观地看到并不是所有的RSSI分布都服从标准正态分布,有时RSSI分布会出现左偏峰或者是双峰的现象。 从表2中可以看到在某些位置处3σ检测和HF&KDE检测可能优于箱线图方法,但基于箱线图法的平均距离误差为0.60m,低于3σ检测的0.71m以及HF&KDE检测的0.94m。测距精度得到明显改善,此外该方法计算简单且行之有效,能较好地满足无线传感器网络低功耗的需求。 图6 正则化RSS概率密度函数 真实距离3σRSSI值3σ距离/m3σ绝对误差HK&KDERSSI值HK&KDE距离/mHK&KDE绝对误差BoxplotRSSI值Boxplot距离/mBoxplot绝对误差1100.420.82-0.18100.420.86-0.14100.420.91-0.09295.671.73-0.2794.972.130.1395.232.020.02391.723.220.2291.923.520.5292.123.260.26488.395.441.4489.095.601.6089.394.961.96586.726.041.0486.726.041.0488.725.490.49687.196.570.5787.597.161.1687.346.790.79786.697.110.1186.608.301.3087.007.160.16886.467.37-0.6387.467.31-0.2386.467.77-0.23986.157.75-1.2587.157.69-1.3186.307.97-1.031085.498.60-1.4084.4811.921.9285.499.02-0.98平均误差0.710.940.60 4.3 定位实验分析 图7 定位实验节点分布示意图 定位实验同样在体育场草地上进行。选用10个JN5148标准功率模块节点,其中有6个锚节点和4个未知节点,随机散布在12 m×12 m的区域内,JN5148传感器节点分布如图7所示。 在定位过程中,未知节点UN1、UN2、UN3 和UN4分别接收来自6个锚节点的RSSI值,采用基于箱线图的误差自校正定位算法实现未知节点定位,分别与传统的LS定位算法、加权最小二乘估计算法(WLSE)、加权最小二乘定位算法(WLS)进行比较,定位误差如表3所列。 表3 四种算法定位结果比较 参考文献 [1] Yang K.Wireless sensor networks[J].Principles,Design and Applications,2014. [2] Campos A N,Souza E L,Nakamura F G,et al.On the impact of localization and density control algorithms in target tracking applications for wireless sensor networks[J].Sensors,2012,12(6):6930-6952. [3] Sacks L,Britton M,Wokoma I,et al.The development of a robust,autonomous sensor network platform for environmental monitoring[J].IOP Sensors and their applications XII,2003. [4] Suo H,Wan J,Huang L,et al.Issues and challenges of wireless sensor networks localization in emerging applications[C]//Computer Science and Electronics Engineering (ICCSEE),2012 International Conference on IEEE,2012. [5] Whitehouse K,Karlof C,Culler D.A practical evaluation of radio signal strength for ranging-based localization[J].ACM SIGMOBILE Mobile Computing and Communications Review,2007,11(1):41-52. [6] Wu K,Xiao J,Yi Y,et al.CSI-based indoor localization[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(7):1300-1309. [7] Zhang C,Zhou X,Gao C,et al.On improving the precision of localization with gross error removal[C]//Distributed Computing Systems Workshops,28th International Conference on IEEE,2008. [8] Chen Y C,Juang J C.Outlier-detection-based indoor localization system for wireless sensor networks[J].International Journal of Navigation and Observation,2012. [9] Chuku N,Pal A,Nasipuri A.An RSSI based localization scheme for wireless sensor networks to mitigate shadowing effects[C]//Southeastcon, 2013 Proceedings of IEEE,2013:1-6. [10] 王建刚,王福豹,段渭军.加权最小二乘估计在无线传感器网络定位中的应用[J].计算机应用研究,2006(9):41-43. [11] Jun Z G,Xin L,Long X Z,et al.Weighted Least Square Localization Algorithm Based on RSSI Values[C]//Instrumentation and Measurement,Computer,Communication and Control (IMCCC),2015 Fifth International Conference on IEEE,2015:1236-1239. [12] Anderson D R,Sweeney D J,Williams T A,et al.Statistics for business & economics[M].Nelson Education,2016. [13] Goldsmith A.Wireless communications[M].Oxford city:Cambridge university press,2005. [14] Jin R,Xu H,Che Z,et al.Experimental evaluation of reducing ranging-error based on receive signal strength indication in wireless sensor networks[J].IET Wireless Sensor Systems,2015,5(5):228-234. [15] Wang L,Baker A J.Critical Power for Vanishing of Isolated Nodes in Wireless Networks with Log-Normal Shadowing[C]//Mobile Ad-Hoc and Sensor Systems (MASS),2013 IEEE 10th International Conference on IEEE,2013:46-54. [16] Jin R,Peng B,Meng L,et al.Research on localization method based on RSSI ranging-error compensation[C]//Wireless Communications,Networking and Mobile Computing,WiCom'09. 5th International Conference on IEEE,2009:1-3. 金仁成(副教授),研究方向为无线传感器网络、物联网;李应琛(研究生),研究方向为无线传感器网络定位技术、室内定位技术;马远(研究生),研究方向为无线传感器网络定位技术;赵继鹏(研究生),研究方向为无线传感器网络路由技术。 Boxplot-based Error Self-calibration Localization Algorithm in WSNs Jin Rencheng,Li Yingchen,Ma Yuan,Zhao Jipeng (Key Laboratory for Micro/Nano Technology and System of Liaoning Province,Dalian University of Technology,Dalian 116024,China) In order to solve the problem of wireless sensor network (WSNs) node location technology based on signal strength indication (RSSI), which is easy to be influenced by the environment,and the algorithm has a large amount of computation and so on,a boxplot-based error self-calibration localization algorithm is proposed.The algorithm selects an adaptive distance estimation method based on boxplot to deal with outlier RSSI value,and uses a self-calibration least square algorithm to achieve localization by using ranging error self-elimination.The experiment results show that the proposed algorithm can effectively suppress outliers RSSI value and output a high and stable processing result while satisfying the high positioning accuracy requirement.For the above achievement,no hardware modification as well as time consuming RSSI-maps or complex signal propagation models are required. wireless sensor networks;boxplot;error self-calibration;localization algorithm 国家重点基础研究发展计划(973计划)资助项目(2009CB320300);国家“十二五”科技支撑计划资助项目(2011BAG05B02);国家基金委创新群体项目(Science Fund for Creative Research Groups of NSFC)( 51621064)。 TP393.1 A �士然 2017-02-20)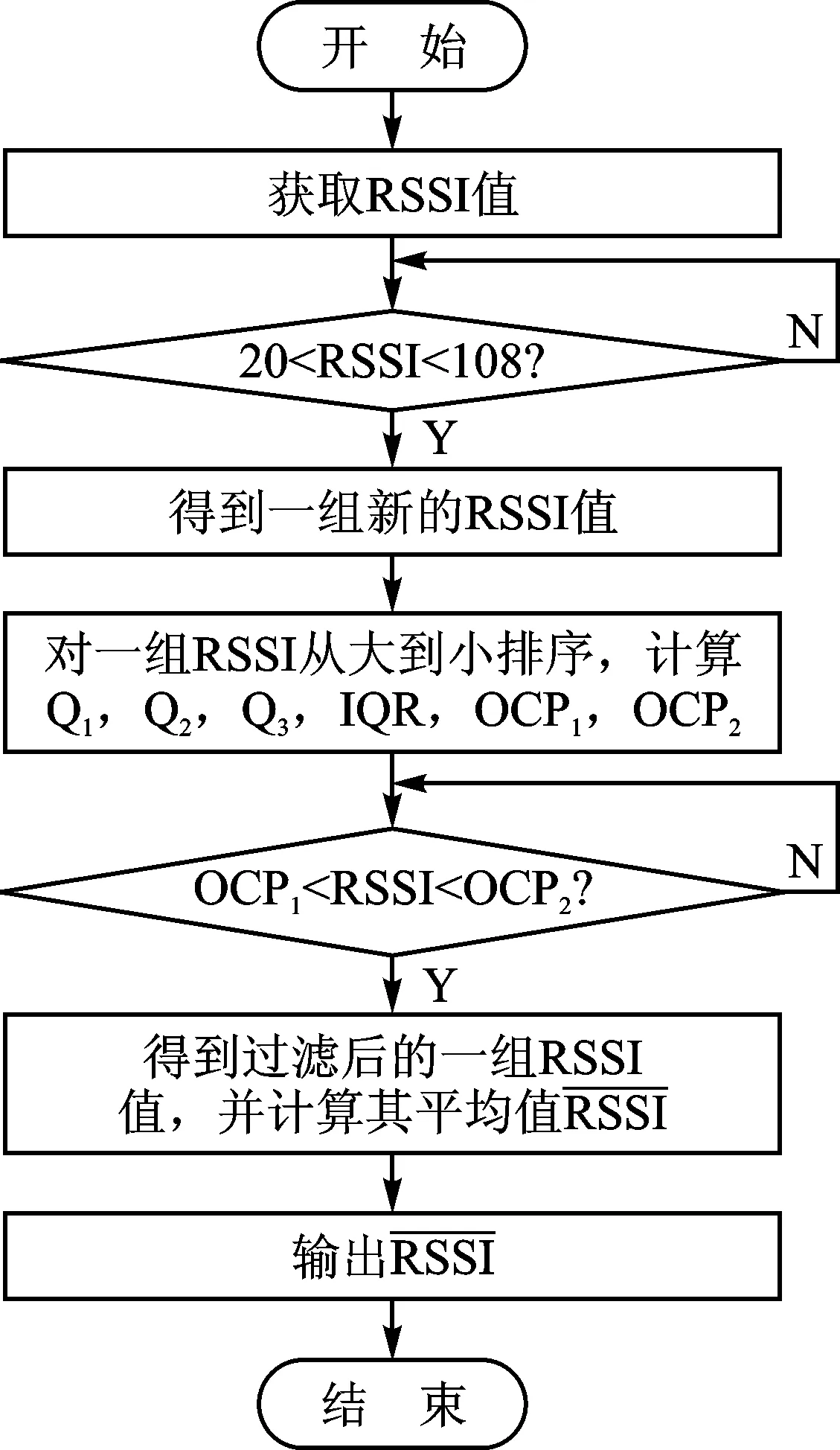
2 基于RSSI定位阶段
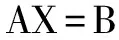
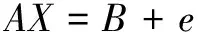
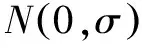
3 算法仿真及结果

4 实验仿真及结果
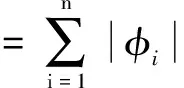



结 语


