电力负荷数据预处理研究及应用

苏舟，李灿，姚李孝，崔寒珺

（西安理工大学水利水电学院，陕西西安 710048）

电力负荷数据预处理研究及应用

苏舟，李灿，姚李孝，崔寒珺

（西安理工大学水利水电学院，陕西西安 710048）

电力系统历史负荷数据的准确与否对负荷预测效果有重要影响，首先采用减法聚类算法得到历史负荷数据的聚类数目和聚类中心，并以此来作为模糊c-均值聚类的起点，然后通过负荷曲线的横向相似性找出不良数据，最后修正不良数据，得到连续准确的负荷数据。通过实例分析验证了此方法的有效性。

不良数据；减法聚类；模糊c-均值聚类

历史负荷数据一般来源于SCADA数据库。因为一些随机的小干扰或特殊事件的发生，影响了SCADA中的数据的准确性，使SCADA数据库中出现不良数据。不良负荷数据一般分为缺失值和异常值两种[1]。缺失值一般是由于切负荷、线路检修停电或SCADA系统故障产生；异常值则通常是因为一些突发性的大事件对电力负荷造成了冲击，导致负荷异于平常。负荷的异常值通常表现为出现极大极小值、负荷毛刺现象等。电力负荷资料中存在一些不良数据，由于不良数据都是不准确的，因此在负荷预测中应用将会影响其精度[2]，为了保证负荷预测的准确性，我们需要对历史的负荷数据进行预处理，使其更加准确地接近原始值。

缺失值非常容易识别和辨认，对于缺失值，传统的处理办法有人工填写法、采用缺失值两侧数据平均值填写法、插值法等。对于异常值，在异常值较多的日期可以通过曲线置换的方法将异常的负荷曲线替换下来，若是只存在个别的孤立异常点，则可以采用分时段设定阈值的方法，超出阈值的点可以看作异常点，识别出异常点后通过公式进行修正。近年来，采用智能算法进行数据预处理的趋势非常明显，文献[3]利用离散二进小波变换系数的模极大值的位置和幅度与信号的局部奇异性密切相关的特点，提出了一种基于小波去噪的数据预处理方法，取得了良好的效果。文献[4]提出一种基于层次聚类分簇搜寻的孤立点检测算法，实例验证这种方法对孤立点的检测非常灵敏。文献[5]利用神经网络的泛化能力对不良数据进行定位，效果显著。

采用聚类法识别异常数据已经被证明是一个有效的方法，模糊c-均值聚类算法（FCM）可以很好地对历史负荷数据进行检测，将类似的值聚成一类，落在聚类集合之外的值就是异常值。但FCM其本质上是一种局部搜索的爬山法，对聚类中心的初始化相当敏感。由于模糊c-均值聚类的目标函数是一个非凸函数，这个函数存在很多的局部极值点，若初始化不当，算法将很容易收敛到局部极小值，无法收敛到全局最优解。目前还没有一种通用的理论体系对在聚类初始化时所设定的聚类中心的数目做出指导。因此本文将减法聚类算法与模糊c-均值聚类相结合，减法聚类算法可以解决FCM的初始值设定难的问题。在算法开始时先采用减法聚类算法得到聚类数目的上限，然后再通过FCM进行聚类。不但可以避免事先确定聚类中心的数目从而保证算法收敛到全局最优解，还能提高计算速度。

1 FCM算法及其改进算法

1.1 模糊c-均值聚类

模糊c-均值聚类算法是一种通过隶属度矩阵表达样本属于每类的程度的一种软聚类算法。它通过最小化目标函数来寻找隶属度μij和聚类中心vj。设输入样本为xi（i=1，2，…，M），将X分为R类，则模糊c-均值聚类的目标函数为

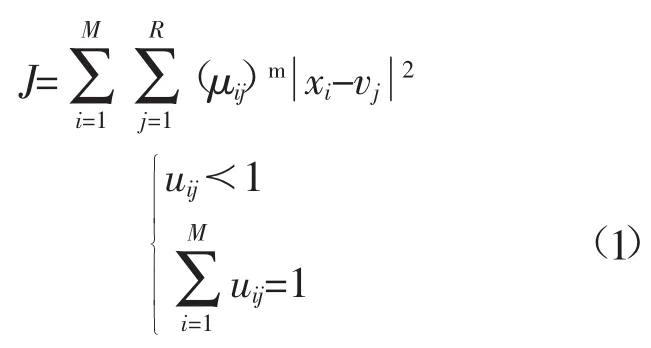
式中，m＞1为模糊因子（权重），它的大小决定了uij的模糊程度。uij（i=1，2，…，M；j=1，2，…，R）表示第i个样本属于第j类的隶属度。|xi-vj|2表示第i个样本到第j个聚类中心的距离。

每次迭结迭代计算束后通过下列公式更新迭代中心和隶属度：

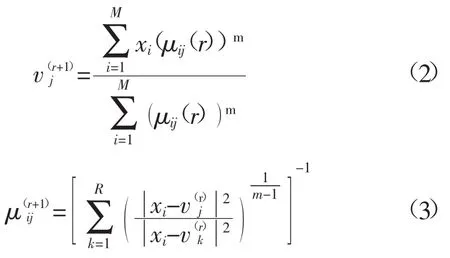
式中，r表示迭代次数。

检验|J（r+1）-J（r）|＜ε是否成立，若成立，则停止计算，输出结果；否则，返回上一步继续迭代。

1.2 减法聚类算法

令X={x1，x2，…，xn} 为p维空间Rn上的一个数据集，减法聚类算法的过程为：

1）对于样本集X中的每一个点xi（i=1，2，…，n），按照如下公式计算它们的密度指标：

选择密度指标最高的数据点xc1作为第一个聚类中心（密度指标为Dc1）。式中，表示该点的领域半径，落在半径以外的点对点xi的密度指标贡献很小。

2）对第k次选出聚类中心xck（密度指标为Dck），通过如下公式对每个点的密度指标进行修正：

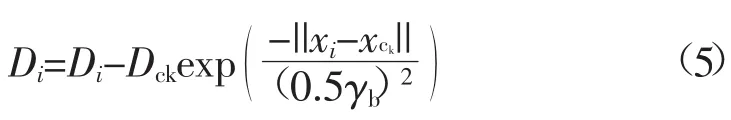
式中，γb为一个正数，一般取γb=（1.2～1.5）γa，表示一个密度指标函数明显减小的领域。γb的提出是为了避免出现相距很近的聚类中心。

在修正后的数据点中选出密度指标最高的点xck+1作为新的聚类中心。

3）判断

是否成立。若成立，则退出运行；否则，重复（2），直到满足条件为止。式中，预先给定的参数δ＜1决定了最终产生的初始化聚类中心的数量。δ越小，产生的聚类数越多。

2 改进FCM算法进行数据预处理

由以上介绍可知，减法聚类算法的聚类中心出现的顺序与其密度指标的大小有关，密度指标越大，则聚类中心越早出现。即越早出现的聚类中心越有可能是FCM初始化时的合理聚类中心。因此，在进行FCM的计算时，若希望得到i个聚类中心，则只需要选取通过减法聚类算法产生的前i个聚类中心作为FCM的初始聚类中心来进行计算，而不需要再重新进行初始化，大大提高了FCM算法的效率。其改进算法的流程如图1所示。

将这种用减法聚类算法改进的FCM算法应用与电力负荷数据的预处理上，具体操作步骤为：

1）通过改进FCM算法对负荷数据进行聚类，得到聚类数目i*和聚类中心

2）计算各时刻对应于聚类中心的均方差：

图1 改进FCM聚类Fig.1 Improved Fuzzy c-means clustering

3）通过下式判断此类数据中是否包含有不良数据：

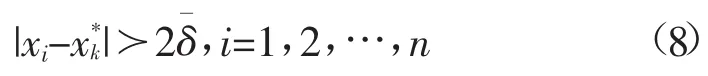
若满足（8）式，则此数据为不良数据。

4）设共生成i*条特征曲线，不良数据存在于被检曲线Xd的p点到q点，其特征曲线为Xt，修正曲线为Xr，则通过下式修正不良数据：

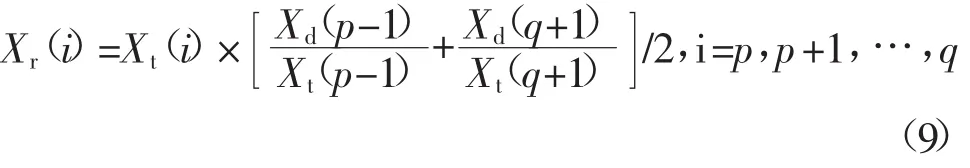
3 算例分析

以某地1998年负荷数据为例验证算法的有效性。采用日48点负荷数据，随机抽取其中一天的数据作为样本。

3.1 负荷数据预处理

数据处理前后如图2—图3所示，对比图2与图3，我们注意到，图2的负荷曲线不够连续，存在明显的突变现象，有两处不良数据需要修正，而在图3中这一现象已经被修正后的数据取而代之，保证了负荷曲线的平滑与准确。

3.2 数据处理前后负荷预测结果对比

图4和图5分别为某日的48点历史负荷数据处理前和处理后对后一天的的负荷预测结果，从图中可以清楚地看到数据处理后的负荷预测效果更好。

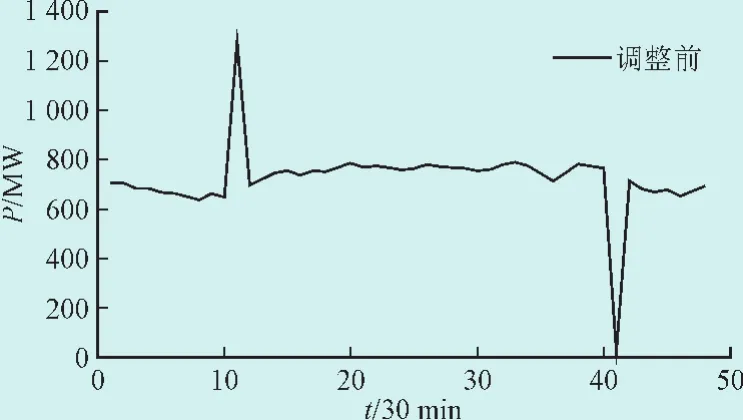
图2 数据处理前Fig.2 Unprocessed data

图3 数据处理后Fig.3 Processed data

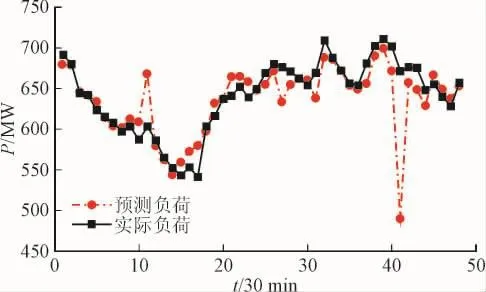
图4 含有不良数据的负荷预测结果Fig.4 Prediction result with the negative load data

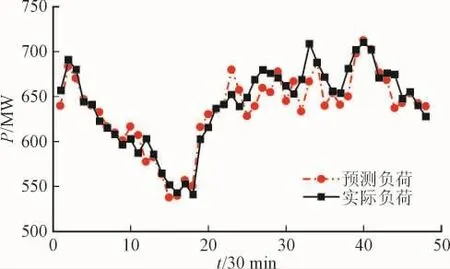
图5 数据处理后的负荷预测结果Fig.5 Prediction result with the correct load data

数据处理前后进行负荷预测的误差如图6-图7所示。

从两图的误差对比可以看到，相对于负荷预测结果而言，数据处理后误差明显减小，提高了确保了负荷预测的精度。表1给出了数据处理前后各时刻的平均误差，进一步说明了数据预处理的重要性和必要性。

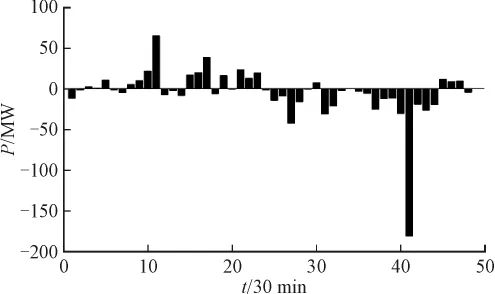
图6 含有不良数据的样本进行负荷预测的误差Fig.6 error analysis of the prediction with the negative load data

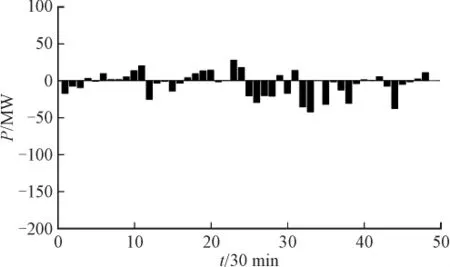
图7 处理后的样本进行负荷预测的误差Fig.7 Error analysis of the prediction with the correct load data

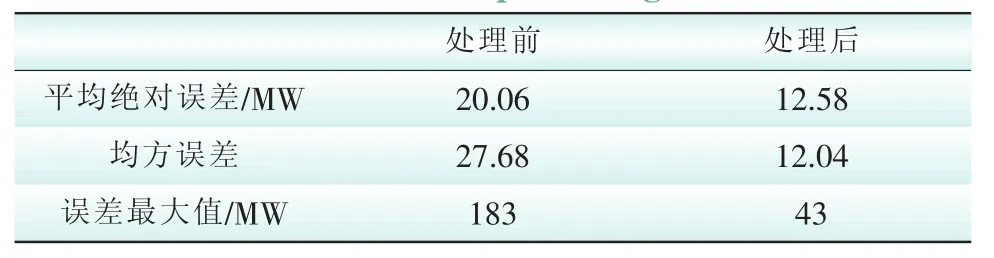
表1 数据处理前后负荷预测误差对比Tab.1 Comparison of load prediction errors before and after data processing

4 结论

1）通过减法聚类初始化FCM，取得了较快的运算速度，同时得到了合理的FCM的聚类中心，解决了FCM易于陷入局部最优和聚类中心选取过分依赖人为选择的缺点。

2）将该组合聚类算法应用到电力负荷数据的预处理问题上，能较为全面地检测出负荷冲击、负荷毛刺、极大极小值等不良数据。实现了负荷数据的优化与处理，提高了电力系统负荷预测的精度。

[1]程开明.统计数据预处理的理论与方法述评[J].统计与信息论坛，2007，22（6）：98-102.CHENG Kaiming.The theory and methods of data preparation：an overview[J].Statistics and Information Forum，2007，22（6）：98-102（in Chinese）.

[2]王成纲，郭辉，张文静.基于小波分解的电力系统短期负荷预测方法研究[J].河北电力技术，2010，29（2）：11-14.WANG Chenggang， GUO Hui， ZHANG Wenjing.Research on power system short term load forecasting method based on wavelet decomposition[J].HEBEI Electric Power，2010，29（2）：11-14（in Chinese）.

[3]李慧，杨明皓.小波分析在电力系统不良数据辨识中的应用[J].继电器，2005，33（3）：10-20.LI Hui，YANG Minghao.Application of wavelet analysis to bad data identification for power system[J].Relay，2010，29（2）：11-14（in Chinese）.

[4]许必宵，陈升波，韩重阳，等.改进的数据预处理算法及其应用[J].计算机技术与发展，2015，25（12）：143-151.XU Bixiao，CHEN Shengbo，HAN Chongyang，et al.Improved data preprocessing algorithm and its application[J].Computer Technology and Development，2015，25（12）：143-151（in Chinese）.

[5]张国江，邱家驹，李继红.基于人工神经网络的电力负荷坏数据辨识与调整[J].中国电机工程学报，2001，21（8）：104-107.ZHANG Guojiang，QIU Jiaju，LI Jihong.Outlier identification and justification based on neural network[J].Proceeding of the CSEE，2001，21（8）：104-107（in Chinese）.

[6]叶锋，何桦，顾全，等.EMS中负荷预测不良数据的辨识与修正[J].电力系统自动化，2006，30（15）：85-88.YE Feng，HE Hua，GU Quan，et al.Bad data identification and correction for load forecasting in Energy Management System[J].Automation of Electric Power System，2006，30（15）：85-88（in Chinese）.

[7]肖春景，张敏.基于减法聚类与模糊c-均值的模糊聚类的研究[J].计算机工程，2005（31）：135-137.XIAO Chunjing，ZHANG Min.Research on fuzzy clustering based on subtractive clustering and fuzzy c-means[J].Computer Engineering，2005（31）：135-137（in Chinese）.

[8]刘坤朋，罗可.改进的模糊C均值聚类算法[J].计算机工程与应用，2009，45（21）：97-98.LIU Kunpeng，LUO Ke.Improved fuzzy c-means clustering algorithm[J].Computer Engineering and Applications，2009，45（21）：97-98（in Chinese）.

[9]温重伟，李荣钧.改进的粒子群优化模糊C均值聚类算法[J].计算机应用研究，2010，27（7）：2520-2522.WEN Chongwei，LI Rongjun.Fuzzy c-means clusteringalgorithm based on improved PSO[J].Application Research of Computers，2010，27（7）：2520-2522（in Chinese）.

[10]刘笛，朱学峰，苏彩红.一种新型的模糊C均值聚类初始化方法[J].计算机仿真，2004，21（11）：148-150 LIU Di，ZHU Xuefeng，SU Caihong.A novel initialization method for fuzzy C-means algorithm[J].Computer Simulation，2004，21（11）：148-150（in Chinese）.

（编辑 李沈）

Research and Application of Pretreatment of Electrical Load Data

SU Zhou，LI Can，YAO Lixiao，CUI Hanjun
（College of Water Resources and Hydropower，Xi’an University of Technology，Xi’an 710048，Shaanxi，China）

The accuracy of the historical load data of the power system is of great importance to the power prediction.In this paper，first，the subtractive clustering algorithm is used to get the number of the clusterings and the cluster centers of the historical load data，which are used at the starting point of the Fuzzy c-means clustering.Second，the lateral similarity of the load curve is used to find out the negative data.Finally，the negative data is corrected using the characteristic curve to get the load data continuously and accurately.The validity of the method is verified through the actual case study.

negative load data；subtractive clustering；fuzzy c-means clustering

2016-12-15。

苏 舟（1993—），女，硕士，主要研究方向为电力系统分析、安全评估与优化运行；

李 灿（1991—），女，硕士，主要研究方向为电力系统分析、安全评估与优化运行；

姚李孝（1963—），男，教授，主要研究方向为电力系统规划与运行。

1674-3814（2017）05-0040-04

TM73

A

国家自然科学基金（51507134）。

Project Supported by the National Natural Science Foundation of China（51507134）.