基于DOM验证蒙提霍尔悖论的设计与实现

高 云

（山西大同大学数学与计算机科学学院,山西大同037009）

基于DOM验证蒙提霍尔悖论的设计与实现

高 云

（山西大同大学数学与计算机科学学院,山西大同037009）

蒙提霍尔悖论自诞生以来,就受到许多博弈论爱好者的不断研究,虽然最终验证了该悖论是成立的,但是研究者给出的论证大多都是深奥难懂的数学公式和推论。为了使大多数读者能够直观的理解该悖论的成立,这里采用了设计直观页面,读者亲自操作,最终通过统计实验数据得出概率的方式来帮助读者对悖论成立的理解。进行该项设计可以采用多种开发工具,而DOM无疑是一个非常适合的选择,它允许程序和脚本动态地访问和更新文档的内容、结构和样式,提供了标准的HTML和XML对象集,并有一个标准的接口来访问并操作它们,使页面的设计实现变得简单方便。

DOM;ECMAScript;蒙提霍尔悖论;算法

蒙提霍尔悖论又叫做三门问题(Monty Hall problem),是一个源自博弈论的数学游戏问题,大致出自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙提·霍尔(Monty Hall)。

蒙提霍尔悖论问世以来,众多的博弈论爱好者对其进行了研究和验证,虽然研究结果最终证明了该悖论的成立,但是深奥的数学公式以及推论过程使得大多数读者很难理解该悖论成立的原因。基于这种情况,本文设计了一种类似于游戏的交互页面,使得读者亲自动手实践,最终使用统计实验数据得出换门后得到正确选择的概率,验证了蒙特霍尔悖论。

1 研究综述

这个游戏的玩法是：参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门就可以赢得该汽车,而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人会开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机会率？如果严格按照上述的条件的话,答案是会—换门的话,赢得汽车的机会率是2/3。

这条问题亦被叫做蒙提霍尔悖论：虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。这问题曾引起一阵热烈的讨论。

Mueser和Granberg透过在主持人的行为身上加上明确的限制条件,提出了对这个问题的一种不含糊的陈述：

·参赛者在三扇门中挑选一扇。他并不知道内里有什么；

·主持人知道每扇门后面有什么；

·主持人必须开启剩下的其中一扇门,并且必须提供换门的机会；

·主持人永远都会挑一扇有山羊的门。如果参赛者挑了一扇有山羊的门,主持人必须挑另一扇有山羊的门；

·如果参赛者挑了一扇有汽车的门,主持人随机在另外两扇门中挑一扇有山羊的门；

·参赛者会被问是否保持他的原来选择,还是转而选择剩下的那一道门；

转换选择可以增加参赛者的机会吗？

问题的答案是可以：当参赛者转向另一扇门而不是继续维持原先的选择时,赢得汽车的机会将会加倍。

有三种可能的情况,全部都有相等的可能性(1/3)：

·参赛者挑山羊一号,主持人挑山羊二号。转换将赢得汽车；

·参赛者挑山羊二号,主持人挑山羊一号。转换将赢得汽车；

·参赛者挑汽车,主持人挑两头山羊的任何一头。转换将失败；

在头两种情况,参赛者可以透过转换选择而赢得汽车。第三种情况是唯一一种参赛者透过保持原来选择而赢的情况。因为三种情况中有两种是透过转换选择而赢的,所以透过转换选择而赢的概率是2/3。在接下来的这个示例中,我们将模仿蒙提霍尔悖论编写如图1所示的页面来验证其理论。

图1 验证蒙特霍尔悖论

设计该页面可以选用很多开发工具,DOM无疑是一个好的选择。文档对象模型(Document Object Model,简称DOM)[1],是W3C组织推荐的处理可扩展置标语言的标准编程接口。DOM是W3C的标准[2],W3C文档对象模型(DOM)是中立于平台和语言的接口,它允许程序和脚本动态地访问和更新文档的内容、结构和样式,提供了标准的HTML和XML对象集,并有一个标准的接口来访问并操作它们。

换句话说,这是表示和处理一个HTML或XML文档的常用方法。有一点DOM很重要[3],DOM的设计是以对象管理组织(OMG)的规约为基础的,因此可以用于任何编程语言。DOM技术使得用户页面可以动态地变化[4],如可以动态地显示或隐藏一个元素,改变它们的属性,增加一个元素等,DOM技术使得页面的交互性大大地增强。DOM的优势主要表现在：易用性强,使用DOM时,将把所有的XML文档信息都存于内存中,并且遍历简单,支持XPath,增强了易用性。

2 验证页面的设计实现

2.1页面功能描述

页面中,放置三张扑克牌,编号依次为0～2号,使用红桃A模拟汽车,使用梅花A模拟山羊。三张牌面中只有一张是红桃A(红色),另外两张为梅花A(黑色),牌面图案如图2所示,参赛者要在三张牌中选中其中的红桃A,即视为赢得比赛。

图2 两种牌面图案

参赛者的游戏操作顺序为首先单击其中的一张牌,我们在选中的牌上加上选中标志,随后程序会翻开一张黑色A,页面如图3所示。

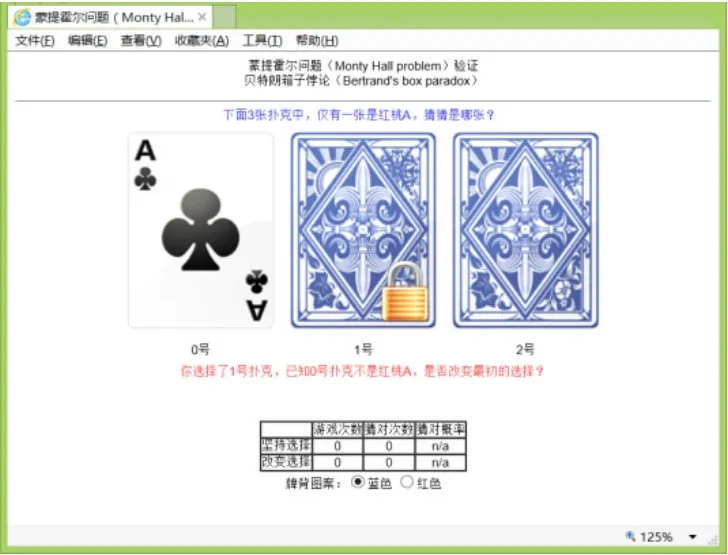
图3 第一次选择后的页面

此时,参赛者有两个选择,维持原来的选取不变或者改为选取另外的一张牌,第二次选取后会亮出全部三张牌的牌面,并提示参赛者是否选取了正确的红桃A。页面下方放置的表格会统计参赛者在是否改变选择的情况下猜对的次数,并计算猜对的概率,以此验证蒙特霍尔悖论是否成立。

2.2页面布局划分

按照图1所示放置页面中的元素,页面大致分为四个部分,依次放置的为辅助信息、游戏操作部分、统计信息和背面图案选择按钮。

2.2.1游戏操作部分

游戏操作部分主要用来放置三张扑克牌及其对应的序号,并提示参赛者应该进行的操作,将扑克牌及其序号使用表格元素放置,在其上方放置如下span元素提示参赛者游戏的内容为“下面3张扑克中,仅有一张是红桃A,猜猜是哪张?”。

〈span〉下面3张扑克中,仅有一张是红桃A,猜猜是哪张?〈/span〉〈span id="cheat"〉〈/span〉

读者会发现,在提示信息的后面还紧跟着另一个id="cheat"的span元素,这是用来放置作弊信息的,即在随机放置三张扑克牌的时候,页面本身是知道红桃A的放置位置的,这里显示红桃A的正确位置,由于是作弊信息,不允许参赛者看到,所以在style元素中将字体颜色设置为白色显示。

读者可以更改其字体颜色,将其显示在页面上。表格划分为2×3的,第一行放置三张扑克牌的背面图片,第二行显示对应的序号。

从图2可以看出,扑克牌背面图片可以有红色和蓝色两种选择,在页面加载时根据单选按钮的选中情况在函数reset()中放置扑克牌背面图片,所以单元格中并没有静态放置图片。单元格的onclick事件会触发函数fn(value),参数value就是当前扑克牌的序号,该函数用来实现游戏的规则。紧挨着扑克牌的下方为id="info"的div元素,提示参赛者在游戏过程中是否改变选择,并在游戏结束后显示游戏结果。

2.2.2统计信息部分

统计信息部分用来统计参赛者是否改变了最初选择、猜对的次数和猜对的概率,由于这里表格中的数据是在游戏过程中根据游戏结果统计得出的,所以页面加载时只放置进行了表格的划分,相应的数据初始化为0和n/a。[5]

2.2.3背面图案选择按钮

页面的最后一部分是选择扑克牌背面图案的单选按钮,为了增加页面的趣味性,可以做红色和蓝色两种选择,其onclick事件代码中给全局变量back赋值,并调用reset()函数根据back的值将扑克牌背面初始化为相应的颜色。可选择的背面图案如图4所示,默认的选择为图例1中的蓝色。

图4 扑克牌背面图案

3 验证算法的设计实现

页面数据处理的操作代码根据需要分别包含在两个函数中,页面加载时调用reset()函数进行元素布局的初始化,游戏过程中点击选中的扑克牌时调用fn()函数进行游戏过程处理和统计数据的给出。代码中需要的全局变量如下所示。

SelFlag表示当前为第几次选择,1表示第一次选择,2表示第二次选择,其余表示一轮游戏结束;firstSel用来记录第一次选择的值,使用第二次选择的值和其进行比较,以判断第二次是否改变了选择;str是将来要显示在id="info"的div元素中的信息,在游戏的不同阶段给出不同的信息;right中放置的是正确选择的序号,该值不只在初始化时可以显示为作弊信息,也是游戏中用于判断选择正确与否的依据;errSel表示进行第一次选取后,页面自动给出的错误选择,0～2分别表示已知的错误为0～2号扑克,-1表示尚未给出(即未进行第一次选择);back值初值为“B”,表示当前扑克牌背面选用的哪种图案,“B”为图4中图例1所示的蓝色,“R”为图4中图例2所示的红色。

3.1元素布局初始化

页面初始化时,首先确定三张扑克牌牌面的放置位置,即将红桃A放置在一个随机位置,另外的两个位置放置黑色牌面,由于一共有三个位置,使用随机函数Math.random()*3选取三个位置中的一个放置红色牌面,并将其位置使用全局变量right记录下来以备后用。此时,页面上将要显示的都是扑克牌的背面图案,并不需要显示红桃A的牌面图案,只需要记录其位置即可。

right=Math.floor(Math.random()*3);//随机放置红桃A,

将获取的正确选择right赋给id="cheat"的span元素,用于作弊显示。

cheat.innerText=right;//显示正确选择(作弊),

id="info"的div元素是在游戏过程中提示参赛者接下来应该进行的操作以及游戏结束后提示结果信息,在游戏开始之前,该元素中没有任何提示信息,将其清空为""。

info.innerHTML="";//清空提示信息。

给相关的标志位赋值,由于接下来的操作为点击扑克牌进行第一次选择,所以将记录第几次选择的全局变量SelFlag赋值为1用于第一次选择的判断。在没有进行第一次选择扑克牌之前,是不会给出已知错误的扑克牌的,即游戏开始之前,errSel的值为-1,表示尚未给出已知错误的扑克牌。

SelFlag=1;//选择标志：1表示第一次选择,2表示第二次选择,其余表示一轮游戏结束，

errSel=-1;//自动给出的错误选择：0～2分别表示已知的错误为0～2号扑克,-1表示尚未给出(即未进行第一次选择)，

最后,将扑克牌背面图片放置在id="imgi"的img元素中,扑克牌的牌面图案不一样,背面图案初始时却是相同的,初始时img元素放置的是相同的背面图案,当点击扑克牌进行选择后,才会显示牌面图案和不一样的背面图案。使用循环依次放置三张扑克牌的背面图案,循环变量i在这里也用于确定img元素的id值,即img元素的id值为"img"和i组合而成,我们调用的ECMAScript的eval()方法来完成这一功能,eval(string)函数可计算某个字符串,执行其中的ECMAScript代码,并返回通过解释参数string得到的值。eval()的功能非常强大,将"img"+i作为其参数,可以返回img元素正确的id值。

给其src属性赋值为相应的图片,图片有两种(颜 色 不 同),名 称 分 别 为“m_backB.png”和“m_backR.png”,其名称中不一样的部分恰好是存放在全局变量back中的值,所以放置的图片的完整名称为"m_back"+back+".png"。当图片显示为扑克牌背面图案时,鼠标在图片上的形状为手型,当图片显示为扑克牌牌面图案时,鼠标在图片上的形状为缺省形状,即指针形状。游戏开始之前,所有的图片都显示为背面图案,此时,鼠标指针为手型。

for(var i=0;i〈=2;i++){//初始化或恢复图片为未知状态,鼠标指针为手型，

函数reset()完整的代码如下所示。SelFlag=1;//选择标志：1表示第一次选择,2表示第二次选择,其余表示一轮游戏结束，

errSel=-1;//自动给出的错误选择：0～2分别表示已知的错误为0～2号扑克,-1表示尚未给出(即未进行第一次选择)，

3.2游戏过程处理和统计数据的给出

参赛者在游戏过程中要做的就是选取不同位置的扑克牌,点击扑克牌会触发img对象的onclick事件,调用fn(value)函数,参数value表示的是被点击的扑克牌的序号。将参赛者点击扑克牌的操作分为三种情况加以处理,第一种为游戏没有结束,而参赛者点击了已经显示了牌面的扑克牌,即当前触发事件的序号value等于已经给出的错误序号err-Sel,或者是游戏已经结束了,所有的扑克牌都已经显示了牌面,此时,参赛者又点击了扑克牌,即参赛者选择的次数SelFlag已经大于2次,这种情况我们会认为是参赛者进行了误操作,不做任何处理,直接退出函数即可。

if(value==errSel||SelFlag〉 2)return;//点击了已经给出的错误选择或一轮游戏已经结束；

第二种情况为,参赛者第一次选择了牌面未知的扑克牌,此时,函数应该首先将该扑克牌背面图案变为已选定状态的背面图案,选中状态的扑克牌背面图案如图5所示。

eval("img"+value).src="m_backSel"+back+".png";//显示已选择的扑克背面(包含锁)。

图5 选中状态的扑克牌背面图案

根据已选的序号给出一个已知错误的序号,如果已选中的序号为恰好为红桃A的序号,即正确的序号,那么已知错误的序号就在另外两个中随机选取一个,选取的方法为给原有的序号加上1或者2之后再模3;如果选中的序号为一个错误的序号(黑色牌面),那么将另外一个错误的序号给出,三张牌的序号之和为0+1+2等于3,要给出的已知错误序号为3减去正确的序号,再减去选中的错误的序号,将获取的要给出的错误序号赋给errSel。

给出已知错误序号之后,要将相应位置上的扑克牌显示为黑色牌面,并将该图片上的鼠标指针设置为默认形状。

最后,设置相应的标志和提示信息,将第一次选取的序号保留下来以便和第二次选取的序号做对比判断是否改变了选择,选取次数加1,设置提示信息,提示参赛者当次选取的序号、已知错误牌面的序号和是否要改变选择。

firstSel=value;//记录第一次选择的值,以判断第二次是否改变了选择，

info.innerHTML="你选择了"+value+"号扑克,已知"+errSel+"号扑克不是红桃A,是否改变最初的选择？"

SelFlag++;//第一次选择完成,修改标志，

第一次选择后页面如图3所示(以蓝色背面为例)。

第三种情况为参赛者进行了第二次选择,首先要做的工作是,不管选择结果是否正确,都会全部显示三张牌的牌面,使用循环依次判断序号i是否等于right,正确的序号显示的是红桃A的牌面(m_heartA.png),错误的序号显示的是梅花A的牌面(m_clubA.png),并将三张牌的鼠标指针都恢复为默认状态,这里仍然使用eval()方法获取img元素的id值。

接下来判断第二次是否改变了选择,使用不同的情况下的统计数据来填写页面最下方的表格,放置坚持选择时获取的数据的单元格的id值为"l0"～"l2",放置改变选择时获取的数据的单元格的id值为“h0”～“h2”,为了不重复进行相同的工作,使用变量t来放置单元格id值的第一个字符,再使用方法eval(t+x)返回完整的id值。第一个单元格“t0”放置每种情况下游戏的总次数,计算方法为将上一次单元格中的数字加1。

如果参赛者猜对了正确的序号,将“t1”单元格中猜对的数字加1,并且在提示信息中显示“很幸运,你猜对了！”,为了增加游戏的趣味性,如果参赛者没有改变选择,提示信息中增加“矢志不渝！”,如果参赛者改变了选择,提示信息中增加“通权达变！”。如果参赛者选择了错误的序号,提示信息为“很遗憾,你猜错了！”,判断是否改变了选择在提示信息中增加的内容分别为“执迷不悟！”和“朝秦暮楚！”。由于〈div id="info"〉元素中在后面的代码还会增加其他信息,这里使用的变量str暂存上述信息。

str="很遗憾,你猜错了！"+(firstSel==value?"执迷不悟！"："朝秦暮楚！");

最后,根据猜对的次数统计猜对概率,将其写入“t2”单元格中。使用猜对次数/游戏次数,即为猜对概率,我们使用百分比的形式显示概率,即需要将除法结果扩大100倍,由于百分比结果要保留2位小数,所以将除法结果扩大10000倍后取整,再除以100就是最后猜对的概率。

eval(t+2).innerText=Math.round(parseInt(eval(t+1).innerText)/parseInt(eval(t+0).innerText)*

10000)/100+"%";//统计猜对概率(保留2位小数)。

在〈div id="info"〉元素中显示变量str中的内容,并且添加按钮元素,点击进行下一次游戏,按钮value值为“再猜一次”,点击按钮调用函数reset(),初始化页面开始新游戏。设置标志变量SelFlag++,表示第二次选择完成。

4 测试结果

页面加载后,请读者耐心进行游戏,会发现,进行游戏的次数足够多时,坚持选择时猜对的概率为33.33%(1/3),改变选择时猜对的概率为66.66%(2/3),验证了蒙特霍尔悖论。

[1]刘德山,杨彬彬.HTML+CSS+JavaScript网站开发实用技术[M].北京：人民邮电出版社,2014.

[2]莫卓颖.基于语义DOM的WEB信息抽取[D].桂林：广西师范大学,2012.

[3]马瑞民,钱浩.基于时间频率加权DOM的Web信息抽取方法[J].长江大学学报(自然科学版),2011(1)：59-61.

[4]李大成,陈莘萌.Java与XML的结合应用[J].计算机应用,2002(2)：5-9.

[5]廉捷,刘云.网络舆情中的信息预处理与自动摘要算法[J].北京交通大学学报,2010(5)：94-99.

Design and Implementation of Validation Monty Hall Problem Based on DOM

GAO Yun
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

Since the appearence of Monty Hall problem,it has been studied by many game enthusiasts.Although it was finally verified as true,most explanations are esoteric mathematical formula and inference.In order to enable most readers to understand the establishment of the paradox,this paper tries to design intuitive web page in which readers can operate in person and get the probability by statistical experimental data.A variety of development tools can be used for the design.Among them DOM is a good choice,which allows access to programs and scripts and update of content,structure and style of the document,provides a standard set of HTML,XML objects,and a standard interface for accessing and manipulating them,making page design easy and convenient.

DOM;ECMAScript;Monty Hall problem;algorithm

TP393.092.2

A

〔责任编辑 高海〕

1674-0874(2017)01-0001-06

2016-11-08

高云(1976-),女,山西大同人,硕士,讲师,研究方向：计算机网络应用。