考虑噪声源深度分布的海洋环境噪声模型及地声参数反演∗

江鹏飞 林建恒2)† 孙军平 衣雪娟

1)(中国科学院声学研究所北海研究站,青岛 266023)2)(中国科学院水声环境特性重点实验室,北京 100190)(2016年7月13日收到;2016年10月11日收到修改稿)

考虑噪声源深度分布的海洋环境噪声模型及地声参数反演∗

江鹏飞1)林建恒1)2)†孙军平1)衣雪娟1)

1)(中国科学院声学研究所北海研究站,青岛 266023)2)(中国科学院水声环境特性重点实验室,北京 100190)(2016年7月13日收到;2016年10月11日收到修改稿)

考虑到海洋环境噪声源深度分布不集中,建立了噪声源随深度分布的海洋环境噪声模型,分析了源深度对噪声场垂向特征的影响并从简正波角度予以解释,发现海底声阻抗和声源深度都显著影响由海洋环境噪声获得的等效海底反射损失大掠射角部分,进而将该模型用于地声参数反演.两段实测噪声数据200—525 Hz频段的反演结果表明:基于海洋环境噪声的地声参数反演最优值与声传播的反演结果相近;源平均深度最优值随频率增加有变小的趋势,说明随频率增加环境噪声主要贡献源逐渐由航船转为风浪;当海况大于3级时,400 Hz以上频段噪声源深度平均值很小,与Monahan气泡理论的描述一致.

环境噪声源,深度分布,地声反演

1引 言

海洋环境噪声在几十赫兹至20kHz段内有两种主要的噪声源[1]:风关噪声和远处航船噪声.航船噪声是200 Hz以下的主要噪声源,风关噪声是1kHz以上的主要噪声源,而在200 Hz至1kHz频段内,航船噪声与风关噪声都有贡献,所占比例取决于航运繁忙程度和海况.众所周知,气泡是风关噪声的主要噪声源,波浪破碎将空气卷入海水中,形成气泡,基于大量的实验观测和前人的工作,Monahan[2]系统阐述了气泡的演变历程,当风速达到5.4m/s时(3级海况)且持续作用时,海浪破碎在海面产生白沫,白沫以下临近海面处会持续生成大量气泡,当风力较弱时,破碎波浪产生向下喷射的动力消散,气泡经过一系列演变最终与白沫分离,和背景气泡层融为一体,分布于较大的深度范围内,在11—13m/s风速作用下,气泡最大深度可达10米,密度最大值出现在4m处[3];而作为高工况航船噪声主要来源的螺旋桨一般位于水面下几米至十几米的深度,可见“混合”噪声源的存在可导致环境噪声源深度分布较分散.那么在某些频段声场预报和地声参数反演中,继续使用假设噪声源随机连续分布在接近海面的同一无限大平面上的传统环境噪声模型,显然不够合理,可导致预报或反演结果出现较大误差.本文讨论了噪声源深度对环境噪声场垂向空间特征的影响,并给出合理的物理解释,进而将噪声源深度分布的环境噪声模型用于地声参数反演.

有关海洋环境噪声模型,最早可追溯到1962年,Cron和Sherman[4]把深海看作一个均匀的半空间,假设噪声源指向性为cospθ,建立了一个深海环境噪声模型.1972年,Cox[5]将空间相关性分析运用在噪声场研究中,加入波数谱概念,建立了海洋环境噪声模型.1980年,Kuperman和Ingenitgo[6]提出了K-I模型,认为噪声源随机连续分布于接近海面的无穷大平面上,利用波动理论推导了分层海洋中噪声场空间相关函数.Buckingham和Carbone[7]推导了适用于半无限海洋的两点间环境噪声空间相关公式,分析了噪声源深度对环境噪声空间相关的影响,指出随着噪声源深度增加,噪声源偶极子特征变弱,导致噪声场空间相关系数逐渐与频率无关.何利[8]考虑噪声源深度分布,改进了K-I噪声模型并计算了海洋环境噪声场垂直相关,很好地解释了试验现象.

此外,近年来利用环境噪声反演地声参数,由于其不需要发射声源,易于实施等优点逐渐受到人们的青睐.Deane等[9]分析了海底声速和衰减对海洋环境噪声垂直指向性和垂直相关的影响,并利用海洋环境噪声垂直相关反演了声速等海底参数.Aredov和Furduev[10]通过测量噪声场的垂向能量分布,等效转化成海底反射损失,理论分析了由噪声场提取海底反射系数的可能性.Arvelo[11]分析了东中国海环境噪声试验数据,针对海水衰减、阵倾斜、近场船只等参数失配条件,分析了噪声反演的稳健性和限制条件.Quijano等[12]将贝叶斯匹配场处理方法用于风关环境噪声反演,并指出风速是影响反演结果的重要因素.骆文于[13]利用中美联合考察东中国海得到的噪声数据,反演得到无限大液态半空间海底声速、密度、衰减.李丙辉[14]建立了海洋环境噪声简正波模型,反演了分层海底声学参数,仅有仿真结果,未涉及试验数据.殷宝友等[15]利用三个参数表征海底反射,建立了海底简化的海洋环境噪声模型,并用来反演海底声学参数,该方法不考虑海底分层结构,相对简单.此外江鹏飞等[16]针对海底密度不敏感问题,提出了分步反演策略.

以上回顾了部分海洋环境噪声建模及反演海底参数的理论及试验结果,不难发现,人们只讨论了噪声源深度对环境噪声场空间相关特性的影响,并未涉及噪声场其他空间特征,也没有将噪声源深度分布的环境噪声模型用于地声参数的反演.本文首先考虑噪声源的深度,修改了基于射线法的近场环境噪声模型,建立了噪声源深度分布的海洋环境噪声模型;然后讨论噪声源深度对环境噪声垂直阵响应的影响,并给出合理的物理解释;接下来基于噪声源深度分布海洋环境噪声模型,利用不同海况下的实测海洋环境噪声数据来反演地声参数,并对反演结果进行分析;最终得出结论.

2噪声源深度分布的海洋环境噪声模型

本文海洋环境噪声模型采用近场射线法、远场简正波法混合算法.

射线法计算环境噪声近场特性:N元等间距垂直水听器阵布放于水中,相邻水听器间距为Δ,噪声源深度为zs时,其中任意两个水听器接收环境噪声互谱密度表示为[17]

其中q为噪声源强度,θ′为m,n水听器对的仰角(−π/2 ＜ θ′＜ 0为海面方向),kmn=2πf/cmn,cmn为两个水听器中心位置声速,不同角度幅度因子A(θ′,f)表示为

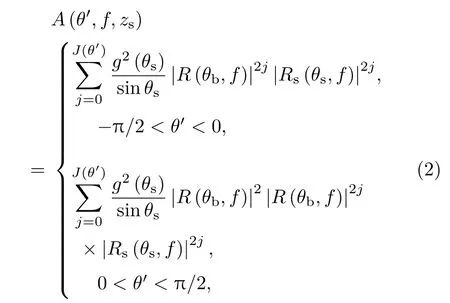
其中Rs(θs,f),R(θb,f)分别为海面、 海底的反 射 系 数, θs= cos−1(cos(θ′)cs/cmn), θb=cos−1(cos(θ′)cb/cmn),cs,cb分别为海水中海面、海底位置声速,这里假设 Rs(θs,f)=1;J(θ′)为近场完整声线循环次数,可借助射线传播程序求得;g(θs)是噪声源的指向性函数,通常考虑噪声源深度较小,假设声源为偶极子,令g(θs)=sinθs,而随着噪声源深度增加,噪声源偶极子特性逐渐消失,本文为讨论噪声源深度zs对环境噪声场的影响[18],图1给出zs=2m、频率300 Hz情况下两种噪声源的指向性比较,二者差别明显.

于是,近场环境噪声垂直阵响应可以表示为

图1 声源深度2m、频率300 Hz两种噪声源指向性比较Fig.1.zs=2m,f=300 Hz,the comparison between two kinds of noise source directionality.

简正波法计算环境噪声远场特性:

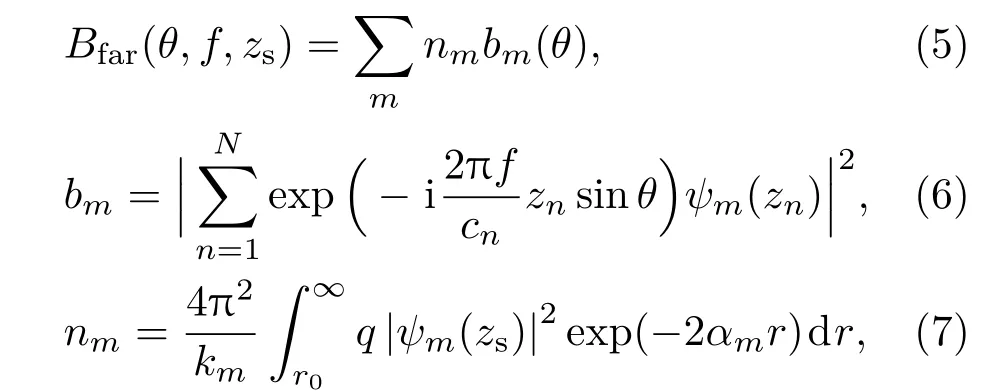
其中ψm为第m号简正波本征函数,km为简正波本征值,αm为其虚部,r0为近场距离,本文记作r0=10×D,D为海深.

那么噪声源深度为zs时环境噪声垂直阵响应可表示为

Bz(θ,f,zs)=Bnear(θ,f,zs)+Bfar(θ,f,zs).(8)

本文假设噪声源密度随深度服从高斯分布:

其中z0为均值,σ2为方差.则环境噪声垂直阵响应表示为

根据Harrison的理论[19],可通过环境噪声垂直阵响应获得等效海底反射损失:

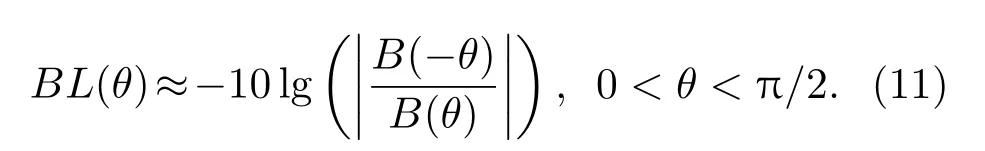
本文模型在计算近场环境噪声时对射线法进行了修改,使其能够适应噪声源深度变化的情况.为验证本文近场模型,将其和采用scooter程序的近场波数积分模型[16]的计算结果进行比较,仿真环境如表1所列,假设相邻阵元间距1m的31元垂直接收阵位于海水层中心位置.图1和图2分别给出了频率450 Hz声源深度分别为0.1m,2m时两个模型的计算结果.就近场计算结果而言,二者在大仰角部分基本一致,在0°附近二者存在一定差距,原因是对于小仰角,(2)式中J(θ′)的微小差别可导致计算范围的较大出入,但是从总声场计算结果来看,二者在小仰角的差别可忽略不计.

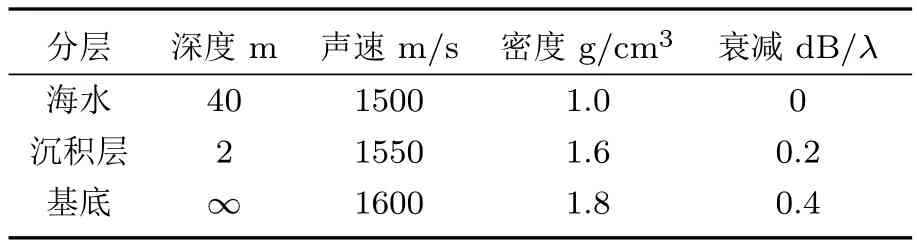
表1 仿真环境参数Table 1.Environment parameters of simulation.

图2 (网刊彩色)两种模型计算环境噪声垂直阵响应比较 (a)声源深度zs=0.1m;(b)zs=2mFig.2.(color online)The vertical array response of ambient noise calculated by two models:(a)Source depth zs=0.1m;(b)zs=2m.

3噪声源深度的分析和讨论

本节借助上述模型仿真计算噪声源不同深度时海洋环境噪声垂向特征,并从简正波角度给出合理的解释,进而分析不同地声参数对垂向特征的敏感度,以便利用环境噪声反演地声参数.

3.1 声源深度对环境噪声场垂向特征的影响

仿真环境同表1,海底反射系数[20]可表示为

其中Zj=ρjcj/sinθj,j=1,2,3,分别代表海水、沉积层和基底;c,ρ,θ分别是声速、密度和掠射角.考虑到海底衰减,声速通常表示为复数形式:其中α为衰减系数,单位为为沉积层厚度.那么海底损失为

分别计算噪声源位于不同深度时250,450 Hz海洋环境噪声垂直阵响应和等效反射损失,结果如图3和图4所示.可见随着噪声源深度的改变,海洋环境噪声垂直阵响应能量大小、近场形状都有明显变化.简正波理论认为,噪声源激发各号简正波强度可表示[21]为2

与噪声源深度处本征函数成正比.图5给出了250,450 Hz前5号简正波本征函数,随着噪声源深度由海面逐渐下移,声源激发的各号简正波能量增强,环境噪声垂直阵响应值也变大了.

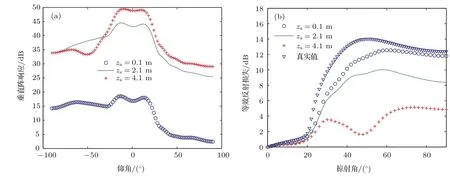
图3 (网刊彩色)噪声源深度不同时250 Hz (a)环境噪声垂直阵响应;(b)等效海底反射损失Fig.3.(color online)(a)The vertical array response,(b)equivalent seabed re fl ection loss of 250 Hz ambient noise when the source depth is di ff erent.

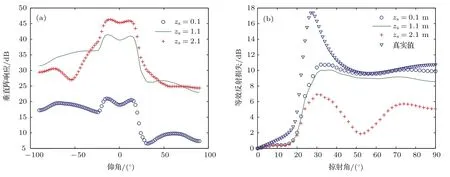
图4 (网刊彩色)噪声源深度不同时450 Hz(a)环境噪声垂直阵响应,(b)等效海底反射损失Fig.4.(color online)(a)The vertical array response,(b)equivalent seabed re fl ection loss of 450 Hz ambient noise when the source depth is di ff erent.

图5 不同频率前5号简正波本征函数Fig.5.The eigenfunctions of fi rst fi ve normal modes of di ff erent frequencies.

噪声源深度变化还显著改变了环境噪声垂直阵响应凹槽外侧部分的形状(以及大掠射角的等效海底反射损失),为解释这一现象,先讨论不同简正波对大掠射角等效海底反射损失的作用.可采用(1)—(4)式和(9)式仿真计算,这里假设(2)式中

图6 不同简正波作用下的AFig.6.The Awith di ff erent normal modes.

来分别对应高号、低号简正波,那么分别求得A(θ′,f,zs)、大掠射角等效海底反射损失,结果如图6和图7所示.可见只有高号简正波作用时,等效海底反射损失大掠射角部分远高于低号简正波作用的结果,高号简正波“抬高”了等效海底反射损失.主要原因在于与高号简正波对应的大掠射角声线与海底碰撞时,海底反射损失较大,从而导致海面、海底方向传来的声线能量差异明显.噪声源深度增大到一定程度,其激发的高号简正波能量开始衰减,而低号简正波能量持续增强,由此便可解释为什么随着噪声源深度增加,等效海底反射损失大掠射角部分降低了.

图7 不同简正波作用下的等效海底反射损失Fig.7.The equivalent seabed re fl ection loss with different normal modes.

另外,由图3(b)和图4(b)不难发现以下两个现象:1)由于海面噪声源激发的高号简正波能量强于低号简正波,噪声源深度越接近海面,等效海底反射损失越大、越接近真实值,尤其在大角度部分;2)由于频率越高,噪声源声源激发各号简正波强度随深度变化越快,当噪声源深度由0.1m变为2.1m时,450 Hz环境噪声垂直阵响应获得的等效海底反射损失的变化大于250 Hz.

3.2 海底声学参数敏感度分析

图8 海底参数对环境噪声垂直阵响应和等效海底反射损失的敏感性曲线 (a)声速;(b)密度;(c)衰减Fig.8.The curve of the sensitivity of seabed parameters to the vertical array response of ambient noise and equivalent seabed re fl ection loss:(a)Sound speed;(b)density;(c)attenuation.

图8分别给出了海底声速、密度以及衰减系数对200 Hz环境噪声垂直阵响应和等效海底反射损失的敏感性曲线,图中每条曲线标注的两个数字分别为沉积层和基底参数.可见,不同海底参数对海洋环境噪声场垂向特征敏感度不同,海底声速是在所有掠射角下对海底反射损失都有影响的重要参数;在大掠射角入射时,海底损失主要由法向声阻抗率决定,海底密度很重要,但对于小于临界角的掠射角,其对海底反射损失的影响基本可以忽略;衰减系数在掠射角小于临界角时对海底反射损失影响较大.

综上所述,海底声速、密度和声源深度都显著影响等效海底反射损失大掠射角部分,如果依然假设噪声源随机连续分布于接近海面的无穷大平面上,难免出现海底声速、密度反演结果偏大的情况,而简单地假设噪声源位于水下某一深度显然与实际情况不符,采用噪声源随深度分布的海洋环境噪声模型作为地声参数反演的正向模型,可有效减少反演误差.

4噪声试验分析及海底参数反演

声源深度对海洋环境噪声垂向特征影响显著,反演过程中若声源深度处置不当,可导致反演结果出现较大误差.本节将噪声源深度分布的海洋环境噪声模型作为正向模型,利用某次海试测量的环境噪声数据来提取地声参数.

4.1 噪声试验过程

试验选在某海域浅水区,平均海深约为37m,海底地形比较平坦,浅剖显示海底无明显分层,平均声速剖面如图9所示,10—15m范围内有较强的跃层.在声传播试验间隙,利用自容式的水听器垂直线列阵采集噪声数据,垂直阵布放于2—30m深度,相邻阵元间距为1m,这里选取两段时长约为2min噪声数据进行处理,两段数据采集过程中平均风速分别为2.8,4.86m/s(换算成海面10m处风速分别约为3.1,6.1m/s).图10给出了两段不同深度环境噪声功率谱数据,具有较为明显的航船噪声特征:低频谱峰附近出现一系列谐波线谱.此外,由于风速较大,数据2的风关噪声环境噪声(大于200 Hz频段)功率谱要明显高于数据1.图11给出了两段环境噪声垂直阵响应数据可见:1)除±20°外,在约负20°到负90°方向上能量较强且出现其他峰值,说明附近确实有船只;2)在低频段0°附近未见“凹槽”,可能由远处航船所致.

4.2 反演方法

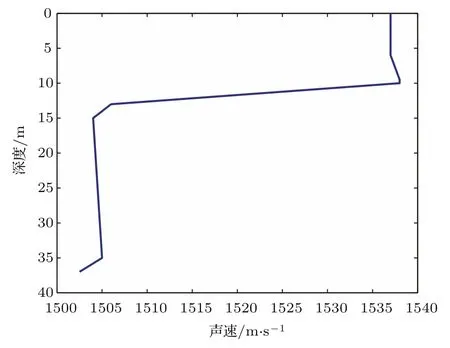
图9 试验期间平均声速剖面Fig.9.The mean sound speed pro fi le during the experiment.

图10 (网刊彩色)不同深度环境噪声功率谱Fig.10.(color online)The spectrum of ambient noise at various depths.

图11 两段数据环境噪声垂直阵响应随频率变化Fig.11.The change of vertical array response of ambient noise with di ff erent frequencies.

下面扼要介绍海底声学参数的反演方法,假设海底为无限大半空间,待反演的参数为m={c,ρ,α,σ2,z1,z2,···,zn},其中c,ρ,α分别为海底声速、密度、衰减系数,σ2为噪声源随深度高斯分布的方差,zn为不同频率源深度均值.采用等效海底损失理论值BLinv与试验值BLexp的均方差为代价函数进行多频联合反演:

其中Ntheta为角度个数.本文选择在匹配场反演中广泛应用的自适应单纯形模拟退火算法[22]实现待反演参数最优值求解.自适应模拟退火算法结合模拟退火和单纯形下降法两种方法的优点,具有很强的全局优化搜索能力,速度快,鲁棒性较好.

4.3 反演结果分析

表2给出了待反演参数及其搜索范围和同次试验中利用声传播、环境噪声反演的结果,可见将噪声源深度分布的环境噪声模型用于反演时,由两段数据提取的地声参数结果相近,与声传播反演结果差别较小,分析海底底质介于第6,7类[23]之间.传统模型反演(假设声源深度为0.1m)获得的地声参数均大于声传播反演结果,其中密度最优值远高于经验值.通过分析由两段数据获取的不同频率声源深度均值,可以发现频率高于400 Hz时,噪声源平均深度最优值明显小于低频段的反演结果,主要原因在于随频率的增加,海洋环境噪声主要贡献源逐渐由航船转为风浪,这也符合Wenz曲线的特征.此外,由数据2获取的425 Hz和500 Hz源平均深度最优值很小,远小于数据1,这可根据Monahan的理论予以解释:当风速大于5.4m/s时,海面波浪破碎,临近海面处持续生成大量气泡,从而使高于400 Hz频段噪声源多集中于海面下极小深度内;当风速较小时,风关噪声主要噪声源为背景气泡层,噪声源深度分布较分散.数据2获取的525 Hz源平均深度最优值为2.5m,与上述理论不符,原因可能是该频率位于航船噪声干涉结构的谱峰附近.图12和图13分别给出数据1,2待反演参数随迭代次数的变化,随着迭代次数的增加,待反演参数逐渐趋于最优值.图14和图15分别给出两组数据反演最优值代入模型计算等效反射损失与实测值的比较,可见大多数频率在大掠射角部分二者符合较好,频率大于300 Hz时,实测值在掠射角小于60°的部分出现起伏,而模型计算结果相对平稳,原因在于:实验期间某一深度或某几个深度存在较强噪声源,可导致等效反射损失实测值出现起伏,而模型计算结果相当于一定深度范围内的所有深度计算值加权平均,所以结果相对平稳.

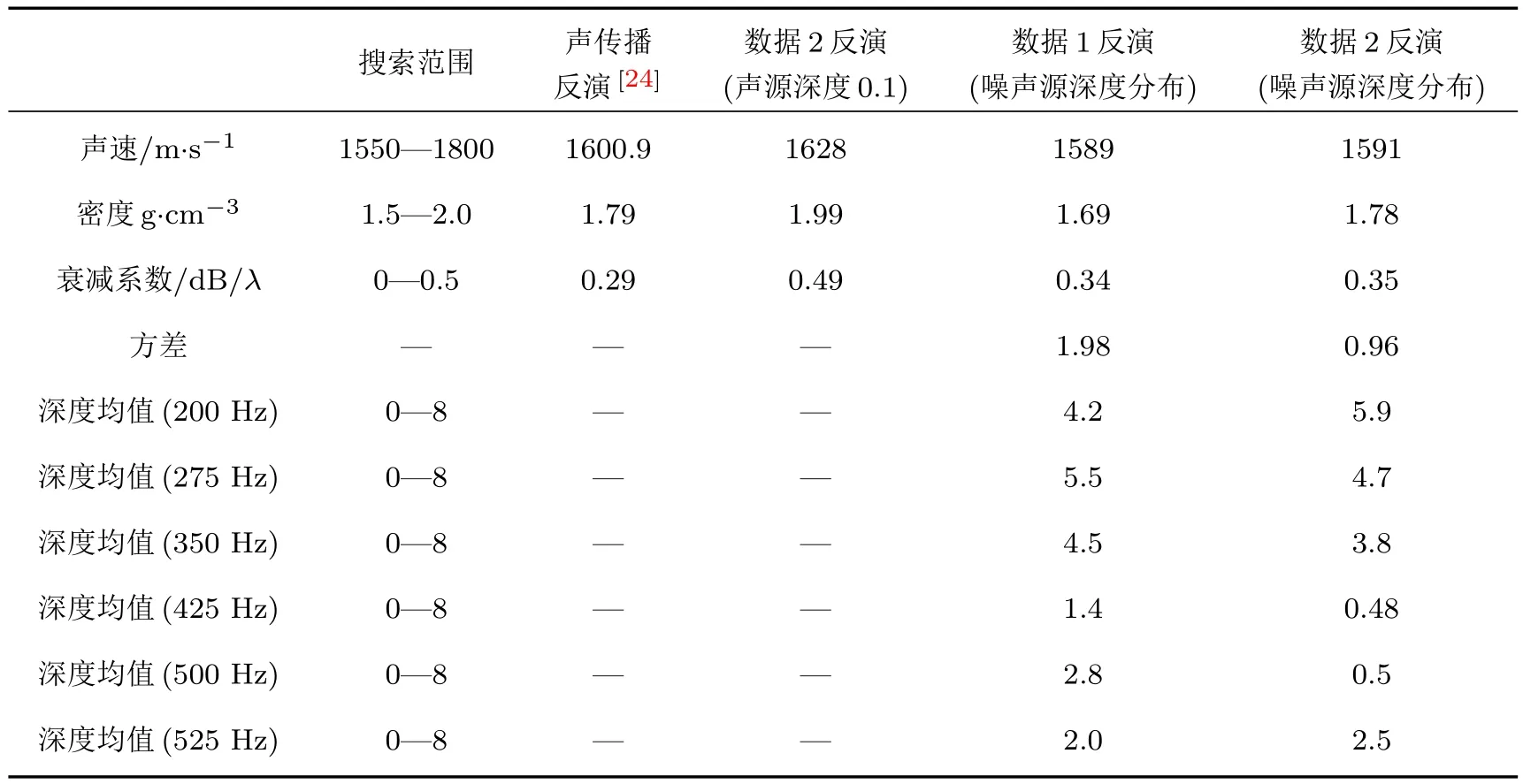
表2 待反演参数及反演结果信息表Table 2.The range of parameters for inversion and the inversion results.

图12 待反演参数随迭代次数变化(数据1)Fig.12.The value change of parameters for inversion with number of iteration(data 1).

图13 待反演参数随迭代次数变化(数据2)Fig.13.The value change of parameters for inversion with number of iteration(data 2).

图14 实测结果与反演最优值计算结果比较(数据1)Fig.14.The experimental results compared to the predicted results evaluated at inverted value(data 1).

5结 论

在200—2kHz频段内,航船及风浪是环境噪声的两种主要声源,“混合”声源的存在使该频段环境噪声源深度分布较分散.这种情况下,海洋环境噪声建模如果依然沿用噪声源均匀分布在接近海面的无限大平面上的假设,显然是不合适的,为此本文建立了噪声源深度分布的海洋环境噪声模型,并将该模型用于地声参数反演.本文主要结论如下.

1)噪声源深度对等效海底反射损失大掠射角部分(环境噪声垂直阵响应凹槽外侧部分)的形状影响显著,主要原因在于:不同号简正波对等效海底反射损失大掠射角部分作用不同.与高号简正波对应的大掠射角声线与海底碰撞时,海底反射损失较大,使海面、海底方向传来的声线能量差异明显,所以高号简正波可“抬高”等效海底反射损失.那么,随着噪声源深度在一定范围内增大,激发的低号简正波能量持续增强,而高号简正波较早出现衰减,从而导致等效海底反射损失变小.

2)海底声速、密度和声源深度共同决定等效海底反射损失大掠射角部分,地声参数反演中需将声源深度考虑在内.

图15 实测结果与反演最优值计算结果比较(数据2)Fig.15.The experimental results compared to the predicted results evaluated at inverted value(data 2).

3)实测数据反演结果表明,利用环境噪声反演的地声参数与声传播的反演结果相差较小,且与经验值相符;随着频率增加,源平均深度反演最优值有变小的趋势,表明环境噪声主要贡献源逐渐由航船转为风浪,这符合Wenz曲线对噪声源特征的描述;当风速大于5.4m/s时,风关噪声源(＞400 Hz)集中于海面下很小的范围内,而风速较小时,风关噪声源(＞400 Hz)深度分布较分散,这与Monahan气泡理论相符合.

[1]Wenz G M 1962 J.Acoust.Soc.Am.34 1936

[2]Monahan E C 1988 Sea Surface Sound:Natural Mechanisms of Surface Generated Noise in the Ocean(Dordrecht:Kluwer Academic Publisher)p85

[3]Kolovayev D A 1976 Oceanology 15 659

[4]Cron B F,Sherman C H 1962 J.Acoust.Soc.Am.34 1732

[5]Cox H 1973 J.Acoust.Soc.Am.54 1289

[6]Kuperman W A,Ingenito F 1980 J.Acoust.Soc.Am.67 1988

[7]Buckingham M J,Carbone N M 1997 J.Acoust.Soc.Am.102 2637

[8]He L 2007 Ph.D.Dissertation(Beijing:Institute of Acoustics,Chinese Academy of Sciences)(in Chinese)[何利2007博士学位论文(北京:中国科学院声学研究所)]

[9]Deane G B,Buckingham M J,Tindle C T 1998 J.Acoust.Soc.Am.103 801

[10]Aredov A A,Furduev A V 1994 Acoust.Phys 40 176

[11]Arvelo J I 2008 J.Acoust.Soc.Am.123 679

[12]Quijano J E,Dosso S E,Dettmer J,Zurk L M,Siderius M 2012 J.Acoust.Soc.Am.131 2659

[13]Luo W Y 2002 Ph.D.Dissertation(Beijing:Institute of Acoustics,Chinese Academy of Sciences)(in Chinese)[骆文于 2002博士学位论文 (北京:中国科学院声学研究所)]

[14]Li B H 2004 M.S.Thesis(Qingdao:Ocean University of China)(in Chinese)[李丙辉2002硕士学位论文(青岛:中国海洋大学)]

[15]Yin B Y,Ma L,Lin J H 2012 Acta Acoust.37 424(in Chinese)[殷宝友,马力,林建恒 2012声学学报 37 424]

[16]Jiang P F,Lin J H,Ma L,Yin B Y,Jiang G J 2016 Acta Acoust.41 56(in Chinese)[江鹏飞,林建恒,马力,殷宝友,蒋国健2016声学学报41 56]

[17]Harrison C H 1997 Appl.Acoust.51 289

[18]Jesen F B,Kuperman W A,Porter M B,Schmidt H,2011 Computional Ocean Acoustics(New York:Springer-Verlag)pp17–18

[19]Harrison C H,Simons D G 2002 J.Acoust.Soc.Am.112 1377

[20]Jesen F B,Kuperman W A,Porter M B,Schmidt H,2011 Computional Ocean Acoustics(New York:Springer-Verlag)pp46–47

[21]Duda T F,Preisig J C 1999 IEEE J.Oceanic Eng.24 16

[22]Dosso S E,Wilmut M J,Lapinski A S 2001 IEEE J Oceanic Eng.21 324

[23]Hamilton E L 1980 J.Acoust.Soc.Am.68 1313

[24]Lu L C,Ma L 2008 Tech Acoust.27 56(in Chinese)[鹿力成,马力2008声学技术27 56]

PACS:43.30.Nb,43.30.PcDOI:10.7498/aps.66.014306

*Project supported by the National Natural Science Foundation of China(Grant No.11174314),and the Open-end Funds of the Key Laboratory of 715th Research Institute China Shipbuilding Industry Corporation(Grant No.KF201502).

†Corresponding author.E-mail:linjh@mail.ioa.ac.cn

Ocean ambient noise model considering depth distribution of source and geo-acoustic inversion∗

Jiang Peng-Fei1)Lin Jian-Heng1)2)†Sun Jun-Ping1)Yi Xue-Juan1)

1)(Qingdao Branch,Institute of Acoustics,Chinese Academy of Sciences,Qingdao 266023,China)2)(Key Laboratory of Underwater Acoustic Environment,Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China)(Received 13 July 2016;revised manuscript received 11 October 2016)

An ocean ambient noise model is established considering source depth distribution.The model is used to analyze the e ff ect of source depth on the vertical characteristics of ambient noise fi eld.The analyses are explained and validated by normal mode theory.The energy of normal mode excited changes with source depth.E ff ects of di ff erent order normal modes are di ff erent.The high order modes raise up the equivalent seabed re fl ection loss,whereas the low order modes depress it.It is found that the seabed sound speed,density and source depth all have signi fi cant in fl uences on equivalent seabed re fl ection loss at large grazing angles.So the source depth should be taken into account and the model is used in geo-acoustic inversion.Two sets of experimental data in a bandwidth of 200—525 Hz are used to obtain geo-acoustic parameters.The results show that the geo-acoustic parameters inverted from ocean ambient noise and from sound propagation data are similar.The mean value of inverted source depth tends to be smaller as frequency increases,which demonstrates that wind waves become dominant over ship noise.The average of inverted source depth values in the band(＞400 Hz)is very small when sea state is higher than grade 3,which is consistent with the result from the Monahan’s bubble theory.

ambient noise source,depth distribution,geo-acoustics inversion

10.7498/aps.66.014306

∗国家自然科学基金(批准号:11174314)和中船重工715所重点实验室开放基金(合同号:KF201502)资助的课题.

†通信作者.E-mail:linjh@mail.ioa.ac.cn