非球形效应对强声场中次Bjerknes力的影响∗

马艳1)2) 林书玉1)† 徐洁1) 唐一璠1)

1)(陕西师范大学陕西省超声学重点实验室,西安 710062)2)(宁夏师范学院物理与电子信息工程学院,纳米结构及功能材料工程技术研究中心,固原 756000)(2016年7月5日收到;2016年10月10日收到修改稿)

非球形效应对强声场中次Bjerknes力的影响∗

马艳1)2) 林书玉1)† 徐洁1) 唐一璠1)

1)(陕西师范大学陕西省超声学重点实验室,西安 710062)2)(宁夏师范学院物理与电子信息工程学院,纳米结构及功能材料工程技术研究中心,固原 756000)(2016年7月5日收到;2016年10月10日收到修改稿)

考虑了非球形气泡在声场中的形状振动,推导了非球形气泡和球形气泡之间的次Bjerknes力方程,数值模拟了声场中非球形气泡和球形气泡之间的次Bjerknes力和两个球形气泡之间的次Bjerknes力,并对非球形气泡和球形气泡之间的次Bjerknes力的影响因素进行了分析讨论.研究结果表明:当驱动声压振幅大于非球形气泡的Black阈值且又能使得非球形气泡稳定振动时,在第一个声驱动周期内,非球形气泡和球形气泡之间的次Bjerknes力和两个球形气泡的次Bjerknes力方向差异较大,在大小上是两个球形气泡次Bjerkens力的数倍,且有着更长的作用距离.非球形气泡和球形气泡之间的次Bjerknes力取决于非球形气泡的形状模态、两个气泡初始半径的比值、驱动声压振幅、气泡间距和两个气泡的相对位置.

非球形气泡,次Bjerknes力,形状模态

1引 言

声场中气泡之间的相互作用是一个著名的声学现象,会对高压强场中气泡的聚合产生重要影响,例如流光的形成和多泡声致发光(MBSL)等[1−5],在含气泡液体中,气泡受到声场的作用力主要涉及Bjerknes力.Bjerknes力的典型类型有两种:一种是单个气泡在声场中声压波腹处受到的吸引力或排斥力,称为主Bjerknes力,是声场中气泡所受到的主要声场力;第二种是由于驱动声场对气泡作用引起气泡振动,而使得相邻气泡之间产生的相互吸引或排斥力,称为次Bjerknes力或气泡之间的相互作用力.自从Bjerknes力被发现之后,许多作者已经对其进行了实验和理论研究[6−14].Arston等用视频记录了超声驻波引起的气泡的聚集,Crum[10]给出了两个球形气泡之间的次Bjerknes力的简单模型,提出了两个球形气泡之间的次Bjerknes力的方向仅取决于两个球形气泡是否在相位内振动,如果驱动频率位于两个气泡的共振频率之间,两个气泡互相排斥,反之则吸引的经典理论.在一段时间内经典次Bjerknes力理论曾是人们解释气泡之间相互作用的主要理论,但近年来发现,气泡之间的作用力是一个复杂的动力学现象.Yoshida和Takaak[11]用高速摄影机连接长焦距的显微镜观测了两个气泡在次Bjerknes力作用下的运动,特别是次Bjerknes力方向的反转,并与Crum经典次Bjerknes力理论做了比较,发现实验现象并不能用经典的次Bjerknes力理论解释.

随后,多位学者对经典次Bjerknes力理论做了修正,使得气泡之间的次Bjerknes力更接近液体中气泡的真实情况.例如:Zabolotskaya[12]和Ida[13]通过线性模型和两个球形气泡的耦合振动理论证明次Bjerknes力的方向取决于气泡之间的距离.尽管如此,实际声场中,气泡的振动和气泡之间的作用力是非常复杂的声学现象,有很多影响因素,而上述理论中都采用的是线性理论和球形气泡模型.随后Mettin等[14]利用考虑了液体可压缩性的非线性Keller-Miksis模型方程研究了强声场中球对称小振荡空化泡(R＜10µm)间的作用力,结果表明声场强度和方向都会引起次Bjerknes力的变化,他们的研究结果在一定程度上解释了一些经典次Bjerknes力理论所不能解释的实验现象,是次Bjerknes力研究中的一项重要成果.但是Mettin等的研究仍然建立在球形气泡的基础上,而声致发光实验表明:气泡在振荡时,已经不再是标准的球形[15−20],而当两个气泡之间的距离较近时,气泡已经不能完全近似为球形气泡,非球形效应对次Bjerknes力的影响将变得重要[14].强声场中(Pdr＞1.0×105Pa),较近气泡间距时气泡的形变对气泡之间的次Bjerkens力产生什么样的影响,以及次Bjerkens力如何影响气泡的振动和运动,是文本研究的重点内容.由于两个非球形气泡之间的次Bjerknes力非常复杂,两个非球形气泡的形状模态的耦合与否均会对次Bjerknes力产生影响,因此本文只研究了一种特殊情况:一个气泡为非球形气泡,另一个气泡近似为球形气泡,以此来修正球形气泡之间的次Bjerknes力理论,并研究强声场中(Pdr＞1.0×105Pa)较近气泡间距下,非球形效应对次Bjerknes力的影响以及试图用研究结果来解释强声场中泡群的聚合现象例如“streamer formation”和MBSL等现象.

2非球形气泡和球形气泡的次Bjerknes力

对于声场中两个球形气泡,由于气泡在声场中做周期性振动,而使得相邻气泡之间产生相互作用力,两个球形气泡之间的次Bjerknes力可表示为如下形式[14]:

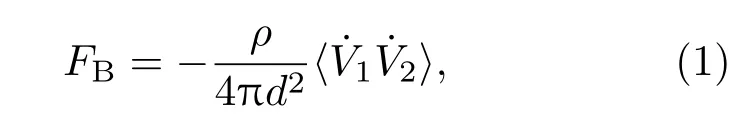
(1)式中FB为两个球形气泡之间的次Bjerknes力,为液体密度;d为两个气泡之间的距离;为两个球形气泡的体积对时间的一阶微分;〈〉表示在一个驱动周期内取平均值,令cB=则两个球形气泡之间的次Bjerknes力的方向取决于〈cB〉的正负,其中〈cB〉大于0为吸引力,〈cB〉小于0为排斥力.

当声场中有两个气泡,假设气泡1为非球形气泡,气泡2近似认为是球形气泡(见图1),非球形气泡壁距气泡中心的距离可表示为[20]

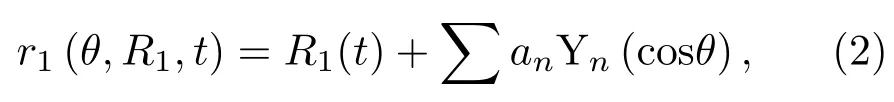
其中R1(t)是非球形气泡1无扰动时的半径,Yn(cosθ)为n阶Legendre函数,an为非球形气泡1的n阶形状模态振幅,且认为非球形气泡为单模态,不存在不同形状模态的耦合.根据Eller类似的推导,非球形气泡1对球形气泡2的作用力为

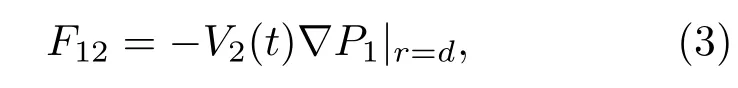
(3)式中V2(t)为气泡2的体积,∇P1为非球形气泡1的声压梯度,根据液体运动方程:

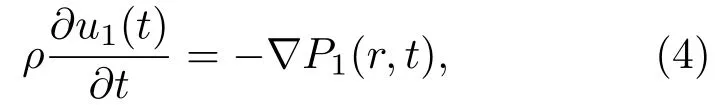
u1(t)为由气泡1振动而引起的液体的振动速度,可表示为

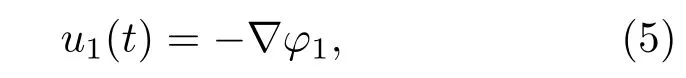
其中φ1为由于非球形气泡1振动而在液体中某一位置处产生的速度势,可表示为[20]

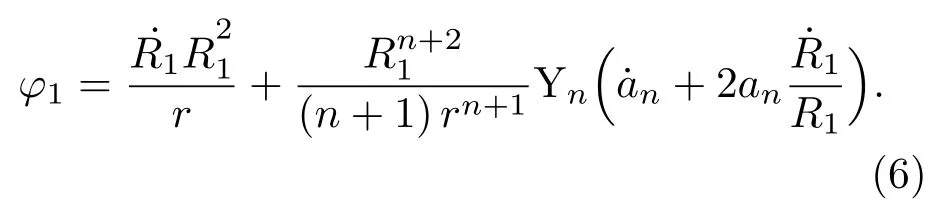
联立(5)和(6)式并对时间微分可得

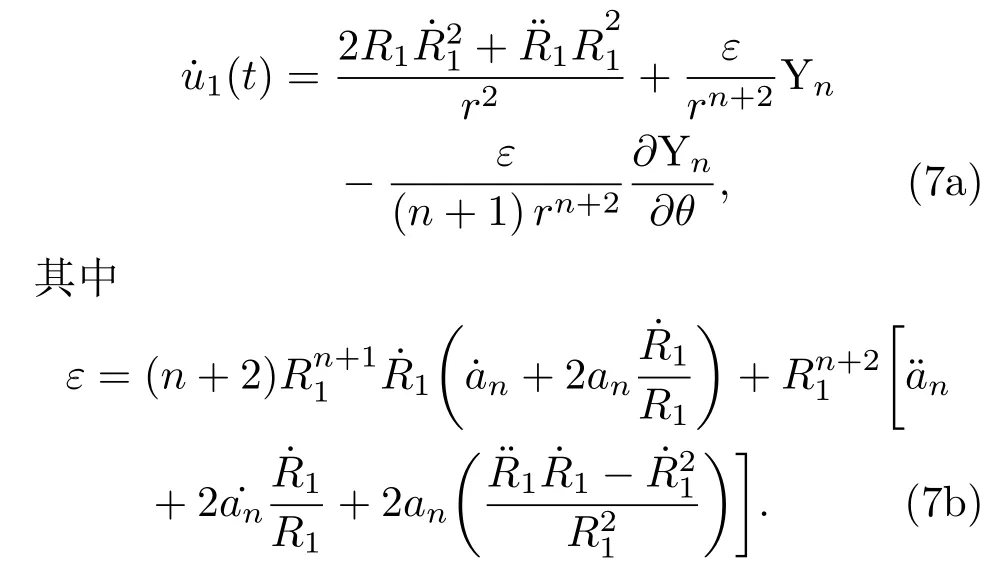
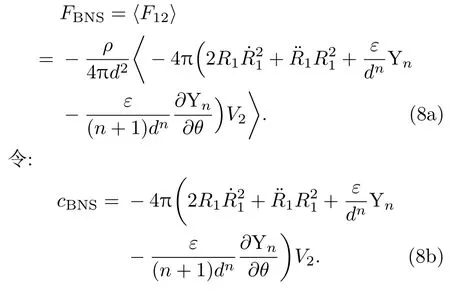
将(4)和(7)式代入(3)式,然后在一个周期内对其取平均可得非球形气泡和球形气泡之间的次Bjerknes力为非球形气泡和球形气泡之间的次Bjerkne力的方向取决于〈cBNS〉的正负,其中,〈cBNS〉大于0为吸引力,〈cBNS〉小于0为排斥力.当气泡2为球形气泡时,an=0,˙an=0,¨an=0.(8)式经微分变形,便回到两个球形气泡之间的次Bjerkne力公式,即(1)式.

图1 声场中的非球形气泡和球形气泡Fig.1.A nonspherical bubble and a spherical bubble in an acoustic fi eld.

当气泡1和2在声场中振动时,气泡振动方程为考虑了气泡之间相互作用的Keller-Miksis方程[9]:

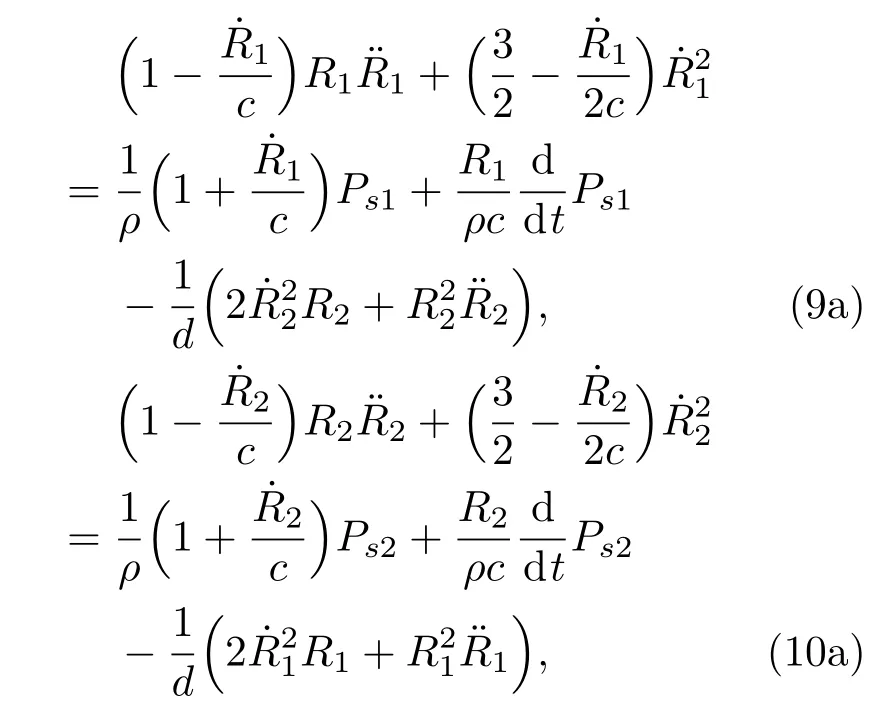
(9a)和(10a)式中R2为气泡2的半径,点代表对时间求导数;c为液体中的声速.其中:

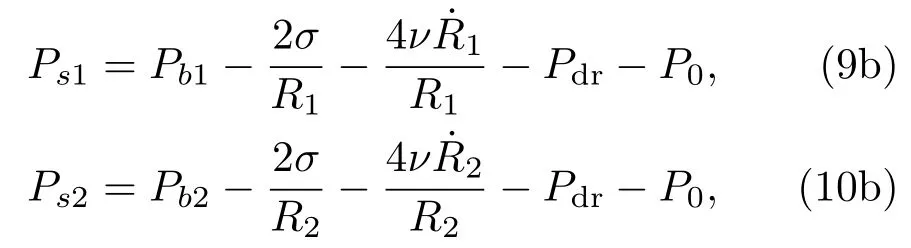
(9b)和(10b)中的Pb1和Pb2分别表示气泡1和2的内部压强,ν为液体的黏滞系数,σ为表面张力系数,非球形气泡1的n阶形状模态振幅an可表示为[21]

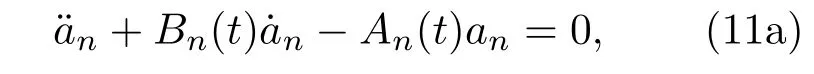
其中:

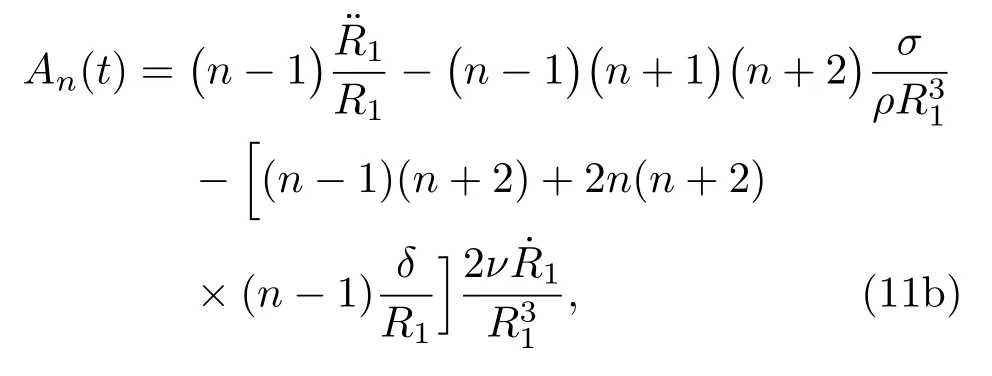
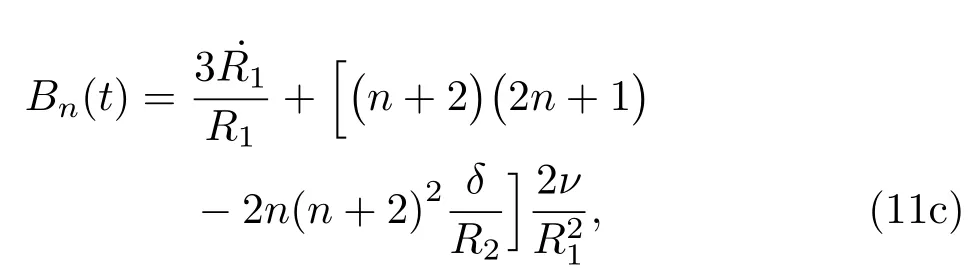
式中δ为气泡1壁周围黏滞引起的涡流层厚度,可表示为

3非球形气泡和球形气泡之间的次Bjerknes力的影响因素

当气泡的初始形状为非球形,在声场的作用下,有两种运动趋势:要么随时间的变化趋于球形,要么随时间变化越来越偏离球形,最终破裂[16−20].对于第二种情况下的次Bjerknes力不属于本文讨论的范围,在这里我们只讨论第一种情况下的次Bjerknes力及其影响因素,即第一个振动周期内非球形气泡的时均次Bjerknes力及其影响因素.经过1个周期或者几个周期后,非球形气泡的形变随时间而趋于零,非球形气泡和球形气泡之间的相互作用力将回到两个球形气泡之间的相互作用力.为了研究这种由非球形效应引起的次Bjerknes力的变化,我们对球形气泡和非球形气泡的次Bjerknes力进行数值模拟,并试图从模拟结果来探讨非球形效应对次Bjerknes力的影响机理.

在以下的数值模拟中,模拟条件为:驱动频率f=20kHz,液体静压强P0=1.01×105Pa,表面张力系数σ=7.25×10−2N/m,水中的声速为:c=1490m/s,驱动声压振幅为Pdr=1.34×105Pa.

图2是两个气泡相对位置不同时,非球形气泡1(2µm)和球形气泡2(4µm)在气泡间距为200µm时,两个气泡之间次Bjerknes力的变化关系曲线.数值模拟结果表明:对于非球形气泡和球形气泡之间的次Bjerknes力而言,其大小与两个气泡的相对位置有关.在上述的模拟条件下,当非球形气泡的长轴和两个气泡中心连线的角度不同,两个气泡之间的次Bjerknes力也不相同,但是相差不大,不同位置处的最大次Bjeknes力为−0.08041µN,最小次Bjerknes力为−0.07993µN,均为吸引力.同样条件下两个球形气泡间的次Bjerknes力为−0.0296µN,也是吸引力.因此,在上述模拟条件下,气泡的非球形效应使得气泡之间的次Bjerknes力较球形气泡间的次Bjerknes力的大小增加了2.7003—2.7166倍.以下的讨论中,我们只讨论非球形气泡长轴平行两个气泡中心连线的情况.

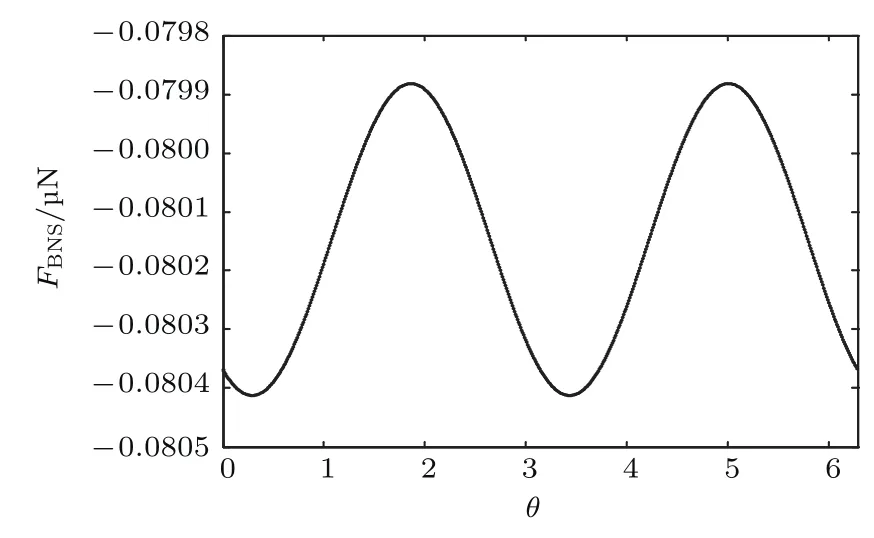
图2 非球形气泡和球形气泡之间次Bjerknes力随两个气泡相对位置变化关系曲线(R10=2µm,R20=4µm,d=200µm)Fig.2.The secondary Bjerknes force between a nonspherical bubble and a spherical bubble vs relative position of two bubbles(R10=2 µm,R20=4 µm and d=200µm).

3.1 非球形气泡形状模态对次Bjerknes力的影响

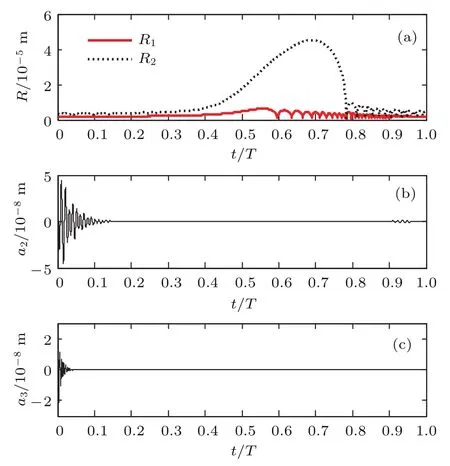
图3 气泡的径向振动和气泡1的2,3阶形状模态振幅随时间的变化(a)气泡1,2的径向振动随时间的变化;(b)气泡1的2阶形状模态随时间的变化;(c)气泡1的3阶形状模态随时间的变化Fig.3.Radial oscillations of two bubbles and the amplitudes of di ff erent shape modes of the fi rst bubblevs time during onedrivingperiod:(a)The radial oscillations of two bubbles;(b)the amplitude of the second-order shape mode of the fi rst bubble;(c)the amplitude of the third-order shape mode of the fi rst bubble.

当非球形气泡的初始半径为2µm,球形气泡的初始半径为4µm,气泡间距为100µm时非球形气泡的2和3阶形状模态振幅如图3(b)和图3(c)所示,可以看出,在驱动声压振幅为1.34×105Pa,驱动频率为20kHz的驱动声场下,非球形气泡的2和3阶形状模态振幅只在第一个振动周期内随时间变化,当非球形气泡的振动时间超过一个周期后,其2和3阶形状模态振幅趋于零,其振动恢复到球形气泡的振动状态.

图4(a)是上述驱动声场下,相距100µm的两个球形气泡在一个驱动周期内的cB随时间的变化关系,图4(b)是同样驱动条件下相距100µm的非球形气泡和球形气泡一个驱动周期内的cBNS随时间的变化关系(n=2),cB和cBNS反映了两个气泡之间的次Bjerknes力的方向和大小在一个周期内随时间的变化关系.对比图4(a)和图4(b)可以看出:在一个驱动周期内,两个球形气泡之间的相互作用力随时间的变化关系与同样条件下非球形气泡和球形气泡之间相互作用力随时间的变化关系差别较大.通过计算可以得到:两个球形气泡之间的〈cB〉=−9.1498×10−20m6/s2,为排斥力;而非球形气泡对球形气泡的〈cBNS〉=1.2940×10−19m6/s2,为吸引力.也就是说在上述的驱动条件和气泡间距下,非球形气泡和球形气泡之间的次Bjerknes力的大小是同样条件两个球形气泡之间的次Bjerknes力的1.414倍,且方向发生改变.

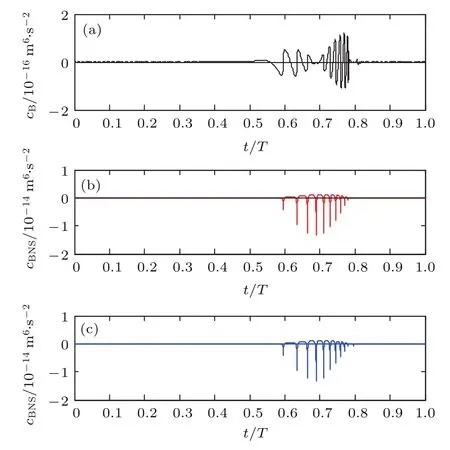
图4 两个气泡之间cB随时间的变化 (a)球形气泡之间cB随时间的变化;(b)非球形气泡和球形气泡之间的cBNS随时间的变化(n=2);(c)非球形气泡和球形气泡之间的cBNS随时间的变化(n=3)Fig.4.The curve of cBbetween two bubbles vs time during one driving period:(a)cBbetween two spherical bubbles;(b)cBNSbetween a nonspherical bubble and a spherical bubble(n=2);(c)cBNSbetween a nonspherical bubble and a spherical bubble(n=3).

同样的驱动声场下,当非球形气泡的形状模态阶数为n=3时,数值模拟结果表明(图4(c)):非球形气泡和球形气泡的〈cBNS〉=3.2678×10−19m6/s2,为吸引力.非球形气泡和球形气泡之间的次Bjerknes力的大小是同样驱动声场中两个球形气泡之间的次Bjerknes力的3.571倍,且方向发生改变.

综上所述:气泡的非球形效应会对气泡的次Bjerknes力产生较大影响,能够在一定的条件下使得球形气泡间的次Bjerknes力改变方向,并且增大数倍.具体原因可能是:非球形气泡在声场中振动,除了径向振动外还有形状振动,对于我们的研究情况而言,虽然形状振动时间非常短,往往在一个或者几个周期内迅速衰减为零,但这种径向振动和形状振动的耦合及形变结束时形变能量转移为振动能量的结果使得一个周期内非球形气泡的辐射声场迅速增加,使之不同于球形气泡径向振动所形成的辐射声场,这种变化使得非球形气泡和球形气泡之间的次Bjerknes力迅速增大,在一定条件下气泡的非球形效应也可能使得气泡之间的次Bjerknes力方向发生改变.而且在上述研究条件下非球形气泡形状模态阶数越大,其形状振动与径向振动耦合产生的辐射声压梯度越大,对周围气泡产生更强的作用力.

由此可以看出,当声场中的驱动声压振幅大于气泡的Black空化阈值,非球形气泡长轴与气泡间距平行时,在较近的气泡间距下,非球形气泡和球形气泡之间的次Bjerknes力和同样初始尺寸的两个球形气泡之间的次Bjerknes力的差异较大,与Mettin理论中预测的强声场中(＞1×105Pa)两个球形气泡之间次Bjerknes力的变化有一定差异,而这些差异也可能是强声场中形成的“stream formation”和MBSL的原因.

3.2 气泡间距对球形气泡和非球形气泡的次Bjerknes力的影响

两个气泡之间的距离是影响气泡次Bjerknes力的重要因素,两个球形气泡的次Bjerknes力会随着气泡间距的增大而逐渐减小,当两个气泡之间的距离大于一定值时,两个球形气泡就会成为两个无耦合的自由气泡,此时两个球形气泡之间的次Bjerknes力可忽略不计.为了研究非球形效应对气泡之间的次Bjerknes力的影响因素,我们研究了不同气泡间距下非球形气泡和球形气泡之间的次Bjerknes力,并与同样条件下的两个球形气泡之间的次Bjerknes力做了对比.在以下的讨论中,我们只考虑非球形气泡做2阶形状模态振动的情形.

图5是不同气泡间距下的两个气泡的次Bjerknes力的对数随气泡1的初始半径变化曲线,图5(a)—(d)中黑色虚线代表非球形气泡和球形气泡的次Bjerknes力对数的变化,红色实线代表了同样条件下的两个球形气泡的次Bjerknes力对数的变化,对比可以发现,当非球形气泡的初始半径保持不变(R20=2µm),球形气泡2的初始半径从0.5µm变化到10µm的过程中,当两个气泡的初始半径为一定比例时,非球形气泡和球形气泡之间的次Bjerknes力是同样条件下两个球形气泡之间的次Bjerknes力的几倍到十几倍.而除此之外,非球形气泡和球形气泡之间的次Bjerknes力近似等于同样条件下的两个球形气泡之间的次Bjerknes力.当两个气泡之间的距离增大到500µm和1000µm时,通过数值模拟可以看出,两个球形气泡之间的次Bjerknes力非常小,趋于0,而同样尺寸的非球形气泡和球形气泡之间的次Bjerknes力也随着气泡间距的增加出现了衰减,但相较同样条件下的两个球形气泡之间的次Bjerknes力,仍然保持一个较大的数量级,如图5(c)—(d).这说明:非球形气泡和球形气泡之间的次Bjerknes力有更大的作用距离,能够使得相邻的气泡在较远的距离处仍然受到相当大小的次Bjerknes力作用,该结果与文献[11]中的实验结果相一致.

数值模拟结果表明:非球形气泡和球形气泡之间的次Bjerknes力,随气泡间距的变化关系不同于同样尺寸下两个球形气泡之间的次Bjerknes力随气泡间距的变化关系,这是由于非球形气泡的形状振动,使得不同的气泡间距下,不同初始半径的球形气泡和非球形气泡对的耦合模式完全不同,虽然会出现次Bjerkens力随气泡间距减小的整体趋势,但仍然会出现一些特殊比例的气泡对的次Bjerknes力在小气泡间距下较小或者在大气泡间距下较大(图5(a)—(d)).除此之外,数值模拟结果表明非球形气泡和球形气泡之间的次Bjerknes力的作用距离更长,当气泡距离大于1000µm以上才逐渐衰减为0.

图5 (网刊彩色)不同气泡间距下两个气泡之间的次Bjerknes力的对数随气泡2初始半径的变化曲线(Pdr=1.34×105Pa,R10=2µm) (a)d=100µm;(b)d=200µm;(c)d=500µm;(d)d=1000µmFig.5.(color online)The curve of the logarithm of the secondary Bjerknes force between two bubbles vs the radius of the second bubble(Pdr=1.34×105Pa,R10=2µm):(a)d=100µm;(b)d=200µm;(c)d=500µm;(d)d=1000µm.

3.3 驱动声压振幅对球形气泡和非球形气泡之间的次Bjerknes力的影响

图6是不同驱动声压振幅下的非球形气泡和球形气泡之间的次Bjerknes力的对比图,其中图6(a)是两个气泡之间距离为200µm时,两个球形气泡的次Bjerknes力随驱动压强振幅的变化关系.图6(b)是两个气泡之间距离为200µm时,非球形气泡和球形气泡之间的次Bjerknes力随驱动压强的变化关系,对比数据可以发现,两个球形气泡之间的次Bjerknes力和非球形气泡和球形气泡之间的次Bjerknes力的大小都随着驱动声压振幅的增加而增加.当驱动声压振幅为1.30×105Pa和1.32×105Pa时,两个球形气泡之间的次Bjerknes力和同样气泡间距、同样初始尺寸的非球形和球形气泡之间的次Bjerknes力的大小相差不多.当驱动声压振幅增大到1.34×105Pa时,数值模拟结果表明,非球形气泡和球形气泡之间的次Bjerknes力是同样条件下两个球形气泡之间的次Bjerknes力的几倍甚至十几倍以上.

综上所述：当驱动声压振幅使得非球形气泡能够稳定振动而不破裂时,驱动声压振幅越大,非球形效应对次Bjerknes力的影响越大,特别是当驱动声压振幅超过两个气泡的Black阈值后,使得非球形气泡和球形气泡之间的次Bjerknes力的大小迅速增大,远大于两个球形气泡之间的Bjerknes力.非球形效应随声压振幅增加的原因是,驱动声压越强,非球形气泡的径向振动幅度和形状振动幅度也越大,特别是当驱动声压振幅增加到非球形气泡的空化阈值之上,其在一个驱动周期内径向振动和形状振动耦合形成的平均辐射声场梯度将大幅度增加,此时,非球形气泡和球形气泡之间的次Bjerknes力也迅速增大.因此,驱动声压振幅越大,非球形效应对次Bjerknes力的影响越显著.

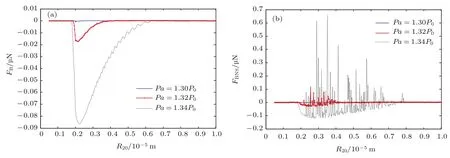
图6 (网刊彩色)不同驱动声压振幅下两个气泡之间的次Bjerknes力随气泡2初始半径的变化(R10=2µm,d=200µm)(a)两个球形气泡之间的次Bjerknes力;(b)非球形气泡和球形气泡的次Bjerknes力Fig.6.(color online)The curve of the secondary Bjerknes force between two bubblesvsthe radius of the second bubble(R10=2 µm,d=200 µm):(a)The secondary Bjerknes force between two spherical bubblest;(b)the secondary Bjerknes force between anonspherical bubble and a pherical bubble.

4结 论

本文在Crum和Mettin等关于球形气泡的次Bjerknes力的研究基础上,考虑了声场中非球形气泡的形状振动对次Bjerknes力的影响,推导了非球形气泡和球形气泡之间的次Bjerknes力方程,数值模拟了非球形气泡和球形气泡之间的次Bjerknes力并与两个球形气泡之间的次Bjerknes力进行了对比.

研究发现:当声场驱动声压大于非球形气泡的Black阈值时且使得非球形气泡能够稳定振动时,非球形气泡和球形气泡之间的次Bjerknes力在大小和方向上都不同于两个球形气泡之间的次Bjerknes力,作用力在数量级上大于同样条件下的两个球形气泡之间的次Bjerknes力;非球形效应对次Bjerknes力的影响取决于非球形气泡的形状模态、两个气泡初始半径的比值、驱动声压振幅、气泡间距和两个气泡的相对位置.

在以往的研究中,线性条件下两个球形气泡之间的次Bjerknes力非常小,人们往往忽略其影响,对于气泡聚合等实验现象不能给出合理的解释.我们的研究发现,在非线性条件下,单个气泡的非球形效应使得次Bjerknes力较Mettin非线性理论中球形气泡间的次Bjerknes力在方向和数量级上有一定的差异,能够使一定尺寸的气泡对的次Bjerknes力增加几倍到十几倍.研究结果虽然只反映了第一个驱动周期次Bjerknes力的变化,但由于在第一个振动周期内非球形效应的影响,已经使得气泡的运动状态发生了较大变化,进而影响了气泡随后的运动.非球形效应使得两个气泡之间具有相当大小的作用力,使得气泡聚合或者分离现象能够发生,产生一些稳定的气泡结构,也能够改变快速运动的小气泡的运动趋势,这可能也是“stream formation”的主要原因;对于强声场中的气泡群,较大的次Bjerknes力能够使气泡的空化效应更容易发生,这可能也是实验中多泡声致发光更易发生的一个重要原因.两个气泡都发生形变及气泡形变耦合对次Bjerknes力的影响将是我们下一步的工作.

[1]Anthony H,Kaper T 2001 J.Fluid Mech.445 377

[2]Thomas J M,Sean M C 1997 J.Acoust.Soc.Am.102 1522

[3]Rossello J M,Dellavale D,Bonetto F J 2015 Ultrason.Sonochem.22 59

[4]Yuan L,Joseph K 2013 Phys.Fluids 25 073301

[5]Eller A 1968 J.Acoust.Soc.Am.43 107

[6]Alexander A D 1997 J.Acoust.Soc.Am 102 747

[7]David R,Pierre T B 2011 Phys.Fluids 23 042003

[8]Mohammad A A 2011 J.Acoust.Soc.Am.130 3321

[9]Rasoul S B,Nastaran R 2010 Phys.Rev.E 82 016316

[10]Crum L A 1975 J.Acoust.Soc.Am.57 1363

[11]Yoshida K J,Takaaki F 2011 J.Acoust.Soc.Am 130 135

[12]Zabolotskaya E A 1984 Sov.Phys.Scoust 30 365

[13]Ida M 2007 Phys.Rev.E 76 04309

[14]Mettin R,Akhatov I,Parlitz U 1997 Phys.Rev.E 56 2924

[15]Shao W H,Chen W Z 2013 J.Acoust.Soc.Am.133 119

[16]Prosperetti A 1977 Q.Appl.Math 34 339

[17]Bogoyavlenskiy V A 2000 Phy.Rev.E 62 2158

[18]Pelekasis N A,Tsamopouslos J A 1990 Phys.Fluids A 2 1328

[19]Xie C G,An Y 2003 Acta Phys.Sin.52 102(in Chinese)[谢崇国,安宇2003物理学报52 102]

[20]Plesset M S 1954 J.Appl.Phys.25 96

[21]Brenner M P,Lohse D,Dupon T F 1995 Phys.Rev.Lett.75 954

PACS:43.25.+y,43.35.+d,47.55.ddDOI:10.7498/aps.66.014302

*Project supported by the National Natural Science Foundation of China(Grant Nos.11374200,11674206).

†Corresponding author.E-mail:sylin@snnu.edu.cn

In fl unece of nonspherical e ff ects on the secondary Bjerknes force in a strong acoustic fi eld∗

Ma Yan1)2)Lin Shu-Yu1)†Xu Jie1)Tang Yi-Fan1)

1)(Shaanxi Key Laboratory of Ultrasonics,Shaanxi Normal University,Xi’an 710062,China)2)(College of Physics and Electronic Information Engineering,Engineering Research Center of Nanostructure and Functional Materials,Ningxia Normal University,Guyuan 756000,China)(Received 5 July 2016;revised manuscript received 10 October 2016)

The secondary Bjerknes force between bubbles in an acoustic fi eld is a well-known acoustic phenomenon.The theoretical researches of the secondary Bjerknes force mainly focus on the case of two spherical bubbles.The secondary Bjerknes force between two spherical bubbles,calculated based on the linear equations,is very small and negligible.Therefore these theoretical researches donot give a good explanation for the phenomenon,such as“streamer formation”and multi-bubble sonoluminescence(MBSL).Experiments of sonoluminescence show that the shapes of the bubbles in a sound fi eld are not entirely spherical.Nonspherical e ff ects have an important in fl uence on the secondary Bjerknes force when two bubbles come close to each other in a strong acoustic fi eld(＞ 1.0× 105Pa).How the shape distortion of a nonspherical bubble causes the secondary Bjerknes force between two bubbles to change,and how the secondary Bjerknes force a ff ects the oscillations and movements of bubbles are major problems which we are to solve in the present research.The expression of the secondary Bjerknes force between a nonspherical bubble and a spherical bubble is obtained by considering the shape oscillation of a nonspherical bubble.We numerical simulate the secondary Bjerknes force between a nonspherical bubble and a spherical bubble based on the nonlinear oscillation equations of two bubbles,and compare the secondary Bjerknes force between a nonspherical bubble and a spherical bubble with the secondary Bjerknes force between two spherical bubbles in the same condition.We discuss the in fl uence of nonspherical e ff ects on the secondary Bjerknes force between two bubbles.The results show that when the amplitude of driving pressure is greater than the Blake threshold of a nonspherical bubble and makes the bubble oscillate stably,the secondary Bjerknes force between this nonspherical bubble and a spherical bubble is di ff erent from the secondary Bjerknes force between two spherical bubbles in direction and magnitude.The secondary Bjerknes force between a nonspherical bubble and a spherical bubble is much bigger than that between two spherical bubbles.The interactional distance of the secondary Bjerknes force between a nonspherical bubble and a spherical bubble is longer than that between two spherical bubbles.The secondary Bjerknes force between a spherical bubble and a nonspherical bubble depends on the radii of two bubbles,distance between two bubbles,shape mode of the nonspherical bubble and the amplitude of driving pressure.Our research is closer to the actual bubbles in liquid.We also prove that big mutual interaction between bubbles is the main cause for froming a stable structure between bubbles.For bubbles,big mutual interaction causing the cavitation becomes easier.These results are important for explaining the phenomenon in an acoustic fi eld,such as“streamer formation”and MBSL.

nonspherical bubbles,secondary Bjerknes force,shape mode

10.7498/aps.66.014302

∗国家自然科学基金(批准号:11374200,11674206)资助的课题.

†通信作者.E-mail:sylin@snnu.edu.cn