行星飞轮式滚珠丝杠惯容器设计与特性分析

葛 正 王维锐

(浙江大学机械工程学院，杭州310027)

行星飞轮式滚珠丝杠惯容器设计与特性分析

葛 正 王维锐

(浙江大学机械工程学院，杭州310027)

为提高滚珠丝杠型惯容器的惯容系数与飞轮质量之比(惯-质比)，提出了行星飞轮式滚珠丝杠惯容器设计方案。建立了惯容器力学模型，研究了惯容器各结构参数对飞轮惯-质比的影响规律，通过增加行星轮数量或厚度、减小销轴半径等提高行星轮自转惯量占飞轮总惯量比重的方法，有效提高了惯-质比;根据行星轮数量、厚度和销轴半径，计算得到最优的行星轮与外齿圈齿数比，令惯-质比达到最大。对比了行星飞轮和传统单飞轮惯容器的力学特性，表明在同等飞轮径向尺寸下，行星飞轮可获得更大惯-质比。最后通过试验，验证了理论分析的正确性。

惯容器;行星飞轮;滚珠丝杠;惯-质比

引言

2002年剑桥大学SMITH［1］根据电容的数学模型提出了一种新型的两端点机械装置Inerter，该装置的受力与两端点相对加速度成正比。由于惯容器在机械网络中的动力学特性与电容在电学网络中的特性相同，陈龙等［2］引入这一概念时，将其翻译为惯性蓄能器或惯容器。

惯容器一方面具有质量块所不具备的两端特性(质量块相当于单端接地的惯容器)，另一方面能取代质量块并以较小的自身质量实现大惯性体的动力学特性，因此丰富了机械振动网络的设计理论。如将动力吸振器中的质量块替换为惯容器后，整体质量可降低90%以上，令轻型动力吸振器成为可能。该技术已被应用到车辆悬架、建筑等多个领域［3－7］。惯容器运用在车辆零部件的力学测试系统中，可进一步实现测试台架与被测零部件的机械阻抗匹配，从而提高试验台架综合性能。

当前惯容器的结构形式有滚珠丝杠型［8］、齿轮齿条型［9］、液压马达型［10］、液力发生型［11］、液力回旋型［12］等。其中滚珠丝杠型惯容器的摩擦力较小，能够利用螺母的预紧力减小背隙影响，同等质量惯容系数较大，综合表现较优［13］。由于滚珠丝杠惯容器的独特优势，目前针对安装单个飞轮的滚珠丝杠惯容器的理论研究相对较为深入，并成为多种新型惯容器的结构基础。一些学者研究了滚珠丝杠惯容器的固有特性［14－17］。一些学者则在滚珠丝杠惯容器的基础上增设调节部件，形成可动态调节的新型惯容器［18－20］。

尽管当前对滚珠丝杠式惯容器有了较多研究，但对如何用更小的飞轮质量实现更大惯容系数的研究鲜有见述。尤其当飞轮径向尺寸受限时，单飞轮惯容器无法通过改变其结构参数或增设定轴轮系提高其惯-质比放大能力。为进一步提高滚珠丝杠型惯容器的飞轮惯-质比，本文提出一种行星飞轮式滚珠丝杠惯容器，利用行星轮的公转和自转复合运动，增大惯容器的飞轮惯-质比。通过理论分析，建立惯容系数和惯-质比的数学模型，探明结构要素对惯-质比的影响规律。最后通过试验验证理论分析的正确性。

1 惯容器结构设计及惯容系数的理论分析

1.1 惯容器结构设计

如图1所示，行星飞轮式滚珠丝杠惯容器的活塞杆和外壳分别为惯容器的2个运动端。活塞杆左端加工有螺纹，外壳上设置有安装法兰，用于同其他部件连接。当惯容器2个运动端之间发生相对运动时，活塞杆沿着直线轴承和直线导轨方向推动螺母左右移动，螺母继而将直线运动转换为丝杠的旋转运动。飞轮由行星飞轮架和多个行星飞轮共同组成，行星飞轮架与丝杠一端固定，行星轮则通过外齿与外齿圈的内齿相啮合。运动中，丝杠与行星飞轮架等速旋转，行星飞轮则在飞轮架以及外齿圈的共同作用下，形成既有公转又有自转的复合运动。

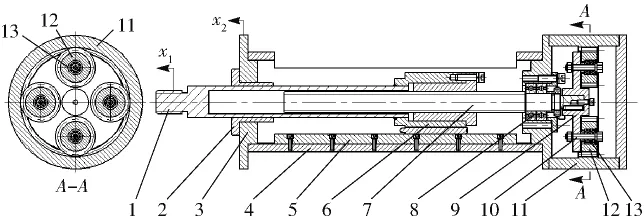
图1 行星飞轮式滚珠丝杠惯容器结构Fig．1 Structure of ball screw type inerter with planetary flywheel

1.2 惯容器的惯容系数解析

当齿轮模数相对于飞轮组径向尺度较小时，为便于分析，假设行星轮、飞轮架及其上的轴销都是均质圆柱体，外齿圈内半径和飞轮架外半径近似等于外齿圈分度圆半径，行星轮半径近似等于自身分度圆半径。惯容器的原理简图如图2所示(隐去了外壳仅保留行星飞轮、丝杠螺母和活塞杆部分)。

图2 行星飞轮式滚珠丝杠惯容器原理图Fig．2 Schematic diagram of planetary flywheel inerter

图2中，x1、x2为两端位移，R为外齿圈分度圆半径，r为行星轮分度圆半径，s为飞轮架轴销半径，l为行星轮厚度，L为飞轮架厚度，H为飞轮总厚度。

根据能量守恒定律得

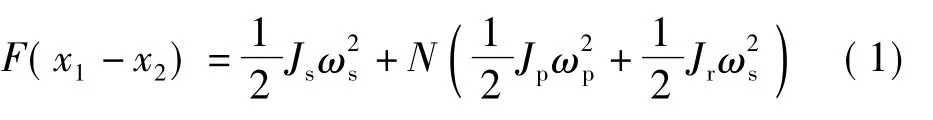
式中 F——惯容器输出力

N——行星轮数量

Js——飞轮架转动惯量(含轴销)

Jp——行星轮自转转动惯量

Jr——行星轮公转转动惯量

ωs——飞轮架-螺母相对角速度

ωp——行星轮自转角速度

两侧同取微分得

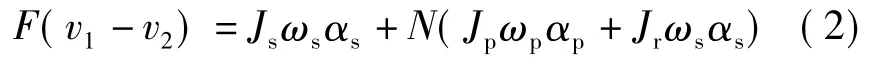
式中 v1、v2——两端速度

αs——飞轮架-螺母相对角加速度

αp——行星轮自转角加速度

根据行星轮系的转动关系有

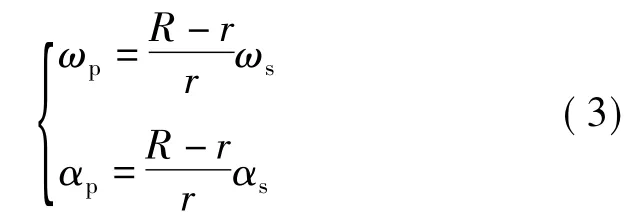
将式(3)代入式(2)得

根据丝杠传动关系有

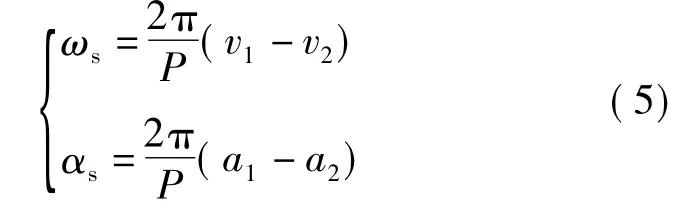
式中 P——丝杠导程

a1、a2——两端加速度将式(5)代入式(4)得

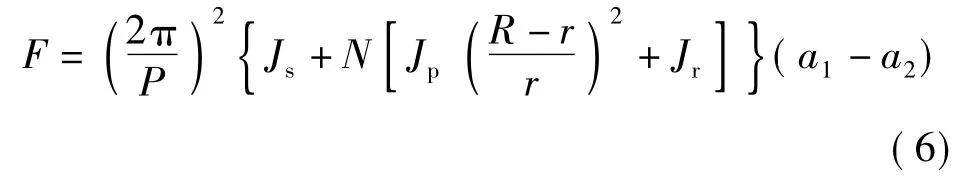
设飞轮架、行星轮密度为ρ，分别计算其质量和转动惯量为

将式(8)代入式(6)得

因此行星飞轮式滚珠丝杠惯容器的输出力与两端相对加速度成正比，符合惯容器力学特性定义。其惯容系数为

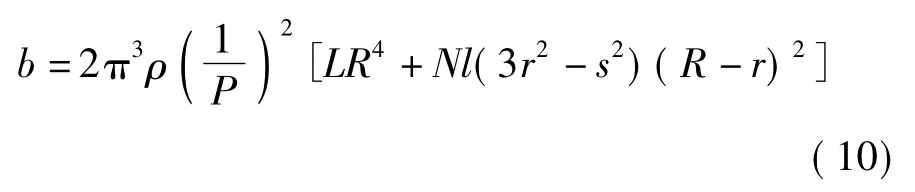
由材料密度、丝杠导程、外齿圈分度圆半径、行星轮分度圆半径和厚度、飞轮架厚度和销轴半径、行星轮数量确定。

对式(10)做归一化处理，得到惯容系数计算模型

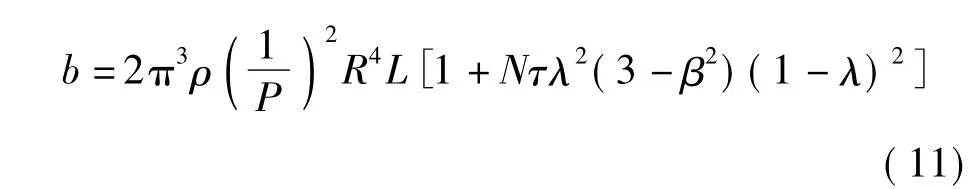
其中

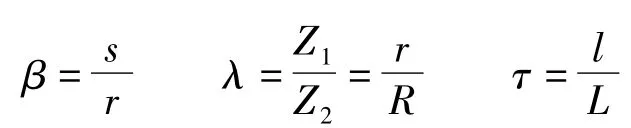
式中 Z1——行星轮齿数 Z2——外齿圈齿数

β——销轴与行星轮分度圆半径比

λ——行星轮与外齿圈齿数比

τ——行星轮与飞轮架厚度比

2 惯容器最优结构参数解析

机械网络设计时，需根据使用要求，确定惯容器的惯容系数。由于惯容器能用小质量的飞轮实现大质量物体的动力学特性，因此惯容系数与飞轮质量比越大，则减质量效果愈加明显。行星飞轮式滚珠丝杠惯容器的最优结构参数求解问题可以等效为惯容器在目标惯容系数约束下，求解结构参数令惯容器的惯-质比达到最大。

2.1 惯-质比的计算

对行星飞轮滚珠丝杠惯容器来说，其惯-质比为

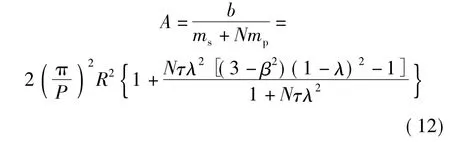
式中 mp——行星轮质量

ms——飞轮架质量(含轴销)

可见，行星飞轮式滚珠丝杠惯容器的惯-质比包括两部分:第一部分受丝杠导程P和外齿圈分度圆半径R影响;第二部分受飞轮数量N、行星轮与飞轮架厚度比τ、行星轮与外齿圈齿数比λ、销轴与行星轮分度圆半径比β影响。

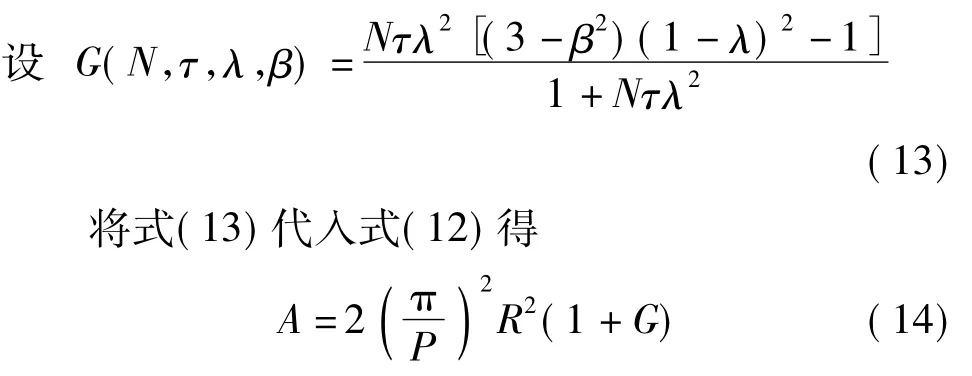
减小丝杠导程能提高惯-质比，但会引起丝杠寿命和传动效率降低，所以确定丝杠导程后，提高惯-质比的最有效途径是增大飞轮的径向尺寸，由于飞轮的径向尺寸不可能无限增大。因此优化问题应在特定的丝杠导程和飞轮径向尺寸下进行讨论。

根据式(14)，当丝杆导程和飞轮径向尺寸确定时，惯容器的惯-质比与G正相关，结构参数对G的影响规律等效于结构参数对惯-质比的影响规律，因

此惯容器的参数优化问题可表示为

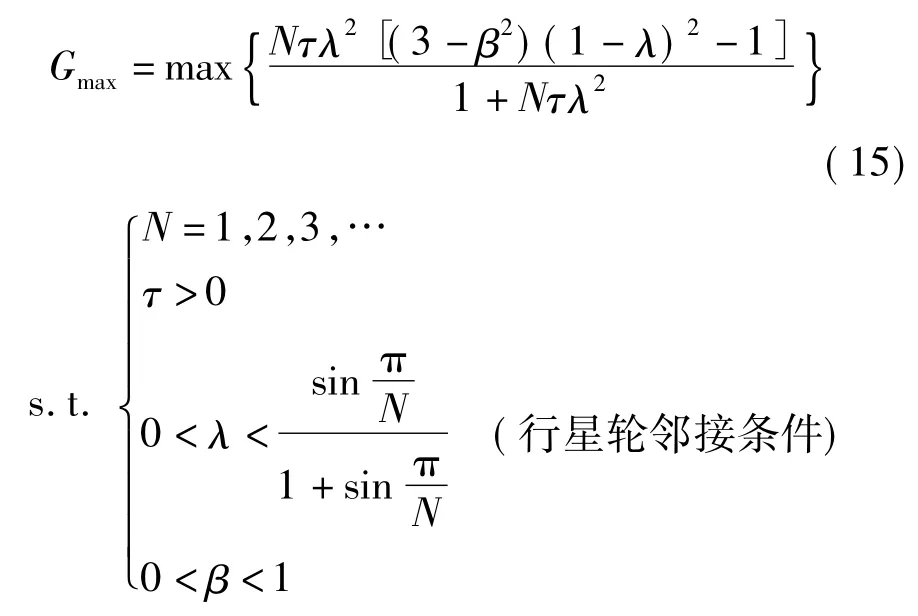
2.2 结构参数对惯-质比的影响规律

将式(13)右侧上下同除以Nτ得

可见惯-质比与行星轮数量N、行星轮与飞轮架厚度比τ正相关;同销轴与行星轮分度圆半径比β负相关。因此增大N、τ或减小β，即增加行星轮自转惯量占飞轮总惯量的比重，有助于提高惯-质比。

λ、N、τ和β与G关系如图3～5所示。

图3 λ、N与G关系(τ=2，β=0.2)Fig．3 Relationship betweenλ，N and G(τ=2，β=0.2)

图4 λ、τ与G关系(N=4，β=0.2)Fig．4 Relationship betweenλ，τand G(N=4，β=0.2)

图5 λ、β与G关系(N=4，τ=2)Fig．5 Relationship betweenλ，βand G(N=4，τ=2)

由图3～5可见，当λ∈(0，λmax)时，存在最优λopt令G达到最大。

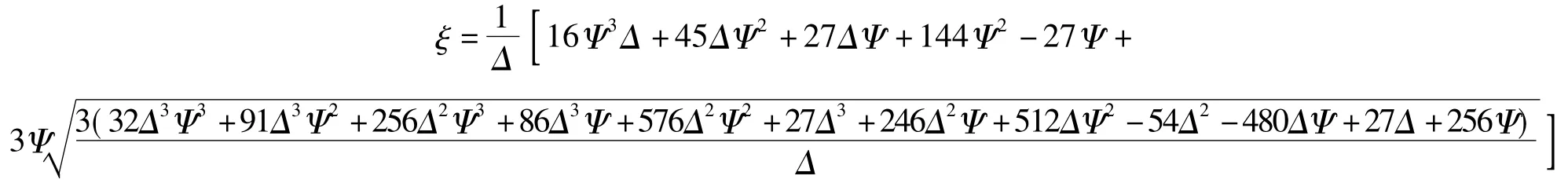
2.3 行星飞轮惯容器的参数设计流程

根据上述分析，行星飞轮惯容器的参数设计流程为:①根据丝杠受力条件，选定导程P。②选定径向空间允许的最大飞轮径向尺寸Rmax。③选择较大的飞轮数N和行星轮与飞轮架厚度比τ、较小的销轴半径比β。④根据式(20)计算最优齿数比λopt。⑤根据式(11)计算飞轮架厚度L。⑥根据目标惯容系数计算确定其他结构参数。

2.4 单飞轮和行星飞轮惯容器对比

对图6所示的单飞轮滚珠丝杠惯容器来说，其惯-质比为

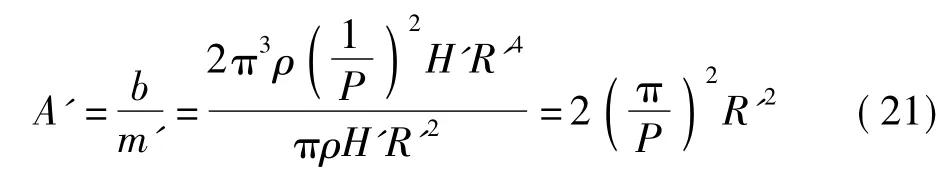
图6 单飞轮滚珠丝杠型惯容器Fig．6 Ball screw type inerter with single flywheel

惯-质比由丝杠导程和飞轮径向尺寸确定，与飞轮厚度无关。较小的丝杠导程或较大的飞轮径向尺寸能获得较大的惯-质比。

2种惯容器实现相同惯容系数时有

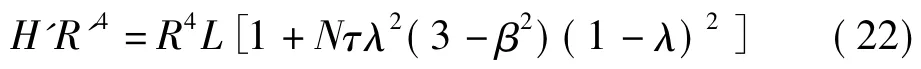
两者飞轮径向尺寸相同时，R=R'。由式(21)可知，当飞轮径向尺寸受限时，单飞轮惯容器的惯-质比被锁定，无法通过结构参数调整。2种惯容器的惯-质比关系为

两者飞轮厚度关系为

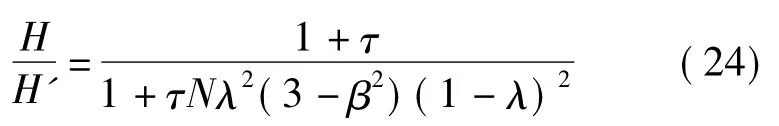
因此，在飞轮径向尺寸约束下，为达到相同的惯容系数，行星飞轮式惯容器的飞轮质量小于单飞轮惯容器，但需要相对较大的飞轮厚度。

3 试验

3.1 样机制作与台架试验

采用图1所示结构方案，设计并制作行星飞轮惯容器。作为参照，同时制作4种采用不同结构参数的行星飞轮，以及与1号行星飞轮径向尺寸和总厚度均相同的单飞轮。主要结构参数如表1所示。

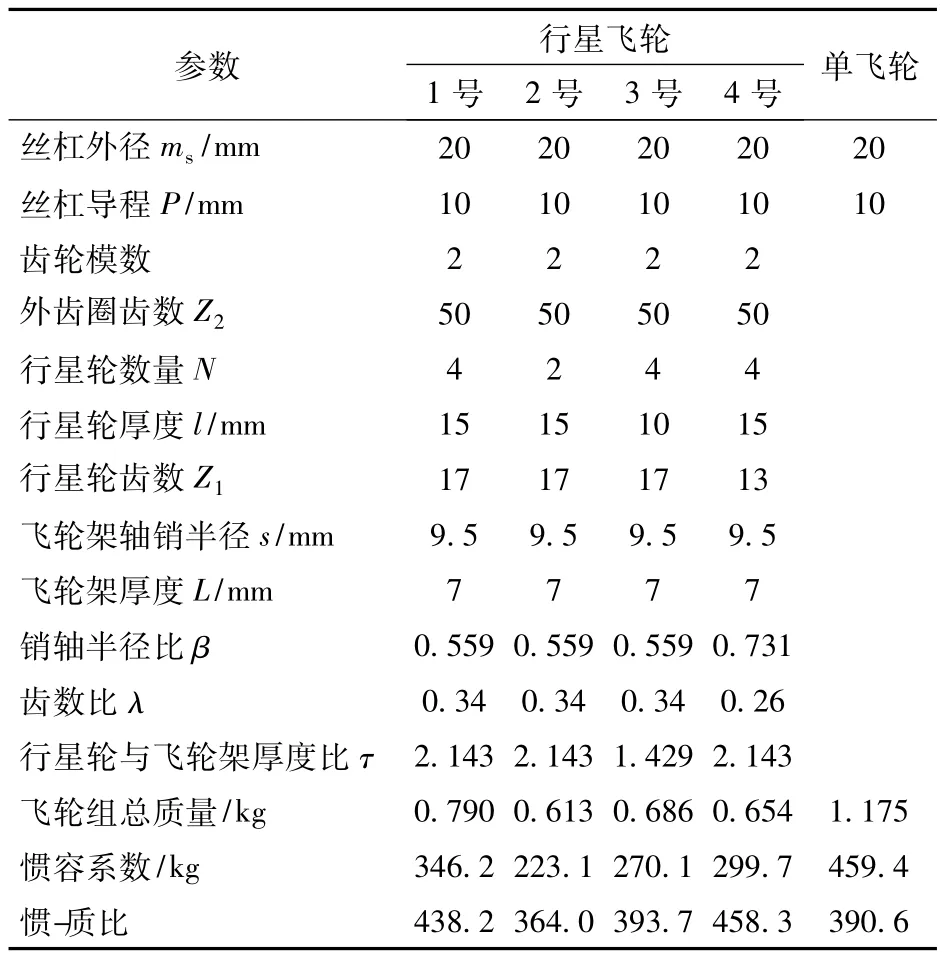
表1 行星飞轮式滚珠丝杠惯容器零件结构参数Tab．1 Structure parameters of parts of ball screw typeinerter w ith planetary flywheel

通过对惯容系数的理论计算，并实测飞轮质量可知:对比2号和1号飞轮，行星轮数量从2增加到4后，飞轮惯-质比提高了20.4%;对比1号和3号飞轮，行星轮与飞轮架厚度比τ下降了66.7%，飞轮惯-质比降低了10.1%;对比1号和4号飞轮，虽然4号飞轮的销轴半径比β更大，但其齿数比(λ= 0.26)更接近最优齿数比(λopt=0.24)，飞轮惯-质比提高了4.6%;对比4号飞轮和单飞轮，在相同的径向尺寸情况下，4行星飞轮的惯-质比相对单飞轮提高了17.3%，表现出显著的减质量优势。

制作2种飞轮以及惯容器样机，如图7、8所示。

图7 行星飞轮与单飞轮样机Fig．7 Prototype of planetary flywheel and single flywheel

搭建试验台架(图9、10)，液压缸固定在试验台承载框架的一端，惯容器通过前端法兰面与试验台承载框架的另一端固定，液压杠的作动杆前端安装力传感器，并通过连接器与惯容器的活塞杆连接。通过MOOG Portable控制器控制液压缸，液压缸驱动惯容器的活塞杆与其壳体产生相对运动。由NICompact-RIO数据采集系统实时采集惯容器活塞杆的位移和力信号并发送给计算机，供后续数据分析。

图8 惯容器样机Fig．8 Prototype of inerter

图9 试验台架原理图Fig．9 Schematic of test bed

图10 惯容器样机及试验台架Fig．10 Prototype of inerter and test bed

3.2 正弦输入试验

通过液压作动缸，令惯容器活塞杆与外壳之间发生幅值为7 mm，频率为5 Hz的正弦运动。记录过程中惯容器两端相对位移和作用力，作用力的时间响应曲线如图11所示。

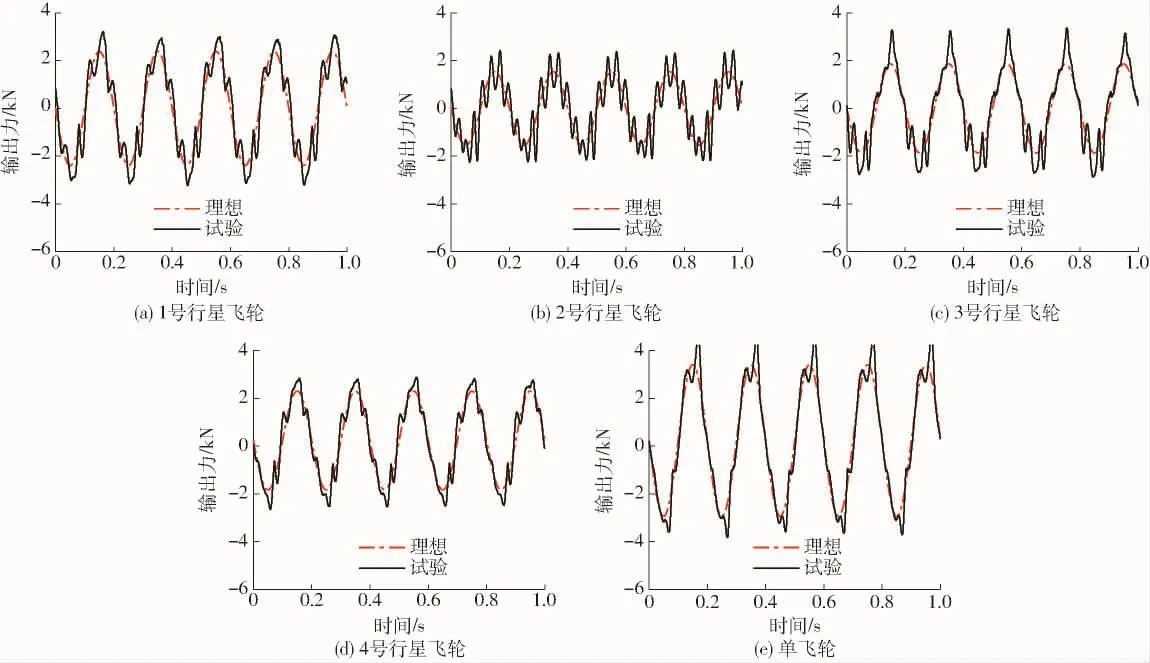
图11 惯容器输出力的时间响应(位移幅值7mm，频率5 Hz)Fig．11 Time responses of output force of inerters

由图11可见，惯容器输出力均基本与理论计算结果相吻合，表明对惯容系数的理论计算是正确的。

3.3 随机输入试验

通过液压作动缸给1号行星飞轮和单飞轮惯容器输入如图12所示，频率范围为0.5～15 Hz的速度白噪声，其功率谱密度函数(m2/Hz)为

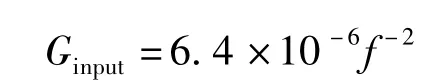
式中 f——频率，Hz

分析试验数据，得到输出力的功率谱密度和位移-输出力传递特性(图13)。由图13可见，行星飞轮和单飞轮惯容器位移-力传递特性相似，表明在该频段行星式飞轮可以替代单飞轮作为滚珠丝杠惯容器的惯性部件。其中低频段，两者的输出特性基本相同，这主要是因为摩擦力的影响较大，惯容特性体现尚不明显［14］;高频段，两者的位移频响均随频率提高而增大，符合理想惯容器的特性规律，增益的差异主要是因为2种惯容器的惯容系数不同。

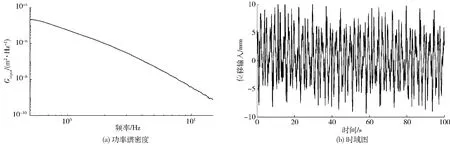
图12 随机输入Fig．12 Radom inputs

图13 惯容器输出力的频率响应Fig．13 Frequency response of output force of inerters

综合图11和图13来看，行星飞轮与单飞轮惯容器的动态特性相似，但由于摩擦、粘滞等非线性因素，导致输出力响应曲线均发生一定程度的畸变，输出与理想惯容器有一定差异，其形成机理应进一步研究。

4 结论

(1)行星飞轮能用作滚珠丝杠惯容器中的惯性部件，并且相对单飞轮来说，能大幅提高滚珠丝杠惯容器的飞轮惯-质比。

(2)行星飞轮惯容器的惯-质比可通过多个结构参数进行调节，增加行星轮数量、加厚行星轮、减小飞轮架销轴半径，即提高行星轮的自转惯量占飞轮总惯量比重，均能提高惯-质比。根据以上3个参数，可计算得到最优的行星轮与外齿圈齿数比，令惯-质比达到最大。

(3)相同径向尺寸限制下，达到相同的惯容系数，行星飞轮组厚度大于单个飞轮。因此行星飞轮惯容器适用于对惯容器自重敏感而轴向空间相对充裕的场合。

1 SMITH M．Synthesis ofmechanical networks:the inerter［J］．IEEE Transactions on Automatic Control，2002，47(10):1648－1662．

2 陈龙，张孝良，江浩斌，等．基于机电系统相似性理论的蓄能悬架系统［J］．中国机械工程，2009，20(10):1248－1251．CHEN Long，ZHANG Xiaoliang，JIANG Haobin，et al．Vehicle suspension system employing inerter based on electricalmechanical analogy theory［J］．China Mechanical Engineering，2009，20(10):1248－1251．(in Chinese)

3 SHEN Yujie，CHEN Long，YANG Xiaofeng，et al．Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension［J］．Journal of Sound and Vibration，2016，361:148－158．

4 WANG FC，HONG M F，CHEN CW．Building suspensions with inerters［J］．Proc．IMechE，Part C:Journal of Mechanical Engineering Science，2010，224(8):1605－1616．

5 孙晓强，陈龙，汪少华，等．2级串联式ISD悬架非线性建模与参数优化［J/OL］．农业机械学报，2014，45(6):7－13．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?file_no=20140602＆flag=1．DOI:10．6041/j．issn．1000-1298．2014．06．002．SUN Xiaoqiang，CHEN Long，WANG Shaohua，etal．Nonlinearmodeling and parameter optimization of two-stage series-connected ISD suspension［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2014，45(6):7－13．(in Chinese)

6 杨晓峰．基于动力吸振原理的车辆ISD悬架动力学特性与实现方法研究［D］．镇江:江苏大学，2013．YANG Xiaofeng，Research on dynamic characteristics and realization method of vehicle inerter-spring-damper suspension based on dynamic vibration absorbers principle［D］．Zhenjiang:Jiangsu University，2013．(in Chinese)

7 张孝良，聂佳梅，汪若尘，等．基于惯容-弹簧-阻尼结构体系的被动天棚阻尼悬架系统［J/OL］．农业机械学报，2013，44(10):10－14，9．http:∥www．j-csam．org/jcsam/ch/reader/view_abstract．aspx?file_no=20131002＆flag=1．DOI:10．6041/j．issn．1000-1298．2013．10．002．ZHANG Xiaoliang，NIE Jiamei，WANG Ruochen，et al．Passive skyhook-damping suspension system based on inerter-springdamper structural system［J/OL］．Transactions of the Chinese Society for Agricultural Machinery，2013，44(10):10－14，9．(in Chinese)

8 EVANGELOU S，LIMEBEER D，SHARPR，et al．Control ofmotorcycle steering instabilities［J］．IEEE Control Systems，2006，26(5):78－88．

9 SMITH M，WANG F C．Performance benefits in passive vehicle suspensions employing inerters［J］．Vehicle System Dynamics，2004，42(4):235－257．

10 WANG F C，HONG M F，LIN T C．Designing and testing a hydraulic inerter［J］．Proc．IMech E，Part C:Journal of Mechanical Engineering Science，2011，225(1):66－72．

11 聂佳梅，张孝良，江浩斌，等．惯容器模型结构探索［J］．机械设计与研究，2012，28(1):29－32．NIE Jiamei，ZHANG Xiaoliang，JIANG Haobin，et al．Research on the inerter structure［J］．Machine Design and Research，2012，28(1):29－32．(in Chinese)

12 SWIFT S，SMITH M，GLOVER A，et al．Design and modeling of a fluid inerter［J］．International Journal of Control，2013，86(11):2035－2051．

13 WANG F C，CHAN H A．Vehicle suspensionswith amechatronic network strut［J］．Vehicle System Dynamics，2011，49(5): 811－830．

14 张孝良，聂佳梅．摩擦力对滚珠丝杠惯容器频响特性的影响［J］．机械科学与技术，2015，34(5):770－774．ZHANG Xiaoliang，NIE Jiamei．Influence of the friction force on the frequency response characteristics of ballscrew inerter［J］．Mechanical Science and Technology for Aerospace Engineering，2015，34(5):770－774．(in Chinese)

15 PAPAGEORGIOU C，SMITH M．Laboratory experimental testing of inerters［C］∥Proceedings of the 44th IEEE Conference on Decision and Control，and the European Control Conference，2005:3351－3356．

16 孙晓强，陈龙，汪若尘，等．滚珠丝杠式惯容器试验及力学性能预测［J］．振动与冲击，2014，33(14):61－65，83．SUN Xiaoqiang，CHEN Long，WANG Ruochen，et al．Experiment and mechanical properties prediction on ball-screw inerter［J］．Journal of Vibration and Shock，2014，33(14):61－65，83．(in Chinese)

17 SUN X Q，CHEN L，WANG SH，etal．Performance investigation of vehicle suspension system with nonlinear ball-screw inerter［J］．International Journal of Automotive Technology，2016，17(3):399－408．

18 HU Yinlong，CHEN M Z Q，XU Shengyuan，et al．Semiactive inerter and its application in adaptive tuned vibration absorbers［J］．IEEE Transactions on Control Systems Technology，2017，25(1):294－300．

19 PIRESL，SMITH M，HOUGHTON N E，etal．Design trade-offs for energy regeneration and control in vehicle suspensions［J］．International Journal of Control，2013，86(11):2022－2034．

20 ZHU D，LIU Y，WEN J．A simulation research of the mechatronic inerter based on active control［C］∥IEEE International Conference on Information and Automation，2015:1269－1272．

Design and Characteristics Analysis of Ball Screw Type Inerter w ith Planetary Flywheel

GE Zheng WANGWeirui
(College of Mechanical Engineering，Zhejiang University，Hangzhou 310027，China)

The inerter can replace the mass block and realize the dynamic characteristic of large inertia body with small mass，thus greatly enriching the design theory of mechanical vibration network．To achieve the same inertance，the larger the inertia-mass ratio is，the lighter the mass of the flywheel is，and the advantage ismore obvious．In order to improve the inertia-mass ratio of ball screw type inerter，a new design of ball screw type inerterwith planetary flywheelwas put forward．By themechanicalmodel of inerter，the influence of structure parameters on the inertia-mass ratio of flywheelwas researched．Result showed that the inertia-mass ratio could be improved by three methods:increasing the number or thickness of the planet gears，reducing the pin diameter，which increased the proportion of planet gear rotation inertia in the total inertia of flywheel．Themaximum inertia-mass ratio could be obtained by the optimal gear ratio of planet gear to ring gear，which was calculated by the number and thickness of planet wheel and the pin diameter．Themechanical properties of planetary flywheel inerter were compared with those of traditional inerter．Analysis of result indicated that the inertia-mass ratio of planetary flywheel inerter was larger than that of traditional inerter with the same diameter of flywheel．But for the same radial size，the planetary flywheel was thicker than the traditional single flywheel．Therefore，the planetary flywheel inerter was suitable for the weight sensitive，and the axial space-rich application occasions．The theoretical analysiswas verified by experiment at last．

inerter;planetary flywheel;ball screw;inertia-mass ratio

O313;TH113

A

1000-1298(2017)07-0391-08

2016-09-13

2017-01-10

国家自然科学基金项目(51005206)

葛正(1986—)，男，博士生，主要从事车辆零部件试验技术研究，E-mail:gezheng01@126．com

王维锐(1978—)，男，高级工程师，主要从事车辆工程和汽车零部件测试方法研究，E-mail:wwrzju@126．com

10．6041/j．issn．1000-1298．2017．07．050