机械臂轨迹规划中的奇异规避及位置补偿研究

储一萌，樊留群

(同济大学 中德学院，上海 201800)



机械臂轨迹规划中的奇异规避及位置补偿研究

储一萌，樊留群

(同济大学 中德学院，上海 201800)

为了保证机械臂高精度的奇异规避轨迹规划，提出一种对于球形腕部机械臂的避奇异方法——阻尼倒数+非奇异方向补偿算法(damped reciprocal plus compensations in non-singular directions, DRPCIND)。首先针对实验机械臂提出阻尼倒数原理；然后分析机械臂的三种奇异方向；最后在奇异区将非奇异方向补偿与阻尼倒数算法相结合，为了回归至理想轨迹，在非奇异区应用平滑补偿算法。通过与原阻尼倒数法进行实验对比，不仅证明该算法在奇异规避中的有效性，而且在平移和/或转动运动中具有更高的轨迹规划精度。

机械臂；奇异性；阻尼倒数；非奇异方向；位置补偿

0 引言

当机械臂在用户空间进行轨迹规划时，如直线或圆弧插补运动，经常遇到奇异位型，即笛卡儿空间与关节空间的速度关系产生“病态”解，并造成自由度退化[1]，因此经常导致规划失败。

针对奇异问题，阻尼最小二乘法[2-3]和退化方向消除法[4]的发展较为成熟。近年来各学者又有了相关研究，在示教与再现应用中Huang等[5]提出通过点到点的奇异规避算法在经过奇异区时使用关节运动代替末端执行器的平移与旋转运动。另外Choi等[6]利用最小无穷范数的思想也可以有效解决奇异问题。值得注意的是，Xu等[7]提出的阻尼倒数法(damped reciprocal,DR)，因为其与阻尼最小二乘法相比不仅有较好的精度，而且因为无需估算最小奇异值，所以在运算效率上有所提高，故有更好的应用前景。

机械臂在进行高精度位置控制时，上述算法本身就会在奇异区造成误差，加之不针对位置控制，如阻尼倒数法是关于速度关系提出的，所以在转化成位置控制时势必会造成额外的误差，并且在离开奇异区时，也需要相应的算法使其回归到理想轨迹中，然而一直以来对于误差补偿方向却鲜有研究，文献[2]和文献[7]中只进行了简单的方法说明。

所以在如何减小奇异区误差并在轨迹规划中最终消除误差就成为很有研究价值的应用问题。本文在阻尼倒数法的基础上，提出一种高精度规避奇异算法，即阻尼倒数+非奇异方向补偿法(damped reciprocal plus compensations in non-singular directions, DRPCIND)，通过对比试验证明其不仅能够有效避开奇异位型，而且可获得更高的位置插补精度。

1 阻尼倒数原理

本文实验研究对象为具有球型腕部的六自由度机械臂，如图1所示其D-H参数只有a1、a2、a3、d4和d6为非零值。

图1 具有球型腕部机械臂的D-H坐标

(1)

则针对本实验对象的阻尼倒数算法[7]为：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Ssa1+a2c2+a3c23+d4s23

(11)

Sea3s3-d4c3

(12)

Sws5

(13)

当Ss=0和/或Se=0和/或Sw=0时，机械臂处于奇异位型，根据奇异作用范围的不同分别称作肩部奇异、肘部奇异和腕部奇异。其次εx为相应奇异参数的阈值，μx为阻尼系数，μ0为名义阻尼系数。

另外因为腕部坐标系{W}和末端执行器坐标系{E}的联系，故可得以坐标系{E}原点为速度参考点的雅可比矩阵0JE和0JW的转换关系TE→W：

(14)

其中I3×3为3×3单位向量，03×3为3×3的零向量，tE→W为3×3的转换矩阵。

2 误差补偿原理

2.1 奇异方向分析

参考式(1)，在坐标系{2}中表示的腕部坐标系{W}的平移速度2vw为：

(15)

其中，

(16)

当Sc=0或Ss=0时，2J11不满秩，由此可得出机械臂处于奇异位形时的奇异方向为坐标系{2}的x轴和z轴。从运动学角度分析，当机械臂处于肩部奇异时(Ss=0)，腕部坐标系{W}的奇异运动是沿着奇异方向0ρs(坐标系{2}z轴的方向向量)的平移运动。当机械臂处于肘部奇异时(Se=0)，腕部坐标系{W}的奇异运动是沿着奇异方向0ρe(坐标系{2}x轴的方向向量)的平移运动。

同理，参考式(1)，坐标系{5}中表示的腕部坐标系{W}的转动速度5ωw为：

(17)

其中:

(18)

当Sw=0时，2J22不满秩，由此可得出机械臂处于奇异位形时的奇异方向为坐标系{5}的x轴。从运动学角度分析，当机械臂处于腕部奇异时(Sw=0)，腕部坐标系{W}的奇异运动是沿着奇异方向0ρw(坐标系{5}x轴的方向向量)的旋转运动。

根据以上分析可求出各奇异方向0ρx：

0Ps=0R22z，其中2z=[0 0 1]T

(19)

0Pe=0R22x，其中2x=[1 0 0]T

(20)

0Pw=0R55x，其中5x=[1 0 0]T

(21)

2.2 奇异区非奇异方向补偿原理

2.2.1 奇异区平移奇异补偿控制律

平移奇异的特点是奇异发生在平移运动中，而与转动无关。故针对0vw只能进行非奇异方向补偿，而0ωw可进行全方向补偿。

实际应用中在已知末端执行器坐标系{E}运动速度0vE的前提下，可将补偿速度0vw定义如下：

0vw=0vwd+βt0ewtαx

(22)

其中,x=s,e，βt表示平移位置误差补偿放大系数，0vwd表示理想的腕部坐标系{W}平移速度，其由下式计算：

0vwd=It0vw=It(TE→W0vE)

(23)

0ewtαx是投影在与相应奇异方向向量0ρx垂直的平面αx上的腕部坐标系{W}的平移位置误差，其可由下式计算：

0ewtαx=0ewt-0ewtρx

(24)

其中,0ewt表示坐标系{W}的平移位置误差，0ewtρx表示投影在相应奇异方向向量0ρx上的坐标系{W}的平移位置误差。

0ewt与0ewtρx的计算方法如式(25)和(26)所示：

0ewt=It0ew=It(TE→W0eE)

(25)

(26)

其中,0ew与0eE分别表示腕部坐标系{W}的运动误差和末端执行器坐标系{E}的运动误差，0eE的表达式如下：

(27)

式中，0eEt与0eEr分别表示坐标系{E}的平移误差和转动误差。下标a特指末端执行器坐标系{E}的实际值，d特指{E}的理想值。坐标系{E}的原点位置坐标为P，坐标系转动位置通过3×3旋转矩阵[nsa]表示，其中n，s和a都是单位正交向量。另外计算过程中It=[I3×303×3]可提取运动向量的平移分量。

总结式(22)～式(26)，可得出平移奇异0vw的补偿控制律：

对于│Sx│≤εx,x=s,e

(28)

对于速度0ωw补偿，在已知末端执行器坐标系{E}转动速度0WE的前提下，定义如下：

0ωw=0ωwd+βr0ewr

(29)

其中，βr表示转动位置误差补偿放大系数。0ewr是坐标系{W}的转动位置误差。0ωwd是腕部坐标系{W}的理想转动速度。根据腕部坐标系{W}的定义，{W}与{E}的相对位置固定，故0ewr=0eEr，0ωwd=0ωE。因此平移奇异0ωw的补偿控制律：

对于│Sx│≤εx,x=s,e

0ωw=0ωE+βr0eEr

(30)

2.2.2 奇异区转动奇异补偿控制律

与位置奇异不同，转动奇异的特点是奇异发生在转动运动中，而与平移无关。故针对0vw可进行全方向补偿，而0ωw只能进行非奇异方向补偿。

与2.2.1节所述的原理相同，在此不再赘述。在已知末端执行器坐标系{E}运动速度0vE的前提下，转动奇异0vw的补偿控制律：

对于│Sx│≤εx,x=w

0vW=0vwd+βt0ewt=ItTE→W0vE+βtItTE→W0eE

(31)

对于速度0ωw补偿，在已知末端执行器坐标系{E}转动速度0ωE的前提下，可推出转动奇异0ωw的补偿控制律：

对于│Sx│≤εx,x=w

(32)

2.3 非奇异区误差补偿控制律

2.3.1 平滑补偿系数

非奇异区特指离开奇异区至回归期望轨迹这段区间。非奇异区内不仅需要保留非奇异方向的误差补偿控制律，还需要对奇异方向进行平滑的补偿控制以使坐标系{E}回归至理想的笛卡尔轨迹规划中。

为了在奇异方向达到平滑补偿的目的，补偿基函数需要满足一定的条件：

命题:设补偿基函数：

证明：f(x)显然满足地f(0)=0 ,f(1)=1，故满足条件①。

补偿基函数的导数：

显然f′(0)=0,f′(1)=0，也满足条件②，对于∀x对于∀x故即当x=0.5时，函数连续且可导，又对于∀x(0,0.5)∪(0.5,1)，f′(x) >0，故当x(0,1)时，f′(x) >0，即区间内单调递增，又因为f(0)=0，故当x(0,1)时，f′(x) >0，因此条件③满足，证毕。

根据补偿基函数，补偿系数定义如下：

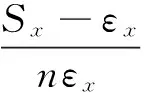
(33)

n为控制补偿范围，ψ为非奇异区误差补偿放大系数。

2.3.2 非奇异区平滑补偿控制律

非奇异区内的平移奇异补偿控制律与2.2.1节所述的原理相同，但需要对奇异方向进行平滑补偿，其定义为：

对于│Sx│>εx,x=s,e

(34)

0ωw=0ωE+βr0eEr

(35)

同理，非奇异区的转动奇异补偿控制律：

对于│Sx│>εx,x=w

0vw=0vwd+βt0ewt=ItTE→W0vE+βtItTE→W0eE

(36)

(37)

3 实验验证

3.1 实验平台

本实验控制系统基于PC平台开发[8]，为了满足高精度与高实时性控制的要求，总线选择具有极佳网络性能和实时性的EtherCAT[1，10-11]，具体系统配置见表1。

表1 控制系统配置

实验中EtherCAT总线的应用层协议为CoE，其通过对象字典来进行相应的运动控制。在位置插补模式中，有两个重要的对象字典，分别是60C2h和60C1h，它们分别负责插补周期的和插补数据的设置。综上所述，在已知起始位置P0、结束位置Pe、运行时间T、插补周期△t、最大线速度Vmax和最大定轴转动速度Ωmax的情况下，通过位置插补模式的笛卡尔坐标系轨迹规划的运动控制系统如图2所示。

图2 笛卡尔坐标系下轨迹规划的运动控制系统

3.2 对比实验

本节通过直线插补运动来验证本文提出的阻尼倒数+非奇异方向补偿的有效性，并且和原阻尼倒数算法(只在非奇异区进行平滑补偿)进行对比，阐述其优势。

因为原理相同，所以本次实验只对转动奇异进行验证。其中非奇异区补偿中，控制补偿范围系数n=2，非奇异区误差补偿放大系数ψ=80。

对于转动奇异，只有腕部奇异一种，设起始位置P0={0.1m,0.9m,1.3m,14.92°,32.77°,-131.98°}，结束位置Pe={-0.1m,1.1m,1.3m,73.90°,76.98°,33.69°}，运行时间T=6s，插补周期Δt=5ms，最大线速度Vmax=0.05m/s，最大定轴转动速度Ωmax=22.918°/s 。平移位置误差补偿系数βt=300，转动位置误差补偿系数βr=100，奇异参数阈值εx=0.07，名义阻尼系数μ0=0.1。图3显示了直接进行逆解运算的仿真结果，不难看出第四和第六轴都在奇异区产生了极大的速度，这在实际运用中是必须避免的。图4对比了运用阻尼倒数以及本文提出的阻尼倒数+非奇异方向补偿进行插补运算的各轴转速，可看出对于腕部奇异本文提出的DRPCIND有很好的避奇异功能，并且从图5以及图6分析可知，虽然平移误差并没有提高，但是转动误差减小了近一倍，说明本文提出的算法对比原有算法有更好的插补精度。

图3 腕部奇异下直接进行逆解规划的关节速度

图4 腕部奇异下利用本文方法和阻尼倒数法规划的关节速度

图5 腕部奇异下利用本文方法和阻尼倒数法规划的平移误差

图6 腕部奇异下利用本文方法和阻尼倒数法规划的转动误差

5 结论

本文研究具有球形腕部的六自由度机械臂高精度奇异规避的控制方法，提出了阻尼倒数+非奇异方向补偿算法。试验结果表明，在与普通的阻尼倒数法相比不仅有有效的规避奇异功能，而且具有更小的平移误差或转动误差。

但是不难看出依然无法摆脱在阻尼规避奇异算法类型中需要手动调参的事实，这直接影响算法的有效性，所以今后的研究重点是如何使系统具有自动调整到最佳参数的功能。

[1] Kim J H, Sun L, Matson E T, et al. Robot Intelligence Technology and Applications 2012[M]. Berlin: Springer Berlin Heidelberg, 2013.

[2] Chiaverini S, Siciliano B, Egeland O. Review of damped least squares inverse kinematics with experiments on an industrial robot manipulator[J]. IEEE Transactions on Control Systems Technology, 1994, 2(2): 123-134.

[3] Phuoc L M, Martinet P, Lee S, et al. Damped least square based genetic algorithm with Ggaussian distribution of damping factor for singularity-robust inverse kinematics[J]. Journal of Mechanical Science and Technology, 2008, 22(7): 1330-1338.

[4] Oetomo D, Jr M H A. Singularity robust algorithm in serial manipulators[J]. Robotics and Computer-Integrated Manufacturing, 2009, 25(1): 122-134.

[5] Huang Y J, Yong Y S, Chiba R, et al. Kinematic Control With Singularity Avoidance for Teaching-Playback Robot Manipulator System[J]. IEEE Transactions on Automation Science & Engineering, 2015, 13(2): 729-742.

[6] Choi H B, Lee S, Lee J. Minimum infinity-norm joint velocity solutions for singularity-robust inverse kinematics[J]. International Journal of Precision Engineering and Manufacturing, 2011, 12(3): 469-474.

[7] Xu W, Liang B, Xu Y. Practical approaches to handle the singularities of a wrist-partitioned space manipulator[J]. Acta Astronautica, 2011, 68(1-2): 269-300.

[8] Moon Y, Ko N Y, Lee K, et al. Real-time EtherCAT Master Implementation on Xenomai for a Robot System[J]. International Journal of Fuzzy Logic & Intelligent Systems, 2009, 9(3):244-248.

[9] Vaezi M, Samavati F C, Jazeh H E S, et al. Singularity analysis of 6DOF Stäubli©TX40 robot[C]// IEEE International Conference on Mechatronics and Automation. Beijing, China:IEEE, 2011: 446-451.

[10] Prytz G. A performance analysis of EtherCAT and PROFINET IRT[C]// IEEE International Conference on Emerging Technologies and Factory Automation. Hamburg, Germany: IEEE, 2008: 408-514.

[11] Choi T, Do H M, Kyung J H, et al. Control of 6DOF articulated robot with the direct-teaching function using EtherCAT[C]// Ro-Man. Gyeongju, Korea: IEEE, 2013: 338-339.

(编辑 李秀敏)

The Study of Avoiding Singularities and Position Compensations towards the Trajectory Planning of Manipulators

CHU Yi-meng, FAN Liu-qun

(Sino-German College, Tongji University, Shanghai 201800, China)

To ensure the high accurate trajectory planning of avoiding singularities of manipulators, a avoiding singularities method, damped reciprocal plus conpensation in non-singular directions(DRPCIND), is proposed for manipulators with spherical wrists. Firstly, for the experimental manipulator the damped reciprocal principle is raised. Then, three singular directions of the manipulator are analyzed. Finally, compensations in non-singular directions are combined with the damped reciprocal algorithm within the singualrity area. In order to return to the desired trajectory, the smooth compensation algorithm is applied without singularity area . Not only is effectiveness of the proposed algorithm in avoiding singularities verified, but also the higher accurate trajectory planning at the translational and/or rotational motion is obtained by experimentally comparing with the original damped reciprocal algorithm.

manipulator; singularity; damped reciprocal; non-singular direction; position compensation

1001-2265(2017)07-0092-05

10.13462/j.cnki.mmtamt.2017.07.022

2017-02-10；

2017-03-08

储一萌(1991—)，男，江苏宜兴人，同济大学中德学院硕士研究生，研究方向为机器人控制系统与轨迹规划，(E-mail)jsxzsrcym@163.com；通讯作者：樊留群(1964—)，男，西安人，同济大学中德学院教授，博士，研究领域为生产过程自动化与机器人技术，(E-mail)lqfan@tongji.edu.cn。

TH165;TG659

A