振动条件下旋流分离器内螺旋流的流固耦合研究

徐 艳, 张彦月, 徐德奎, 袁 粼, 李 森, 王尊策

(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318; 2.大庆油田有限责任公司采油工程研究院,黑龙江大庆 163453)

振动条件下旋流分离器内螺旋流的流固耦合研究

徐 艳1, 张彦月1, 徐德奎2, 袁 粼1, 李 森1, 王尊策1

(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318; 2.大庆油田有限责任公司采油工程研究院,黑龙江大庆 163453)

旋流分离器工作时受到外部流体的影响会产生振动,从而影响内部流场分布规律。为研究振动条件下旋流分离器内螺旋流的流固耦合作用,建立振动条件下旋流分离器的双向流固耦合模型,对同种激振频率下不同激振力的流固耦合作用进行数值模拟。结果表明:螺旋流场随着结构一起运动,而结构的运动引起了流场结构的偏移;周期振动下的流场径向速度变大,并随激振力的增大而增加;周期性激振力影响了切向速度的对称性,并使轴向速度近轴区域速度变大;不同截面的结构运动轨迹呈“O”型,振动形态呈抛物线状。

旋流分离器; 流固耦合; 周期振动; 螺旋流场

旋流分离器作为分离设备广泛应用于石油石化领域,在其实际工作时,常将多根并联在一个大的罐体中共同工作,以提高其处理能力。来流从罐体入口流入,流经旋流器,在其外壁形成圆柱绕流,进而产生涡激振动。设备的振动引起内部螺旋流场产生振荡,而振荡又进一步作用于设备,产生流固耦合作用。近年来流固耦合的研究主要集中在分域耦合的顺序或同步迭代耦合上。Hirt等[1]提出了ALE描述法,实现了固体力学中Lagrange描述格式和流体力学中Euler描述格式的统一。周岱等[2]在压力Poisson方程中引入质量源项,发展了一种基于ALE描述有限元法的弱耦合分区算法。Wulf 等[3]模拟流固耦合问题时,研究了流体流动和网格运动耦合的影响。Jaiman等[4]利用有限体积法求解流体域,有限元法求解结构域,在流体-结构界面处采用不匹配网格划分,提出了结合界面边界条件法补偿弱耦合过程中时间滞后问题。He 等[5]基于 ALE 有限元方法求解了多种钝体流固耦合问题,详细分析了系统物理参数对结构响应和流场特征的影响。冯志鹏等[6]基于有限体积法和有限元法,结合动网格控制技术,计算了流体力与结构位移间的相位关系。裴吉等[7-8]采用双向同步求解的方法研究了叶轮流固耦合作用对离心泵内部流场的影响。胥锋[9]通过ANSYS Workbench平台进行流固耦合仿真,得到了泵腔内流体的流动形态和流速分布情况。谭越等[10]基于单向流固耦合分析技术,计算得到了涡轮结构的变形和应力分布情况。王维忠等[11]利用FLUENT软件对斜管组油水分离装置内的流场分布进行模拟,结合Workbench流固耦合技术计算了流体作用下装置的变形和应力分布。谢超[12]运用ANSYS软件对气液两相流典型管段进行模态分析和动力学计算,提出一些两相流管道减振设计措施。邱亚东等[13]采用双向耦合隐式算法,研究了无支撑和有支撑情况下水力旋流器的振动特性。李森等[14]对水力旋流器在自激振动条件下的耦合流场进行数值模拟研究。目前国内外学者研究了流固耦合对圆管内外流场和叶轮结构可靠性的影响,但对周期振动旋流分离器变径圆管内螺旋流场的流固耦合研究及振动周期内不同相位的流场和结构变化规律研究比较少。笔者建立振动条件下旋流分离器内螺旋流的流固耦合模型,研究周期性振动对旋流分离器内螺旋流场和结构变形及时程响应的影响规律。

1 计算建模和算法

1.1 流场计算模型与算法

1.1.1 流体域控制方程

质量守恒方程:

(1)

式中,ρ为流体密度,kg/m3;uj为速度在坐标方向的分量,其中j=1,2,3。

动量守恒方程:

(2)

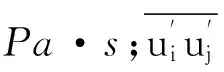
采用雷诺应力模型(RSM)对控制方程进行封闭。

1.1.2 几何模型和算法

流体域选用主直径D=28mm的双锥水力旋流器,其结构简图见图1。入口深度、宽度和长度分别为:a=0.68D,b=0.7D,c=2.56D,溢流嘴直径Du=0.28D,底流直径Dd=0.5D,旋流腔长度h1=D,大椎段长度h2=1.42D,小锥段长度h3=9.55D,尾管长度h4=10.18D,大椎角α=20°,小锥角θ=1.5°。流体介质为水,入口为速度入口,底流和溢流为自由出流,设定分流比为5%,非耦合情况为标准壁面函数,耦合情况为耦合界面。采用有限体积法对控制方程进行离散,SIMPLEC算法对压力和速度进行耦合,PRESTO方法对压力项进行离散。动量方程的离散采用具有三阶精度的QUICK格式,湍动能和耗散率的采用二阶迎风格式,雷诺应力采用一阶迎风格式[15]。

图1 旋流器结构简图Fig.1 Schematic diagram for hydrocyclone geometry

1.1.3 网格划分及无关性计算

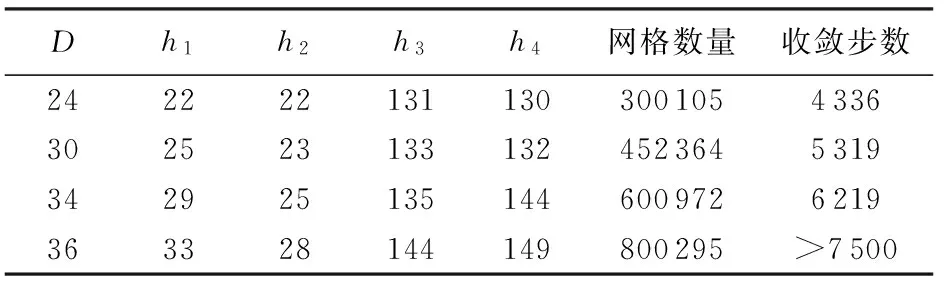
采用ICEM16.0进行网格划分,流体域的网格见图2。为在满足计算精度的条件下减少计算时间,根据稳态流场进行了网格无关性分析。对各部分逐渐加密,如表1所示。

对4种网格分别进行稳态求解,取各自收敛时的速度进行比较。S3截面处的无量纲切向速度如图3(图中，Utan和Uin分别为切向和入口速度，m/s;r为径向距离，m;R为该截面管段半径，m)所示。

由图3可以看出,随着网格数增加,最大切向速度逐渐增大,当网格数为600 972时,与网格数为800 295时的误差为1.2%,故选用数量为600 927的网格进行模拟。

图2 流体域网格划分Fig.2 Meshed hydrocyclone geometry in fluid domain

Dh1h2h3h4网格数量收敛步数242222131130300105433630252313313245236453193429251351446009726219363328144149800295>7500

图3 不同网格S3截面的切向速度Fig.3 Tangential velocity profiles with different grid on S3 section

1.2 固体域计算方法

利用有限元方法对结构进行离散,结构在内部流体和外部激振力共同作用下振动,变径圆管的运动方程可表示为

(3)

结构单元为solid186,结构两端为固定端约束,采用Newmark时间积分求解瞬态动力学方程。

1.3 流固耦合算法

采用Ansys Workbench16.0建立 Fluent+Transient structural流固耦合模型,运用交错迭代式耦合求解的计算方法,进行流固耦合数值模拟。流体域和固体域的控制方程在界面处满足位移协调和力平衡条件。对结构施加正弦周期性激振力,同时流体将壁面上的压力载荷传递给结构,结构根据动力学运动方程求解激振力和流体载荷共同作用下的变形,再将位移传递给流体;采用ALE方法动网格方法处理耦合界面边界的运动,动网格运用Smoothing、Layering和Remeshing方法进行重构,设定弹簧弹性系数为0.6,耦合面的网格高度为3 mm;流体采用新的边界条件计算流场,并得到新的沿壁面的压力分布,实现流固耦合计算。

1.4 计算方法验证

为证明本文模拟方法的可靠性,使用比利时LMS公司24通道SCADAS Mobile数据采集系统对旋流分离器进行振动测试,在外流体形成绕流的S4截面,通过扫频信号源控制激振器的激振力和激振频率,对结构沿着Y轴方向施加正弦周期性激振力。应用PCB公司ICP型加速度压电式传感器,采用LMS Test. Lab软件进行数据分析,取5次测量的平均结果,得到了振动耦合效应下旋流分离器轴向各点加速度,试验装置见图4。试验结构采用不锈钢347,模拟参数与试验一致,具体参数见表2。

图4 旋流器振动测试试验实物照片Fig.4 Picture of vibration test experiment with hydrocyclone

材料密度/(kg·m-3)弹性模量/GPa泊松比激振频率/Hz激振力/N处理量/(m3·h-1)入口速度/(m·s-1)不锈钢34779101900.317.522.21022451.511.89有机玻璃118030.3472020/50/10031.13

处理量为4 m3/h和5 m3/h时,旋流器轴向8个测点最大加速度的实测结果和数值模拟结果如图5所示。由图5可以看出,模拟结果和实测结果吻合较好,故本文中选用的流固耦合模型较为可靠。

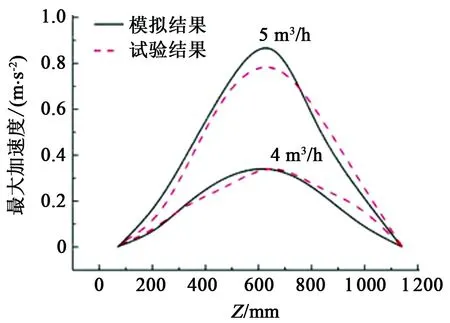
图5 不同处理量时的实测和模拟结果Fig.5 Results between measure and simulation at different flow rate

2 计算结果及对比分析

设定流体处理量为3 m3/h,激振方向为Y轴,激振位置为S4,具体参数见表2。振动周期为0.05 s,时间步长为0.006 25 s,观察2 s后流动稳定状态下,一个振动周期内流场以及结构的变化情况。t1～t9分别对应从2～2.05 s,时间间隔为0.006 25 s的时间节点。激振力作用下结构的最大变形在S6截面,故选S6截面分析,结构沿Y轴方向的位移变化见图6。从图6中可以看出,不同激振力下位移均呈周期性变化,正负向位移的周期对称性很好,但相位有所变化,随着激振力增大,位移量增大,周期有滞后的趋势。

图6 S6截面一个振动周期内的位移变化Fig.6 Displacement in one vibrational period on S6 section

2.1 50N激振力下不同截面位置的速度对比

对激振力为50 N时进行分析,对比了t3时刻Y轴方向的无量纲瞬时速度,如图7所示。由图7可以看出,瞬时速度从壁面处随半径的减小而增加,存在最大速度点,之后随半径的减小而减小。各截面瞬时速度轴心发生了偏移,S6截面偏移量最大,偏移量与结构位移一致,此时速度的不对称性也最明显。这表明螺旋流场不仅随着结构一起运动,而且结构运动引起了流场结构的偏移。S6截面流场速度轴心偏移最大,故选取此截面进一步分析。

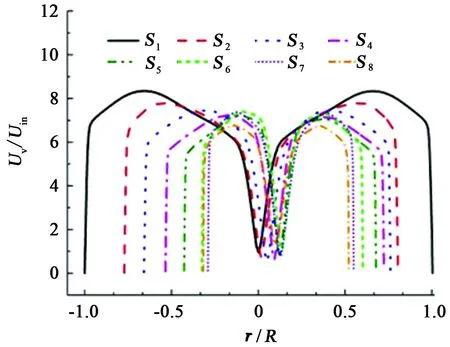
图7 t3时刻不同截面的瞬时速度Fig.7 Instantaneous velocity of different section on time t3

2.2 一个振动周期内的速度分析

2.2.1Y轴方向速度分布

激振力为50N时,一个振动周期内S6截面Y轴方向轴向速度、径向速度和切向速度见图8。

不同时刻S6截面轴向速度最大值基本相同,但其轴心沿Y轴正负向摆动。轴向速度整体对称性较好,但在一个振动周期内t2和t4时刻,t1和t5时刻,t6和t8时刻的速度不完全重合,t1和t9时刻速度完全重合,说明流体振动的周期与施加激振力的周期一致,但在一个振动周期内存在一定的相位偏差。

不同时刻S6截面径向速度数值较小,受到周期性激振力的影响波动明显。传统旋流器径向速度为流体从边壁向中心运移,而激振力作用直接改变了径向速度的分布,使得径向速度运动与结构相似,但由于流体的耦合作用使速度值不同。在轴心位置出现了不对称现象,这是由于轴向速度和切向速度变化引起的。

不同时刻S6截面切向速度变化规律与轴向速度相似,切向速度涡心随结构的振动沿Y轴正负向摆动。但从t2～t4和t6～t8时刻切向速度出现了不对称现象,此时径向速度也存在不对称现象。

2.2.2 X轴方向速度分布

激振力为50N时,一个振动周期内S6截面X轴方向轴向速度、径向速度和切向速度见图9。

不同时刻S6截面X轴方向的轴向速度基本无偏移,说明激振力没有直接影响X轴方向的轴向速度分布,但近轴区域轴向速度,t2时刻向下流动趋势增加。这是因为,此时结构向Y轴正方向偏移,轴向拉长,向下流动的液量增加,轴向速度增大。t3时刻向下流动趋势进一步增加,达到近轴区的最大值。t5时刻回到平衡位置与t1时刻重合。

不同时刻S6截面X轴方向的径向速度变化程度较大,比Y轴方向的径向速度大1个数量级,尤其在轴心位置达到峰值,说明此处流体发生了较为剧烈的径向运移,这种移动在t2～t4和t6～t8时刻最为显著。这是因为,振动使得流体向下流动的趋势增大,加快流体向中心运移,使径向速度增大。

不同时刻X轴方向的切向速度轴心位置未发生明显变化,但切向速度数值发生了明显变化,且不对称性最为显著,t1、t5和t9时刻流场的切向速度在单侧达到最大值。t3和t7时刻在单侧达到最小值。这是由于X轴切向速度与结构Y轴运动方向平行,当X轴切向速度与结构运动方向一致时,形成加速,反之减速,引起了切向速度在平衡位置的不对称。

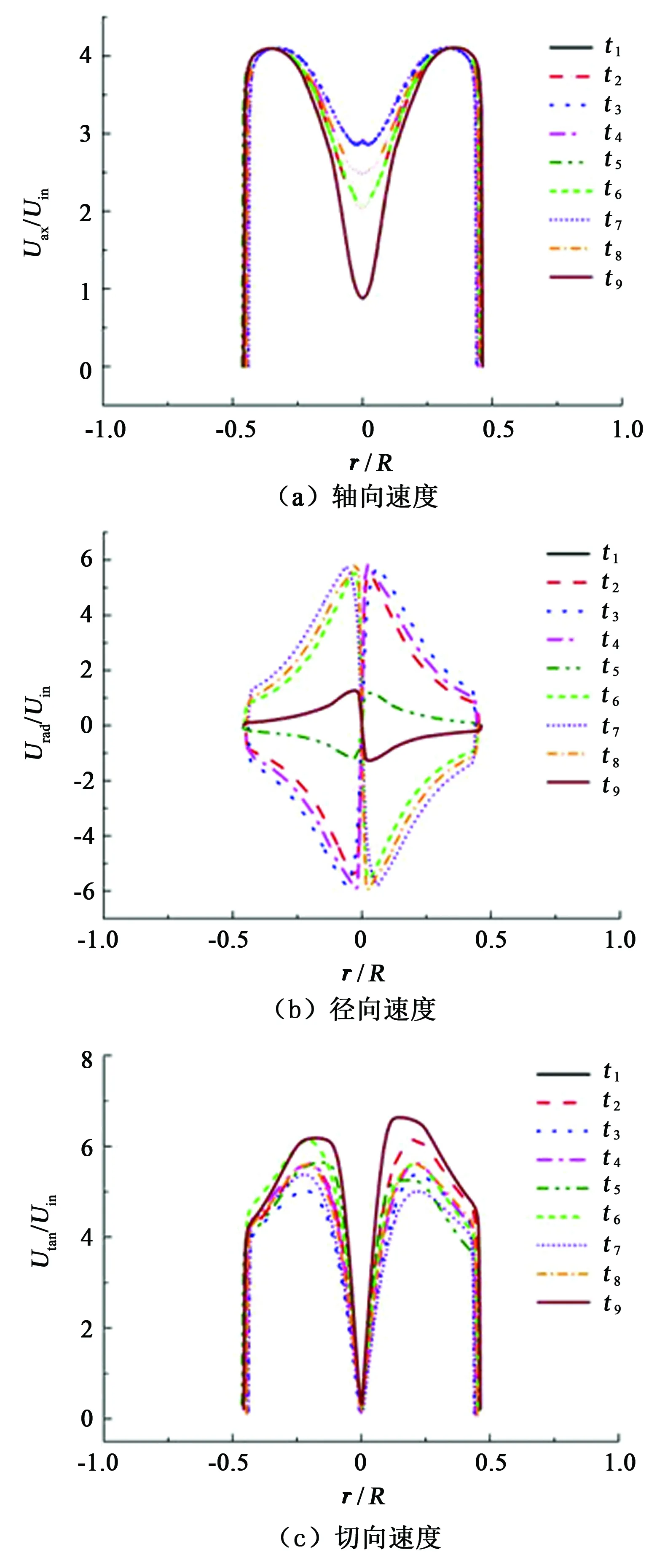
图9 50 N激振力下S6截面X轴方向速度Fig.9 Velocity along X axial direction at 50 N strength on S6 section

2.3 不同激振力下流场速度对比

2.3.1 Y轴方向速度分布

t1时刻不同激振力下S6截面Y轴方向轴向速度、径向速度和切向速度对比如图10所示。

不同激振力下S6截面Y轴方向的轴向速度最大值基本相同。轴向速度整体有所偏移,近轴区域耦合流场轴向速度小于非耦合流场。随着激振力的增加,向Y轴负方向偏移量增大,流体向下运移量增加,轴向速度增大。

不同激振力下S6截面Y轴方向的径向速度受不同激振力的影响较明显,非耦合流场径向速度向轴心移动,速度较小,激振力耦合流场,径向速度整个截面随着结构的同向运动,随激振力增大,径向速度逐渐增加。

不同激振力下对S6截面Y轴切向速度数值和分布没有太大的影响,整体也发生了偏移,偏移方向与轴向速度基本一致,且对称性变差,流场发生了一定程度的摆动,随着激振力的增大,不对称性更为显著。

图10 不同激振力下S6截面Y轴方向速度对比Fig.10 Velocity along Y axial direction at different strength on S6 section

2.3.2 X轴方向速度分布

t1时刻不同激振力下S6截面X轴方向轴向速度、径向速度和切向速度对比如图11所示。

不同激振力下S6截面的X轴方向的轴向速度最大值基本相同,轴向速度未发生摆动,3种激振力下外涡流区轴向速度基本重合,只是内涡流区速度随着激振力的增大逐渐增大,说明激振力增大使流场向下流动的趋势增加。

不同激振力下S6截面X轴方向的径向速度受不同激振力的变化较为明显,随激振力的增大而增加。切向速度受不同激振力影响较大。周期性激振力越大,不对称性越明显。

2.4 结构的时程响应

图12为1 s内不同激振力下S6截面Y方向的加速度时程曲线。由图12中可以看出,在振动初期时程曲线有所波动,这是由于结构激振方向为Y轴方向,而流场入口方向为X轴方向,振动初期时流场运行尚未稳定,从而导致结构在Y轴方向发生波动。1 s时结构振动稳定。

2.5 结构的运动轨迹

为了更直观地展示不同激振力下旋流分离器的振动情况,取计算稳定后的1～2 s时间内进行分析,S2、S4、S6和S8截面的运动轨迹见图13。所截取时间段内的多个振动周期的运动轨迹基本重合。结构在Y轴方向受周期性激振作用,变形明显。流场的耦合作用使X轴方向发生微小变形,结构运动轨迹呈不规则的“O”型。

图13 旋流分离器不同高度轨迹及立体轨迹Fig.13 Motion tracks with different section of hydrocyclone

2.6 结构的振动形态

图14为t1～t9时刻旋流分离器X轴方向和Y轴方向的振动形态图。

图14 旋流分离器的振动形态图Fig.14 Vibration shape of hydrocyclone

旋流分离器的振动形态为抛物线状,不同高度位置的振动基本是同步的。旋流分离器Y轴方向的振动主要由激振力引起,振动规律基本与激振力方向一致,在平衡位置摆动较小,振幅最大时摆动幅度最大。旋流分离器X轴方向的振动主要由流体的冲击力而产生,振动对X轴方向的径向速度产生了较大变化,使得平衡位置时摆动幅度最大,而振幅最大时摆动幅度最小。

3 结 论

(1)流体振动的周期与激振力一致,但在振动周期内存在相位偏差。Y轴方向轴向速度和切向速度沿正负向摆动,径向速度运动规律与结构运动规律相似,但速度值不同。X轴方向近轴区域的轴向速度和径向速度增大,切向速度受到扰动,不对称性明显。激振力的作用使流场发生了变化,3个方向速度互相影响。

(2)不同激振力对轴向速度影响较小,径向速度影响最大,随激振力的增大而明显增大。X轴方向的切向速度随激振力增大不对称摆动幅度增大。

(3)结构运动轨迹呈不规则的“O”型。结构的振动形态为抛物线状,Y轴方向的摆动远大于X轴方向。Y轴方向上,旋流分离器平衡位置时,结构的摆动幅度最小,振幅最大时结构的摆动幅度最大,X轴方向与之相反。

[1]HIRTGW,AMSDENAA,COOKJL.AnarbitraryLagrangian-Euleriancomputingmethodforallflowspeeds[J].JCompPhys, 1974,14(3):227-253.

[2] 周岱,何涛,涂佳黄.流固耦合分析的一种改进CBS有限元算法[J].力学学报,2012,44(3):494-504. ZHOU Dai,HE Tao,TU Jiahuang. An improved CBS finite element method of fluid-structure interaction analysis[J]. Journal of Mechanics, 2012,44(3):494-504.

[3] WULF G D, DJORDJE P. On the coupling between fluid flow and mesh motion in the modelling of fluid-structure interaction[J]. Computational Mechanics, 2008,43(1):81-90.

[4] JAIMAN R, GEUBELLE P, LOTH E, et al. Combined interface boundary condition method for unsteady fluid-structure interaction[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200(1/4):27-39.

[5] HE T, ZHOU D, BAO Y. Combined interface boundary condition method for fluid-rigid body interaction[J]. Computer Methods in Applied Mechanics and Engineering, 2012,223:81-102.

[6] 冯志鹏,臧峰刚,张毅雄.三维横向流体诱发直管振动的数值模拟[J].应用数学和力学,2013,34(12):1311-1320. FENG Zhipeng, ZANG Fenggang, ZHANG Yixiong. Numerical simulation of three-dimensional lateral fluid induced straight pipe vibration[J]. Applied Mathematics and Mechanics, 2013,34(12):1311-1320.

[7] 裴吉,袁寿其,袁建平.流固耦合作用对离心泵内部流场影响的数值计算[J]. 农业机械学报,2009,40(12):107-112. PEI Ji,YUAN Shouqi,YUAN Jianping. Numerical calculation of fluid-structure coupling affect on internal flow field in a centrifugal pump[J]. Journal of Agricultural Machinery, 2009,40(12):107-112.

[8] 裴吉.离心泵瞬态水力激振流固耦合机理及流动非定常强度研究[D]. 镇江: 江苏大学, 2013. PEI Ji. The research of fluid-structure interaction mechanism of transient hydraulic vibration and the unsteady flow intensity of centrifugal pump[D]. Zhenjiang: Jiangsu University,2013.

[9] 胥锋.压电泵的流固耦合仿真分析及试验研究[D]. 长春:吉林大学,2015. XU Feng.The fluid-solid coupling of simulation analysis and experimental research of piezoelectric pump[D]. Changchun: Jilin University, 2015.

[10] 谭越,马文星,卢秀泉.基于流固耦合的冲焊型液力变矩器焊接强度分析[J]. 吉林大学学报(工学版), 2013,43(4):928-932. TAN Yue, MA Wenxing, LU Xiuquan. The welding strength analysis of welding type hydraulic torque converter based on the fluid-structure interaction[J]. Journal of Jilin University (Engineering Science), 2013,43(4):928-932.

[11] 王维忠,仝兴华,闫立志,等.斜管组油水分离装置的结构优化研究[J]. 中国石油大学学报(自然科学版),2015,39(1):122-127. WANG Weizhong, TONG Xinghua, YAN Lizhi, et al. The structure optimization research of oil-water separation devices of inclined tube group[J]. Journal of China University of Petroleum(Edition of Natural Science), 2015,39(1):122-127.

[12] 谢超.气液两相流管道振动特性研究[D].青岛:中国石油大学,2010. XIE Chao. The vibration characteristic research of gas-liquid two phase flow pipeline[D].Qingdao: China University of Petroleum,2010.

[13] 邱亚东,王尊策,李翠艳,等. 流固耦合效应下水力旋流器变径圆管振动特性研究[J]. 化工机械,2015,42(2):240-244. QIU Yadong,WANG Zunce,LI Cuiyan,et al. Study on vibration characteristics of hydrocyclone reducing pipe based on fluid-solid couping[J]. Chemical Machinery, 2015,42(2):240-244.

[14] 李森,张健,王尊策,等.流固耦合作用下水力旋流器内流场的数值模拟[J]. 化工机械,2015,42(5):706-710. LI Sen, ZHANG Jian, WANG Zunce, et al. Numerical simulation of hydrocyclones inner flow field under fluid structure interaction[J]. Chemical Machinery, 2015,42(5):706-710.

[15] KHAIRY E, CHRIS L. The effect of cyclone vortex finder dimensions on the flow pattern and performance using LES[J].Computers & Fluids,2013, 71:224-239.

(编辑 沈玉英)

Study on fluid-structure interaction in hydrocyclone under vibration

XU Yan1, ZHANG Yanyue1, XU Dekui2, YUAN Lin1, LI Sen1, WANG Zunce1

(1.MechanicalScientificandEngineeringinCollegeofNortheastPetroleumUniversity,Daqing163318,China;2.OilProductionEngineeringResearchInstituteofDaqingOilfieldCompanyLimited,Daqing163453,China)

The hydrocyclone is affected by the external fluid and can produce vibration, resulting to the changing the distribution of internal flows. To study the fluid-solid coupling effect of spiral flow in hydrocyclones under the condition of vibration, the two-directional fluid-structure coupling model with the same vibration frequency is established, where the fluid-structure coupling effect of different exciting forces is simulated.The results show that the spiral flow field moves together with the structure, and the motion of the structure causes the migration of the flow field.The radial velocity of the flow field in the periodic vibration becomes larger, and increases with the increase of the exciting force. The periodic exciting force affects the symmetry of the tangential velocity, and makes the axial velocity near the axial become larger. The trajectory of different cross sections of the structure takes the "O" type, and the vibration shape is parabolic.

variable diameter circular tube; fluid-structure interaction; periodic exciting force; spiral flow field

2016-12-20

国家青年科学基金项目(11402051)；黑龙江省青年科学基金项目(QC2016003)

徐艳(1978-)，女，副教授，博士，研究方向为流体机械及工程。E-mail：zhfxuyan@163.com。

王尊策(1962-)，男，教授，博士，研究方向为石油石化流体设备内流特性。E-mail：wangzc@nepu.edu.cn。

1673-5005(2017)04-0140-08

10.3969/j.issn.1673-5005.2017.04.018

TQ 051.8

A

徐艳,张彦月,徐德奎,等.振动条件下旋流分离器内螺旋流的流固耦合研究[J]. 中国石油大学学报(自然科学版), 2017,41(4):140-147.

XU Yan, ZHANG Yanyue, XU Dekui, et al. Study on fluid-structure interaction in hydrocyclone under vibration [J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(4):140-147.

f the tangential velocity, and makes the axial velocity near the axial become larger. The trajectory of different cross sections of the structure takes the "O" type, and the vibration shape is parabolic.

variable diameter circular tube; fluid-structure interaction; periodic exciting force; spiral flow field

2016-12-20

国家青年科学基金项目(11402051)；黑龙江省青年科学基金项目(QC2016003)

徐艳(1978-)，女，副教授，博士，研究方向为流体机械及工程。E-mail：zhfxuyan@163.com。

王尊策(1962-)，男，教授，博士，研究方向为石油石化流体设备内流特性。E-mail：wangzc@nepu.edu.cn。

1673-5005(2017)04-0140-08

10.3969/j.issn.1673-5005.2017.04.018

TQ 051.8

A

徐艳,张彦月,徐德奎,等.振动条件下旋流分离器内螺旋流的流固耦合研究[J]. 中国石油大学学报(自然科学版), 2017,41(4):140-147.

XU Yan, ZHANG Yanyue, XU Dekui, et al. Study on fluid-structure interaction in hydrocyclone under vibration [J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(4):140-147.