磁场对激波冲击R22重气柱作用过程影响的数值模拟*
林震亚,张焕好,陈志华,刘 迎
(南京理工大学瞬态物理国家重点实验室,江苏南京210094)
磁场对激波冲击R22重气柱作用过程影响的数值模拟*
林震亚,张焕好,陈志华,刘 迎
(南京理工大学瞬态物理国家重点实验室,江苏南京210094)
为研究平面入射激波与磁化R22重质圆形气柱的作用过程,首先通过数值方法得到了不同初始条件下激波诱导R22气柱的Kelvin-Helmholtz(KH)及Richtmyer-Meshkov(RM)不稳定性导致的重气柱变形过程,并详细讨论了不同情况下透射激波在气柱内聚焦诱导射流的过程;然后在加入磁场的情况下,采用CTU+CT算法进行数值模拟,以保证数值结果满足任意时刻磁场的散度为零。计算结果表明:磁场对激波诱导R22气柱不稳定性具有抑制作用;法向磁场和流向磁场都可以很好地抑制RM不稳定性;对于KH不稳定性,法向磁场的控制效果更好,不仅可以抑制界面上涡串的卷起,还可以阻止主涡的发展,而流向磁场做不到后者;磁场对射流影响不大,射流处的磁能量可以一定程度上抑制射流的衰减,同时法向磁场可以减小聚焦时压力及速度峰值。
磁化气体;磁流体动力学;磁场;不稳定性;激波
激波与两种不同密度气体界面相互作用时,会在界面附近发生反射、折射及绕射等现象,同时在界面处还会产生Richtmyer-Meshkov(RM)和Kelvin-Helmholtz(KH)不稳定性,导致界面扭曲变形。该现象广泛存在于超燃冲压发动机中的燃料混合、惯性约束核聚变、水中炸药爆炸及天体物理中的超新星爆炸等领域,因而具有重要的研究价值。
目前,对激波与气体界面相互作用的研究主要集中以下两方面:一是气体界面在RM不稳定性与KH不稳定性作用下的演变过程及其相关复杂流动机理;二是界面演化后期的失稳、破碎及湍流混合问题。K.A.Meyer等[1]对激波与气体界面作用时的RM不稳定性进行了数值模拟,得到了与Meshkov实验定性一致的结果;Q.Zhang等[2]研究了二维和三维初始扰动的发展过程,得到了气泡、尖钉速度及界面发展的总体增长率的计算公式;N.N.Anuchina等[3]对初始扰动幅度下相同入射强度激波与正弦扰动气体界面的作用过程进行了数值模拟,结果表明三维数值计算得到的扰动增长率高于二维结果;G.A.Ruev等[4]对马赫数为3.5的平面入射激波与正弦扰动气体界面的作用过程进行了数值模拟,给出了气体界面RM不稳定性的发展过程及两种气体混合区的宽度变化;J.H.J.Niederhaus等[5]对不同强度平面入射激波与多种不同介质的气柱、气泡相互作用过程进行了大量的数值研究,重点分析了作用过程中流场环量的变化和两种气体的混合机理;同时,B.Thornber等[6]对低马赫数的平面入射激波与R22方柱作用过程的数值模拟,结果与Holder等的实验结果完全相吻;B.Hejazialhosseini等[7]对不同马赫数下平面入射激波与氦气气泡作用过程进行了数值研究,得到了气泡的变形过程及气泡表面在KH不稳定作用下次级涡的产生过程;O.Schilling等[8]采用数值方法研究了平面入射激波与Air/R22气体界面的相互作用过程,并分析了反射激波与分界面作用前后流场结构和混合层演变;B.Tian等[9]利用ALE(arbitrary Lagrangian-Eulerian)和GALE(global arbitrary Lagrangian-Eulerian)方法对多种激波与气体界面作用问题进行了数值模拟;S.K.Shankar等[10]采用数值方法模拟了平面入射激波与重气柱作用过程,结果表明流场初始压力和密度梯度是影响两个主涡产生的关键因素;C.Bailie等[11]对不同强度平面入射激波与Air/R22正弦小扰动界面的作用过程进行了数值模拟,并分析入射激波强度对作用过程的影响。
目前,对界面RM不稳定性控制方法的研究表明,合适的磁场对气体界面RM不稳定性的产生与发展具有一定的抑制作用,但仍处在理论研究阶段。S.Chandrasekhar等[12]和V.Wheatley等[13-14]采用线性理论方法推导了垂直或平行于界面的磁场对不可压缩流体界面不稳定性的影响,结果表明:平行于界面的磁场能够抑制RT和RM不稳定性;但是在线性理论下,平面流场中的RM不稳定性与垂直于平面的磁场无关,与实际情况不符。为进一步研究磁场效应,M.Khan等[15]在势流理论的基础上建立了新模型,发现考虑非线性效应后,磁场能够影响界面不稳定性的发展。J.Cao等[16]同时考虑了初始平行于界面的磁场和剪切流对界面不稳定性的影响,发现磁场能够抑制界面不稳定性,而剪切流将会促进界面不稳定性的发展,两者之间存在竞争机制。M.S.Shin等[17]对不同方向磁场作用下,平面激波与球形气泡相互作用过程进行了数值模拟,发现在发展初期,磁场效应很小,而在发展后期,即使是弱磁场,其对界面形状的影响也很明显。此外,磁场越强,界面内外物质混合率越低,并越能抑制后期湍流的发展。李源等[18]基于理论分析的方法,综合考虑黏性和表面张力的影响,考察了磁场中非理想流体中RT不稳定性气泡的演化过程,并推导出描述二维非理想磁流体RT不稳定性气泡运动的控制方程组,得到了流体黏性、表面张力和磁场对气泡界面不稳定性发展的影响。
综上所述,目前对磁场控制不稳定性的研究主要集中在基于不可压理想磁流场的解析推导及磁场影响下所产生现象的数值模拟两个方面。本文中,基于磁流体动力学(magneto-hydro-dynamics,MHD)方程,采用CTU+CT算法对激波冲击磁化R22气柱进行数值模拟,并以磁压力为切入点研究磁场对不稳定性及射流的影响。
1 数值方法及计算模型
1.1 数值方法
在满足流体力学方程的条件下,带电荷的流体团更有利于形成团块,主要原因如下:(1)带电粒子间的碰撞频率远大于中性粒子之间的碰撞频率,因此其碰撞平均自由程较短;(2)有磁场存在时,磁场对带电粒子有侧向约束。洛伦兹力使带电粒子在垂直于磁场方向只能保持在回转半径范围内运动。等离子体通常比中性粒子有更低的密度和更高的温度,由于整个过程在短时间内完成,本文中考虑高磁雷诺数的情况,使用MHD方程来研究激波冲击R22气柱中出现的不稳定性:
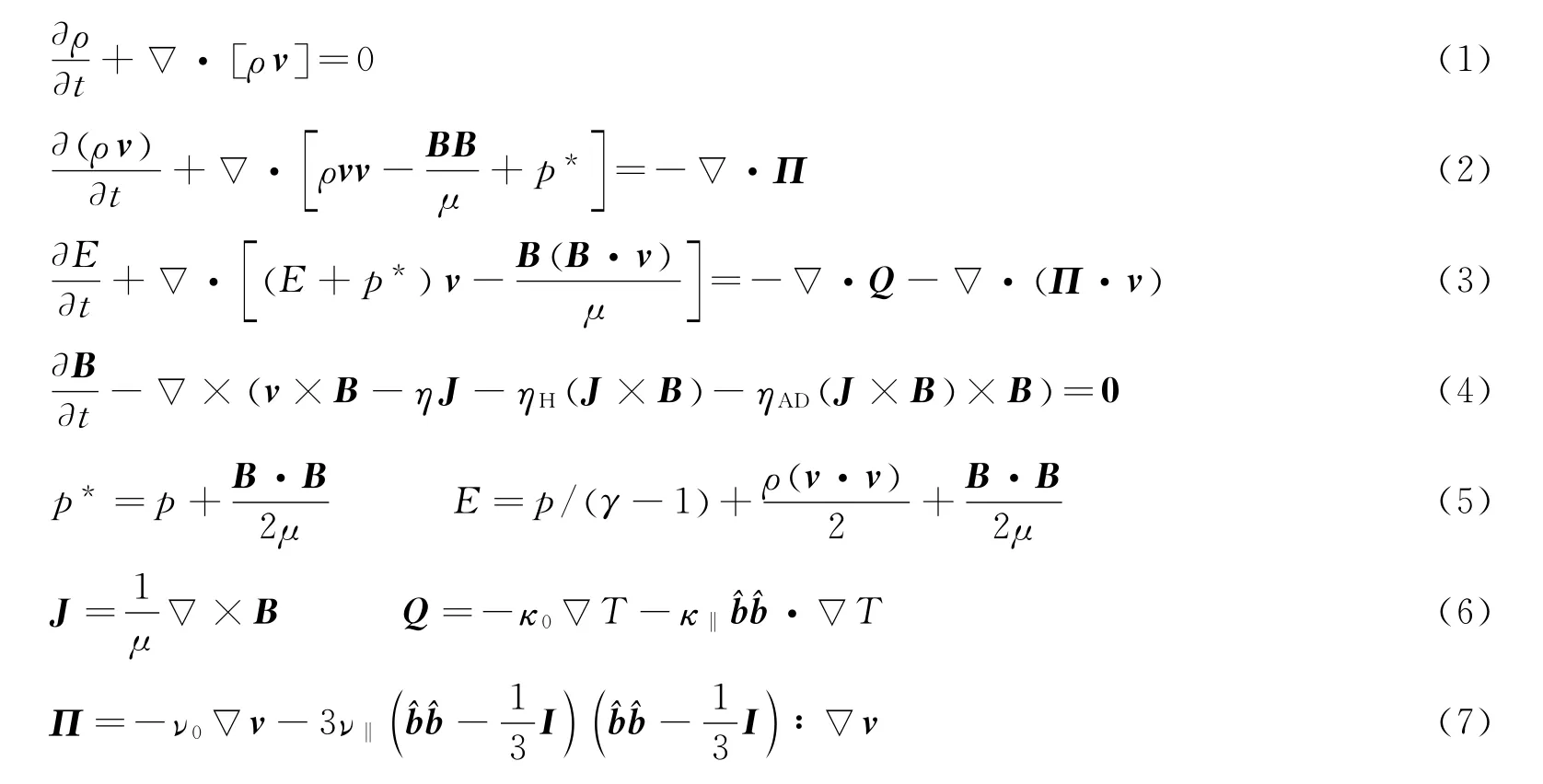
式中:ρ为质量密度,v为速度矢量,p为压力,E为能量,μ为磁导率,B为磁感应强度,^b为B的单位矢量,Π为包含各向同性与各向异性部分的黏性应力张量,分别由系数ν0和ν‖控制,γ为比热比,T为温度,I为单位张量,符号“∶”表示双点积运算。在各向异性的情况下,黏性通量限制在平行于磁场线方向。Q为热通量,同样包含各向同性与各向异性的情况,分别由系数κ0和κ‖控制。在各向异性的情况下,热通量同样限制在平行于磁场线方向。同时,感应方程包含多种非理想MHD效应,包括欧姆损耗(由电阻率η控制),霍尔效应(由系数ηH控制)和双极性扩散(由系数ηAD控制)。
本文中采用CTU+CT算法对MHD方程组进行求解,其中CTU算法是一种用于求解守恒双曲系统的不分离的二维有限体积算法,其三维变形则由J.Saltzman[19]提出。另外,由于传统的12-solve CTU算法忽略了MHD方程中始终存在的约束·B=0,不能作为求解MHD方程的有效算法,因此需要构建一个Godunov通量中网格单元边缘的平均电场算法,通常称为CT算法,该算法可以描述为以Godunov电场为预测值,以CT电场为校正值的预测过程。鉴于在文献[20]中εcCT已显示的最佳性能,本文中采用εcCT算法。该算法包含逆风偏差(根据接触模式),可以将网格对齐的平行平面流动降低到正确的Godunov电动势。
1.2 计算模型
图1为激波与R22气柱相互作用的计算模型,其中R22气泡直径为0.05m,气柱中心与左边界的距离为0.05m,与右边界的距离为0.25m,计算域高度为0.089m。初始时,气柱内采用R22作为重质气体,外部介质为空气,气体参数如表1所示。气柱内外压力均为101 325Pa,入射激波从左向右传播,来流马赫数Ma=1.22,上、下边界设为固体反射边界,而右边界设为出口条件。计算域网格采用均匀分布的笛卡尔网格,经网格收敛性测试后,区域网格总数设置为3 000×890。本文中,设初始磁场强度为0.01T(β≈2 500),令平行于来流的方向为x方向,垂直于来流的方向为y方向。

图1 计算模型Fig.1 Computational model

表1 气体参数Table 1 Gas parameters used in this paper
为了使气体受磁场影响,首先通过高温气体电离,温度为12 000K。由于含等离子体,电导率、热导率、黏性系数、霍尔系数以及双极扩散系数由以下方法确定。电导率采用基于玻尔兹曼方程得到的Spitzer公式进行计算,即由玻尔兹曼方程的碰撞积分出发,忽略短程碰撞的影响,考虑剩余的碰撞项,得到弱电场情况下由离子与电子所组成的等离子体电导率(σ)为:

式中:j=m/(2kBT),其中m为质量,kB为Boltzmann常数;γ0=0.1Z+0.49;e为电子电荷量;Z为离子电荷数。
如果碰撞积分到德拜长度为止,则库仑对数项为:

计算可得,初始电导率约为107S/m。
当气体中相当部分的原子被电离后,静电力将对粒子间碰撞起主要作用,若考虑远程作用,则离子碰撞将不能视为两体方式。通过求解玻尔兹曼方程得到一阶近似电离气体热导率为:

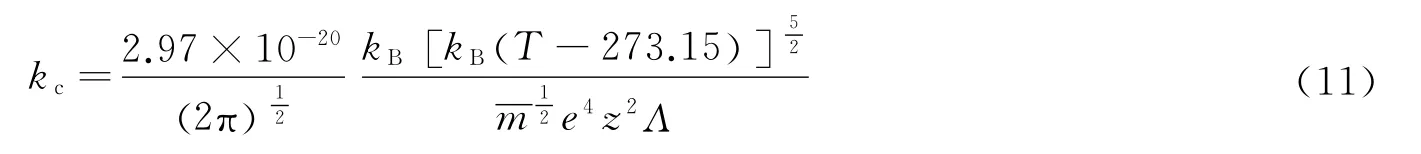
根据S.Chapman等[22]的理论可以推导出kc、ν的二阶近似值。尽管二阶近似值与一阶近似值有显著的差异,但其后各阶近似所增加的修正量都是很微小的。假定黏度均由重离子引起,电子黏度很小,由于电子的热运动速度远大于离子的热运动速度,因此热扩散效应主要是由电子引起。经过估算:本文中黏性系数约为3.72×10-5Pa·s,热导率约为1.4W/(m·K)。
由于准电中性条件,电子和离子在等离子体内不可能独立运动,当电子快速离开某等离子体单元时,单元内将形成由正电荷产生的电场,该电场阻碍电子继续离开所在体积单元,并促使离子更快地离去,这种扩散状态称为双极型状态。由于电子的扩散系数远大于离子,因此:

式中:ηi为正离子的热扩散系数,Te、Ti分别为电子、离子温度。由此可见,双极扩散系数恒小于电子自由扩散系数,而大于离子扩散系数,因此双极性电场极大影响了电子的定向速度。本文中取双极扩散系数为(10-5/ρ)m2·Pa·s-1。
Hall效应可在磁流体通道中产生横向洛伦兹力,而且体力的不均匀分布可导致二次流的产生,对流体的运动产生重要影响,因此需要考虑霍尔效应。此处,霍尔系数ηH取为10-7m3/C。
2 结果与讨论
为了验证数值方法与计算模型的可靠性,图2给出了不加磁场时入射激波与R22气柱相互作用过程计算结果与文献[21]中实验结果的对比,两者具有相同的初始条件。由图2可知:计算结果中激波的反射、绕射及发展过程均与实验结果完全相符,两者气柱的变形过程也相似;但是,由于初始时两种气体接触界面采用间断面形式,因此计算结果中接触界面上的KH不稳定性更明显,从而导致界面上、下两侧的湍流转捩过程(见图2(e))与实验结果稍有不同。
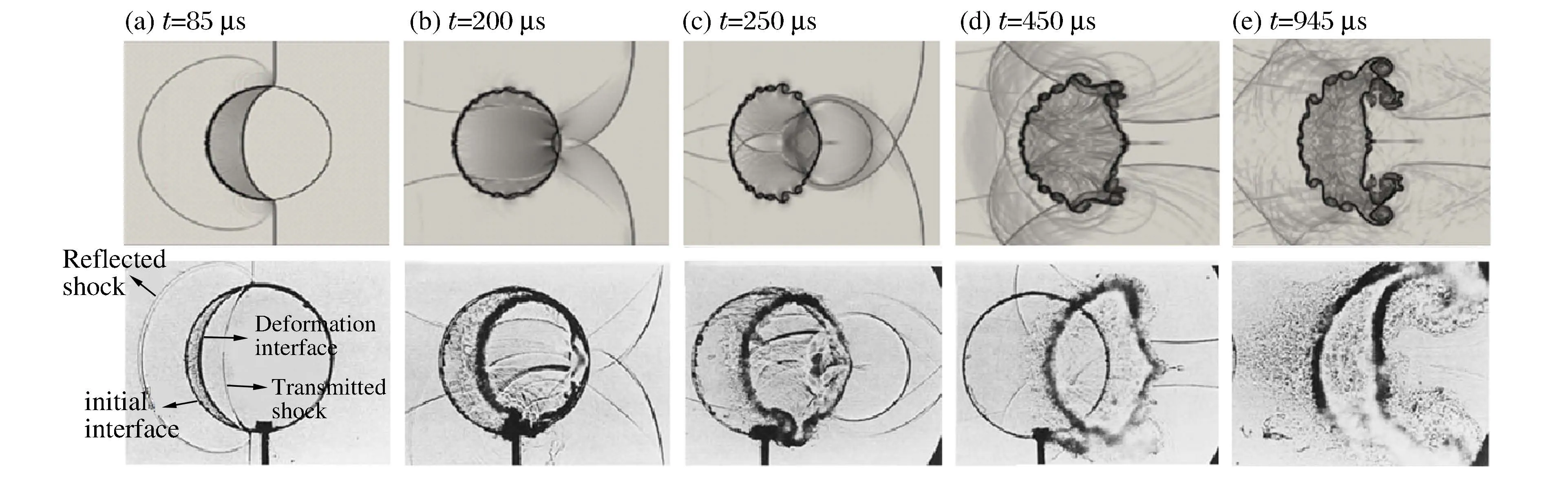
图2无磁场情况下,激波与R22气柱相互作用过程的计算纹影(上)与文献[21]实验结果(下)的对比Fig.2 Numerical results of the interaction of shock wave with the R22air column in this paper(upper row),and the experimental result in reference[21](lower row).
图3 为后期激波与R22气柱作用过程的计算纹影。从图3可以看出:由于激波对不同密度气体界面的作用,界面产生了RM不稳定性;在作用初期,随机扰动在气体界面发生,扰动振幅在界面线性增长;随着变形的加剧,振幅经历非线性增长,“气泡”与“尖钉”结构出现;随着运动的继续进行,在KH不稳定性的影响下,“尖钉”破碎,“气泡”被拉长,最终形成湍流混合状态。

图3后期激波与R22气柱作用过程计算纹影Fig.3 Numerical results of the interaction of shock wave with the R22air column in later period.
图4 为加入均匀磁场后,激波与R22气柱相互作用过程的密度纹影,其中上方子图的磁场方向垂直于来流方向(即磁场方向沿y轴正向),而下方子图中磁场方向平行于来流方向。由图4可知,与无磁场情况(见图2)相比,磁作用力能明显抑制界面处的KH不稳定性,且垂直于来流方向的磁作用力对不稳定性的控制较平行于来流方向的磁作用力更明显。为了更清晰地描述此现象,将动量方程中与磁场相关的项拆分为磁压力项(B·B)/(2μ)与磁张力项·(BB)/μ两部分,这两项均为二阶张量。然而,由于计算结果中磁压力值远大于磁张力值,下文只对磁压力的变化情况进行讨论。
由式(4)可知,垂直于速度方向的磁场分量梯度较大,磁场变化较快,该效应会引起磁场在某些位置(如垂直于磁场方向的界面处)的集中。因此,随着时间的推移,气泡界面处的磁场强度不断增大,妨碍轻质气体和重质气体的相互混合。由图4可知:当初始磁场垂直于来流方向时,磁压力作用在x轴方向,可以有效阻止气柱两侧的卷起;在t=450μs之后,由于斜压作用加剧,气柱尾部界面开处始形成涡结构;然而,沿x轴方向的磁压力抑制了不稳定性的进一步发展,最终在气柱尾部界面附近形成了上、下两个突起,如图4(f)所示。当磁场平行于来流方向时,磁压力作用在y轴方向,因上侧界面处x轴向速度的差异,在界面处卷起涡串,如图4(c)和图4(d)所示;同时,由于斜压效应,气柱上、下两侧卷起两个涡环,如图4(e)所示;随后,沿y轴方向的磁压力阻止了主涡的进一步发展,最终在主涡位置形成“尖钉”状结构,见图4(f)。由于磁化气柱的热导率远大于空气的,界面处气体混合速度较无磁场时更快。

图4 B=0.01T时不同磁场方向对激波与R22气柱作用过程的影响Fig.4 Numerical results of the interaction process of shock wave and R22air column when B=0.01T
图5和图6分别给出了磁场方向垂直或平行于来流方向时气柱对称轴上压力(p)与x方向速度(u)的分布。由图5和图6可知,与无磁场的情况[23]相比,初始压力与速度变化不大。当t=200μs时,透射激波在x轴上发生聚焦,并且在汇聚处产生局部高压区:初始磁场沿y轴正方向时,压力曲线峰值pm=700kPa,初始磁场沿x轴正方向时,pm=760kPa,均小于无磁场情况。此时,x方向速度同样处于峰值,但施加沿x轴方向磁场时的速度(u=153m/s)远大于无磁场(u=100m/s)及施加沿y轴方向磁场时的速度(u=125m/s)。随着相交点向下游移动,聚焦点的压力峰值不断下降,速度逐渐增大,并在t=250μs时达到最大值(u≈170m/s)。随后,在流体阻力作用下,速度不断衰减。综上所述,磁场的加入对压力影响不大,但却能提升透射激波聚焦时速度峰值,而磁场沿x轴方向时影响更剧烈。此外,在激波衰减过程中,沿y方向磁场较沿x方向磁场更能减缓射流的衰减。

图5 初始磁场沿y轴正方向时入射激波诱导射流产生过程Fig.5 Generation process of jet induced by incident shock wave when initial magnetic field is along yaxis

图6 初始磁场沿x轴正方向时入射激波诱导射流产生过程Fig.6 Generation process of jet induced by incident shock wave when initial magnetic field is along xaxis
图7 给出了磁场沿y轴正方向或x轴正方向时激波与R22气柱作用过程的计算纹影。由图7可知,磁场能够较好抑制RM不稳定性。当初始磁场垂直于来流方向时,界面处的横向磁压力对气体混合的抑制效果较好,同时气柱截面被压扁拉长,两个主涡在磁场作用下受到抑制,最终被拉成长条状;当初始磁场平行于来流方向时,后期气柱宽度小于磁场垂直于来流方向的情形,虽然形成两个主涡,但磁场抑制了气柱的破碎及次级涡的生成。由此可见,加入磁场后,气柱界面处没有在KH不稳定性的作用下持续失稳并卷起“珠状”次级涡,气柱顶端也未出现RM不稳定性,因此,两种方向的初始磁场对不稳定性都有较好的抑制作用。
为更清楚地看到磁场对气柱界面的影响,图8给出了初始磁场沿y轴正方向时不同时刻磁压力和磁能量的分布。由图8可知,初始时刻,透射激波在气柱内部向下游传播,圆弧反射激波向上游传播,磁压力较大处集中在气柱界面处,磁能量较大处集中在界面处及透射激波尾端。当t=165μs时,x方向磁压力沿x轴对称分布,而y方向磁压力沿x轴反对称分布;同时x方向磁压力对气体界面内侧产生向右拉力,对气体界面外侧则产生向左拉力,而y方向磁压力对气体界面内侧产生向气柱中心的拉力,而对气体界面外侧产生向外的拉力。另外,当入射激波与气柱作用时,因气柱内外气体声阻抗的不同,气柱内外会产生速度差。气柱外部界面处,空气x方向速度大于界面速度,而气柱内部界面处,空气x方向速度小于当前界面速度。由于磁场变化率与速度差密切相关,因此这两处的速度梯度会带来磁场的变化,由此产生的磁压力进一步抑制气柱界面受内外剪切力的影响(同理,对空气y方向速度,也有类似结论)。由图7(c)和图7(d)可知,发展后期,磁能量与磁压力分布类似,包裹在界面处。综上所述,当初始磁场垂直于来流方向时,磁压力始终包裹着界面,阻止界面受周围环境的进一步影响,从而防止界面上涡量的生成和扩散,抑制界面的不稳定性。

图7 后期激波与R22气柱作用过程密度纹影Fig.7 Numerical results of interaction process of shock wave with R22air column in later period
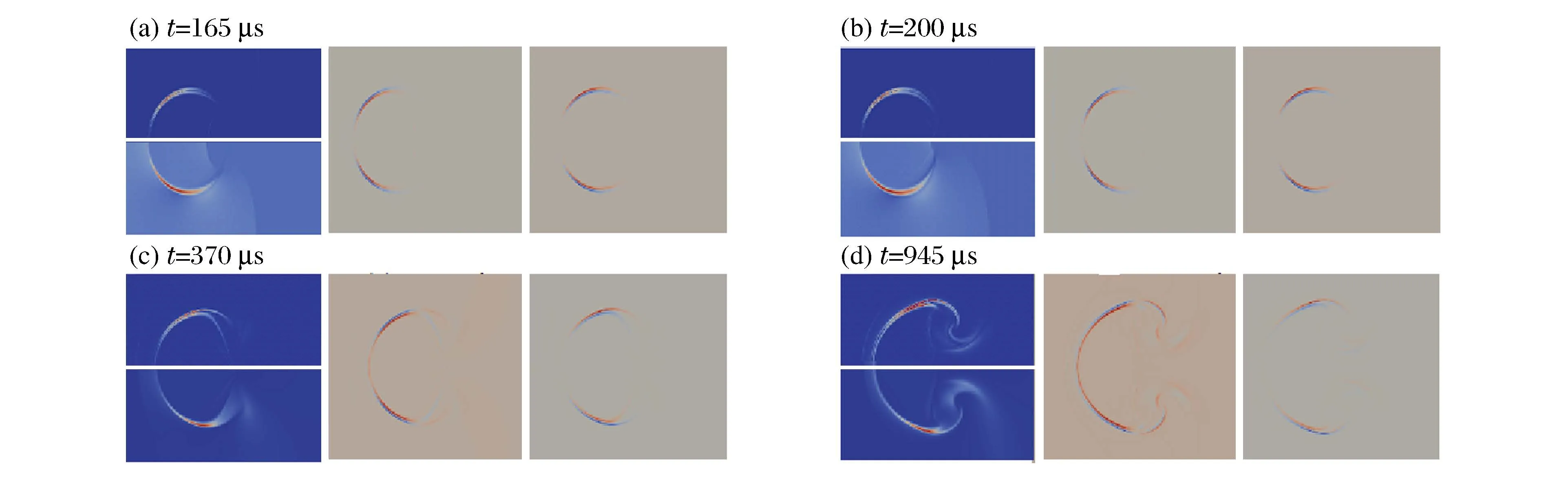
图8 初始磁场沿y轴正方向时磁压力及磁能量的分布(每幅子图中,左上为磁压力,左下为磁能量,中间和右侧分别为磁压力在x、y方向的分量)Fig.8 Magnetic pressure and magnetic energy when initial magnetic field is along yaxis(upper left:magnetic pressure;lower left:magnetic energy;middle:magnetic pressure along xaxis;right:magnetic pressure along yaxis)
图9为初始磁场沿y轴正方向时磁压力(pm)和磁能量(Em)沿横向(x方向)及纵向(y方向)的分布情况。由图9可知:当透射激波在气柱内传播时,磁能量在两个位置取值较大,一处是气柱左侧界面处,另一处位于透射激波尾部,与之前分析相符;界面处的磁压力远大于其他位置。由图9可知,气柱上、下界面处的磁压力及磁能量远大于左、右界面处。图9(c)显示:当透射及入射激波先后聚焦后,会在气柱尾端射流位置形成局部高磁压力区域,同时,该区域磁能量很低,接近于零。由于图9(c)和图9(d)中射流位置的磁压力及磁能量很低,因此磁场对射流并无明显影响;但是射流前、后的磁能量可以一定程度上抑制射流的衰减。此外,图9中不同时刻磁压力和磁能量分布曲线的形状无明显变化,但上、下界面处磁压力和磁能量的峰值随时间不断增加,这意味着界面处磁场强度随时间不断增大。
图10为初始磁场沿x轴正方向时磁压力及磁能量的分布。由图10可知,磁压力与磁能量的分布类似,其峰值均集中在界面附近。与初始磁场沿y轴正方向的情况相似,x方向磁压力沿x轴对称分布,y方向磁压力沿x轴反对称分布,同时磁压力与磁能量的作用区域更紧贴界面。由于磁压力较弱且分布不均匀,图11给出了边界处磁压力矢量分布。由图11(a)可知,当磁场平行于来流方向时,初始磁压力分布于界面处,且与剪切力及外界对其压力的合力方向相反。随后,在剪切力的作用下,气柱表面开始卷起涡,磁压力的方向随着界面变形而改变,如图11(b)所示。在主涡生成时,磁压力较大的位置依在界面附近,此对涡中心部分影响不大,如图11(c)和图11(d)所示。由此可见:当涡量大于零时(涡逆时针方向),磁压力指向涡动中心;而当涡量小于零时,磁压力指向外部。
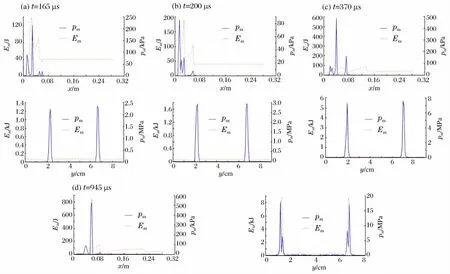
图9 初始磁场沿y轴正方向时的磁压力及磁能量分布Fig.9 Distribution of magnetic pressure and magnetic energy when initial magnetic field is along yaxis

图10 初始磁场沿x轴正方向时磁压力及磁能量分布(每幅子图中,左上为磁压力,左下为磁能量,中间和右侧分别为磁压力在x、y方向的分量)Fig.10 Magnetic pressure and magnetic energy when initial magnetic field is along xaxis(upper left:magnetic pressure;lower left:magnetic energy;middle:magnetic pressure along xaxis;right:magnetic pressure along yaxis)
图12给出了初始磁场沿x轴正方向时磁压力及磁能量沿横向及纵向的分布。由图12(a)和图12(b)可知,初始时刻,横轴和纵轴上磁压力及磁能量均小于初始磁场沿y轴正方向的情况。当t=165μs时,横轴上的磁压力集中在透射激波尾部,磁能量在顶部界面后迅速减小,接近透射激波时快速增大并达到峰值;而纵轴上磁能量和磁压力的峰值均在上、下界面处。当t=200μs时,横轴上的磁压力集中在气柱尾端,磁能量仍然在透射激波尾部,纵轴上的磁压力不断增大;此时由于涡在界面处开始生成,纵轴上磁压力的分布不对称。当t=370μs时,透射激波聚集,在尾部形成射流,圆弧形二次激波向外传播,并最终碰到上、下界面发生反射;此时,横轴上磁压力与磁能量最大值位置相同,均在气柱尾部界面处达到峰值,而纵轴上的磁压力峰值则继续增大,如图12(c)所示。当两个主涡形成后,纵轴处主涡位置的磁能量较为明显,但此时磁能量及磁压力最大位置仍在界面附近;横轴上磁压力峰值减小,磁能量继续增加,并集中在气柱尾部,如图12(d)所示。

图11 初始磁场沿x轴正方向时边界处磁压力矢量图Fig.11 Vector diagram of magnetic pressure on the interface when initial magnetic field is along xaxis
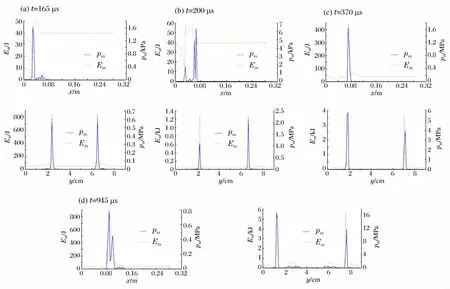
图12 初始磁场为x轴正方向时磁压力及磁能量分布Fig.12 Distribution of magnetic pressure and magnetic energy when initial magnetic field is along xaxis
3 结 论
基于CTU+CT算法,对磁场环境下激波冲击重质气体进行数值模拟,并与不加磁场的情况进行对比,所得结论如下。
(1)R22气柱与入射激波作用后,由于KH不稳定性,气柱上、下两侧不断卷起最终形成两个主涡。同时,由于RM不稳定性,后期气柱左端界面处产生了“尖钉”与“气泡”状结构。磁场能够抑制界面不稳定性,平行磁场通过减少界面上涡量的生成减缓不稳定性的增长;垂直磁场则通过包裹界面的磁力线压缩界面,抑制剪切力对界面的作用,使界面处不再卷起,从而抑制界面不稳定性。
(2)垂直磁场和平行磁场都可以很好地抑制RM不稳定性,对于KH不稳定性,垂直磁场的控制效果更好,不仅可以抑制界面上涡串的卷起,还可以阻止主涡的发展,而平行磁场做不到后者。磁场对射流影响不大,射流处的磁能量可以在一定程度上抑制射流的衰减,同时,垂直磁场可以减小射流聚焦时压力及速度峰值。
(3)当磁场强度较小(β≈2 500)时,初始磁场对激波与R22气柱作用过程没有显著影响,随后磁压力及磁能量不断增加,从而抑制不稳定性的发展。磁压力及磁能量对界面影响很大,在上、下界面处达到峰值。同时,磁压力对界面没有压缩作用,而是产生一个反向作用力减小外界对界面的影响。当涡形成后,磁场对涡量影响不大,但可以通过抑制外界的剪切力阻止其进一步的发展。
[1] Meyer K A,Blewett P J.Numerical investigation of the stability of a shock-accelerated interface between two fluids[J].Physics of Fluids,1972,15(5):753-759.
[2] Zhang Q,Sohn S I.An analytical nonlinear theory of Richtmyer-Meshkov instability[J].Physics Letters A,1996,212(3):149-155.
[3] Anuchina N N,Volkov V I,Gordeychuk V A,et al.Numerical simulations of Rayleigh-Taylor and Richtmyer-Meshkov instability using MAH-3code[J].Journal of Computational and Applied Mathematics,2004,168(1/2):11-20.
[4] Ruev G A,Fedorov A V,Fomin V M.Development of the Richtmyer-Meshkov instability upon interaction of a diffusion mixing layer of two gases with shock waves[J].Journal of Applied Mechanics and Technical Physics,2005,46(3):307-314.
[5] Niederhaus J H J,Greenough J A,Oakley J G,et al.A computational parameter study for the three-dimensional shock-bubble interaction[J].Journal of Fluid Mechanics,2008,594:85-124.
[6] Thornber B,Drikakis D,Youngs D.Large-eddy simulation of multi-component compressible turbulent flows using high resolution methods[J].Computers and Fluids,2008,37(7):867-876.
[7] Hejazialhosseini B,Rossinelli D,Bergdorf M,et al.High order finite volume methods on wavelet-adapted grids with local time-stepping on multicore architectures for the simulation of shock-bubble interactions.[J].Journal of Computational Physics,2010,229(22):8364-8383.
[8] Schilling O,Latini M.High-order weno simulations of three-dimensional reshocked Richtmyer-Meshkov instability to late times:Dynamics,dependence on initial conditions,and comparisons to experimental data[J].Acta Mathematica Scientia,2010,30(2):595-620.
[9] Tian B,Shen W,Jiang S,et al.A global arbitrary Lagrangian-Eulerian method for stratified Richtmyer-Meshkov instability[J].Computers and Fluids,2011,46(1):113-121.
[10] Shankar S K,Kawai S,Lele S K.Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder[J].Physics of Fluids,2011,23(2):131.
[11] Bailie C,Mcfarland J A,Greenough J A,et al.Effect of incident shock wave strength on the decay of Richtmyer-Meshkov instability-introduced perturbations in the refracted shock wave[J].Shock Waves,2012,22(6):511-519.
[12] Chandrasekhar S.Hydrodynamic and hydromagnetic stability[M].Dover Publications,1961.
[13] Wheatley V,Pullin D I,Samtaney R.Stability of an impulsively accelerated density interface in magnetohydrodynamics[J].Physical Review Letters,2005,95(12):125002.
[14] Wheatley V,Samtaney R,Pullin D I.The magnetohydrodynamic Richtmyer-Meshkov instability:The transverse field case[C]∥18th Australasian Fluid Mechanics Conference.Australasian Fluid Mechanics Society,2012.
[15] Khan M,Mandal L,Banerjee R,et al.Development of Richtmyer-Meshkov and Rayleigh-Taylor instability in presence of magnetic field[J].Nuclear Instruments &Methods in Physics Research A,2011,653(1):2-6.
[16] Cao J,Wu Z,Ren H,et al.Effects of shear flow and transverse magnetic field on Richtmyer-Meshkov instability[J].Physics of Plasmas,2008,15(4):445-514.
[17] Shin M S,Stone J M,Snyder G F.The magnetohydrodynamics of shock-cloud interaction in three dimensions[J].Astrophysical Journal,2008,680(1):336-348.
[18] 李源,罗喜胜.黏性、表面张力和磁场对Rayleigh-Taylor不稳定性气泡演化影响的理论分析[J].物理学报,2014,2(8):277-285.Li Yuan,Luo Xisheng.Theoretical analysis of effects of viscosity,surface tension,and magnetic field on the bubble evolution of Rayleigh-Taylor instability[J].Acta Physica Sinica,2014,2(8):277-285.
[19] Saltzman J.An unsplit 3Dupwind method for hyperbolic conservation laws[J].Journal of Computational Physics,1994,115(1):153-168.
[20] Gardiner T A,Stone J M.An unsplit Godunov method for ideal MHD via constrained transport[J].Journal of Computational Physics,2005,205(2):509-539.
[21] Haas J,Sturtevant B.Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J].Journal of Fluid Mechanics,1987,181(1):41-76.
[22] Chapman S,Cowling T G.The mathematical theory of non-uniform gases[M].London:Cambridge University Press,1970.
[23] 沙莎,陈志华,薛大文.激波冲击R22重气柱所导致的射流与混合研究[J].物理学报,2013,62(14):144701.Sha Sha,Chen Zhihua,Xue Dawen.The generation of jet and mixing induced by the interaction of shock wave with R22cylinder[J].Acta Physica Sinica,2013,62(14):144701.
Influence of magnetic field on interaction of shock wave
with R22heavy gas column
Lin Zhenya,Zhang Huanhao,Chen Zhihua,Liu Ying
(National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing210094,Jiangsu,China)
To study the interaction process of the plane incident shock wave with the magnetized R22 heavy gas column,we numerically simulated the deformation process of the shock-wave-induced R22 heavy gas column resulting from Kelvin-Helmholtz(KH)and Richtmyer-Meshkov(RM)instabilities under different initial conditions,and analyzed the jet focusing and inducing process by the transmitted shock wave.When the magnetic field was taken into consideration,the CTU+CT algorithm satisfying the divergence equation of the magnetic field at any time was adopted in the numerical simulation.The results show that the magnetic field is capable of restraining the instability of the shockwave-induced R22gas column.Both the normal magnetic field(vertical to the flow direction)and the tangential magnetic field(parallel to the flow direction)can inhibit the RM instability.However,the restraining of the normal magnetic field is more effective than that of the tangential one with regard to the KH instability,as it can not only inhibit the vortex train rolling up on the interface but also prevent the bound vortex from developing.Besides,it is found that the magnetic field has little influence on the jet,and the magnetic energy at the jet point can suppress the jet attenuation to some extent while the normal magnetic field can reduce the peak pressure and velocity when the transmitted shock wave is focused.
magnetization gas;magneto-hydro-dynamics;magnetic field;instability;shock wave
O354.5国标学科代码:1303520
A
10.11883/1001-1455(2017)04-0748-11
(责任编辑 王玉锋)
2016-03-24;
2016-08-23
国家自然科学基金项目(11272156);中国博士后科学基金项目(2015M571757)
林震亚(1990- ),男,博士;通信作者:张焕好,122488989@qq.com。

