脆性材料中应力波衰减规律与层裂实验设计的数值模拟＊

巫绪涛，廖 礼

（合肥工业大学土木与水利工程学院，安徽合肥230009）

脆性材料中应力波衰减规律与层裂实验设计的数值模拟＊

巫绪涛，廖 礼

（合肥工业大学土木与水利工程学院，安徽合肥230009）

对混凝土、岩石类脆性材料的层裂实验进行了有限元模拟，研究了应力波在此类材料中传播的衰减规律，包括两类机制：弹性波因大尺寸试样的几何弥散产生的小幅度线性衰减、与应变率相关的黏塑性波因本构关系导致的指数衰减。在此基础上，提出了包含常数项的指数型应力波峰值拟合公式。建议采用可以忽略应力波衰减影响的细长形试样进行层裂实验。混凝土类脆性材料层裂破坏模拟结果显示，有限元模拟得到的层裂片厚度与一维应力波理论得到的结果非常吻合，验证了按一维应力波理论确定层裂强度的实验方法的有效性。通过对比3种不同入射波形下层裂片的形状和净拉应力波形，发现不对称的入射波形状更有利于实验获得平直的层裂断面和较准确的层裂强度。

脆性材料；应力波；衰减规律；层裂

层裂是指当压力脉冲在杆或板的自由面反射形成拉伸脉冲时，在邻近表面的某处形成相当高的拉应力，一旦满足某动态断裂准则，则该处材料发生破裂的现象［1］。由于混凝土、岩石类脆性材料存在典型的拉压不对称性，在冲击载荷作用下此类材料中经常存在层裂这种失效方式。与单纯的拉伸失效不同，材料在层裂失效前往往受到较强的冲击压应力作用而损伤，因此层裂失效与应变率、压缩损伤及拉伸损伤具有复合关系。

1914年，Hopkinson在硝化棉炸药爆炸冲击软钢板的实验模型中首次发现了层裂这一现象。J．S．Rinehart［2］在Hopkinson研究的基础之上，对钢、黄铜等材料的层裂现象进行了详细分析，提出了层裂破坏的瞬时破坏准则，为层裂实验研究奠定了重要基础。2001年J．R．Klepaczko等［3］用分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）装置对混凝土进行了层裂实验，并提出了基于一维应力波理论的混凝土层裂强度的测量方法，但是该方法未考虑应力波在混凝土试样中的弥散和衰减。F．G．Díaz－Rubio等［4］用相同的方法研究了陶瓷材料的层裂，通过在试样上粘贴应变片直接测量了应力波，他们提出应力波在陶瓷试样中的传播不发生衰减，且认为层裂之前材料经受的冲击压缩对其力学性能不产生影响。胡时胜等［5］、J．Zhu等［6］分别对混凝土及复合软纤维增韧砂浆进行了层裂实验研究，根据应变片测量数据，结合黏弹性理论，提出了混凝土中应力波传播的纯指数型衰减规律。Z．Rong等［7］、陈柏生等［8］分别对超高强度混凝土和钢纤维混凝土进行了层裂实验，均采用应变片测量试样中应力波的传播规律，但从实验数据上看，应力波在试样中传播的弥散和衰减很小。上述实验所反映的应力波衰减规律的区别，往往归结于混凝土材质的不均匀性，未得到很好的解释与研究。因此对于混凝土、岩石等脆性材料的层裂实验是否需要考虑应力波衰减存在争议。

在本文中采用有限元软件ANSYS／LS－DYNA，对基于SHPB装置的层裂实验进行数值模拟，结合实验分析应力波在混凝土、岩石类脆性材料中传播的衰减规律，并验证按一维应力波理论确定层裂强度的实验方法的有效性。

1 层裂实验原理及有限元模型

1．1 层裂实验原理

层裂实验采用Hopkinson杆作为加载工具，长试样直接紧贴入射杆，用长度为50～100mm的撞击杆产生短历时入射波。在入射杆和试样端面粘贴应变片，其中：在入射杆同一截面相隔180°粘贴两个轴向应变片，以消除弯曲效应的影响；沿试样长度方向每隔100mm选择5～7个截面粘贴轴向应变片，每个截面均布2～3片，以减小试样非均质的影响。

实验过程中，通过高压气体驱动撞击杆，产生入射应力波。入射波到达压杆与试样的交界面处，一部分脉冲反射，另一部分透过试样向前传播。压杆中的入射波和反射波由粘贴在入射杆上的应变片采集，将二者在试样与压杆接触面叠加，以获得输入试样的透射波；试样中传播的透射波由粘贴在试样上的应变片采集。试样中的压缩波传播到自由面时将反射为拉伸波，两者叠加的净拉应力达到试样的层裂强度时，试样发生层裂破坏。图1为层裂实验装置简图，图2为某花岗岩试样层裂实验装置及试样发生层裂破坏的照片。

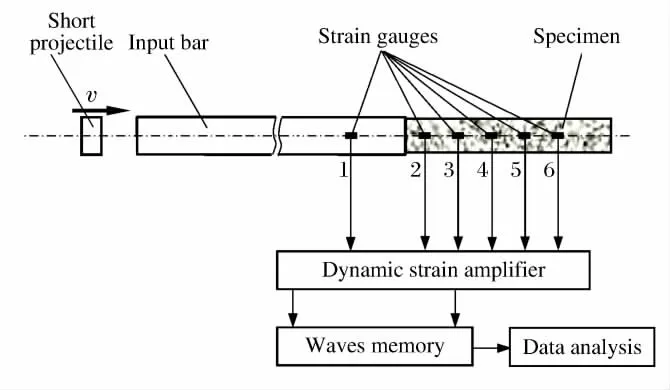
图1层裂实验装置简图Fig．1 Scheme of spalling experiment

图3 所示为试样中的透射应力波（σ），其中曲线1是由粘贴在入射杆上的应变片采集的入射波和反射波叠加而成，曲线2～曲线6是由粘贴在试样上的应变片采集的透射应变波乘以材料弹性模量得到。可见，各处波形基本相似，但其峰值随传播距离的增加有衰减现象，衰减幅度随传播距离的增大而减小。据此拟合透射波峰值随传播距离的衰减规律，代入一维应力波传播程序，得到试样中净拉伸波的产生过程，见图4，其中l表示到试样自由面的距离。可见，距自由面150mm处出现净拉应力，其峰值由小逐渐变大。由实测的层裂片厚度（见图2（b））和图4中拉应力峰值包络线的交点，可以确定试样的层裂强度。

图2 花岗岩试样层裂实验Fig．2 Spalling experiment of granite specimen

图3 试样中的透射波Fig．3 Transmission wave of specimen

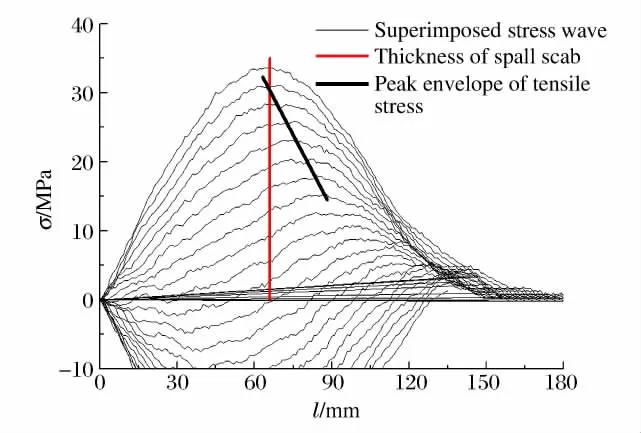
图4 层裂强度处理方法示意Fig．4 Spalling strength processing method

1．2 有限元模型

按图1建立层裂实验的有限元模型，其中压杆长3 000mm，试样有两种长度，分别为2 000mm和600mm，试样和压杆的直径均为100mm。

对于压杆，采用线弹性模型：弹性模量E＝200GPa，密度ρ＝7 850kg／m3，泊松比ν＝0．3。对于试样，采用两种本构模型：（1）线弹性本构模型，弹性模量E＝30GPa，密度ρ＝2 400kg／m3，泊松比ν＝0．2；（2）HJC（Holmquist－Johnson－Cook）模型，采用T．J．Holmquist等［9］对静态抗压强度为48MPa的混凝土提出的原始参数，如表1所列，包括基本力学参数（切变模量G、静态单轴抗压强度f′c、拉伸强度T）、特征化极限面参数（黏聚强度参数A、压力硬化系数B、压力硬化指数N、最大等效应力Smax）、损伤参数（损伤常数D1和D2、材料断裂的最小塑性应变εf，min）、状态方程参数（弹性极限对应的静水压力pc和体积应变μc，压实时的静水压力pl和体积应变μl，压力常数k1、k2和k3）、率效应参数（应变率效应系数C、参考应变率ε0）。

表1 HJC模型参数Table 1 Parameters of HJC constitutive model

HJC模型是一种弹黏塑性本构模型，考虑了材料损伤、应变率效应和静水压力对屈服面的影响。本构关系采用三段式状态方程描述，等效强度的应变率效应和损伤累积破坏准则类似于Johnson－Cook模型。由于它能较好地描述混凝土和岩石类脆性材料在高速撞击和侵彻下所产生的损伤、破碎及断裂（或层裂）等行为，因此在数值模拟中得到了广泛的应用。考虑到该模型无拉伸失效模式，为此我们通过增加侵蚀失效准则来控制单元的破坏。

为简化模型，在入射杆左端面加载不同峰值、不同上升／下降沿的短历时三角形速度波作为加载载荷，所有单元类型均采用实体结构单元Solid164，由此建立有限元模型，并进行网格划分。为减小网格依赖性影响，经过大量试算，取计算稳定时的单元大小和密度作为正式模拟时的网格。

2 应力波在试样中的衰减规律

对应力波在试样中传播的衰减规律进行有限元模拟研究，入射杆左端面加载上升沿和下降沿均为10μs的对称三角形应力波，试样不增加侵彻失效准则。当输入试样的应力波强度小于屈服应力时，混凝土、岩石类材料的黏性行为可以忽略不计，视作线弹性材料。因此，首先采用线弹性本构关系对试样进行模拟，得到透射波峰值随传播距离的变化规律，如图5（a）所示。可以发现，应力波峰值σp随传播距离l的增加呈线性衰减规律：

式中：σ0为试样－压杆接触面的应力峰值；k为线性衰减速率，k随σ0线性增加，如图5（b）所示。这种情况产生的应力波衰减与材料的本构关系无关，完全是由于在大直径试样中传播的应力波脉冲宽度较短，非一维应力状态引起的几何弥散所致，总体来说衰减幅度较低。

当输入试样的应力波强度超过屈服应力时，与应变率相关的微裂纹和微孔洞损伤导致材料的黏性机制加剧。此时采用HJC模型对试样进行模拟，在此模拟了初始强度为130MPa和95MPa的透射波（对应的峰值分别为σp1、σp2）的衰减规律，如图6所示。可见，初期应力波峰值的衰减幅度很大，但传播一定距离后趋于平稳，与图3反映的规律一致。其衰减规律可以用下式拟合：

式中：α是与材料参数及应力波强度有关的衰减系数，其值越小，应力波峰值衰减得越剧烈；σ1、σ2为拟合参数，分别代表不衰减的弹性波分量和指数衰减的黏塑性波分量。

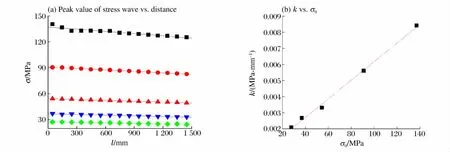
图5 短历时应力波在线弹性材料中的衰减规律Fig．5 Attenuation of short duration stress wave in linear elastic material

一些文献［56］提出，混凝土、岩石类脆性材料具有典型的黏弹性特点，得到应力波传播的纯指数型衰减规律：

按照式（3），应力波衰减迅速，无法描述图6透射波峰值的衰减规律。

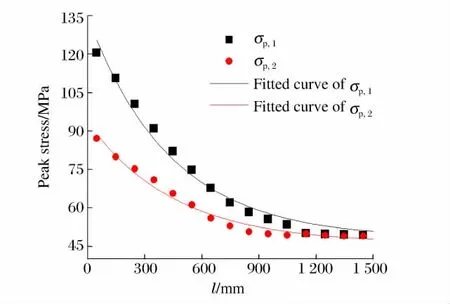
图6 短历时应力波在HJC模型材料中的衰减规律Fig．6 Attenuation of short duration stress wave in HJC material

式（2）的物理意义在于将脆性材料的黏性机制分为两个不同阶段：（1）当应力较小时，其内部的微裂纹、微孔洞等损伤行为较弱，材料具有弱黏性效应；（2）当应力增大后，损伤导致的黏性效应加剧。显然，当传入试样的脉冲强度越低或材料的屈服应力越高，应力波传播的衰减越小，这就是不同研究者所获实验数据［58］存在差别的原因。式（2）将脆性材料中传播的应力波分成两部分：一部分为忽略黏性行为、仅存在几何弥散的弹性波，其峰值为σ1，由于其衰减幅度很小，可以简化为常数项，根据表1中HJC模型的屈服应力，得到σ1＝48MPa；另一部分是与材料本构关系相关的呈指数衰减的黏塑性波，其初始强度σ2与σ1之和即为传入试样的应力波峰值σp。由式（2）得到的拟合效果见图6，两条拟合曲线的非线性相关系数r2均超过0．99。对于初始强度为130和95MPa的透射波，其衰减系数α的拟合值分别为0．002 2和0．002 5mm－1，高速冲击下衰减系数降低，反映了黏性效应的增强。

图7所示为两种不同冲击载荷下某同类混凝土试样层裂实验中应变片测得的应力波峰值（σp1、σp2）变化以及按式（2）拟合得到的结果。通过拟合得到：低速冲击下，σ1＝16．0MPa，σ2＝10．8MPa，α＝0．004 9mm－1；高速冲击下，σ1＝14．3MPa，σ2＝40．7MPa，α＝0．003 1mm－1。低速和高速冲击载荷下，混凝土试样的σ1较接近，并且高速冲击下衰减系数α较小，与图6所得结果相符合。

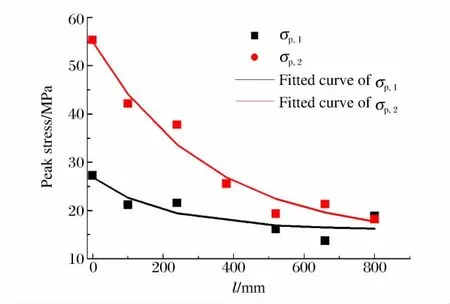
图7 应力波在细长混凝土试样中的衰减规律Fig．7 Attenuation of stress wave in slender concrete specimen

综上所述，应力波在混凝土等脆性材料试样中的传播存在衰减现象，并且与传入试样的初始脉冲强度密切相关。由于弹性波的衰减幅度很小，黏塑性波衰减迅速，因此当采用细长试样（长径比≥15），或传入试样的初始脉冲强度小于材料屈服应力（损伤软化）时，在层裂实验过程中可以不考虑应力波的衰减，直接在试样距自由端1／3位置处粘贴应变片，测量试样中的透射波。

3 层裂模拟实验分析

试样采用HJC模型，并增加最大拉应力瞬时断裂准则，设定混凝土试样的层裂强度为20MPa，对其层裂进行模拟。考虑了3种情况：（1）试样长度为2 000mm，压杆端面载荷为上升沿和下降沿均为10μs的对称三角波，传入试样的脉冲幅度为90MPa；（2）试样长度为2 000mm，压杆端面载荷的上升沿为4μs，下降沿为16μs，传入试样的脉冲幅度为90MPa；（3）试样长度为600mm，压杆端面载荷的上升沿为16μs，下降沿为4μs，传入试样的脉冲幅度为90MPa。图8为模拟得到的发生层裂瞬间混凝土的破坏情况。根据一维应力波理论，得到净拉应力变化规律，如图9所示。

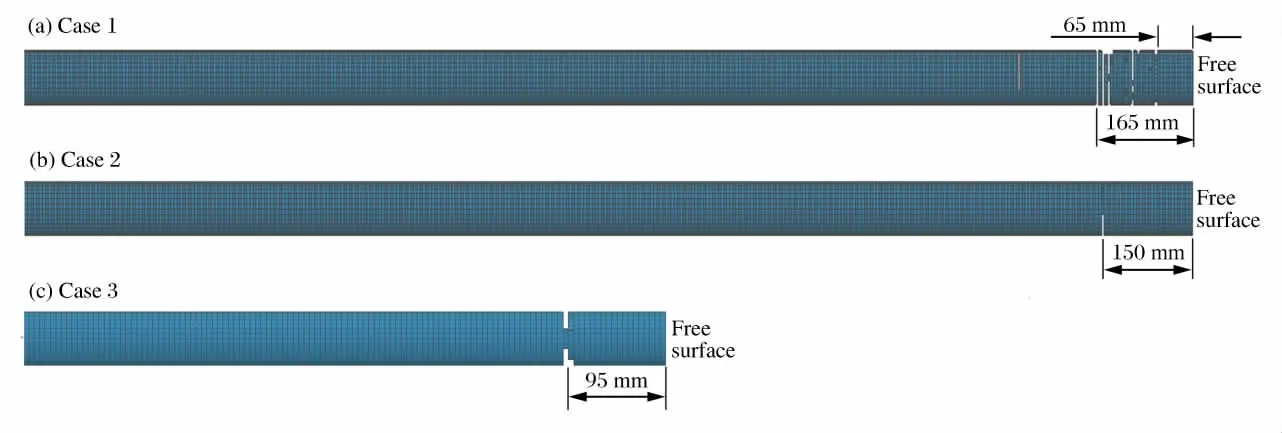
图8 采用有限元方法得到的层裂片厚度Fig．8 Scab thicknesses obtained by finite element method

图9 由一维应力波理论得到的层裂片厚度Fig．9 Scab thickness by one－dimensional stress wave theory

对于第1种情况：层裂破坏同时发生在距试样自由端65～165mm之间，如图8（a）所示；其净拉应力变化曲线（见图9（a））呈现多峰的平台波动，其最远和最近峰值对应的层裂片厚度分别为68和161mm，与数值模拟结果吻合。这种情况在实际层裂实验中表现为层裂面严重倾斜或小碎段多，如图10所示，不利于获得准确的层裂强度。

对于第2种情况：层裂破坏发生在距试样自由端150mm处，如图8（b）所示；其净拉应力曲线（见图9（b））只有一个峰值，且单调线性增长，由20MPa层裂强度和净拉应力峰值可确定层裂片厚度，为146mm，与数值模拟结果非常接近。这种情况在实验中表现为层裂面较平直，类似于图2所示情况，有利于实验中获得较准确的层裂强度。

图10 层裂实验中的不规则断面Fig．10 Irregular cross－section in spalling experiment

对于第3种情况：层裂破坏发生在距试样自由端95mm处，如图8（c）所示。由于试样长度较短，因此用一维应力理论获得净拉应力的变化规律时，按式（2）考虑了应力波的衰减，同时假设拉伸波的衰减规律与压缩波一致，最终确定的层裂片厚度为97mm，与数值模拟结果很接近。从图9所示的净拉应力变化趋势上看，第2种和第3种情况中拉应力峰值的单调性较为理想。

4 结 论

利用有限元方法对应力波在脆性材料中的传播规律和层裂实验进行了模拟研究，得到以下主要结论：

（1）实验和数值模拟均证实应力波在混凝土和岩石等脆性材料中的传播具有衰减现象，并可分为两部分，低于屈服应力的弹性波仅产生由于几何弥散导致的线性衰减，衰减幅度较小，而超过屈服应力的黏塑性波呈指数衰减；

（2）可以采用长径比为15左右的细长试样进行层裂实验，实验过程中可以不考虑应力波的衰减，直接在试样距自由端1／3位置处粘贴应变片，测量试样中的透射波；

（3）层裂实验中应采用波形整形技术产生上升沿和下降沿不对称的入射脉冲，此时净拉应力波形的峰值单一，更有利于获得较准确的层裂强度。

［1］ 王礼立．应力波基础［M］．第2版．北京：国防工业出版社，2005．

［2］ Rinehart J S．Some quantitative data bearing on the scabbing of metals under explosive attack［J］．Journal of Applied Physics，1951，22（5）：555－560．

［3］ Klepaczko J R，Brara A．An experimental method for dynamic tensile testing of concrete by spalling［J］．International Journal of Impact Engineering，2001，25（4）：387－409．

［4］ Díaz－Rubio F G，Pérez J R，G lvez V S．The spalling of long bars as a reliable method of measuring the dynamic tensile strength of ceramics［J］．International Journal of Impact Engineering，2002，27（2）：161－177．

［5］ 胡时胜，张磊，武海军，等．混凝土材料层裂强度的实验研究［J］．工程力学，2004，21（4）：128－132．Hu Shisheng，Zhang Lei，Wu Haijun，et al．Experimental study on spalling strength of concrete［J］．Engineering Mechanics，2004，21（4）：128－132．

［6］ Zhu J，Sun C，Qian Z，et al．The spalling strength of ultra－fiber reinforced cement mortar［J］．Engineering Failure Analysis，2011，18（7）：1808－1817．

［7］ Rong Z，Sun W．Experimental and numerical investigation on the dynamic tensile behavior of ultra－high performance cement based composites［J］．Construction ＆Building Materials，2012，31（6）：168－173．

［8］ 陈柏生，肖岩，黄政宇，等．钢纤维活性粉末混凝土动态层裂强度试验研究［J］．湖南大学学报（自然科学版），2009，36（7）：12－16．Chen Baisheng，Xiao Yan，Huang Zhengyu，et al．Experimental study on the spalling strength of fiber reactive powder concrete［J］．Journal of Hunan University（Natural Sciences），2009，36（7）：12－16．

［9］ Holmquist T J，Johnson G R，Cook W H．A computational constitutive model for concrete subjected to large strains high strain rates，and high pressure［C］∥Jackson N，Dickert S．The 14th International Symposium on Ballistics．USA：American Defense Prepareness Association，1993：591－600．

Numerical simulation of stress wave attenuation in brittle material and spalling experiment design

Wu Xutao，Liao Li

（School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei 230009，Anhui，China）

Using finite element simulation，we investigated the spalling of such brittle materials as concrete and rock，studied the attenuation mechanism governing the stress wave propagation through the specimen of brittle materials，and found two kinds of mechanisms：the small amplitude linear attenuation of the elastic wave due to the geometric dispersion of the large size specimen，and the exponential decay of the viscoplastic wave associated with the strain rate due to the constitutive relation．Based on this，we proposed a peak fitting formula of exponential type stress wave with a constant term．It is suggested that we should choose a slender specimen in the spalling test in which the attenuation of the stress wave can be ignored．In addition，we studied the spalling damage of concrete and rock．The scab thickness obtained from the finite element method agrees well with one－dimensional stress wave theory，verifying that the method for determining the spalling strength by onedimensional stress wave theory is effective．By comparing the scab shape and the tensile stress wave of the brittle material loading by three kinds of the incident wave，we proved that it is more feasible to obtain a flatter spalling cross－section and more precise strength by using an asymmetric incident wave．

brittle material；stress wave；attenuation law；spalling

O346．1国标学科代码：1301545

A

10．11883／1001－1455（2017）04－0705－07

（责任编辑 王 影）

2015－12－23；

2016－03－23

巫绪涛（1971－ ），男，博士，副教授，wuxvtao＠sina．com。