平面体系机动分析模式及其应用
王建祥+胡景龙+陈国新
摘要:平面体系的机动分析是结构力学课程教学中的重点和难点之一,是学习结构力学后续内容的基础和前提。针对机动分析时学生遇到的实际问题,经过对大量习题的分析、归纳和总结,提出平面体系“2+2+3+4”机动分析模式,使平面体系机动分析过程可以按照一定的模式和步骤进行,让看似无从下手的分析变得有章可循。针对三种不同机动分析方法,分别辅以例题对分析步骤进行详细说明,为结构力学平面体系机动分析教学提供新的模式和参考。
关键词:结构力学;平面体系;自由度;机动分析模式
中图分类号:G642.0;TU311 文献标志码:A 文章编号:1005-2909(2017)03-0062-04
平面体系的机动分析主要是确定结构体系的几何组成性质,判断体系是否几何不变及其约束情况。体系只有在几何不变的情况下,才能作为结构使用 [1]。平面体系的机动分析是结构力学课程后续计算结构内力的基础和前提,也是学习结构力学课程的重点和难点之一。判断几何不变体系只有两刚片规则和三刚片规则,这两个规则比较容易理解。但是,平面体系千变万化,机动分析中概念多,技巧性强[2-3],对于刚接触结构力学课程学习的学生来说,往往觉得规则简单,但分析时却又感到无从下手。本文针对平面体系机动分析的特点,以及学生解题遇到的困难,经过分析、归纳和总结,提出平面体系“2+2+3+4”机动分析模式,使平面体系机动分析过程可以按照一定的模式和步骤进行,使看似无从下手的机动分析能够有章可循。
一、 “2+2+3+4”机动分析模式
“2+2+3+4”机动分析模式,包括:两个机动分析判断准则、两种体系类型、三种机动分析方法、四种结构简化方法。“2+2+3+4”机动分析模式将平面结构体系的简化、机动分析和判断准则结合起来,相互联系,前后呼应,共同组成了平面体系的机动分析模式。
(一)两个机动分析判断准则
1.两刚片规则
两个刚片用一个铰和一根不通过此铰的链杆连接,为几何不变体系,且无多余约束;若链杆延长线通过此铰,组成的体系则是瞬变体系。
2.三刚片规则
三个刚片用三个不共线的铰两两相连,为几何不变体系,且无多余约束;若三个单铰在同一直线上, 组成的体系则为瞬变体系。
两个判断规则中连接的铰,可以是实铰,也可以为虚铰。[4-5]
(二)两种体系类型
根据体系与基础连接链杆的个数,把体系分析为两种类型。
第一种体系类型:体系与基础连接大于三根链杆(r>3);第二种体系类型:体系与基础连接等于三根链杆(r=3)。如果体系与基础连接小于三根链杆(r<3),则该体系为几何常变体系,无需机动分析。
(三) 三种机动分析方法
针对平面体系两种类型,主要有三种机动分析方法。
对于第一种体系类型,即体系与基础连接大于三根链杆(r>3),机动分析时,首先把基础作为一个基本刚片,然后根据具体情况,又分为两种分析方法。一是该结构体系局部可以和基础构成几何不变体系,基本刚片可以扩大至局部几何不变部分,然后依次将基本刚片由小到大、由下到上、由里向外一层层进行分析,可以通过扩大基本刚片到整体。二是该结构体系局部不能和基础构成几何不变体系,或者可以构成几何不变,但不能通过扩大刚片至整体。这种情况为,基本刚片如果能扩大应先扩大基本刚片,然后简化其余结构为最多两个刚片(或一个刚片),加上基础刚片,应用三刚片规则(或两刚片规则)进行分析判断。这种情况关键在于简化体系。
对于第二种体系类型,即体系与基础连接等于三根链杆(r=3),且满足两刚片规则(不满足两刚片规则时,为几何常变体系,无需机动分析),只需分析体系内部几何不变性即可。将体系内部简化为最多三个刚片(或两个刚片、一个刚片),然后根据三刚片(或两刚片)规则分析几何组成,判断是否为几何不变体系。
(四) 四种简化方法
(1)结构体系内部几何不变部分可以简化为一个刚片。常见的如铰结三角形可简化为一个刚片,在此基础上,看能否增加二元体等,将刚片扩大,直至该刚片不能再扩大为止。
(2)只有两端是铰的折杆、曲杆等其它形状的杆可以简化为一根链杆。
(3)连接两个刚片的两根链杆可以简化为一个虚铰。
(4)可以拆除二元体,简化体系。
二、 机动分析步骤
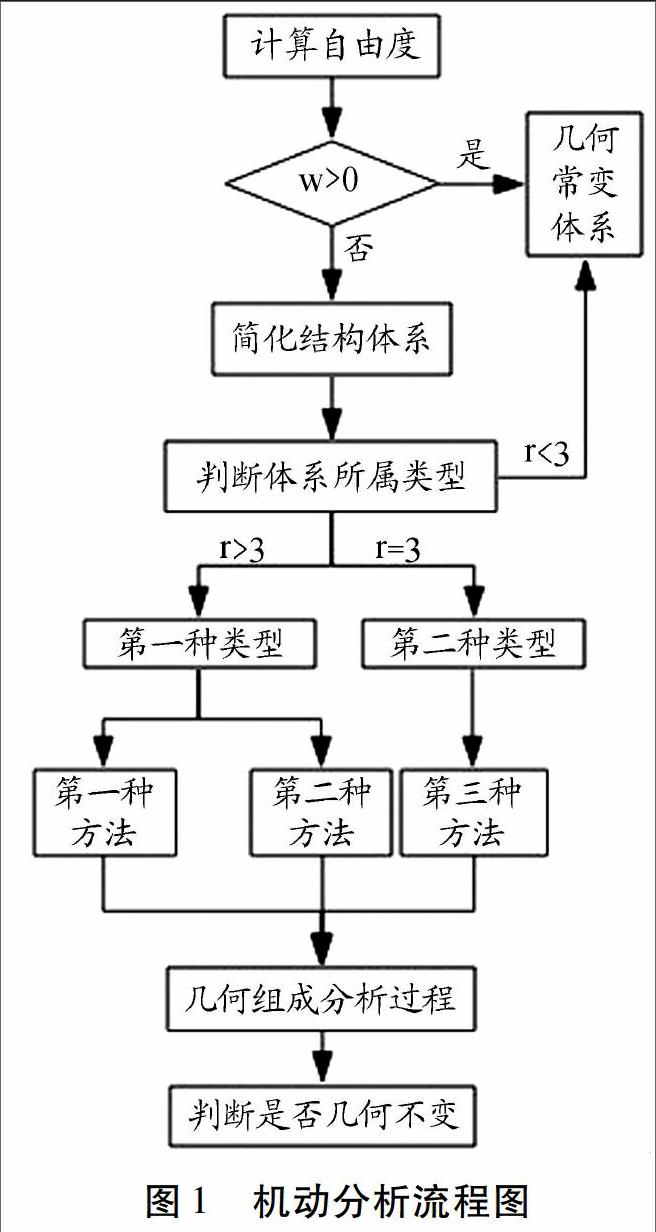
平面体系机动分析的步骤及流程,如图1所示。
(一)计算自由度
用以判断体系屬于刚片体系还是链杆体系。刚片体系的自由度计算公式:w=3m-2h-r;链杆体系的自由度计算公式为:w=2j-b-r。采用自由度公式计算w,若w>0,体系一定几何可变;若w≤0,满足几何不变的必要条件,则需要进行机动分析。
(二) 几何组成分析
(1)简化体系。判断体系是否有二元体,若有先拆除二元体;两端是铰的折杆、曲杆等,杆简化为一根链杆。
(2)判断体系所属类型。根据体系划分标准,判断该体系属于第一还是第二种类型。
(3)选择机动分析方法。根据体系所属的类型和三种分析方法的要求,选择该体系的机动分析方法。
(4)几何组成分析过程。平面体系为第一种类型第一种分析方法的具体分析过程,见算例1。第二种分析方法的具体过程,见算例2。平面体系为第二种类型,应采用第三种分析方法,具体分析过程见算例3。
(5)判断体系是否几何不变。根据两刚片规则或者三刚片规则判断该体系的几何不变性。
三、 算例分析
(一)算例1
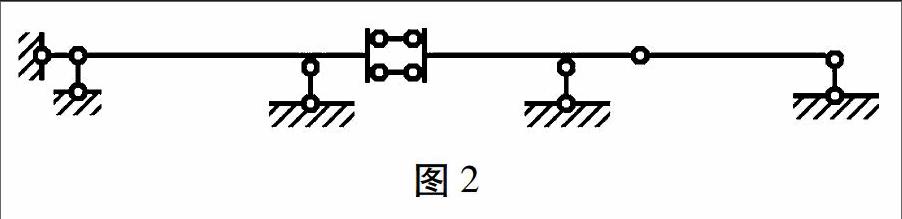
对图2所示体系进行机动分析。
解:(1)计算自由度
该体系属于刚片体系,计算自由度:w=3m-2h-r=3×3-2×2-5=0。
(2)几何组成分析
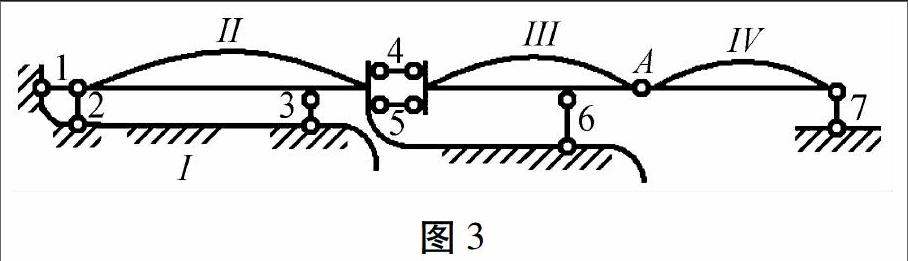
该体系用五根链杆与基础连接,属于第一种类型。首先把基础作为刚片Ⅰ,从刚片Ⅰ开始, 增加二元体1-2,扩大刚片Ⅰ,刚片Ⅰ与刚片Ⅱ之间用一个单铰和一个不通过此铰的链杆3相连(图3)。根据两刚片规则,刚片Ⅰ与刚片Ⅱ组成几何不变部分,即体系局部可以与基础构成几何不变,应采用第一种分析方法,分析过程如图3所示。由地基(刚片Ⅰ)开始,它与刚片Ⅱ看作一个刚片,即将刚片Ⅰ扩大至刚片Ⅱ;该刚片与刚片Ⅲ之间又由不交于一点的链杆4、5、6相连,组成几何不变的部分,继续扩大刚片Ⅰ至刚片Ⅲ;它与刚片Ⅳ之间由铰A和不通过铰A的链杆7相连,组成几何不变部分;最终,刚片Ⅰ扩大至整个体系。所以,该体系为几何不变,且无多余约束。
(二)算例2
对图4所示体系进行机动分析。
解:(1)计算自由度
该体系属于链杆体系,计算自由度:W=2j-b-r=2×8-12-4=0。
(2)几何组成分析
该体系用四根链杆与基础连接,属于第一种类型。首先把基础作为刚片Ⅰ,简化体系,并拆除二元体11-12。从刚片Ⅰ开始,先扩大刚片Ⅰ,依次增加二元体7-8、9-10、5-6,至此刚片Ⅰ不能再扩大,也无法扩大至整体。因此,该体系机动分析应采用第二种分析方法。然后,将其余结构简化为一个或两个刚片。将铰接三角形作为刚片Ⅱ,刚片Ⅱ也无法再扩大,此时由分析可知,不满足两刚片规则要求,且有多余的链杆。因此,需要再选择链杆13为刚片Ⅲ。此时, 刚片Ⅱ、Ⅲ之间由链杆1、2组成的虚铰O1相连。刚片Ⅰ、Ⅱ之间由铰O3相连,刚片Ⅰ、Ⅲ之间由链杆3、4组成的虚铰O2相连,O1、O2、O3三铰不在一直线上。所以,该体系几何不变,且无多余约束(图5)。
(三)算例3
对图6所示体系进行机动分析。
解:(1)计算自由度
该体系属于刚片体系,计算自由度:W=3m-2h-r=3×5-2×6-3=0。
(2)几何组成分析
该体系与基础用三根链杆连接,且满足两刚片规则,属于第二种类型。因此,应采用第三种分析方法,只需要分析体系内部(图7)几何不变性,即把体系内部简化为最多三个刚片。首先选择3、4、5、6作为一个刚片,且该刚片可以扩大,依次增加二元体14-13、21-23,最后体系内部扩大为一个刚片。所以,该体系几何不变,无多余约束。
四、 结 语
根据学生在学习平面体系机动分析中遇到的问题,归纳和总结教学方法和技巧,提出平面体系“2+2+3+4”机动分析模式,较好地解决了学生初学时感到无从下手的难题,使平面体系机动分析过程可以按照一定的模式和步骤进行。按照“2+2+3+4”机动分析模式,通过教师的课堂讲解和课后一些题目的练习,学生反映该模式解题和分析效果较好。
参考文献:
[1]邱秀梅,戴景军,孙建武.平面体系几何组成分析的方法技巧[J].力学与实践,2009,31(2):80-82.
[2]张琳楠,徐春晖,秦太验.平面体系机动分析的一般方法[J].力学与实践,2014,36(6):738-741.
[3]鲁彩凤,鲁凤弟.從几何组成分析中找到结构内力分析的方法[J].高等建筑教育,2012,21(5):101-104.
[4]李廉锟.结构力学(上册)[M].5版.北京:高等教育出版社,2010.
[5]龙驭球,包世华.结构力学I[M].3版.北京:高等教育出版社,2012.

