离心鼓风机用磁轴承的设计

张钢，黄阳，倪晓艇，孔奎，周靛

（上海大学 机电工程与自动化学院 轴承研究室，上海 200072）

离心鼓风机运行能耗占污水处理厂总能耗的50%～60%［1-2］，提高其运行效率对国民经济的发展意义重大。提高离心鼓风机电动机中支承系统的机械效率可以有效提高电动机效率。目前在离心鼓风机中应用的磁悬浮轴承主要是主动磁悬浮轴承。永磁悬浮轴承工作时通过永磁体间的磁力来平衡外载荷，可以实现高转速、高效率运行［3］；同时永磁悬浮轴承支承不需要高压气泵和电子控制系统，使其在工业应用成本上优于气悬浮轴承和主动磁悬浮轴承支承。

现设计一种永磁悬浮轴承，分析其运动特性，并通过试验验证承载力，研究其理论计算公式。

1 产品要求

1.1 电动机整体示意图

设计的电动机结构示意图如图1所示。离心鼓风机在工作状态下会产生垂直向上的2 953.72 N气动力，永磁悬浮轴承所需要承受的轴向载荷2 540.75 N为转子重力412.97 N与气动力的合力。

图1 电动机结构示意图Fig.1 Structure diagram of motor

1.2 永磁轴承设计准则

永磁轴承的设计应该与电动机的设计相匹配，在设计过程中主要考虑以下因素：承载、装配、精度、高速和寿命［4］。因此要求永磁轴承在承受系统气动力与重力的合力Fa时实现悬浮；同时要满足工作转速16 050 r／min，且系统轴承寿命大于5年。

2 建模及仿真

双磁环的结构形式具有最好的承载特性且节省材料［5］，因此选择该结构进行设计，运用分子电流法计算永磁环的力学特性。

2.1 磁力解析模型的建立

轴向永磁轴承结构如图2所示，两永磁环之间的磁力可等效成下磁环内外侧表面a，b上的闭合电流环路与上磁环内外侧表面c，d上的闭合电流环路之间的磁力矢量和。图中，两永磁环磁化方向相反，且中心轴相互平行，R1，R2分别为下磁环内、外半径；R3，R4分别为上磁环内、外半径；e0为两磁环中心线距离；L1为下磁环厚度；L2为上磁环厚度；L为两磁环间隙；p为电流环l1上的任意一点；q为上磁环外表面d上的任意一点；h为q点距上磁环下端面的距离。表面a，b，c，d分布有环形电流，且a与d，c与b表面上的环形电流流向相同。分子电流模型如图3所示，α，β分别为点p，q在各自坐标系中与 x（x′）轴的夹角；r为点 p到点q的矢径。

图2 经典轴向永磁轴承结构图Fig.2 Structure of classic alaxial magneticbearing

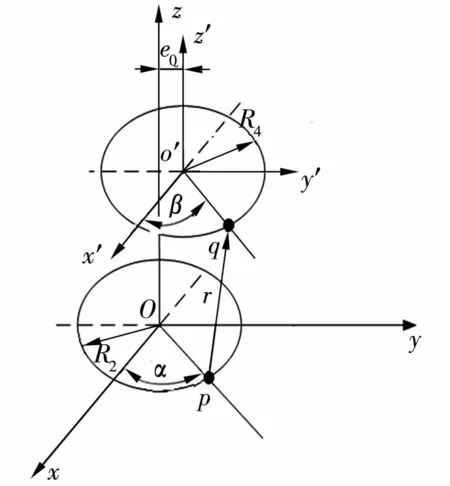
图3 分子电流模型图Fig.3 Model diagram of molecular current

bd面、ac面、ad面、bc面之间的轴向磁力分别为［6］

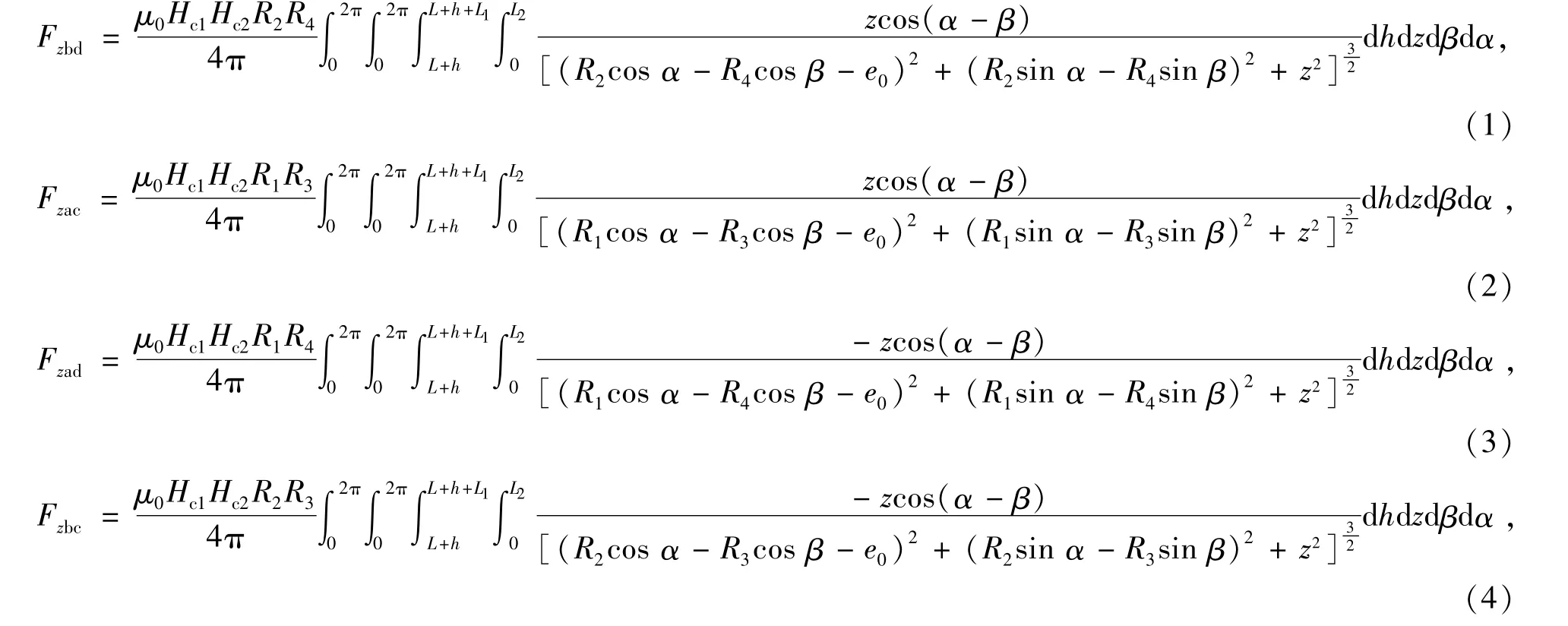
式中：Hc1，Hc2分别为下磁环和上磁环的矫顽力；μ0为真空磁导率，μ0＝4π×10-7H／m。

令L＝L0-Z（L0为两磁环的原始间隙；Z为下磁环向上的轴向位移，上磁环固定），则该永磁轴承的轴向承载力Fa（即两磁环间磁力Fz）为

2.2 磁环设计及优化

根据电动机与叶轮轴连接处φ73 mm的限制条件，将（5）式通过MATLAB编程，经过多次计算和分析得到以下磁环尺寸：R1＝40 mm，R2＝67 mm，R3＝40 mm，R4＝67 mm，L1＝L2＝27 mm，L0＝1.5 mm，两磁环中心线重合，e0＝0。永磁环力学特性曲线如图4所示。

图4 永磁环力学特性曲线图Fig.4 Mechanics characteristic curve of permanent magnet ring

从图4可以看出，对于该尺寸的双磁环永磁轴承，在气隙从1.5mm逐渐减小到0.1mm的过程中，当轴向位移Z＝0.13mm时，其轴向承载力刚好约为2 540.75 N，即此时永磁轴承已实现悬浮。随着位移的增大，刚度也随之增大，表示轴向稳定较好，符合设计要求。

轴向位移Z＝0.13 mm时两磁环间磁力的ANSYS分析结果如图5所示。从图中可以看出，磁感线大部分聚集在两磁环之间，两磁环附近的磁感线密度最大，即磁力最大。

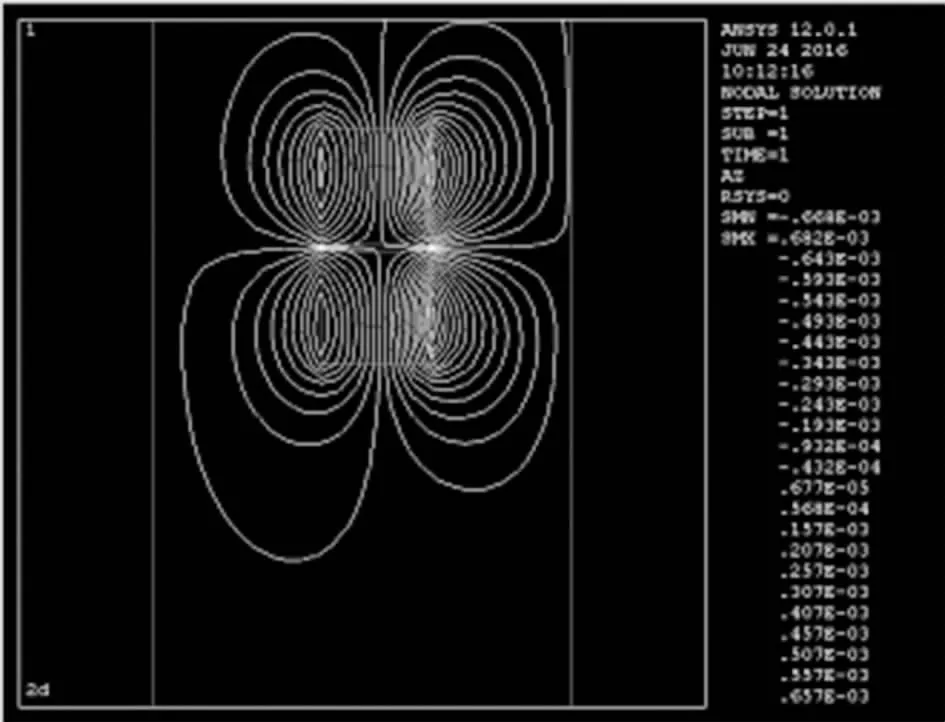
图5 Z＝0.13mm时两磁环磁力分析图Fig.5 Diagram of magnetic analysis of two magnet rings with Z＝0.13 mm

高速旋转的永磁环允许的最大圆周线速度为［7］

式中：σs为材料的屈服极限；ρ为材料密度；ν为材料泊松比；ns为安全系数。将（7）式中的最大圆周线速度转换为转速，其表达式为

式中：D为圆盘外径。钕铁硼磁环的参数见表1。

表1 永磁环参数Tab.1 Parameter of permanent magnet ring

将表1中的参数代入（8）式可得永磁环允许的最大极限转速为nmax＝16 607.6 r／min，超过电动机转速（16 050 r／min），永磁体存在破裂的危险，因此采用不锈钢环来提高磁环强度。

在磁环外层包裹一层4.5 mm厚的不锈钢（1Cr18Ni9Ti）环套后的应力分布如图6所示。其中应力最大区域在不锈钢环套内侧约为115.1 MPa（图6a），远小于不锈钢材料的抗拉强度（550 MPa）；磁环最大应力为73 MPa（图6b），小于材料的屈服极限（82.4 MPa），满足要求。因此在磁环外侧增加保护套有利于优化磁环应力分布。

图6 加保护套后应力分布Fig.6 Stress distribution after adding protection

2.3 永磁悬浮轴承的运行特性分析

通常给定下磁环的运动范围为Z＝0～1 mm（辅助保护轴承保证磁环间的工作间隙为1.5～0.5 mm），相应的承载力范围为2 500～2 800 N，超出该范围的载荷由辅助保护轴承承担。由图4可知，永磁悬浮轴承要在Fa＝2 540.75 N时实现悬浮，此时下磁环向上位移Z＝0.13 mm，磁环间距离由原始间隙1.5 mm缩小为1.37 mm，电动机旋转部分处于悬浮状态，轴向满足承载要求。

双环中心线在不同偏移下的力学特性曲线如图7所示。由图7a可知，随着偏移距离的增大，轴向承载力整体下降，但在偏移量固定情况下，轴向承载力随着位移的增大而增大的趋势是不变的，因此当磁环存在偏移时，也可以承受轴向载荷。由图7b可知，偏移量为0时，径向力始终为0；随着偏移量增大，径向力为负值，且其绝对值越来越大，由此可见，当存在偏移时，是无法承受径向载荷的。此外，在小偏移（偏移量不超过0.1 mm）情况下，径向不平衡力远小于75～320 N，在磁悬浮轴承中，该力加载到辅助轴承上，由于其值远小于辅助轴承的额定动载荷（35.35 kN，约为千分之一），因此辅助轴承在微小载荷的作用下可以达到长寿命的目标。

图7 不同偏移下力学特性曲线Fig.7 Curve of load characteristic with different migration

3 永磁环加载试验及承载力验证

为了能有效测得永磁环的轴向承载力和轴向刚度，从而验证利用分子电流法所计算得到的永磁环承载力的正确性，开展试验研究。永磁环磁力试验原理图如图8所示。首先，将永磁环通过两端螺母与轴固定，设置初始间隙；其次，通过螺旋加载方式对永磁轴承下磁环施加向上的载荷，此时下磁环有向上位移；最后，通过塞尺测定加载后两磁环间隙L′，同时使用力传感器测出此间隙下载荷值。试验装置实物如图9所示。

图9 永磁结构承载力测量试验装置Fig.9 Test device of loading capacity measurement permanent magnet structure

测量时选取初始间隙L0为3 mm，载荷值可以直接读出，塞尺测量时分别选择2个对称点测量以便尽量减小误差。将两点测量值的平均值作为试验结果，将两磁环间隙值转换成轴向位移，试验值与分子电流法计算的理论值及ANSYS仿真值对比如图10所示。从图中可以看出，ANSYS仿真值最贴近试验数据，但是由于过程比较复杂，因此在进行简单磁环磁力分析时较为繁琐。分子电流法虽然没有ANSYS分析的准确，但可采用Monte Carlo积分算法进行编程省去求解步骤，所以在进行简单磁环结构磁力分析时，该方法显示出结果准确、计算方便的优势。

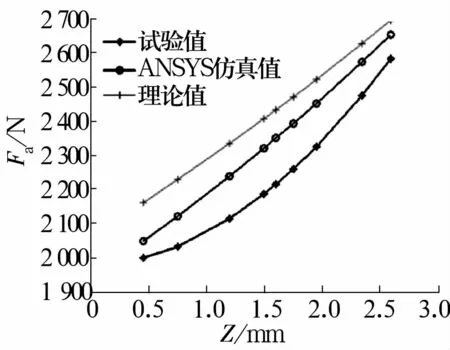
图10 力学特性曲线对比图Fig.10 Contrast of curve of mechanics characteristic

从图10可以看出，分子电流法理论计算出的磁力曲线与试验数据拟合出的磁力曲线变化趋势相同，但其最大误差为11.3%，略大于工程应用要求（10%以内）。因此需对分子电流理论计算出的磁力值进行修正，参考文献［3］中两磁环间磁力计算公式，修正后的磁力公式为

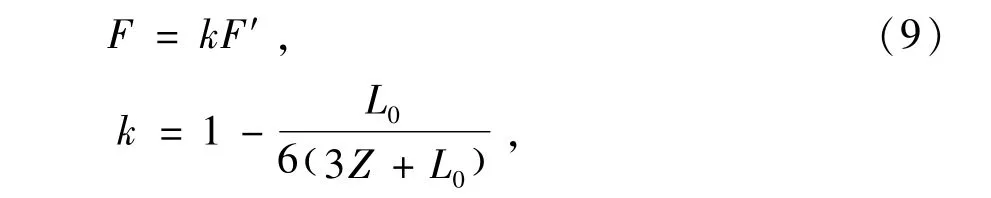
式中：k为修正系数；F′为分子电流理论计算的磁力值。

计算可知，修正后磁力计算值与试验值比较接近，且最大误差4.73%小于工程应用要求。因此，总结出两永磁环间磁力计算的工程应用经验公式为

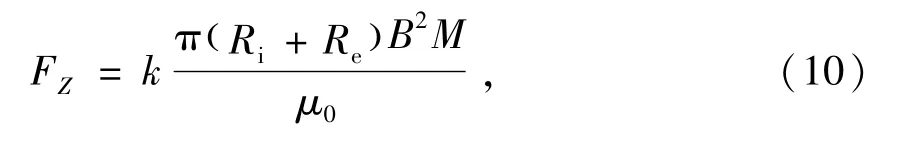
式中：Ri，Re分别为永磁环的内、外半径；M为永磁环的宽度；H为永磁环的厚度；Br为永磁环的剩磁。利用经验公式求解的磁力值与试验值的对比见表2。

表2 经验公式磁力计算值与试验值对比Tab.2 Comparison of empirical formula calculated values and experimental values of magnetic force

由表2可知，使用经验公式所求磁力与试验值最大误差为5.8%（小于10%），经验公式主要是为了对两磁环间的磁力进行估算，故该相对误差是可以接受的。在设计轴向永磁轴承时，只要已知各结构参数，就能利用工程应用经验公式计算出永磁轴承的承载力，便于工程技术人员对永磁环结构的选用，大大简化了设计过程。

4 结束语

设计了一种能够应用于额定功率为250 kW、转速为16 050 r／min的离心鼓风机电动机的轴向永磁轴承，根据立式鼓风机电动机的具体工况要求提出永磁悬浮轴承的设计准则，运用搭建的解析模型设计并优化磁环结构，对永磁轴承的运行特性进行分析，并通过试验证明，利用分子电流法所计算的永磁环承载力与实际测量值之间的误差略大于工程应用要求。对承载力的理论公式进行修正，利用修正公式得到的永磁环承载力与实际测量值之间的误差小于10%，为以后经典轴向永磁轴承的设计提供方便。