结构动内力计算的一种新方法
林 松
(中国航天建设集团有限公司 第二设计分院,北京100071)
结构动内力计算的一种新方法
林 松
(中国航天建设集团有限公司 第二设计分院,北京100071)
首先对振型叠加法进行研究,得出改进的振型叠加法,用改进后的振型叠加法计算的挠度与精确解完全相同.用改进后的振型叠加法对结构动内力进行了分析和计算.
振型叠加法;挠度计算;动内力计算
0 引 言
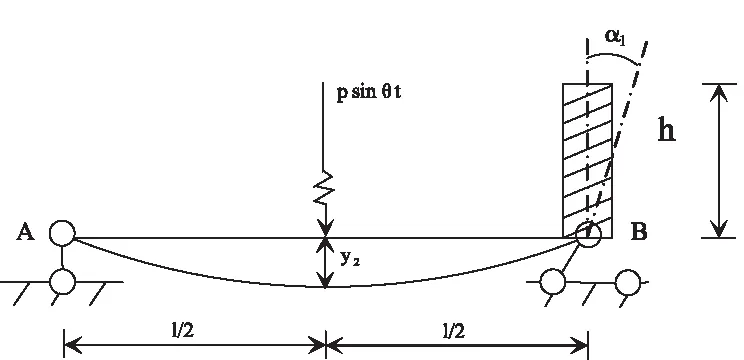
图1
本文首先用一般振型叠加法计算一个简支梁的动位移.计算发现此解答对于有质量处位移是正确的,而对无质量处位移是错误的.然后本文对一般振型叠加法进行了改进,改进后计算无质量处位移与精确解相同.最后用改进后的振型叠加法对结构动内力进行分析计算.
1 计算实例及改进后的振型叠加法
现设图1的梁右端质量m=100 kN;P=1 kN,抗弯刚度EI=1,θ=1 rad/S,由振型叠加法解得动位移解:
(1)
为了验证其正确性,现用结构力学中列动力方程的方法得出该问题的精确解为:
(2)
从上述计算结果发现用结构力学振型叠加法只是计算有质量点的位移是正确的,而计算无质量点的位移是错误的.为了解决这个问题把该梁右端变成固定端,并将力P作用于梁中点,如图2所示,然后由结构力学解得此一次超静定梁的静位移为:

图2

(3)
则以此位移为幅值的动位移为:
(4)
把用振型叠加法计算出的动位移(1)式和图2所计算出的改进项(4)式相加,得到与该问题精确解(2)式相同的解答为
(5)
通过以上计算得出结论,用改进后的振型叠加法可以计算出没有质量处的位移.
2 结构动内力的计算
上述方法还可以精确解出结构的动内力,根据上述原理和方法给出结构动内力的计算过程是
第一步:由振型叠加法算出结构动位移,然后求出结构的动内力.
第二步:把有质量处的位移约束住,再算出动力荷载幅值作用下的静内力.
第三步:把上述两个步骤计算出的两种动内力相加,这就是该结构的最后动内力.
算例 为了使计算简便,对图3(a)所示梁设外荷载P1=4,P2=2,梁抗弯刚度EI=1000,l=5,质量m=1,动力荷载的频率θ=4.(单位:吨·米·秒)

图3
解
(1)用振型叠加法求梁的动内力
该结构的固有频率为
自由度为
{y}=[y1,θ1,y2,θ2]T
则度距阵及质量矩阵为
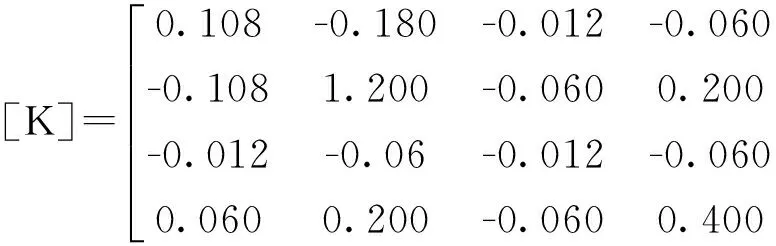
按振型方程[K-ω2]{y}(1)=0解得振型{y}(1)为
{y}(1)T={1,0.3,4,0.3}
正则坐标下的微分方程
其中

则
得动位移为

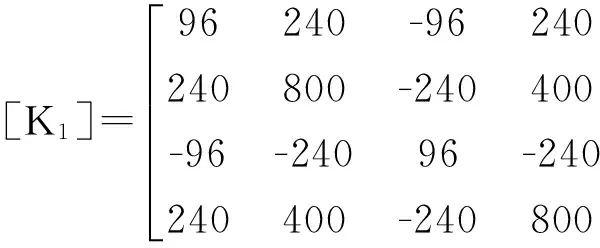

(2)求修正内力值的计算

(3)结构最终内力的计算
3 结 论
本文的方法解决了用振型叠加法计算无质量处位移的问题,同时用该方法还可以精确地计算出结构的动内力.方法简便易行,是结构动力计算的一种有效并值得推广的好方法.
[1]朱慈勉,结构力学(下)[M].高等教育出版社,2004.1
[2]朱伯龙,张琨联.建筑结构抗震设计原理[M].同济大学出版社,1994
[3]崔玉红,严宗达,聂永安.结构中复杂动力系统处理方法的探讨[J].工程力学(增刊),1997
[4]李丽华,毛毳.非对称己型连体建筑连廊风载动力特性分析[J].天津城建大学学报,2016.3
A New Method For Calculating Dynamic Internal Force Of Structures
LINSong
(The Second Design Branch,China Aerospace Construction Group Co.,Ltd.Beijing 100071)
In this paper,superposition of vibration mode is firstly researched,and the modified superposition of vibration method is achieved,by which the deflection is identical to accurate solution.Then,dynamic internal force of structures is analyzed and calculated by the modified one.
superposition of vibration mode;calculation of deflection;calculation of dynamic internal force
2016-10-12
林松(1979-),男,高级工程师,从事建筑结构设计及研究.
10.3969/j.issn.1008-4185.2017.02.009
TU 3
A

