质量比对二自由度圆柱涡激振动影响的计算研究

章大海,王文颢,石凡奇,郝木明

(中国石油大学化学工程学院,山东青岛266580)

质量比对二自由度圆柱涡激振动影响的计算研究

章大海,王文颢,石凡奇,郝木明

(中国石油大学化学工程学院,山东青岛266580)

利用Fluent平台的用户自定义程序(UDF)以及动网格模型,实现圆柱运动方程的一种迭代求解算法,对二自由度弹性支承圆柱体在一定约化速度下的涡激响应进行数值模拟;探讨不同质量比对涡激响应升力的影响。研究表明:采用的迭代求解算法能对弹性支承圆柱涡激振动做出合理预测;质量比对涡激响应的升力影响显著,不仅低质量比圆柱产生的振幅更大,低质量比较高质量比能产生更大的升力系数,且升力相对横向位移的“相位突跳”现象对应的约化来流速度U*更大;圆柱运动轨迹从最初的弧型转变至“8”字型,而后“8”字型逐渐消失并转变为水滴形。

涡激振动;流固耦合;质量比;数值模拟

涡激振动对长输管道、高耸结构、输电线路等设备易产生疲劳破坏,其研究方法主要为基于相似原理的实验研究和基于数值计算的模拟研究。Williamson[1-2]、Sarpkaya[3]和Gabbai[4]等已对涡激振动进行了相关综述;Williamson等[5-9]以低质量比的振动系统为研究对象,通过大量的实验研究发现质量-阻尼联合参数m*ζ对振动幅值有明显的影响,当涡激振动发生在空气中,即m*ζ较大时,振幅曲线只有“初始支”和“下支”两支响应,而在低质量比的水中时,振幅曲线出现三支响应,也就是经典的三支曲线:初始支、上支和下支,且在低质量比情形发现一种对应最大横向振幅的“2T”模态。计算流体力学在涡激振动领域已成为一种主要的研究方法,而基于RANS方程的雷诺时均方法更是被大量研究者所采用。Bahmani等[10]用涡量-流函数法处理N-S方程,模拟层流情况下的圆柱涡激振动,验证了该方法的有效性;潘志远[11]利用RANS方法研究了圆柱体横向自激振动与受迫振动的机理并精确预测了圆柱体的振动;黄智勇等[12]对二自由度圆柱涡激振动进行了数值模拟,发现在质量比低于3.5时,二自由度圆柱的横向振幅比限制流向振动的单自由度时的横向振幅大。林琳等[13]比较了弹性支承圆柱与固定圆柱涡激振动的尾流,分析了振动对流体力系数、壁面压力等参数的影响;董婧等[14]通过数值模拟研究了低雷诺数下圆柱体振动的影响参数及尾涡结构与气动力的关系,并观察到“拍”和“相位开关”等现象。章大海等[15]数值模拟研究了弹性支承圆柱体的涡激振动响应,实现了单自由度振子方程的简单迭代求解。笔者在文献[15]的基础上,进一步研究二自由度弹性支承圆柱体在一定约化速度范围内的涡激响应振幅、频率、升阻力系数、泻涡模式、运动轨迹等,分析不同质量比对涡激响应升力的影响。

1 计算模型

1.1 几何模型

图1为采用二自由度弹性支承圆柱振动系统简化物理模型。采用与文献[15]相同的几何模型,圆柱直径D,圆柱中心距离上、下及左边界的距离为10D,距离右边为20D,以保证尾涡的充分发展;总网格数约1.8×104个。考虑到圆柱运动时,周边网格的不规则重构,在圆柱周围布置1D厚度的结构化网格,并让其随圆柱一起运动,以保证圆柱附近流场的计算精度,如图2所示。具体的边界条件、流体物性等参数的设置参阅文献[15]。

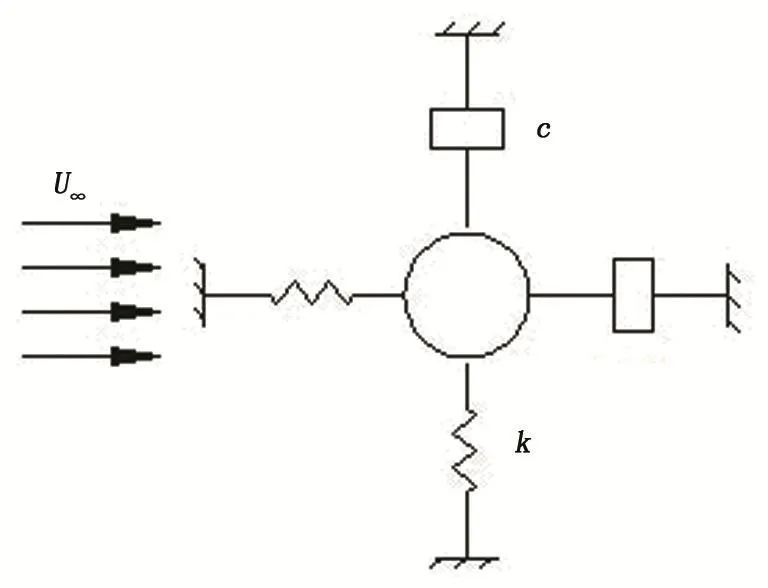
图1 几何模型示意图Fig.1 Model sheme of elastically mounted cylinder

图2 圆柱附近网格Fig.2 Grid near cylinder

1.2 结构动力学方程

对于图1中的双自由度(2-DOF)弹簧-质量-阻尼系统,其控制方程为

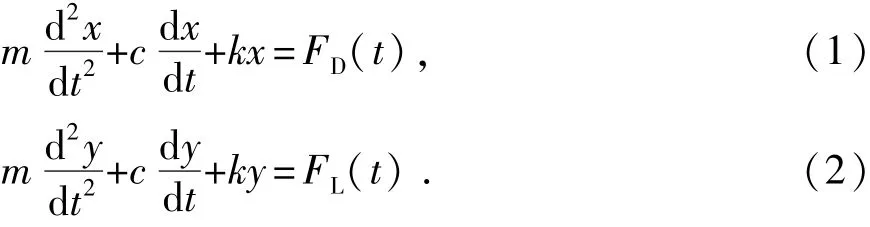
其中,x、y、m、c和k分别为圆柱顺流向位移、横向位移、圆柱质量、结构阻尼系数和系统刚度系数;FD(t)和FL(t)为圆柱所受顺流向和横向流体力,进行无量纲化后可得

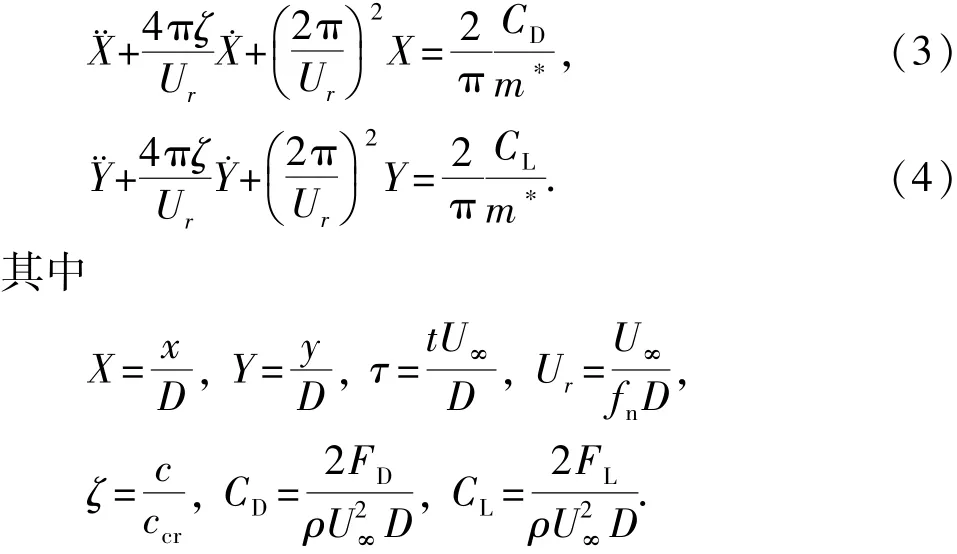
式中,U∞为来流速度;fn为系统固有频率;D为圆柱直径;m*为质量比(m*=m/md,md为圆柱排开的水的质量);ζ为阻尼比;ccr为系统临界阻尼,;CL、CD分别为升、阻力系数;ρ为流体密度。式中导数是关于无量纲时间τ的求导。

1.3 计算流程

二自由度圆柱的运动须将顺流向的方程(3)和横流向的方程(4)同时进行求解,先将式(4)简化为如下形式:

据(8)～(11)利用迭代思想就可进行二自由度涡激振动的求解。编写代码时,给定初始速度为0 m/s,在每时间步只须提取流体力FL、FD,根据方程(8)～(11)求解圆柱的运动速度,根据Fluent里的用户自定义函数(User-Defined Functions),通过Define_CG_Motion宏将圆柱的运动速度返回给Fluent主程序,Fluent给UDF返回流体力,实现流体与结构控制方程的耦合求解。

2 二自由度圆柱的涡激响应

图3为计算结果与实验数据的对比,采用约化速度表达式U*=U∞/fnwD进行处理[5],圆柱直径D=0.0381m,质量比m*=2.6,约化速度U*=3～12。

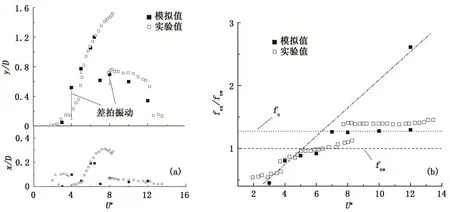
图3 圆柱涡激振动响应曲线Fig.3 Amplitude and frequency response as a function of reduced velocity

由图3可知,横向振幅能明显分辨出初始分支、上端分支、下端分支。最大横向振幅出现在U*=6.4处,振幅值约为y/D=1.22,最大流向振幅发生在U*=6,幅值约为x/D=0.2。横向、流向振幅变化趋势与Williamson[7]的实验结果大体相符。图3(b)清楚地显示了频率锁定现象。在随着U*的增大,横向振动频率由符合Strohal规律,突然转变为锁定在系统在水中自然频率fnw附近,在U*=12出现回归Strohal规律的振动分量,锁定现象开始减弱。可以看出,数值计算与实验结论一致,本文中采用的迭代算法是有效的。实验中没有出现最大横向振幅y/D=1.55,误差为20%。计算采用二维模型以及RANS方法,主观上没有考虑流场的三维特性和湍流的随机性,而文献[12]表明涡激振动泻涡的三维特性以及随机性对振幅均有影响;要实现涡激振动的三维计算并模拟出随机特性,所花费的时间与资源将会成倍增加[11]。另外,采用光滑圆柱进行计算,忽略了表面粗糙度的影响,与实验情况不符,而圆柱的表面粗糙度会使剪切层分离点提前,能够增大涡激振幅[16],造成计算误差。由此可见,本文中的算法是可取的。

图4给出了无量纲位移x/D、y/D,阻力系数CD和升力系数CL随时间变化的曲线。当U*=3.0时,圆柱体的振幅较小;随着约化速度增加,振幅、升力系数曲线发生明显的差拍振动,圆柱体的振幅、升阻力系数幅值明显增大;U*=6时,振幅和阻力系数幅值继续增大,升力系数减小,差拍振动现象消失,发生锁定现象;在U*=12时,振幅减小,锁定现象开始消失,振动重新出现服从Strohal规律的分量。可以看出,圆柱体振动响应与文献结论相符,本文中算法是可取的。

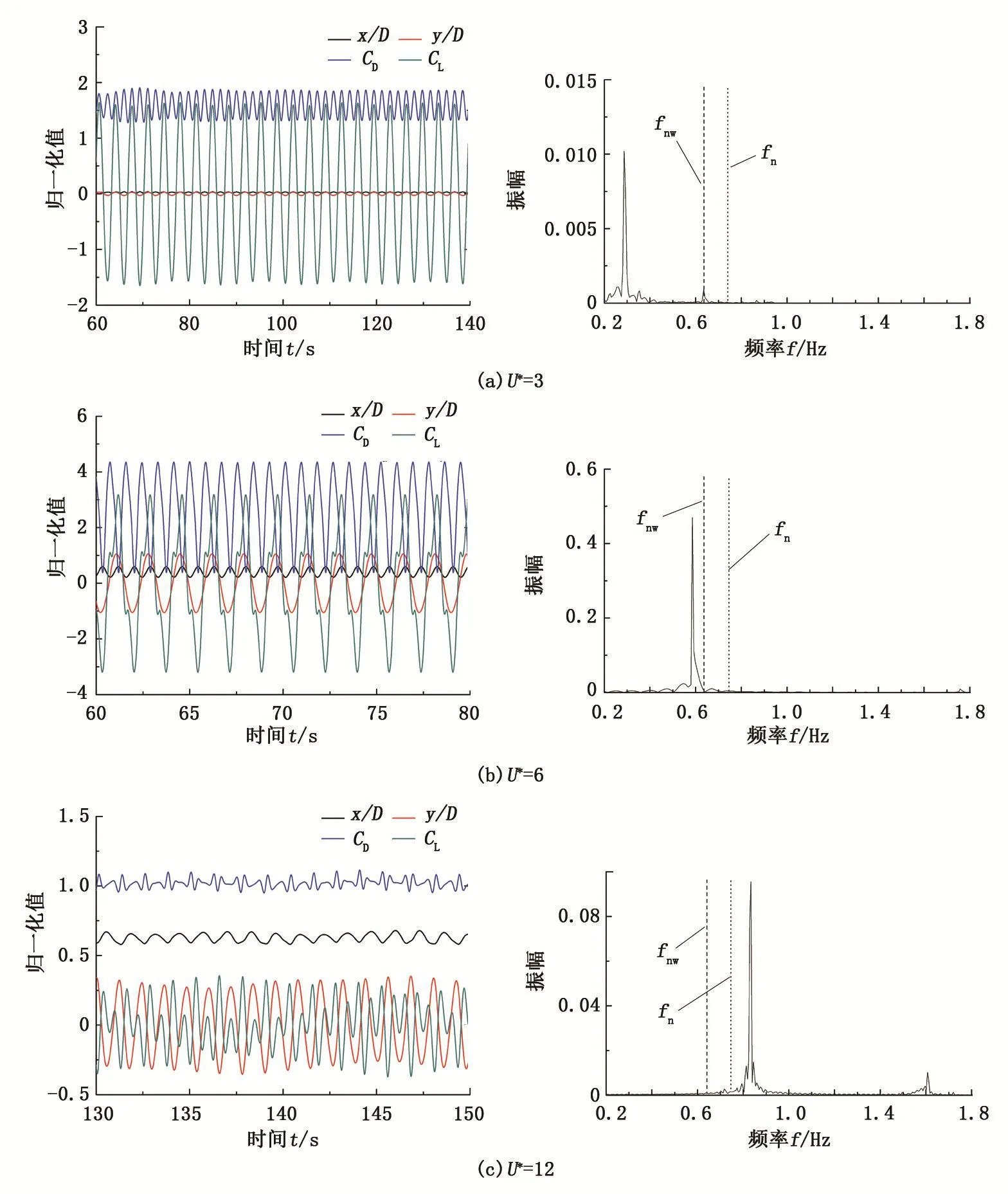
图4 不同约化速度下圆柱的涡激响应时程及对应频谱Fig.4 Amplitude and fluid force response and corresponding spectrum under different U*

图5给出圆柱一个振动周期内(U*=6.4)涡量等值线图清晰地捕捉到了2T泻涡模式。Williamson等[5-9]实验结果表明:低质量比弹性支撑圆柱涡激振动中与振动响应初始分支对应的尾涡为2S模式,而与上端分支对应的尾涡则为2T模式。本文结果与之相符,也验证了计算方法的有效性。图6给出圆柱质心的运动轨迹,从U*=3的弧型转变至U*=6的“8”字型,与文献[17]相符,而后“8”字型逐渐消失,至U*=10时,本文中算法计算的轨迹呈水滴型。

3 质量比对升力系数的影响

研究不同质量比对升力、相对横向位移相位角的影响。分别进行质量比m*为2.6和8.63的圆柱涡激振动数值计算,提取升力系数与横向位移时程,计算升力系数的均方根值,通过Hilbert变换计算出升力相对横向位移的实时相位。计算结果如图7～8所示。

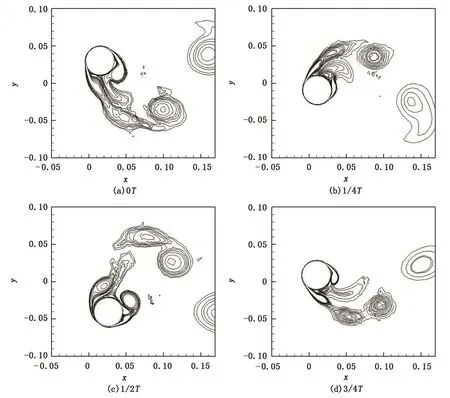
图5 圆柱体单个振动周期内流场尾涡Fig.5 Vorticity magnitude contours within a vortex shedding period

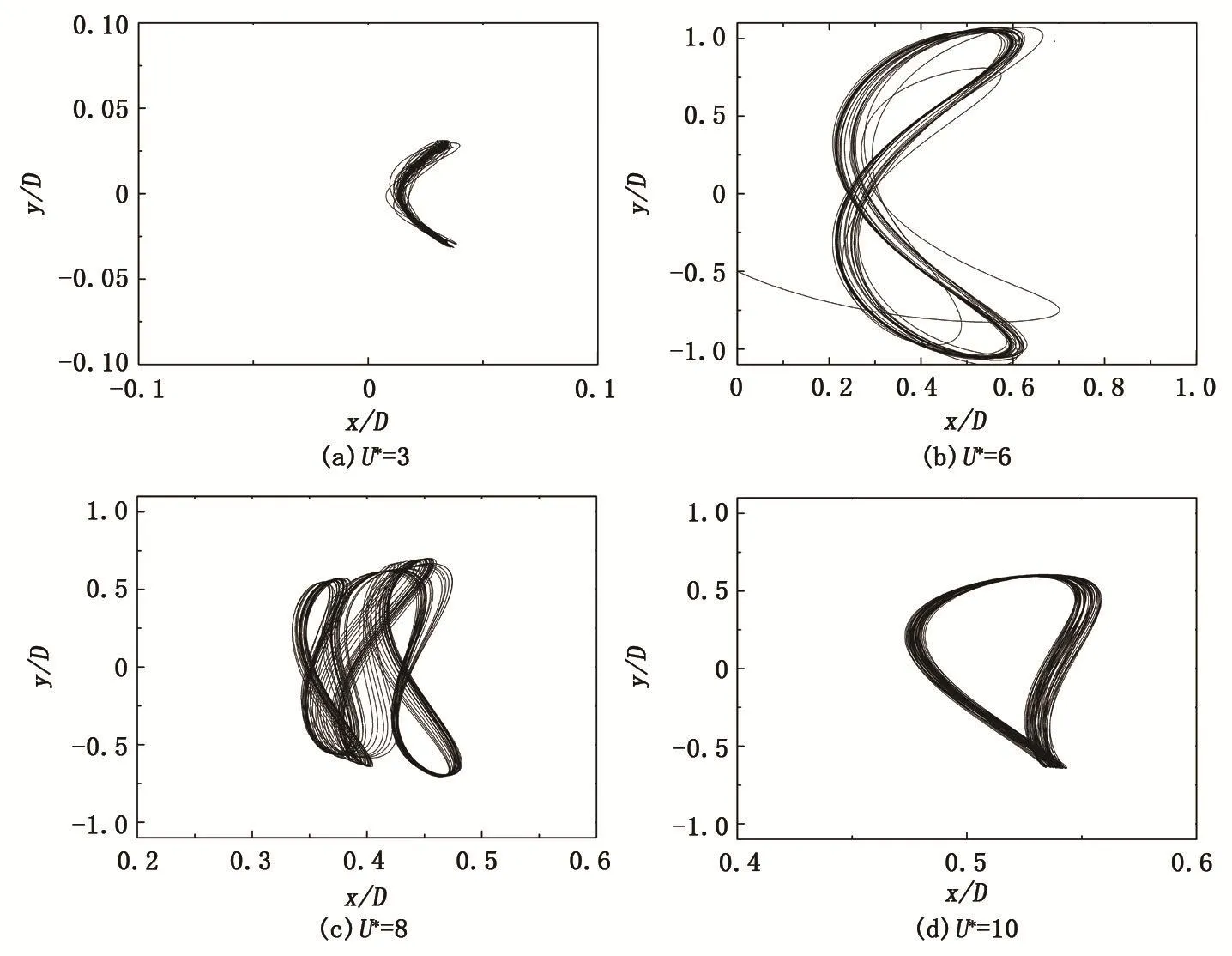
图6 圆柱质心轨迹Fig.6 Cylinder centroid trajectory

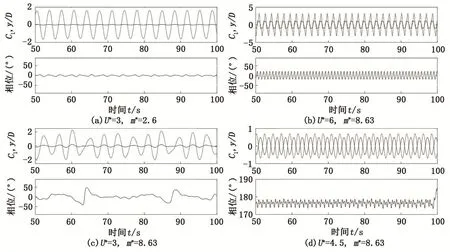
图7 振幅时程曲线和升力系数的实时相位Fig.7 Typical time traces of cylinder displacement and phase

图8 不同质量比下升力系数及相位角Fig.8 CLrmsand phase angle variation with U*

图8(b)中误差条带表示相位值在0°～180°变化,图8由升力系数时程给出升力系数均方根值,升力系数实时相位由Hilbert变换获得。Williamson[5-9]指出,升力系数CL均方根值会随约化速度由小到大变化,最大值出现在初始支与上支的转换区域,在此之后会急剧下降。升力系数相对圆柱位移的相位Φ在初始支和上支为0°,即升力与位移同相,然后“突跳”为180°,即升力与位移反相。本文中得到的两种质量比下的升力系数均方根值变化规律都与实验规律相符,均先增大再减小,m*=8.63给出的升力均方根值峰值在U*=3.5出现,为CLrms=1.15,在U*=4.5即大幅下降至CLrms=0.4;相位的“突跳”区域出现在U*=3.5～4(图8(b));m*=2.6的CLrms峰值2.5在U*=5出现,比m*=8.63的升力系数更大,相位突跳在U*=6～7出线,比m*=8.63情况出现得更晚。

4 结 论

(1)迭代求解算法能够对弹性支承圆柱涡激振动做出合理的预测。

(2)质量比对涡激响应的升力影响显著,不仅低质量比产生的振幅更大,低质量比较高质量比能产生更大的升力系数,且升力相对横向位移的“相位突跳”现象对应的约化来流速度U*更大。

(3)圆柱运动轨迹从最初的弧型转变至“8”字型,而后“8”字型逐渐消失并逐渐转变为水滴型。

[1] WILLIAMSON C H K,GOVARDHAN R.A brief review of recent results in vortex-induced vibrations[J].Journal of Wind Engineering and Industrial Aerodynamics,2008,96(6/7):713-735.

[2] WILLIAMSON C H K,GOVARDHAN R.Vortex-in-duced vibrations[J].Annual Review of Fluid Mechanics,2004,36(1):413-455.

[3] SARPKAYAS T.A critical review of the intrinsic nature of vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19(4):389-447.

[4] GABBAI R D,BENAROYA H.An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J].Journal of Sound and Vibration,2005,282(3/4/5):575-616.

[5] JAUVTIS N,WILLIAMSON C H K.The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J].Journal of Fluids Mechanics,2004,509:23-62.

[6] MORSE T L,WILLIAMSON C H K.The effect of reynolds number on the critical mass phenomenon in vortexinduced vibration[J].Physics of Fluids,2009,21(4):045105.

[7] GOVARDHAN R,WILLIAMSON C H K.Modes of vortex formation and frequency response of a freely vibrating cylinder[J].Journal of Fluid Mechanics,2000,420:85-130.

[8] MORSE T L,WILLIAMSON C H K.The effect of Reynolds number on the critical mass phenomenon in vortexinduced vibration[J].Phisics of fluids,2009,21(045105):1-8.

[9] KHALAK A,WILLIAMSON C H K.Dynamics of a hydroelastic cylinder with very low mass and damping[J].Journal of Fluids and Structures,1996,10:455-472.

[10] BAHMANI M H,AKBARI M H.Response characteristics of a vortex-excited circular cylinder in laminar flow[J].Journal of Mechanical Science and Technology,2011,25(1):125-133.

[11] 潘志远.海洋立管涡激振动机理与预报方法研究[D].上海:上海交通大学,2005.PAN Zhiyuan.Vortex induced vibration of marine riser and response prediction[D].Shanghai:Shanghai Jiaotong University,2005.

[12] 黄智勇,潘志远,崔维成.两向自由度低质量比圆柱体涡激振动的数值计算[J].船舶力学,2007,11(1):1-9.HUANG Zhiyong,PAN Zhiyuan,CUI Weicheng.Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass-ratio[J].Journal of Ship Mechanics,2007,11(1):1-9.

[13] 林琳,王言英.自激振动圆柱体湍流场及发展变化的研究[J].振动与冲击,2013,32(14):164-173.LIN Lin,WANG Yanying.Computation of a turbulence flow and its development around a self-induced vibrating circular cylinder[J].Journal of Vibration and Shock,2013,32(14):164-173.

[14] 董婧,宗智,李章锐,等.两自由度运动圆柱绕流的离散涡方法模拟[J].船舶力学,2012,16(1/2):9-20.DONG Jing,ZONG Zhi,LI Zhangrui,et al.Numerical simulation of flow around a cylinder of two degrees of freedom motion using the discrete vortex method[J].Journal of Ship Mechanics,2012,16(1/2):9-20.

[15] 章大海,石凡奇,王君,等.基于一种固体区域迭代算法的圆柱涡激振动数值计算[J].船舶力学,2016,20(4):430-438.ZHANG Dahai,SHI Fanqi,WANG Jun,et al.Numerical simulation of VIV of a cylinder using an iteration method in calculating cylinder motion[J].Journal of Ship Mechanics,2016,20(4):430-438.

[16] 丁林.被动湍流控制下多柱体流致振动研究[D].重庆:重庆大学,2013.DING Lin.Research on flow induced motion of multiple circular cylinders with passive turbulence control[D].Chongqing:Chongqing University,2013.

[17] SANCHIS A,SALEVIK G,GRUE J.Two-degree-offreedom vortex-induced vibrations of a spring-mounted rigid cylinder with low mass ratio[J].Journal of Fluid and Structures,2008,24:907-919.

(编辑 刘为清)

Calculation study on the influence of mass ratio on VIV of a 2-DOF cylinder

ZHANG Dahai,WANG Wenhao,SHI Fanqi,HAO Muming
(College of Chemical Engineering in China University of Petroleum,Qingdao 266580,China)

An iterative solution algorithm was developed to solve the cylindrical motion equation using Fluent UDF codes and dynamic mesh method,through which the numerical simulation of the vortex-induced vibration(VIV)of a two degree of freedoms(2-DOF)elastically mounted cylinder at a certain reduced velocity.And the influence of different mass ratios on the VIV lift was analyzed.It is found that the iterative solution algorithm can reasonably predict the VIV of elastically mounted cylinder.And the influence of the VIV lift is significant.Compared to high mass ratio cylinders,low mass ratio cylinders can excite higher amplitude,larger lift coefficient,and the phase angle reverse corresponds with a larger reduced velocity U*.The trajectory of the cylinder transfers from the initial arc figure to"8"figure,and finally to a water drop figure.

vortex-induced vibration;solid-fluid interaction;mass ratio;numerical simulation

O 237

:A

章大海,王文颢,石凡奇,等.质量比对二自由度圆柱涡激振动影响的计算研究[J].中国石油大学学报(自然科学版),2017,41(3):169-175.

ZHANG Dahai,WANG Wenhao,SHI Fanqi,et al.Calculation study on the influence of mass ratio on VIV of a 2-DOF cylinder[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(3):169-175.

1673-5005(2017)03-0169-07doi:10.3969/j.issn.1673-5005.2017.03.021

2016-09-22

山东省自然科学基金项目(ZR2012EEQ011)

章大海(1978-),男,副教授,博士,研究方向为流体耦合与CFD的工业应用。E-mail:dhzhang@upc.edu.cn。