装载机驱动桥半轴疲劳强度影响因素分析

覃汝庆，朱江新，覃频频

(广西大学机械工程学院，广西南宁 530004)

装载机驱动桥半轴疲劳强度影响因素分析

覃汝庆，朱江新，覃频频

(广西大学机械工程学院，广西南宁 530004)

在再制造业工程机械领域中，半轴花键产生疲劳裂纹是半轴的主要失效形式，其裂纹特征决定半轴回收件的再制造处理工艺。采用基于缺陷建模的半轴强度分析方法，根据驱动桥半轴回收件裂纹的统计情况，随机选择一组裂纹特征的几何参数，建立齿根裂纹模型，使用ANSYS软件进行有限元静力分析，观察半轴最大等效应力与裂纹几何参数的变化关系及裂纹对半轴强度的影响。

疲劳裂纹；驱动桥半轴；裂纹参数；等效应力

0 引言

驱动桥半轴是装载机传动系统的一个重要组成部分，为了研究驱动桥半轴啮合时裂纹几何参数对花键齿应力应变场分布结果的影响，将建立不同裂纹参数值对半轴花键进行有限元静力分析，对半轴强度分析具有重要意义。

1 驱动桥半轴几何模型及其工况分析

所研究的对象为某装载机驱动桥半轴，材料为20CrMnTi,弹性模量为2.12×1011Pa，泊松比0.293，抗拉强度1 080 MPa，屈服强度835 MPa。半轴花键的主要参数值如表1所示。

表1 某装载机驱动桥半轴花键主要参数

首先在UG软件中对半轴三维几何模型进行参数化建模，然后导入到ANSYS中进行有限元分析。装载机半轴在工作过程中主要受到扭矩作用，半轴所受的载荷来自于半轴齿轮，即通过半轴上的外花键与半轴齿轮相啮合来传递扭矩[1]。为了提高计算效率，在不影响计算结果的情况下，对模型进行简化，取右端花键。简化后的半轴模型如图1所示。

图1 简化的半轴三维模型

2 花键齿根裂纹的引入

2.1 驱动桥半轴最恶加载位置的确定

装载机的工作环境复杂，半轴在外载荷的作用下，受到最大扭矩时，其所受应力为500 MPa[2]。受扭时应力集中在半轴花键不连续的拐角处，首先产生裂纹从而生成疲劳问题。由断口微观分析半轴的失效形式，花键齿出现了明显的变形，在承受大的应力时，齿根部分产生与表面平行的裂纹[3]。根据材料力学知识可知，零部件最大内应力处强度最弱，是出现裂纹的危险截面。驱动桥半轴受破坏形式如图2所示。

图2 驱动桥半轴破坏形式

2.2 裂纹几何参数的设置

文献[4]中通过有限元分析得出越往花键齿端的应力值越大，花键退刀槽端部的应力值最大，被视为薄弱部位。花键啮合过程中，花键齿的齿根部分承受较大弯曲应力，因此半轴危险截面处于花键齿根处，根据HOFER提出的30°切线理论[5]来确定，为了分析花键齿齿根裂纹对应力集中的影响，将裂纹沿齿根危险截面分布，如图3所示。

图3 危险截面示意图及裂纹模型

半轴件中的裂纹主要是疲劳裂纹，从裂纹产生到花键磨损过程中，根据文献[6]，裂纹沿着长度、宽度、深度方向扩展。一个完整的疲劳裂纹扩展速率分为3个阶段：第一阶段扩展方向与外力成45°；第二阶段裂纹沿着垂直外力的方向扩展；第三阶段为快速扩展阶段。文献[7]中指出：当应力幅增大时，第一阶段裂纹可长达几个毫米，裂纹的检测能力是0.1 mm。文中设定裂纹宽度，研究裂纹深度和长度对花键齿应力集中的影响，在花键齿齿根危险截面的端面Z=0和Z=L(Z为花键长度)处及中部Z=L/2，分别创建一系列宽度为0.1 mm的微小裂纹，根据裂纹扩展路径[7-8],在深度上取0.1、0.2、0.3、0.4、0.5、1 mm 6个值，长度上取0.5、1、2、5、10、20 mm 6个值，共建立108个带裂纹的有限元分析模型，假定半轴模型其他部分是连续且各向同性的。

3 驱动桥半轴有限元静力分析

为了提高齿轮啮合的计算精度，选择solid186单元类型，半轴花键采用自由网格划分方式，网格精度为6，半轴齿轮划分为六面体网格。半轴花键与半轴齿轮啮合属于内啮合，无裂纹模型简化如图4所示，有裂纹模型如图5所示。设置接触对，根据花键啮合的传动特性施加载荷约束。坐标系设置为全局柱坐标，在半轴花键B面上施加全约束DOF。半轴主要受扭矩载荷，为了更好地模拟载荷，将扭矩转换成节点力施加在半轴齿轮A面的节点上。半轴齿轮半径为0.037 5 m，网格划分后A面上的节点数为552个，半轴花键主要受到半轴齿轮传递的力矩，半轴花键受力公式：

在分析半轴花键齿面接触强度时，要考虑系数的选定：使用系数K1、齿侧间隙系数K2、分配系数K3、轴向偏载系数K4、弯曲强度的计算安全公式SF，参考GB/T 17855-1999《花键承载能力计算方法》中使用系数，齿根许用弯曲力:

[δF]=δb/(SF·K1·K2·K3·K4)=1 080/(1.25×1.25×1×1×1.6)=432MPa

图4 无裂纹模型 图5 半轴端部和中部有裂纹模型放大图

通过有限元仿真模拟，可以得到半轴花键等效应力云图。由图6得出：对无裂纹模型模拟得到的最大等效应力出现在花键齿的齿根部分，花键齿的最大等效应力424MPa，小于齿根许用弯曲应力[δF]。由图7(带裂纹的模型端部Z=L)可知：裂纹宽度为0.1 mm，深度为1 mm，长度为20 mm时花键齿危险截面的最大等效应力为1 140 MPa。

图6 无裂纹模型的等效应力云图

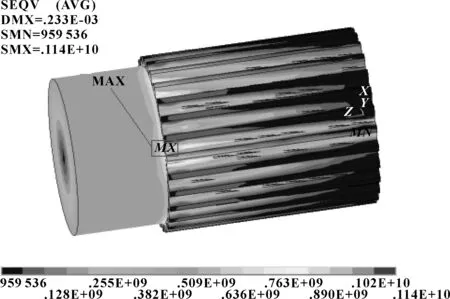
图7 带裂纹模型的等效应力云图

4 结果分析

通过有限元分析，裂纹的最大等效应力与裂纹参数之间的关系如图8、图9所示。

图8 裂纹宽度为0.1 mm、深度取不同值时，裂纹不同分布位置Z=0、Z=L/2、Z=L处最大等效应力随长度变化情况

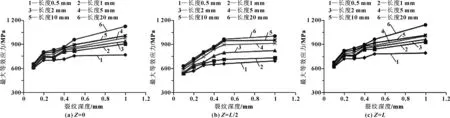
图9 裂纹宽度为0.1 mm、取不同长度时，裂纹不同分布位置Z=0、Z=L/2、Z=L处最大等效应力随深度变化情况

图8、图9显示了半轴花键在裂纹宽度取0.1 mm时，裂纹不同分布位置Z=0、Z=L/2、Z=L处的最大等效应力在裂纹长度和深度方向的变化情况，从图中数据可以得出以下结论：

(1)图6显示的无裂纹花键齿最大等效应力424 MPa与图7显示的有裂纹最大等效应力1 140 MPa相比，添加宽度为0.1 mm、分别取6个深度值(0.1～1 mm)及6个长度值(0.5～20 mm)的裂纹后最大等效应力变化范围为521～1 140 MPa，添加裂纹处有明显的应力集中；

(2)对比图8、9的(a)(b)(c)可以看出：同样的裂纹宽度，端部裂纹Z=0、Z=L处的最大等效应力大于中部裂纹Z=L/2处的最大等效应力，端部裂纹Z=L处最大等效应力大于裂纹Z=0处的最大等效应力，因此端部裂纹Z=L对半轴强度的影响较大；

(3)对比图8、9可以发现：当裂纹宽度一定时，裂纹深度比裂纹长度对最大等效应力的影响强；

(4)由图8、9得出：裂纹处最大等效应力值与裂纹的长度和深度值成正比，长度超过10 mm时，最大等效应力变化平稳。

5 结论

对带裂纹的装载机驱动桥半轴进行了ANSYS静态三维接触分析。根据裂纹长度、深度及分布位置的不同，设置108个带裂纹半轴模型进行有限元分析，模拟出不同参数最大等效应力结果图，分析图表得出裂纹参数与半轴最大等效应力的相互关系，对给出半轴裂纹极限判据具有一定的理论指导作用。

【1】杨占敏，王智明，张春秋.轮式装载机[M].北京:化学工业出版社,2005.

【2】蒙秋红，张丽.某新型装载机前桥半轴断裂失效分析及改进措施[J].工程机械，2009，40(11):59-62. MENG Q H,ZHANG L.Failure Analysis for Semi-shaft Fracture in Front Axle of a New Type Loader and Its Improving Measures[J].Construction Machinery and Equipment,2009,40(11):59-62.

【3】李俊，赵鑫，王温银.20CrMnTi钢花键轴开裂失效分析[J].热处理，2011,26(5):82-84. LI J,ZHAO X,WANG W Y.Analysis on Cracking of 20CrMnTi Steel Spline Shaft[J].Heat Treatment,2011,26(5):82-84.

【4】王继新，胡季，侯晓婷,等.利用载荷谱的轮式装载机半轴有限元分析[J].现代制造工程，2010(5):1-3. WANG J X,HU J,HOU X T,et al.Loader Axle Shaft Finite Element Analysis Based on Load Spectrum[J].Modern Manufacturing Engineering,2010(5):1-3.

【5】李茹贞,赵清慧.齿轮强度设计资料[M].北京:机械工业出版社,1984:15-16.

【6】LEWICKI D G,BALLARINI R.Gear Crack Propagation Investigations[J].Tribotest,1998,5(2):157-172.

【7】王栓柱，金属疲劳[M].福州:福建科学技术出版社，1985.

【8】LEWICKI D G.Effect of Rim Thickness on Gear Crack Propagation Path[R].NASA Technical Memorandum 107229,1996.

【9】LALONDE S,GUILBAULT R.Prediction of Thin-rimmed Gear Crack Propagation from a Factorial Design Approach[J].Fatigue & Fracture of Engineering Materials&Structures,2011,34(7):470-486.

Influence Factors Analysis for Fatigue Strength of Loader Drive Axle Shaft

QIN Ruqing, ZHU Jiangxin, QIN Pinpin

(College of Mechanical Engineering,Guangxi University, Nanning Guangxi 530004,China)

In the remanufacturing field of engineering machinery, a main axle failure mode is crack on root of spline. The crack characte-ristics play a key role in the manufacturing process of the used axle. An axle strength analysis method based on crack modeling was introduced. According to statistics, a group of crack geometry parameters were randomly selected ,then root of axle spline models were built. These models were analyzed with finite element analysis software ANSYS. The relationships between the maximum Von Mises stress in the axle spine and the crack geometrical parameters were analyzed and the effects of cracks on axle strength were also obtained.

Fatigue crack; Drive axle shaft; Crack parameters; Equivalent stress

2016-10-31

广西自然科学基金项目(2015GXNSFAA139280)

覃汝庆(1990—)，女，壮族，硕士研究生，研究方向为机械CAD/CAM/CAE。E-mail：ruqing_qin@163.com。

10.19466/j.cnki.1674-1986.2017.06.006

U463.218

A

1674-1986(2017)06-023-04