基于多核最小二乘支持向量回归的TDOA-DOA映射方法

张 峰 陈华伟 李妍文

(南京航空航天大学电子信息工程学院，南京，210016)

基于多核最小二乘支持向量回归的TDOA-DOA映射方法

张 峰 陈华伟 李妍文

(南京航空航天大学电子信息工程学院，南京，210016)

基于到达时间差(Time difference of arrival, TDOA)估计的方法是声源波达方向(Direction of arrival, DOA)估计中的一类重要方法。其中由TDOA到DOA的映射是该类方法的关键步骤。本文提出了一种基于多核聚类最小二乘支持向量回归(Least-squares support vector regression, LS-SVR)的TDOA-DOA映射方法，并且分析了其稀疏化处理后的性能。为了提高混响噪声环境下的TDOA-DOA映射性能，本文还给出了一种基于归一化中值滤波的TDOA估计离群值消除方法。仿真结果表明，本文提出的方法要优于现有的最小二乘方法以及单核LS-SVR方法。

声源波达方向估计；到达时间差估计；最小二乘支持向量回归；多核学习

引 言

声源波达方向(Direction of arrival, DOA)估计是音频与语音信号处理领域的一个重要研究方向，在视频会议系统[1]、机器人听觉[2]和说话人识别系统[3]等诸多领域具有广泛应用。目前人们已提出了多种声源DOA估计方法[4-9]，其中典型的声源DOA估计方法包括基于到达时间差(Time difference of arrival, TDOA)的方法、基于可控响应功率(Steered response power, SRP)的方法[4-5]以及高分辨空间谱估计方法[6-7]等。相比较，SRP方法和高分辨空间谱估计法需要对目标声源的方位进行全空间搜索，因此计算量较大。而基于TDOA估计的方法，其计算复杂度相对较小。因此，基于TDOA估计的方法得到了广泛研究，成为实际应用中的一类重要方法。基于TDOA估计的声源DOA估计方法利用互相关方法估计出声音信号到达各麦克风的时间差，从而估计出声源DOA。该方法通过两步实现，第1步是TDOA估计(亦称为时延估计)，第2步为TDOA-DOA映射。目前人们提出了很多时延估计的方法提高混响噪声环境下的声源DOA估计性能。相比较而言，对于TDOA-DOA映射的研究尚不够深入。典型的TDOA-DOA映射方法包括最大似然法和最小二乘法。与最小二乘法相比最大似然法的缺点是需要已知估计量的统计特征，而这些信息在实际应用中往往无法预知。因此最小二乘法得到了广泛应用[10]。最小二乘映射方法存在一些局限性：(1)对于非线性阵列不一定能得到闭式解，因而需要进行搜索求解，这使得计算量增大；(2)在声源位于阵列端射方向附近时其性能会急剧恶化。为克服这一问题，文献[11]提出了采用最小二乘支持向量回归(Least-squares support vector regression, LS-SVR)机构造非线性映射，取得了比最小二乘法更高的声源DOA估计精度。此外文献[12]还分析了核函数的选取对LS-SVR映射性能的影响。

现有的基于LS-SVR的TDOA-DOA映射方法仅仅局限于单核函数。单核函数方法虽然可以解决非线性模式分析问题，但在数据异构不规则、样本不平坦分布等复杂情形下，其效果不够理想。多核函数的方法可以克服这一缺点[13]。本文研究了基于多核函数LS-SVR的TDOA-DOA映射方法以提升声源DOA的估计性能。此外针对混响噪声环境TDOA估计精度较低的情况，给出了一种基于归一化中值滤波的TDOA估计值野点消除方法。考虑到多核LS-SVR方法的训练集均为支持向量，本文通过稀疏化处理降低了训练集中冗余支持向量的计算量。

1 基于LS-SVR的声源TDOA-DOA映射方法

考虑由M个全向麦克风组成的均匀线阵，相邻阵元之间的距离为d。在远场情况下，定义θ(-90°≤θ≤90°)为声源方向与阵列法向之间的夹角。输出信号可表示为

xm(n)=δms[n-τ1m(θ)]+vm(n)

(1)

式中：xm(n),m=1,…,M为麦克风输出信号；δm为传播过程中的衰减因子；s(n)为声源信号；τ1m(θ)=(m-1)dsinθ/c为第m个麦克风和参考麦克风之间的相对时延，其中c为声速，vm(n)为第m个麦克风的加性噪声。在运用LS-SVR估计声源DOA时，首先由模型参数训练出LS-SVR。然后运用LS-SVR模型来估计声源DOA[11]。其中的关键步骤是获取麦克风的观测特征，这里可以将TDOA作为特征来构造LS-SVR。基于LS-SVR的映射方法属于离线工作模式。对于训练角度θk，其TDOA特征向量Γk(k=1,…,N)可表示为

Γk=[τ12，…,τ1M，τ23，…,τ2M，…,τ(M-1)M]T

(2)

式中：τij=(j-i)dsinθ/c为离线条件下第i和第j个麦克风之间的TDOA估计值。通过训练集TDOA，可以由式(3)得到LS-SVR模型的系数α，b，则

(3)

式中：1为全“1”列向量；I为N阶单位矩阵；Ω中元素Ωkl=K(Γk,Γl)，K(·,·)为核函数；α=[α1，…，αN]。文献[12]的研究结果表明径向基核函数的性能较好，其定义为

(4)

式中“‖·‖”为l2范数。在估计声源DOA的过程中，首先通过观测麦克风估计出TDOA的特征向量，则

(5)

(6)

2 基于多核LS-SVR的TDOA-DOA映射方法及其稀疏化分析

针对声源DOA估计中的TDOA-DOA映射问题，本文提出了基于中值滤波的时延离群值消除方法以及基于聚类方法的多核LS-SVR映射方法，并在此基础上对多核LS-SVR映射方法进行稀疏化分析。

2．1 基于中值滤波的TDOA估计离群值处理

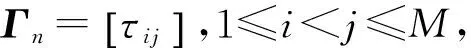
(7)

(8)

图1 仿真实验麦克风阵列的配置图Fig.1 Configuration of microphone array in simulation room

‴n·εn=1,…，N

(9)

通过仿真实验对该方法的性能进行了验证。这里选用尺寸为5 m×4 m×3 m的矩形混响房间。麦克风阵列为四元均匀直线阵列，阵元间距为4 cm，阵列离地高度为0.5 m，声源与麦克风阵列中心的距离为2 m，如图1所示。设定SNR=20 dB，RT60=210 ms时，RT60为混响时间，运用GCC-PHAT方法估计TDOA，在未采用中值滤波方式及采用中值滤波方式处理TDOA的两种情况下，分别采用最小二乘法、LS-SVR这两种映射方法，以50次蒙特卡洛实验的均方根误差为评价指标，仿真结果如图2所示。

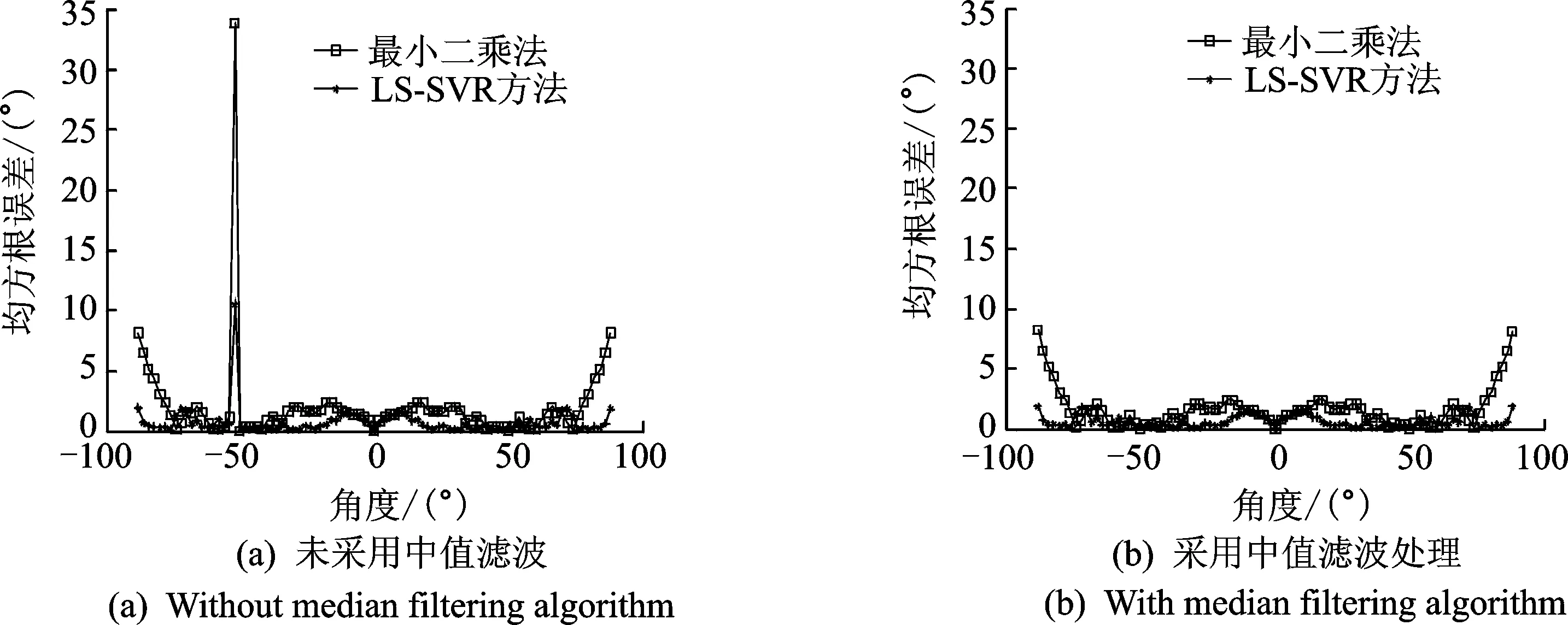
图2 采用中值滤波处理前后，最小二乘法与LS-SVR方法的性能对比Fig.2 Performance comparison of least squares method and LS-SVR method with or without median filtering algorithm

由图2(a)可知，受混响噪声影响，声源的入射角度在-50°附近出现了较大的估计误差。这是由于TDOA估计的精度较差，导致映射DOA时出现了较大误差，从而出现了估计结果不稳定的情况。尤其是采用最小二乘法时，最大均方根误差已超过30°。虽然此时LS-SVR方法要优于最小二乘法，但由于离群值的出现，该方法也出现了较大的估计误差。而在图2(b)中，最小二乘法以及LS-SVR方法的映射性能都没有很大起伏。对比图2(a)与图2(b)可知，在相同的仿真条件下，采用中值滤波方式处理TDOA可有效消除TDOA中的离群值，提高TDOA-DOA映射性能的鲁棒性。

2.2 聚类多核LS-SVR映射方法

核方法虽然能在一定程度上解决非线性模式分析问题，但当样本特征含有异构信息、样本规模很大且数据在高维空间中分布不平坦时，采用单个核函数进行直接映射往往不能达到实际的应用需求，因此出现了很多核组合方法的研究。多核学习方法是一类性能更好的基于核的学习模型，采用多核学习方法可以提升映射性能。在声源DOA估计中，由于声源信号受到混响和噪声的影响，估计时延准确度因环境不同而存在一定差异；而且对于不同的声源DOA，时延估计的准确度也有一定区别。这时采用单核LS-SVR不能很好地对TDOA进行拟合，因此可以将多核方法应用到声源DOA估计中，以提高估计精度。多核(Multiple kernel, MK)学习方法的核心思想就是将R个核函数进行凸组合。只要满足Mercer条件，组合之后的函数就可看作是一种核函数[17]。如

(10)

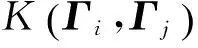
(11)

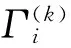
(12)

聚类过程就是寻找最佳聚类中心ck，使目标函数J为最小值，这时聚类中心为

(13)

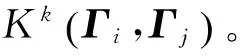
(14)

与最小二乘映射方法相比，对于任意结构的阵列，LS-SVR方法总存在闭式解，因而无需进行搜索求解，从而减小了计算量。仿真实验结果表明，与单核LS-SVR方法相比，多核LS-SVR方法进一步提升了声源DOA估计性能。

2.3 稀疏化处理

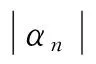
(15)

综上所述，基于稀疏多核LS-SVR的声源DOA估计算法为

步骤1 模型训练

(1) 将声源DOA的分布情况离散化为Θ=[θ1,θ2,…,θN]T。

(2) 对于每一个训练角度，计算出加入理想语音后的TDOA特征向量Γk。

(3) 对纯净语音训练集使用K-Means聚类算法，将其分成Q组并找出Q个聚类中心。

步骤2 剪枝法删减支持向量

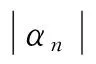
(2) 剔除这些α对应的训练数据，并运用原来的参数组合重新训练，得出新的αk(p)。

(3) 查看DOA估计性能，并重复步骤1(4)-步骤2(2)，直到性能满足要求，或达到预设的循环次数S。

步骤3 DOA估计

(1) 通过麦克风阵列观测数据，构造当前DOA的TDOA特征向量Γ。

(2) 采用中值滤波方法对TDOA进行预处理。

(3) 计算TDOA特征向量Γ与每个聚类中心ck的距离dik，并归入距离最近的一组，记为第k组。

(4) 通过式(15)估计出声源DOA。

3 仿真实验与分析

3.1 聚类多核LS-SVR映射方法仿真实验首先对本文提出的聚类多核LS-SVR映射方法进行仿真。选用矩形混响房间尺寸为5 m×4 m×3 m。麦克风阵列为四元均匀直线阵列，阵元间距为4 cm，阵列离地高度为0.5 m，声源与麦克风阵列中心的距离为2 m，其示意图如图1所示。

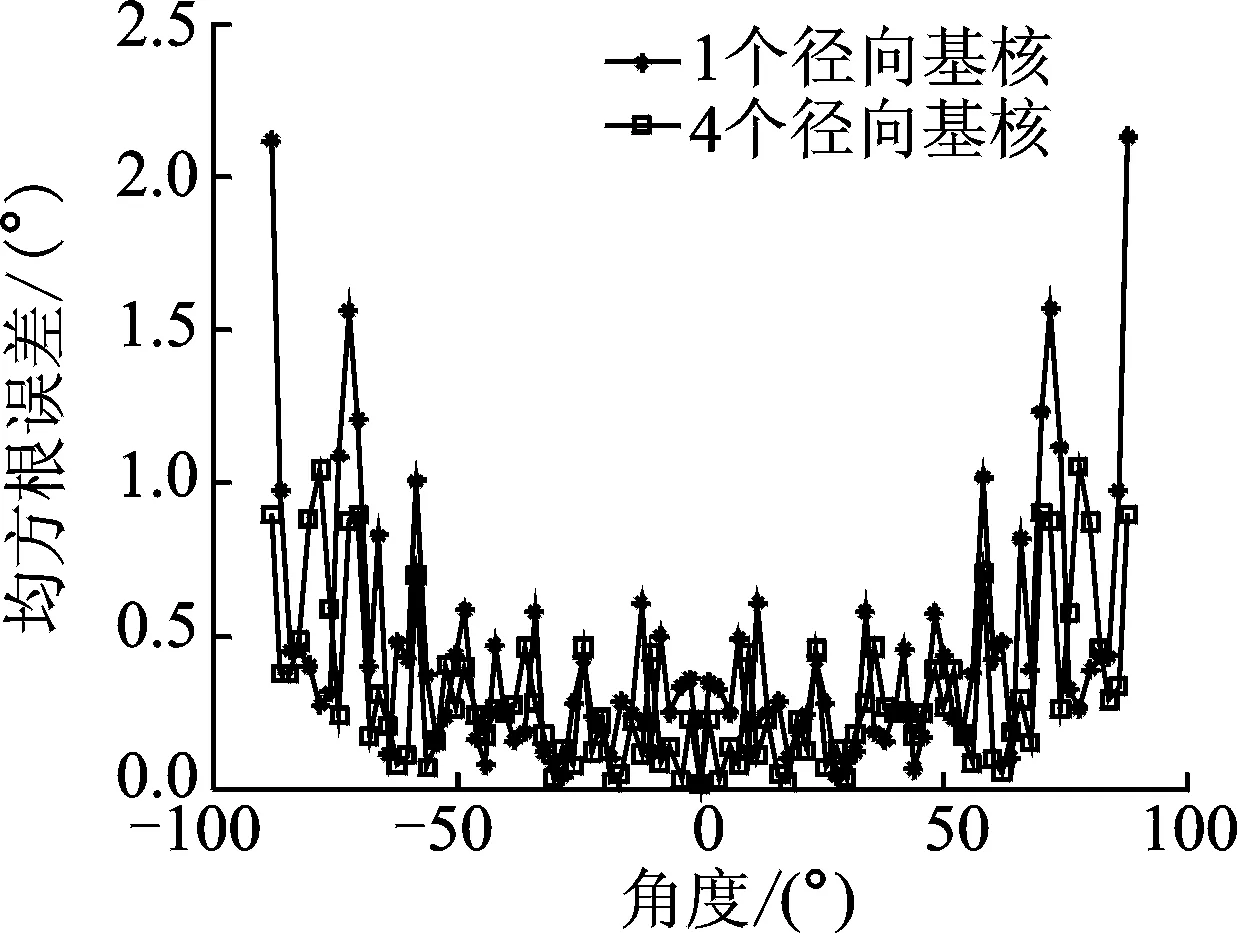
图3 单核与四核LS-SVR的性能比较Fig.3 Performance comparison of single-kernel LS-SVR and quad-kernel LS-SVR

3.1.1 单核与多核映射方法的性能比较(SNR=20 dB，RT60=120 ms)

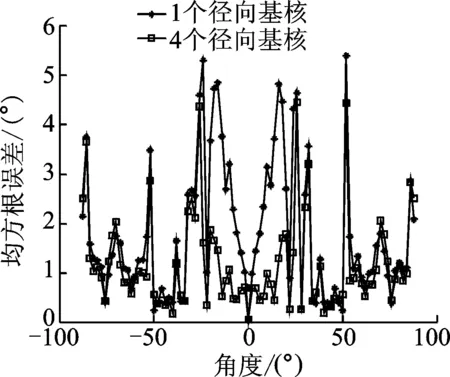
图4 消除离群值后，单核与四核LS-SVR的性能比较Fig.4 Performance comparison of single-kernel LS-SVR and quad-kernel LS-SVR after outlier detection

设定以测试角度为横坐标，50次蒙特卡洛实验后每个角度所对应的均方根误差为纵坐标。运用GCC-PHAT方法获取TDOA，以径向基核为核函数比较采用由1个和4个核函数构造的LS-SVR映射DOA时的性能，如图3所示。在此仿真实验条件下，由于混响和噪声对信号干扰较小，估计出的TDOA准确度较高。由图3可以看出，无论是最大均方根误差还是整体表现，由4个径向基核构造的多核LS-SVR的性能都明显优于单核LS-SVR，尤其是在端射方向；并且由4个径向基核构造的LS-SVR映射得到的角度基本可以控制在1°以内，性能较为稳定，而单核构造的LS-SVR得到的角度起伏较大。

3.1.2 单核与多核映射方法的性能比较(SNR=10 dB，RT60=300 ms)

这里考虑降低信噪比，增大混响时间。以测试角度为横坐标，50次蒙特卡洛实验后每个角度所对应的均方根误差为纵坐标。运用GCC-PHAT方法获取TDOA，采用中值滤波的方法消除离群值，比较采用由1个和4个径向基核构造的LS-SVR映射DOA时的性能，如图4所示。在此仿真条件下，信号受混响影响较大，估计出的TDOA准确度下降。因而采用本文提出的中值滤波方法对TDOA进行处理，有效消除离群值，使得TDOA准确度得到一定提升。从图4可以看出，由4个径向基核构造LS-SVR时的性能在整体上优于由单核构造LS-SVR时的性能。由4个径向基核构造的LS-SVR的最大均方根误差也小于单核LS-SVR。单核LS-SVR在优化参数过程中考虑的是最小化全局损失量，此时的单核LS-SVR更加侧重边界性能，即认为声源入射方向与阵列法向夹角较大时的误差小，整体误差就小，所以图4中单核LS-SVR的边界性能与四核LS-SVR的边界性能相当。四核LS-SVR的特点是可以分区段优化参数，不同核函数针对的角度区域不同，所以在声源入射方向与阵列法向夹角较小时，四核LS_SVR的性能明显优于单核LS-SVR，改善程度可达2°～3°。

3.1.3 不同混响条件下单核与多核映射方法的性能比较

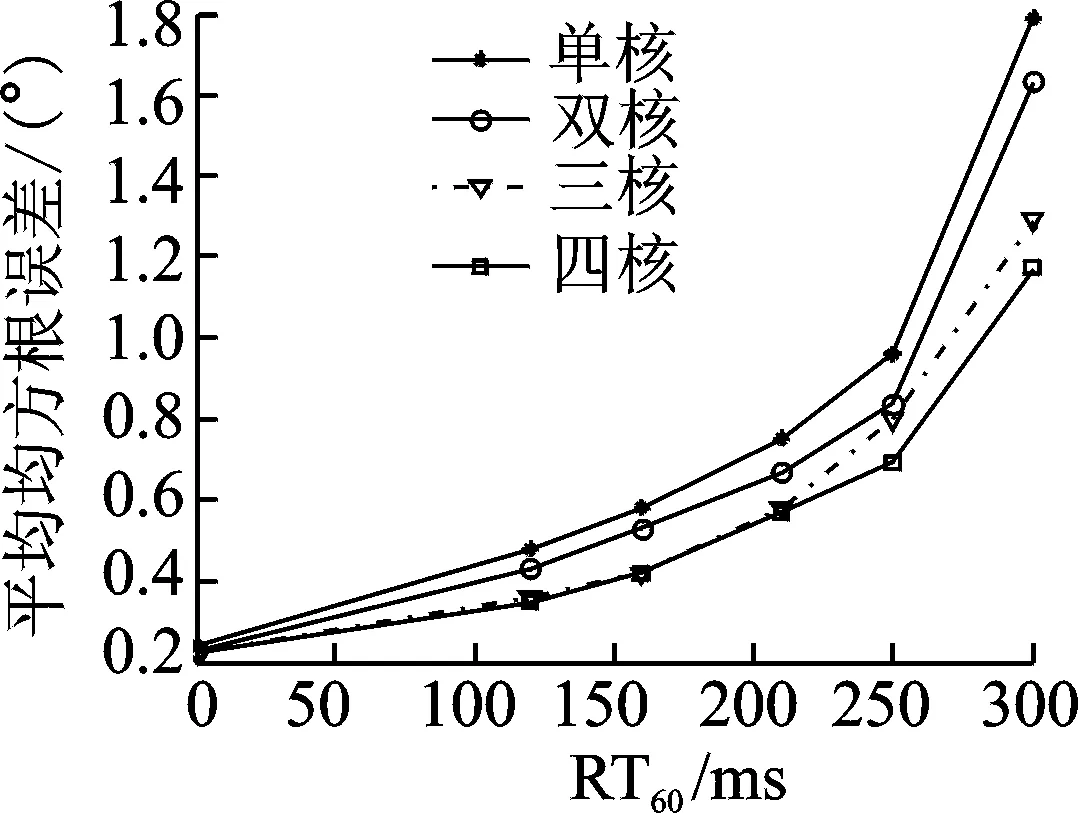
图5 由不同个数核函数构造的LS-SVR性能随RT60的变化Fig.5 Performance of LS-SVR constructed by different numbers of kernel function versus reverberation time

设定SNR=20 dB，无混响以及RT60分别为120，160，210，250和300 ms时，以测试角度为横坐标，50次蒙特卡洛实验后每个角度所对应的均方根误差为纵坐标，运用GCC-PHAT方法获取TDOA，比较采用由1，2，3，4个径向基核构造的LS-SVR映射DOA时的性能，如图5所示。由于DOA估计的精度受混响影响较大，因而本文针对混响对多核LS-SVR的性能作了进一步的分析。对于图5，在整体上，无论由单核还是多核构造的LS-SVR，其平均均方根误差总是随着RT60的增大而增加；在同一仿真条件下，即具有相同SNR和RT60时，由多核构造的LS-SVR性能总是优于单核LS-SVR，且随着核函数数目的增多而进一步提升。

3.1.4 不同环境条件下各映射方法性能的综合比较

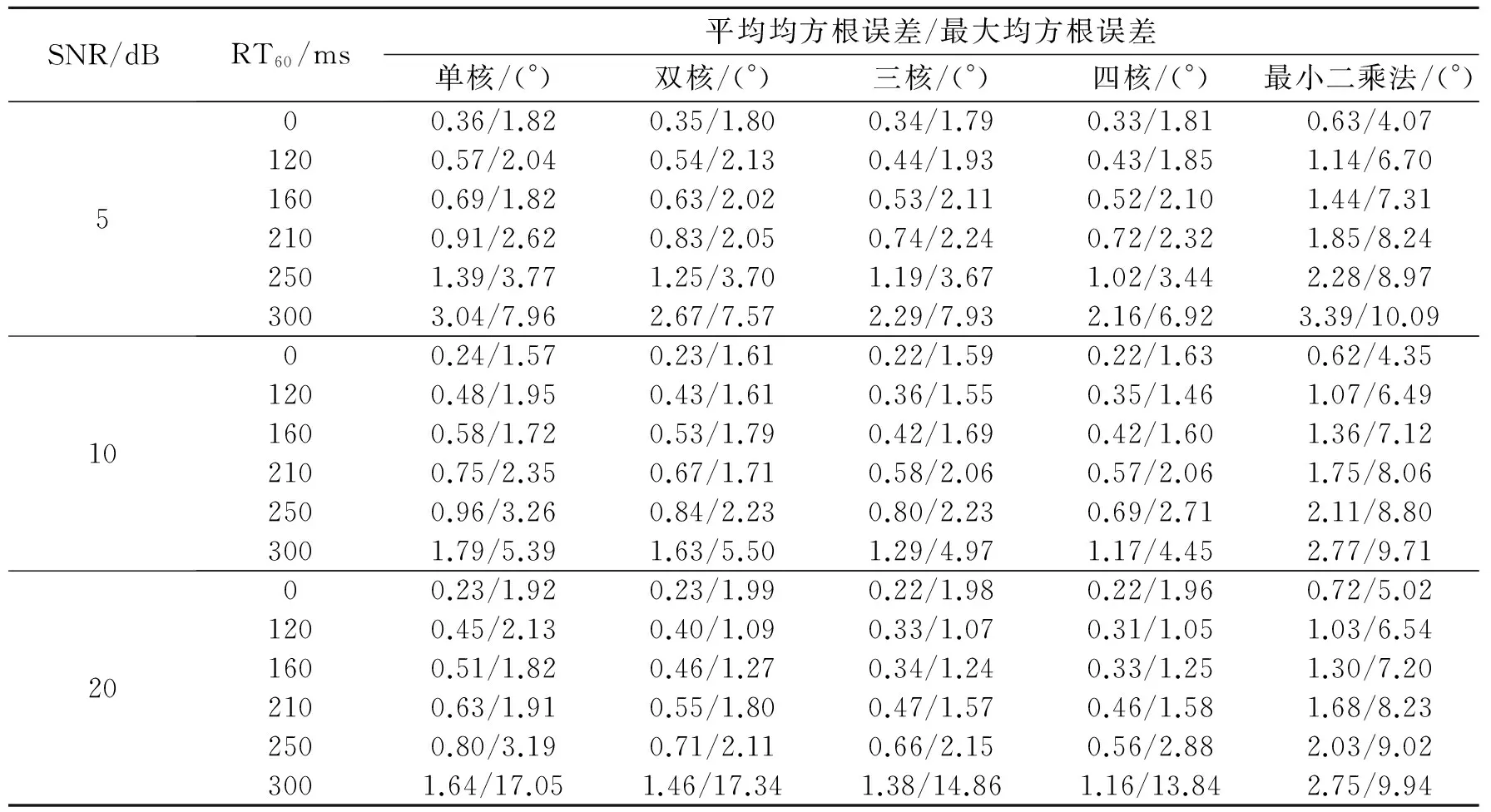
分别设定SNR为5，10和20 dB，无混响以及RT60分别为120，160，210，250和300 ms时，以50次蒙特卡洛实验后所有角度对应的平均均方根误差和最大均方根误差为评价指标，运用GCC-PHAT方法获取TDOA，然后采用中值滤波的方法消除离群值，采用最小二乘法和由1，2，3，4个径向基核构造的LS-SVR进行DOA映射，其性能比较如表1所示。

表1 不同SNR以及不同RT60时，单核LS-SVR、多核LS-SVR与最小二乘法的性能比较

Tab.1 Performance comparison of single-kernel LS-SVR, multi-kernel LS-SVR and least squares method versus different SNR and reverberation time

SNR/dBRT60/ms平均均方根误差/最大均方根误差单核/(°)双核/(°)三核/(°)四核/(°)最小二乘法/(°)500.36/1.820.35/1.800.34/1.790.33/1.810.63/4.071200.57/2.040.54/2.130.44/1.930.43/1.851.14/6.701600.69/1.820.63/2.020.53/2.110.52/2.101.44/7.312100.91/2.620.83/2.050.74/2.240.72/2.321.85/8.242501.39/3.771.25/3.701.19/3.671.02/3.442.28/8.973003.04/7.962.67/7.572.29/7.932.16/6.923.39/10.091000.24/1.570.23/1.610.22/1.590.22/1.630.62/4.351200.48/1.950.43/1.610.36/1.550.35/1.461.07/6.491600.58/1.720.53/1.790.42/1.690.42/1.601.36/7.122100.75/2.350.67/1.710.58/2.060.57/2.061.75/8.062500.96/3.260.84/2.230.80/2.230.69/2.712.11/8.803001.79/5.391.63/5.501.29/4.971.17/4.452.77/9.712000.23/1.920.23/1.990.22/1.980.22/1.960.72/5.021200.45/2.130.40/1.090.33/1.070.31/1.051.03/6.541600.51/1.820.46/1.270.34/1.240.33/1.251.30/7.202100.63/1.910.55/1.800.47/1.570.46/1.581.68/8.232500.80/3.190.71/2.110.66/2.150.56/2.882.03/9.023001.64/17.051.46/17.341.38/14.861.16/13.842.75/9.94

为全面展示各种混响噪声条件下不同映射方法的性能，表1给出了各种仿真条件下，多核构造的LS-SVR、单核LS-SVR以及最小二乘法的映射性能。在总体上，随着SNR的下降以及RT60的增大，各种映射方法的平均均方根误差和最大均方根误差都增大，即性能都变差。在SNR和RT60相同时，多核LS-SVR的性能要优于单核LS-SVR以及最小二乘法；一般情况下，核的个数越多，多核LS-SVR的性能越好；且混响时间越大，多核LS-SVR映射方法的性能优势越明显。

3.2 稀疏化分析仿真实验

对本文提出的基于稀疏多核LS-SVR的声源DOA估计算法进行了仿真验证，在指定SNR和RT60下，采用中值滤波方法处理TDOA，给出了该方法随稀疏次数的性能变化情况；并与未稀疏的多核LS-SVR、未稀疏的单核LS-SVR和稀疏单核LS-SVR等映射方法进行了比较。

3.2.1 稀疏多核与未稀疏多核映射方法的性能比较

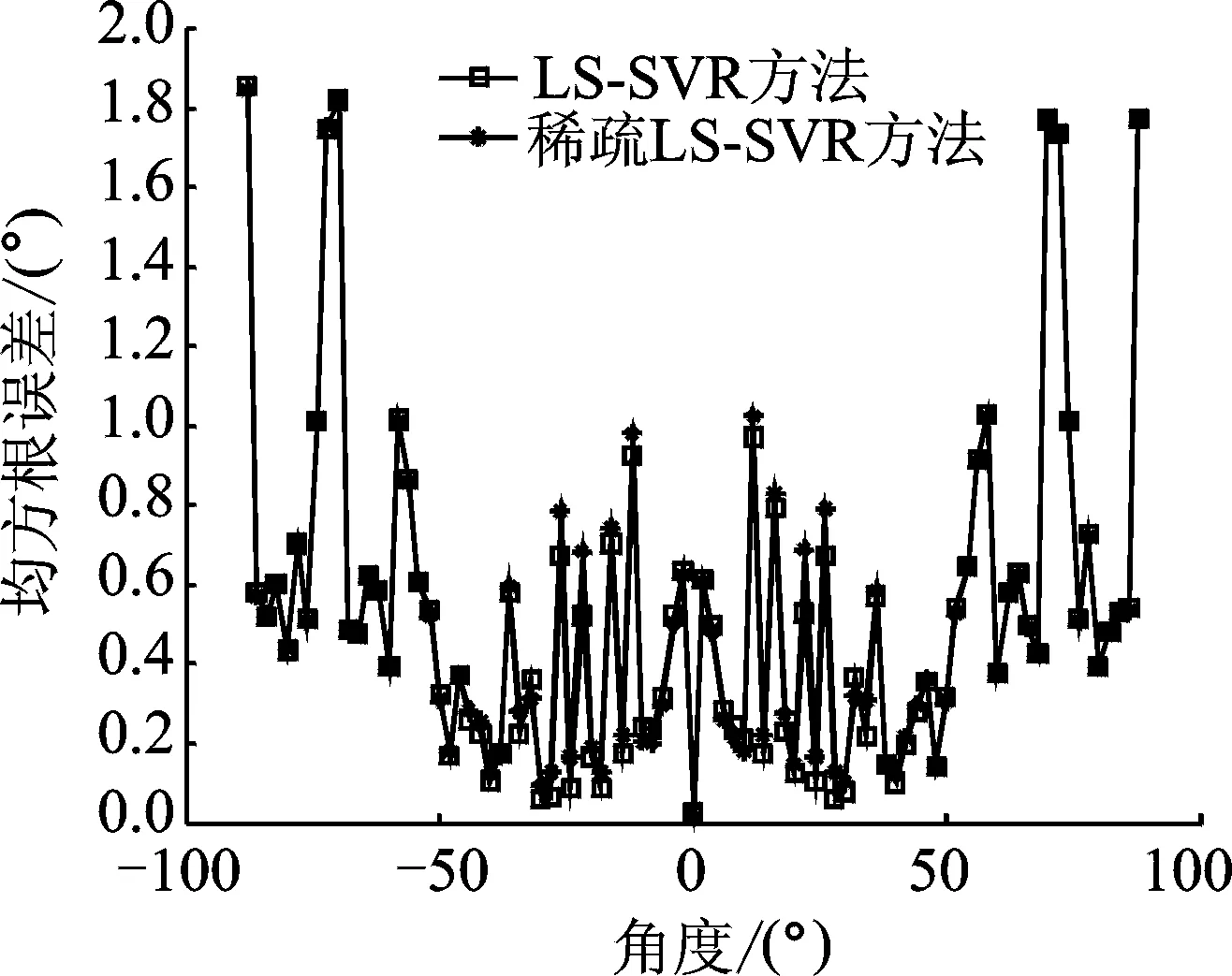
图6 稀疏8次多核LS-SVR方法与未稀疏方法的性能比较Fig.6 Performance comparison of multi-kernel LS-SVR after eight-time sparsification and without sparsification

设定SNR=20 dB，RT60=250 ms时，运用GCC-PHAT方法获取TDOA，使用中值滤波方法处理TDOA，以测试角度为横坐标，50次蒙特卡洛实验后每个角度所对应的均方根误差为纵坐标，采用4个径向基核构造LS-SVR，然后比较未稀疏与稀疏8次时的多核LS-SVR性能，如图6所示。由图6可知，稀疏8次后的多核LS-SVR性能与未稀疏的多核LS-SVR性能十分接近，都能保持较高的准确度；尤其是在端射方向附近，这两种方法的性能几乎一致。虽然在DOA较小时，稀疏8次后的多核LS-SVR方法与未稀疏的多核LS-SVR的性能相比存在一定差异，但两者之间的差异几乎可以忽略。所以稀疏多核LS-SVR在降低运算量的情况下仍能保持较好的映射性能。

3.2.2 稀疏次数对稀疏多核映射方法性能的影响

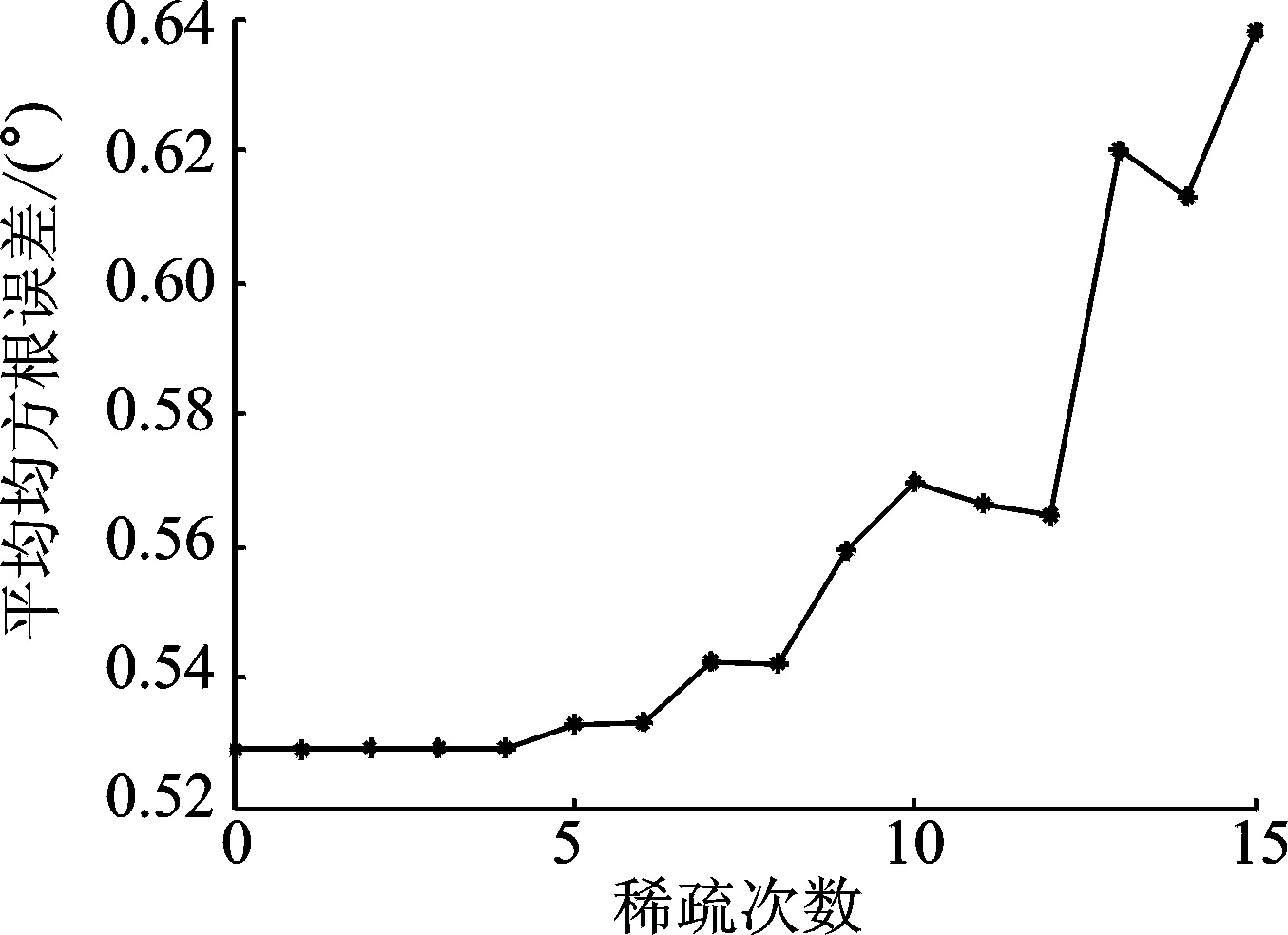
图7 多核LS-SVR方法的性能随稀疏次数变化趋势Fig.7 Performance of multi-kernel LS-SVR method versus time of sparsification

设定SNR=20 dB，RT60=250 ms，运用GCC-PHAT方法获取TDOA，使用中值滤波方法处理TDOA，再采用四核LS-SVR映射DOA，以50次蒙特卡洛实验的所有DOA的平均均方根误差为评价指标，稀疏LS-SVR方法的平均均方根误差随稀疏次数的变化情况如图7所示。由图7可知，随着稀疏次数的增多，平均均方根误差缓慢增大，尤其是稀疏次数在5次以内时，性能几乎保持一致。即便稀疏到10次时，平均均方根误差只增加了0.05。当稀疏次数增大到15次时，平均均方根误差增加了0.11。这是由于在一定范围内数据量减小时，只是剔除了一部分冗余的支持向量，对测试效果几乎无影响。而当数据量减小到一定程度时，由于训练阶段对映射曲线的学习不够全面，因而对于部分测试数据没有达到理想的映射效果，因此不能无限地进行稀疏。

3.2.3 单核和多核映射方法随稀疏次数的性能变化

设定SNR=20 dB，RT60=250 ms，运用GCC-PHAT方法获取TDOA，使用中值滤波方法处理TDOA，采用由单核、双核、三核以及四核构造的LS-SVR映射DOA，并在此基础上分别进行稀疏化，以50次蒙特卡洛实验的所有DOA的平均均方根误差和最大均方根误差为评价指标。表2呈现了不同个数的核函数构造的LS-SVR在不同稀疏次数下的性能。稀疏之前训练集的样本数目为89，由于每次剔除当前训练集中的5%的数据，因而1次稀疏后支持向量比例为原支持向量集合的95.5%。稀疏5次，10次和15次后支持向量比例分别为原支持向量集合的79.8%，64%和52.8%。由表2可知，一般情况下，在指定核函数个数时，随着稀疏次数增多，无论由多少个核构造LS-SVR，其性能总是随着稀疏次数缓慢变化。当稀疏次数增大到一定数目时，其估计性能可能会急剧恶化，如表2中单核和三核构造的LS-SVR。但在稀疏10次以内时，各种LS-SVR方法都能保持稳定的性能，即至少可以剔除36%的冗余向量，且在指定稀疏次数时，随着核的个数增多，多核LS-SVR的性能也得到提升，例如与单核LS-SVR相比，四核LS-SVR的平均均方根误差减少了0.28°左右，最大均方根误差减少了1.4°左右。同时，在稀疏15次时，即剔除47.2%的冗余向量时，四核LS-SVR仍能保持很好的DOA估计性能。总而言之，稀疏多核LS-SVR方法在保持优越的DOA估计性能的同时，有效减小了测试时的运算量。

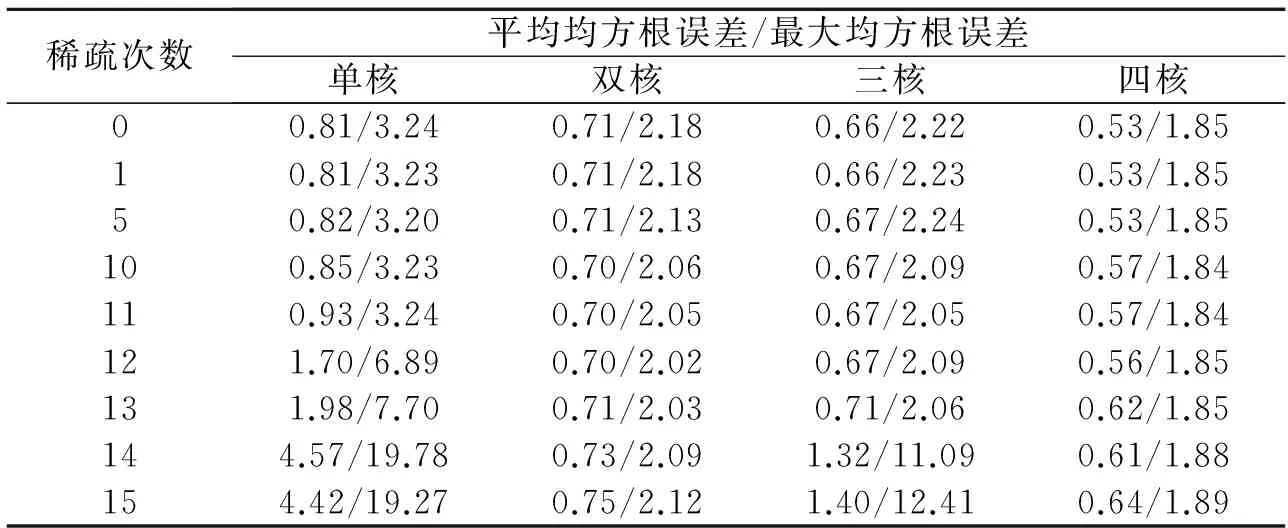
表2 不同数目核构造的LS-SVR，性能随稀疏次数的变化

4 结束语

本文针对声源DOA估计中的TDOA-DOA映射问题，提出了基于聚类方法的多核LS-SVR映射方法，在此基础上对多核LS-SVR映射方法进行稀疏化分析。仿真结果表明，该映射方法的性能要优于现有的单核LS-SVR以及最小二乘法。一般情况下，随着核个数增多，多核LS-SVR的性能也更好。混响时间较大时，多核LS-SVR映射法的性能优势体现得更明显。由于多核LS-SVR映射方法运用的LS-SVR中，所有训练集都为支持向量，缺乏稀疏性，使得测试时运算量较大。因而对于基于LS-SVR的TDOA-DOA映射中的多核函数方法，有必要通过稀疏化消除TDOA集合中存在的冗余。仿真结果表明，与基本的多核LS-SVR相比，稀疏多核LS-SVR映射方法不仅能保持良好的DOA估计性能，而且有效减小了测试时的运算量。

[1] Zhang C, Florencio D, Ba D E, et al. Maximum likelihood sound source localization and beamforming for directional microphone arrays in distributed meetings[J]. IEEE Transactions on Multimedia, 2008, 10(3): 538-548.

[2] 李晓飞, 刘宏.机器人听觉声源定位研究综述[J]. 智能系统学报, 2012,7(1):9-20.

Li Xiaofei, Liu Hong. A survey of sound source localization for robot audition[J]. CAAI Transactions on Intelligent Systems, 2012, 7(1): 9-20.

[3] 栗志意,张卫强, 何亮,等. 基于核函数的IVEC-SVM说话人识别系统研究[J].自动化学报, 2014,40(4):780-784.

Li Zhiyi, Zhang Weiqiang, He Liang, et al. Speaker recognition with kernel based IVEC-SVM[J]. ACTA Automatica Sinica,2014,40(4):780-784.

[4] Hahn W R, Tretter S A. Optimum processing for delay-vector estimation in passive signal arrays [J].IEEE Transactions on Information Theory,1973,19(5):608-614.

[5] 谭颖,殷福亮,李细林.改进的SRP-PHAT声源定位方法[J].电子与信息学报,2006,28(7):1223-1227.

Tan Ying, Yin Fuliang, Li Xilin.Sound localization method using modified SRP-PHAT algorithm[J]. Journal of Electronics & Information Technology, 2006, 28(7): 1223-1227.

[6] Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation, 1986,34(3):276-280.

[7] Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1990, 37(7): 984-995.

[8] 何赛娟, 陈华伟, 尹明婕,等.基于差分麦克风阵列和语音稀疏性的多源方位估计方法[J]. 数据采集与处理,2015,30(2):372-381.

He Saijuan, Chen Huawei, Yin Mingjie, et al. Direction finding of multiple sound sources based on sparseness of speech signals and differential microphone array[J]. Journal of Data Acquisition and Processing, 2015,30(2):372-381.

[9] 郭业才, 宋宫琨琨, 吴礼福,等.基于圆形麦克风阵列的声源定位改进算法[J]. 数据采集与处理, 2015,30(2):344-349.

Guo Yecai, Song Gong Kunkun, Wu Lifu, et al. Improved algorithm of sound source localization using circular microphone array[J]. Journal of Data Acquisition and Processing, 2015,30(2):344-349.

[10] Huang Y, Benesty J, Chen J. Acoustic MIMO signal processing [M]. Berlin: Springer, 2006.

[11] Chen H, Ser W. Sound source DOA estimation and localization in noisy reverberant environments using least-squares support vector machines[J]. Journal of Signal Processing Systems, 2011, 63(3):287-300.

[12] 张峰, 陈华伟, 王天南,等.声源DOA估计中LS-SVR核函数选取研究[J]. 电声技术, 2014,38(5): 57-61.

Zhang Feng, Chen Huawei, Wang Tiannan, et al. Selection research of LS-SVR kernels for sound source DOA estimation[J]. Audio Engineering,2014,38(5):57-61.

[13] 汪洪桥, 孙富春, 蔡艳宁,等.多核学习方法[J]. 自动化学报, 2010,36(8):1037-1050.

Wang Hongqiao, Sun Fuchun, Cai Yanning, et al. On multiple kernel learning methods[J]．ACTA Automatica Sinica, 2010,36(8):1037-1050.

[14] Knapp C, Carter G. The generalized correlation method for estimation of time delay [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1976, 24(4): 320-327.

[15] 梁宇, 马良, 纳霞等.基于广义互相关算法的时延估计[J].计算机科学, 2011,38(B10):454-456.

Liang Yu, Ma Liang, Na Xia, et al. Research of time delay estimation based on GCC algorithm[J]. Computer Science, 2011, 38(B10): 454-456.

[16] Hong Y, Kwong S, Wang H. Decision-based median filter using k-nearest noise-free pixels[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Taiwan， China: ICASSP, 2009: 1193-1196.

[17] 赵犁丰, 李新, 王栋.多核模糊聚类算法的研究[J]. 中国海洋大学学报: 自然科学版, 2009,39(5): 1047-1050.

Zhao Lifeng, Li Xin, Wang Dong. Clustering algorithm based on multiple kernel SVM[J]. Periodical of Ocean University of China,2009,39(5): 1047-1050.

[18] Cortes C, Mohri M, Rostamizadeh A. Learning non-linear combinations of kernels[J]. Advances in Neural Information Processing Systems,2009,22:396-404.

[19] Wang Z, Jie W, Gao D. A novel multiple Nystrom-approximating kernel discriminant analysis[J]. Neurocomputing, 2013, 119: 385-398.

[20] 贺玲, 吴玲达, 蔡益朝.数据挖掘中的聚类算法综述[J].计算机应用研究,2007,24(1):10-13.

He Ling, Wu Lingda, Cai Yichao. Survey of clustering algorithms in data mining[J]. Application Research of Computers,2007,24(1):10-13.

[21] 梁烨炜.K-均值聚类算法的改进及其应用[D].长沙: 湖南大学, 2012:20-24.

Liang Yewei.Improvent of K-means clustering algorithm and its application[D].Changsha: Hunan University, 2012:20-24.

[22] Suykens J A K, Lukas L, Vandewalle J. Sparse approximation using least squares support vector machines[C]∥IEEE International Symposium on Circuits and Systems. Geneva: ISCAS, 2000:757-760．

In sound source direction of arrival (DOA) estimation, one of the typical methods is based on the time difference of arrival (TDOA). For the TDOA-based sound source DOA estimation, the TDOA-DOA mapping is a crucial step. Here, we propose a TDOA-DOA mapping approach based on the multi-kernel least-squares support vector regression (LS-SVR), and also analyze its performance with sparsification. In addition, we present an outlier detection method based on the normalized median filtering to post-process the TDOA estimation for improving the performance of TDOA-DOA mapping in noisy reverberant environments. Simulation results show that the proposed method is superior to its counterparts, such as LS and single-kernel LS-SVR methods.

sound source DOA estimation； TDOA estimation； least-squares support vector regression(LS-SVR)； multi-kernel learning

国家自然科学基金(61471190)资助项目。

2014-05-09；

2016-10-14

TN911．7

A

张峰(1989-)，男，硕士研究生，研究方向：音频与语音信号处理，E-mail：zhangfeng@nuaa.edu.cn。

陈华伟(1977-)，男，教授，研究方向：音频与语音信号处理、阵列信号及统计信号处理。

李妍文(1992-)，女，硕士研究生，研究方向：音频与语音信号处理。

TDOA-DOA Mapping Using Multi-kernel Least-Squares Support Vector Regression

Zhang Feng, Chen Huawei, Li Yanwen

(College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China)