基于矩阵法的无节奏流水施工工期优化

魏 凯

(天津铁道职业技术学院，天津 300240)



基于矩阵法的无节奏流水施工工期优化

魏 凯

(天津铁道职业技术学院，天津 300240)

对无节奏流水施工的工期优化问题进行了研究，结合流水施工基本参数和无节奏流水施工的特点，分析了“潘特考夫斯基法”对工期的确定，将矩阵法应用到工期优化中，通过对施工段施工顺序的优化，达到了无节奏流水施工工期优化的效果。

流水施工，工期，矩阵法，施工段

经济发展离不开基础建设，目前，我国建筑市场范围很广，如何在广大的市场中寻求最大的经济效益，一直是工程管理的热点[1]。工程项目管理主要包括“三控三管一协调”[2]，其中进度管理直接关乎施工工期。因此，工期研究是非常必要的。

工程项目在组织施工过程中，施工方式有很多种，本文主要研究流水施工。流水施工可理解为将一个施工项目先分为若干施工对象，再分为若干个施工过程，相应成立施工作业队，保证施工连续进行，不至于出现窝工现象[3]。本文主要研究最接近实际情况的无节奏流水施工，及其施工工期的优化。

1 流水施工的基本参数

流水施工参数用来表达施工状态，主要包括时间参数、空间参数和工艺参数三类，分别对应时间安排、空间布局和工艺流程。针对研究内容，将需要的流水参数做如下介绍。

1.1 时间参数

时间参数包括流水节拍、流水步距、施工工期以及间歇时间和搭接时间。

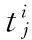
流水步距是指相邻的两个施工过程先后进入第一个施工段的时间间隔。其大小取决于流水节拍及施工组织方式，一般用K表示，Ki,i+1表示第i个和第i+1个施工过程之间的流水步距。

施工工期是指从施工开始，到完成施工所经历的时间，一般用T表示。

间歇时间是指由于不能立即开始施工，必须等待的时间，可分为技术间歇时间和组织间歇时间，一般技术间歇时间用J表示，组织间歇时间用Z表示。

搭接时间是指后一个施工作业队提前进入后一个施工段的时间间隔，一般用D表示。

1.2 空间参数

时间参数主要包括作业面、施工段和施工层。

施工段是指将工程项目划分为的区段，划分是应尽量保证施工量相等，施工段数一般用m表示。

1.3 工艺参数

工艺参数主要包括施工过程和流水强度。施工过程是指每个施工对象再详细划分的子项，一般用n表示。

2 无节奏流水施工及其工期的计算

2.1 节奏流水施工简介

无节奏流水施工是指各施工段上同一施工过程流水节拍可能不相等的组织方式[2]。

2.2 无节奏流水施工流水步距的计算

无节奏流水施工流水步距的计算通常采用“潘特考夫斯基法”，即“累加数位错位相减取大差”法。

“累加数位”：由施工过程在各施工段的流水节拍组成数列，依次累加；

“错位相减”：将上述累加数列错位相减，得到一个差数列；

“取大差”：取差数列中最大值。

2.3 无节奏流水施工工期的计算

无节奏流水施工的工期计算公式为：

T=∑Ki,i+1+Tn+∑J+∑Z-∑D。

其中,Ki,i+1为相邻两个施工过程的流水步距；Tn为最后一个施工过程的持续时间；∑J为技术间歇时间的和；∑Z为组织间歇的和；∑D为搭接时间的和。

3 基于矩阵法无节奏流水施工的工期优化

按照上述的工期计算公式确定无节奏流水施工工期的前提是默认了各施工段的施工排列顺序。本文主要研究通过各施工段施工顺序的确定，从而对施工工期进行优化。本文应用矩阵法解决施工段的排序问题。

矩阵法认为，施工工期的长短主要受间歇时间的影响，即各施工段因为施工顺序不同造成施工过程的间歇时间不同。矩阵法在解决施工段排序问题时引入两个参数，排序间歇时间和排序流水步距。通过施工段的两两组合，计算排序流水步距和排序间歇时间，进而构成排序间歇时间矩阵表；对矩阵表进行研究分析，从而确定各施工段的排列顺序；在施工段排序最优的情况下利用“累加数位错位相减取大差”计算工期。矩阵法简便、易操作，能借助EXCEL等工具进行计算。

1)施工段两两组合进行参数的确定，求得排序流水步距和排序间歇时间；若施工段数为m个，则参数应有m2个。

排序流水步距计算公式为:

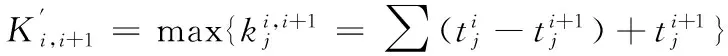
2)构建排序间歇时间矩阵表(m×m)。

3)施工段最优排序的确定：首先，从矩阵表中选择排序间歇时间相对最小的施工段；其次，比较各施工段的持续时间，选择持续时间相对最短的两个施工段，比较这两个施工段第一个施工过程的流水节拍，将流水节拍较小的施工段放在最前面，另一个施工段放在最后面；尽可能将持续时间最长的施工段排在中间；接着，确定其他施工段的排列顺序；最后，选择排序间歇时间最短的排序模型。

4)根据施工段最优排列顺序，利用“累加数位错位相减取大差”计算优化工期。

4 案例分析

某分部工程划分为A,B,C,D四个施工过程，分四个施工段，流水节拍如表1所示，且施工过程B完成后需要有1 d的技术间歇时间，组织无节奏流水施工，进行工期的计算。

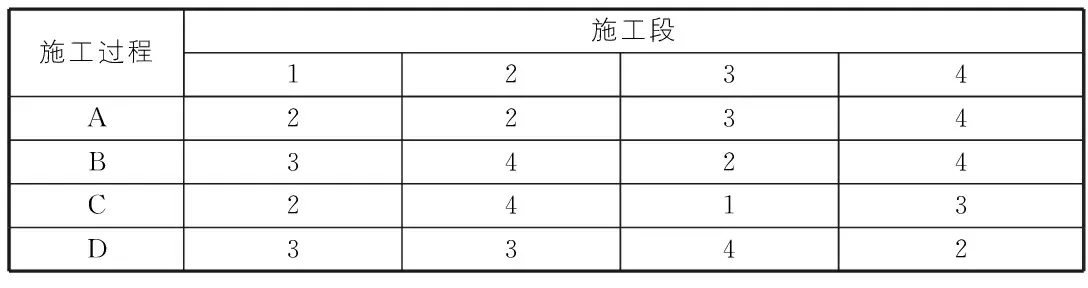
表1 流水节拍表

4.1 直接进行工期的计算

施工过程的顺序是固定不变的，首先按照施工段1-2-3-4的顺序进行施工组织，计算施工工期。

1)由已知条件可得，m=n=4。

2)采用“累加数列错位相减取大差”法计算流水步距。

2, 4, 7, 11

-)3, 7, 9, 13

K1,2=max[2, 1, 0, 2, -13]=2周。

3, 7, 9, 13

-)2, 6, 7, 10

K2,3=max[3, 5, 3, 6, -10]=6周。

2, 6, 7, 10

-)3, 6, 10, 12

K3,4=max[2, 3, 1, 0, -12]=3周。

3)计算流水工期。

T=∑Ki,i+1+Tn+∑J+∑Z-∑D=

(2+6+3)+12+1=24周。

4.2 矩阵法工期的优化

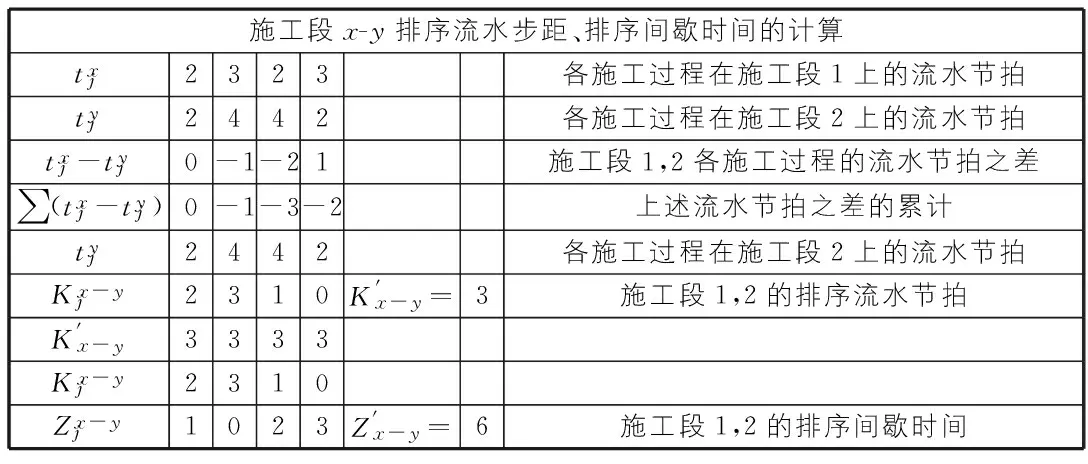
表2 排序流水节拍、排序间歇时间的计算

利用矩阵法进行施工段施工顺序的优化，进而计算优化后的施工工期。

1)排序流水步距和排序间歇时间的确定。

同理，可得：

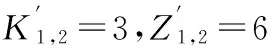
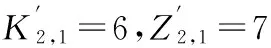
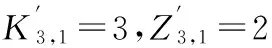
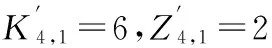
2)构建排序间歇时间矩阵表(见表3)。

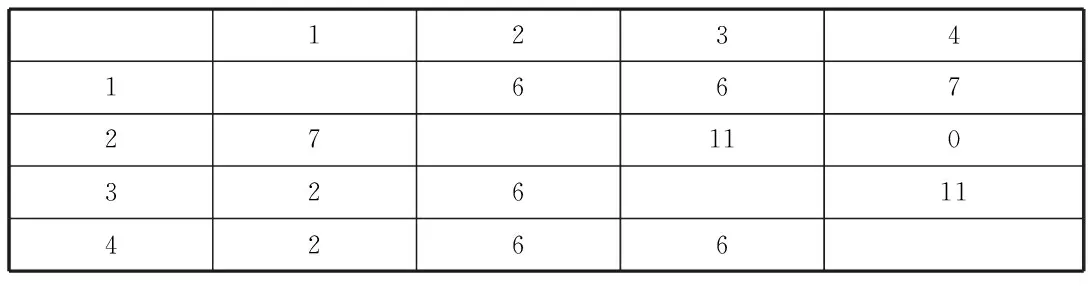
表3 排序间歇时间矩阵表

3)施工段最优排序的确定：由上述规则可得最后排序是1-2-4-3。

4)根据施工段最优排列顺序，利用“累加数位错位相减取大差”计算优化工期。

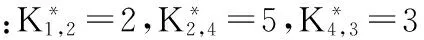
优化工期为：

T=∑Ki,i+1+Tn+∑J+∑Z-∑D=

(2+5+3)+(3+3+4+2)+1=23周。

优化前后对比可得，由于施工段施工顺序的改变，使工期减少了1周。

5 结语

由于流水施工在施工组织中应用非常广泛，无节奏流水施工又最接近项目实际情况，本文针对无节奏流水施工工期问题进行研究，通过矩阵法可以对施工段的施工顺序进行优化，再结合“累加数位错位相减取大差”法，可以进行工期的优化计算。最后结合具体案例，对文章结论进行验证。

[1] 郑显春.异步距异节奏流水施工组织方法研究[J].施工技术，2013(10):105-107.

[2] 李鹏飞.公路施工组织设计与管理[M].北京：北京邮电大学出版社，2016.

[3] 郑显春.土木工程施工组织[M].北京：中国建材工业出版社，2009.

[4] 魏道升.论异节拍流水施工中流水工期差异的实质[J].重庆交通大学学报(自然科学版)，2013(3):42-45.

[5] 李会静.基于间歇时间和流水步距的流水施工优化模型[J].科技通报,2016(2):119-122.

Optimize the construction period of non-rhythm flow process based on matrix method

Wei Kai

(TianjinRailwayTechnicalandVocationalCollege,Tianjin300240,China)

This paper researched the optimization of the construction period of non-rhythm flow process. This paper firstly analyzed the construction period by paterkovsky method combined with basic parameters of flow process and characterisitics of non-rhythm flow process. Then optimized the construction period of non-rhythm flow process based on matrix method.

flow process, construction period, matrix method, construction section

1009-6825(2017)17-0097-02

2017-03-21

魏 凯(1988- )，男，助教

TU745

A