剖析立体几何中几个常见模型的运用
浙江省宁波市第四中学 (邮编:315016)
剖析立体几何中几个常见模型的运用
浙江省宁波市第四中学张延斌魏定波(邮编:315016)
教育部《普通高中数学课程标准》修订组组长、博士生导师王尚志教授在“关于普通高中数学课程标准修订”的专题报告中,他提出中国学生在数学学习中应培养好六大数学核心素养,即数学抽象、逻辑推理、数学建模、运算能力、直观想象、数据分析.相比之下,当前无论是课程的编制、教学计划的制订,还是教学效果的评估,数学建模是最为薄弱的一项.由此看来,如何提供一些基本内容的实际背景,反映数学的应用价值,开展“数学建模“活动,将成为我们数学课堂教学的重要方法和手段.下面就立体几何中几个常见模型运用给以举例说明.
1长方体模型例1 (2016年北京市高考数学试卷第6题)某三棱锥的三视图如图1-1所示,则该三棱锥的体积为( )
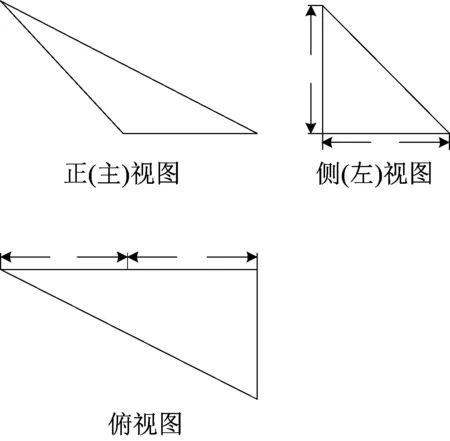
图1-1
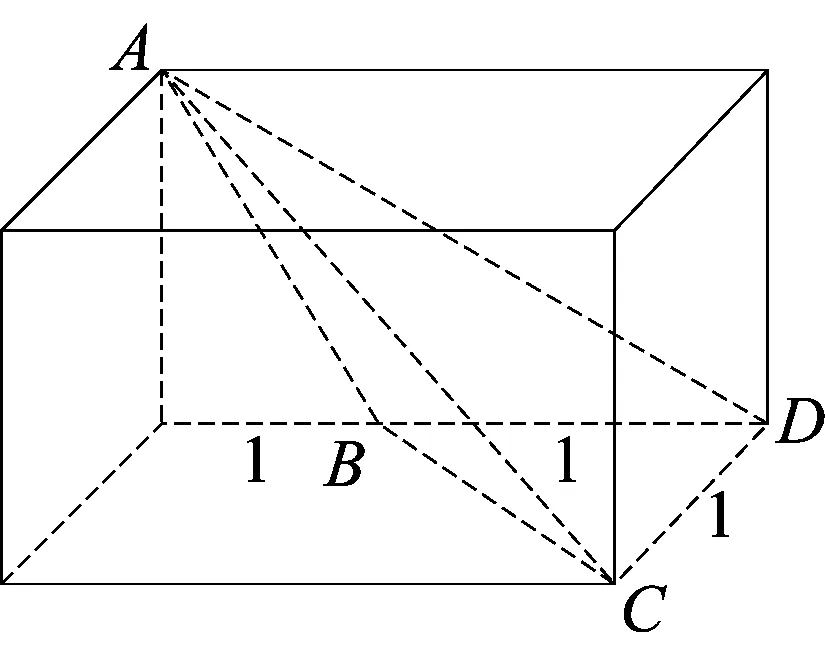
图1-2
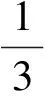
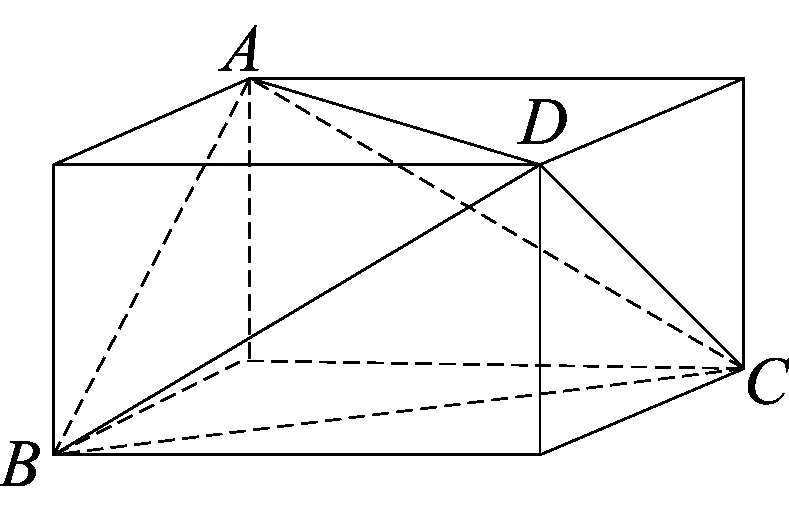
图2
例2 (2010年河北省高中数学竞赛试题)在四面体ABCD中,三组对棱分别相等,依次为了5、4、x,则x的取值范围为( )
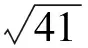
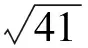
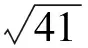
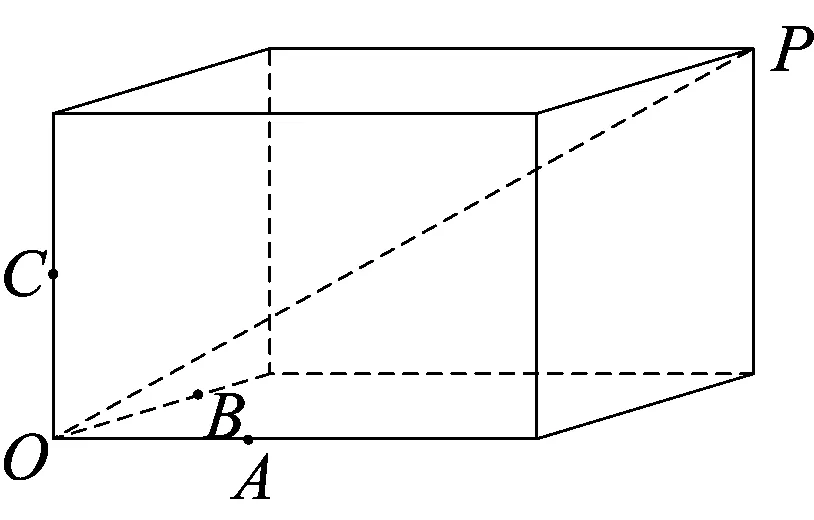
图3
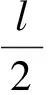
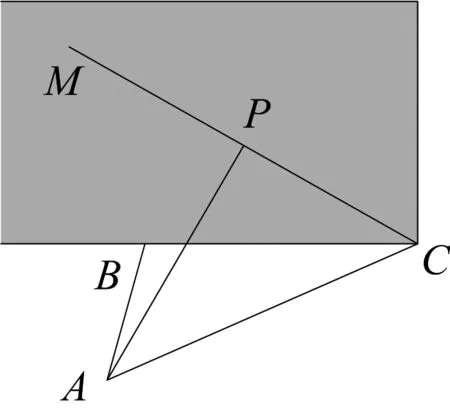
图4-1

图4-2
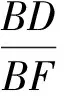
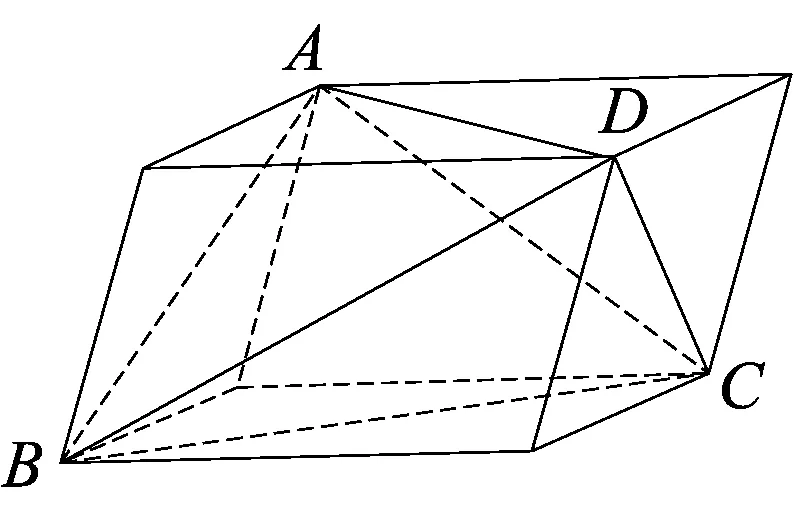
图5
例5 (第十一届“希望杯”全国数学邀请赛高一试题)已知四面体ABCD中,AB2+CD2=BC2+AD2,则异面直线AC、BD所成角的度数是( )
A.90° B.60° C.45° D.30°
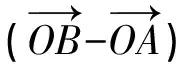
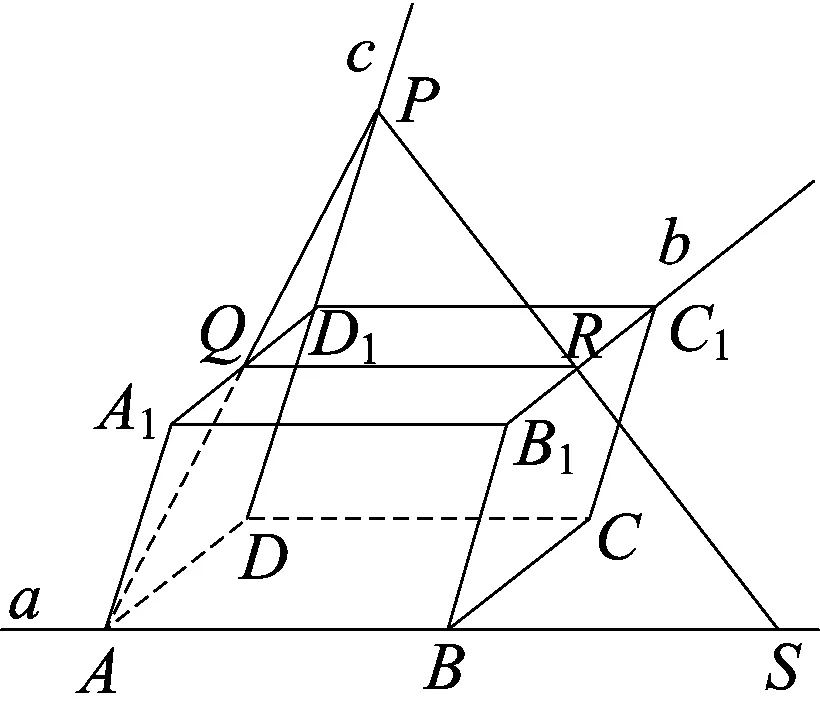
图6
例6 (2008年辽宁省高考试题改编)如果空间三条直线a、b、c两两成异面直线,那么与a、b、c都相交的直线有( )
A.不存在B.有且只有两条
C.有且只有三条D.有无数条
解析在a、b、c上取三条线段AB、B1C1、DD1,作一个平行六面体ABCD-A1B1C1D1,如图6所示在c上,即在直线DD1上取一点P,过a、P作一个平面β,平面β与A1D1交于Q、与C1D1交于R,则由面面平行的性质定理,得QR∥a,于是PR不与a平行,但PR与a共面.故PR与a相交,得直线PR是与a、b、c都相交的一条直线,根据点P的任意性,得与a、b、c都相交的直线有无穷多条.故选D.
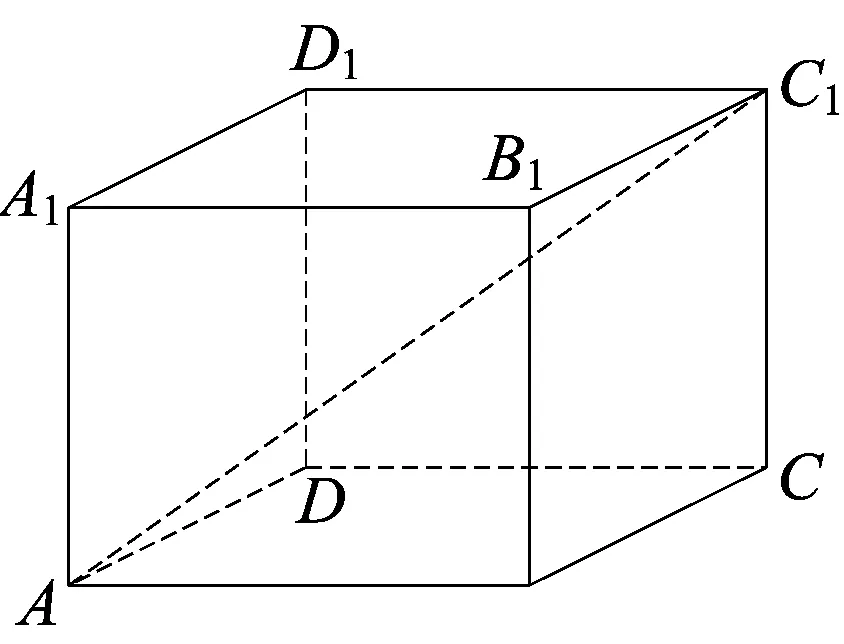
图7-1
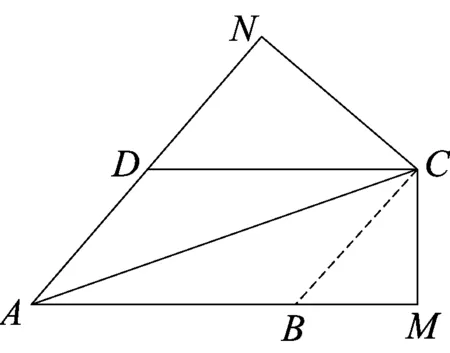
图7-2

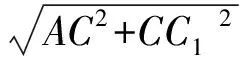
评注由空间向量建立的平行六面体,与四面体具有密切的“母子相依”关系,涉及四面体的问题(如异面直线的夹角、三棱椎的体积等),可把四面体放置到平行六面体中,以扩大解题活动的空间,构造恰到好处的参照物,从而妙解相关问题.3圆锥模型
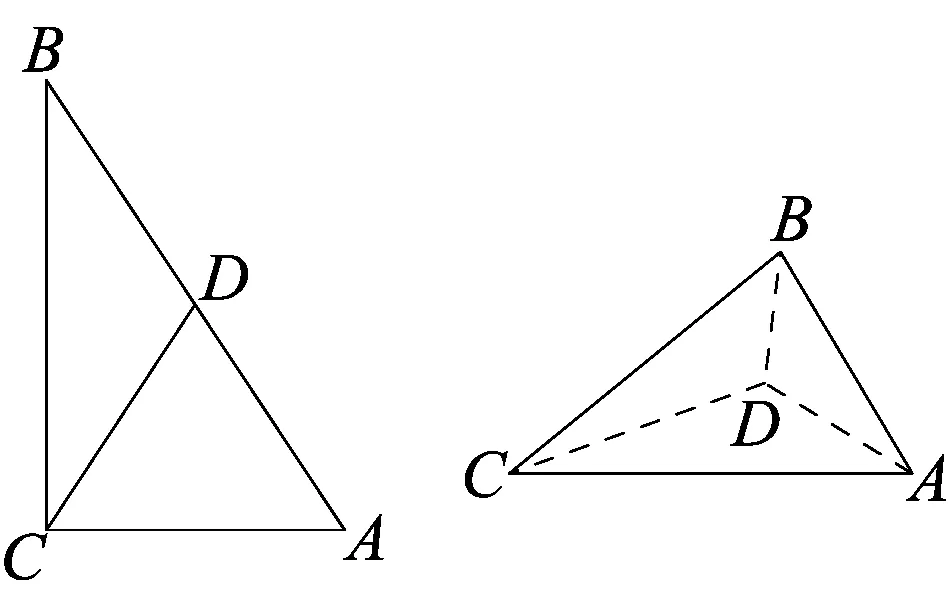
图8-1
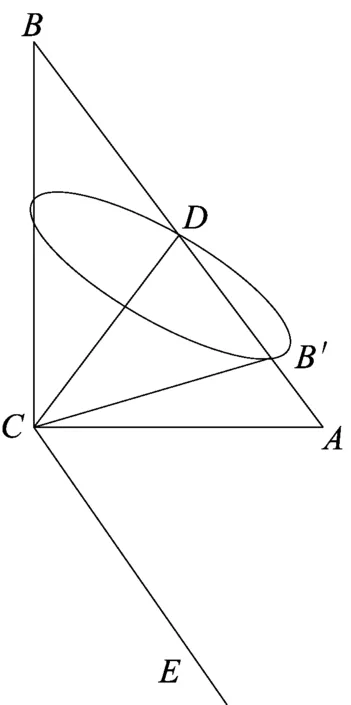
图8-2
例8 (2014年1月浙江省学业水平考试第25题)如图8-1,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
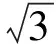
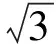
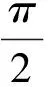
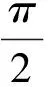
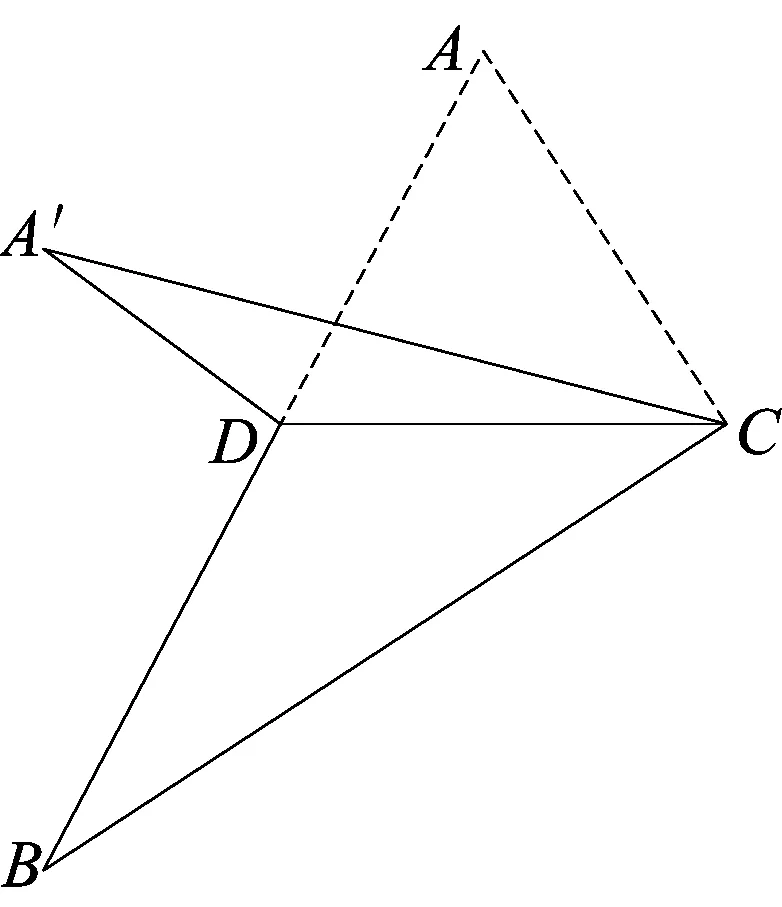
图9-1
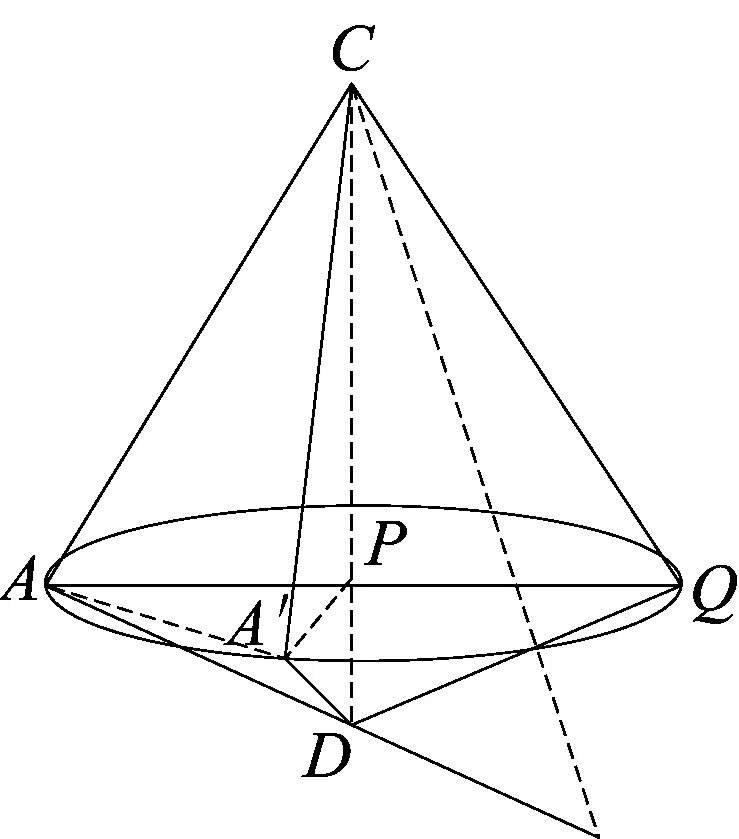
图9-2
例9 (2015浙江高考理科第8题)如图9-1,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
A. ∠A′DB≤α
B. ∠A′DB≥α
C. ∠A′CB≤α
D. ∠A′CB≥α
评注翻折问题是立体几何中一类常见的动态问题.通过对比翻折前后的平面图形和空间图形,找到了我们熟悉的旋转体模型——圆锥,这不仅让空间中的点、线、面在一个具体的空间几何体中找到了落脚处,让问题变得更清晰,有助于我们从宏观的角度来把握问题,也让动态问题变得更具趣味性.
征稿启事
2017年高考、中考已经结束啦,可是对中、高考试卷或试题的研究才刚刚开始.我刊将在第四期、第五期集中优先刊发试题研究方面的优秀论文,欢迎广大读者、作者踊跃投稿.试题研究方面的文章,可以一题一议、多题一议乃至全卷评析,但切忌仅仅给出所谓的新解、别解或简解,变成了解法的罗列,而且应有试题背景分析,思路与解法的生成过程,以及对教学的启示.亲爱的读者、作者,我们欢迎您在第一时间投稿,我们也将会在第一时间刊登您的优秀论文,但不要一稿多投.
投稿邮箱:zsjxhf@sina.com.
《中学数学教学》编辑部
2017-04-12)

