基于改进云自适应粒子群优化算法的NOX含量测量
金秀章,刘 潇
(华北电力大学控制与计算机工程学院,河北 保定 071003)
基于改进云自适应粒子群优化算法的NOX含量测量
金秀章,刘 潇
(华北电力大学控制与计算机工程学院,河北 保定 071003)
脱硝反应器入口NOX浓度的及时、准确测量,对精确调节喷氨量、控制氮氧化物的排放至关重要。针对NOX气体分析仪测量存在的精度差、滞后性等问题,基于传统云理论,并结合径向基函数(RBF)神经网络,提出了改进的云自适应粒子算法(CPSO)-RBF神经网络的测量模型。利用云模型理论中云滴具有随机性、稳定倾向性等特点,提出了一种新型分段式自适应调整粒子群惯性权重算法。利用此优化算法,对神经网络参数进行优化,提高了测量模型的精度。将该模型应用于SCR反应器入口的NOX含量测量中,实例仿真表明,改进算法优化的神经网络模型具有较高的精度,为反应器入口NOX含量的实时、准确测量提供了一定的理论依据,也为实际生产过程中NOX的测量与控制提供了一定的参考。
脱硝反应器; 气体分析仪; 云模型; 粒子群优化算法; 自适应调整; 神经网络; SCR; 软测量; 惯性权重
0 引言
随着环保要求的日益提高,降低污染物排放量已成为燃煤火电站亟待解决的问题。NOX作为主要大气污染物之一,排入大气会引起酸雨和光化学烟雾污染,危害人体健康。国内多数火电站机组都加装了选择性催化还原(selective catalytic reduction,SCR)技术设备,以达到国家烟气脱硝新标准[1]。但此系统存在非线性、大迟延等问题,使系统的稳态控制变得越来越困难[2]。
近年来,韩璞等[3]对神经网络和支持向量机等人工智能技术在热工参数建模领域的应用进行了较详细的阐述。其中,径向基函数(radial basis function,RBF)神经网络是一种前向神经网络模型,与支持向量机相比,它训练速度快、结构简单[4]。输出权重、隐单元中心和宽度这三个重要参数对RBF网络的性能有决定性作用[5]。目前,常采用收敛速度快、易实现性的粒子群算法对参数寻优,但该算法也存在搜索精度低、易陷入局部最优等问题[6]。为改善性能,一些改进粒子群优化(particle swarm optimization,PSO)算法应运而生,如文献[7]提出的改进混沌粒子群算法;文献[8]提出的距离动态变化的粒子群算法;文献[9]提出的云自适应粒子群算法等。
本文基于传统云模型,采用种群适应度分段模式,改进不同惯性权重的生成策略,既保持了种群多样性,又提高了算法收敛速度。将此改进算法运用到 SCR反应器入口NOX含量测量模型上,与传统预测模型相比较,该算法获得了较高的精确度。
1 改进云自适应粒子群优化算法
1.1 云模型
云模型是李德毅等[10]基于传统概率统计和模糊集理论提出的一种不确定性转换模型。假设U是一个论域,U= {x},T是与U相关的语言值。隶属度μ是x对于T的表达,其本质是一个具有稳定倾向的随机数,μ在论域上的分布称为隶属云,简称为云。云由许许多多云滴组成,一个云滴是定性概念在数量上的一次实现,用x表示。
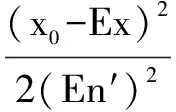
期望值Ex、熵En、超熵He作为表征云模型的3个数字量,通过论域U上的值x0产生云滴(x0,μ) ,这种云生成算法称为X条件云发生器。具体公式如下:
(1)
式中:En′为期望=En、方差=He的正态随机数,所以生成的第i个云滴可表示为(xi,μ) 。
1.2 粒子群优化算法
粒子群优化算法是1995年由Kennedy和Eberhart设计的一种模拟自然界生物之间捕食活动的仿生优化算法。在PSO算法中,每个优化问题的潜在解都可被视为搜索空间中的一个粒子,所有的粒子都有相应的速度,决定了其飞行的方向和距离;同时,每个粒子也具有由被优化函数决定的适应值。算法对一群随机粒子初始化,即其初始位置、速度及其决定的适应值都随机。将第i个粒子在n维解空间的位置和速度分别表示为Xi=(xi1,xi2,…,xin)和Vi=(vi1,vi2,…,vin),再通过迭代找到最优解。每次迭代粒子要通过跟踪如下极值来更新自己的位置和速度:极值是粒子目前的最优解,因每个粒子具有记忆能力,Pbi各自曾经到达的最好位置,这个极值被称为个体极值Pbi=(Pbi1,Pbi2,…,Pbin);另一个极值是整个种群目前的最优解,即全局最优解Nbesti=(Nbesti1,Nbesti2,…,Nbestin)。粒子根据式(2)和式(3),更新自己的速度和位置:
Vi=ωVi+c1rand()×(Pbesti-Xi)+c2rand()×(Nbesti-Xi)
(2)
Xi=Xi+Vi
(3)
式中:c1为认知因子,c2为社会因子,它们分别代表了向自身极值和全局极值推进的加速权值;rand()为0~1的随机数;ω为惯性权重,代表了原速度在一次迭代中所占比重。
ω越大,则表示全局搜索能力越强。在算法初期,取较大ω值对整个空间进行高效的搜索;在算法后期,取较小的ω值,以提高算法的局部搜索能力,利于收敛。因此,ω的取值常用线性递减策略,公式如下:
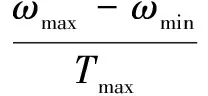
(4)
式中:ω取值通常为[0.8,1.2];Tmax、t分别为最大迭代数和当前迭代数。线性递减策略虽然能满足早期快速搜索全局、精确区域、精细搜索的目的,但ω往往会快速减小,难以在算法初期长时间保持;如果早期搜索因权重过大跳出全局最优点,反而会降低算法的搜寻能力。鉴于此,本文根据粒子的聚集度与适应度,提出了一种新的自适应算法动态调整ω,以提高粒子的全局及局部搜索能力。
1.3 改进的云自适应粒子群算法
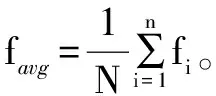
则粒子群的聚集度δ为:
本文改进算法将粒子群体分成3个子群,粒子可根据自身所在种群位置自适应地改变惯性权重ω。具体生成策略如下。
①fi优于favg。
这部分粒子性能接近问题的最优解,其位置的改变不应过大,即惯性权重ω不应太大,从而加快全局收敛的速度。ω可按式(5)调整为:
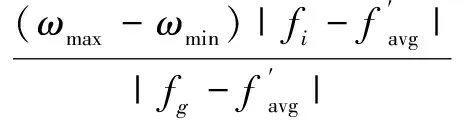
(5)
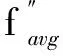
这是群体中性能一般的粒子,使用X条件云发生器,非线性动态地调整粒子的惯性权重ω。云自适应惯性权重生成算法为:
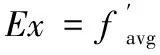
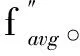
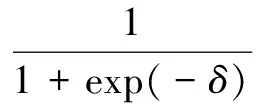
(6)
式中:c为常数;δ为聚集度。多次试验表明,当c=1.5时,粒子的收敛能力和搜索能力较好。聚集度δ较大表明粒子较分散,可减小ω以增强种群的收敛能力;δ较小表明粒子聚集程度高,可增大ω以增强粒子的搜索能力,使粒子具备跳出局部最优的能力。
上述改进的云自适应粒子群算法,不仅保持了粒子的多样性,也平衡了种群全局与局部的搜索能力,使算法具有更快的收敛速度。
2 RBF神经网络
RBF神经网络是一种拓扑结构为单隐层前馈的神经网络学习算法,一般称为3层前馈网或3层感知器。其包括输入层、中间层(也称隐层)和输出层。RBF网络拓扑结构如图1所示。其特点为:同层神经元之间并无联系,而仅与其相邻层之间的神经元相互连接;网络各层神经元之间无反馈连接,从而构成了具有层次结构的前馈型神经网络系统。
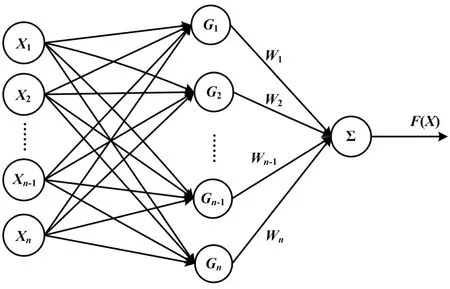
图1 RBF网络拓扑图
图1中:神经网络的训练样本对为{Xn,dn}(n=1,2,...,N);Xn为训练样本的输入,Xn=[xn1,xn2,...,xnM]T(n=1,2,...,N);dn(n=1,2,...,N)为训练样本的期望输出,相对应的实际输出为Yn(n=1,2,...,N);φ(X,ci)为以ci=[ci1,ci2,...,cim,...,ciM](i=1,2,...,I)为中心的基函数;wi(i=1,2,...,I)和σi(i=1,2,...,I)分别为第i个隐元与输出元之间的权值和宽度;n为中心数目。
网络的实际输出为:
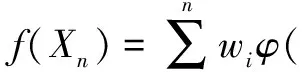
(7)
RBF网络通常选择高斯型函数为基函数,则:
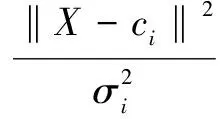
(8)
RBF网络中待定的参数有4个:隐层与输出层之间的连接权重wi,基函数的中心数目n,选取中心ci及宽度σi。n可用减聚类算法确定[11]。wi、ci和σi参数的确定则可以采用优化算法实现。
3 基于CPSO的RBF神经网络学习算法
3.1 适应度函数
每个粒子由wi、ci和σi这3个参数组成。神经网络训练的目的在于搜索使其均方误差和最小的参数组,因此选择平均平方误差为适应度函数。第i个粒子的适应度为:
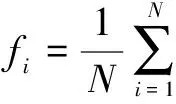
(9)
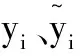
3.2 算法步骤
基于CPSO算法的RBF神经网络学习算法如下。
①采集训练样本。
②采用减聚类算法确定基函数的中心个数。
③初始化粒子群的个数。
④比较每个粒子的适应度值与个体极值Pbest,若f(Pi)>f(Pbest),则Pbest=Pi。
⑤比较每个粒子的适应度值与全局极值Gbest,若f(Pi)>f(Gbest),则Gbest=Pi。
⑥根据文中算法,调整粒子的速度和位置。
⑦重复步骤④~⑥,直到达到计算要求为止。
⑧得到优化的结构参数组,并对RBF神经网络进行学习。
PSO-RBF神经网络算法流程图如图2所示。
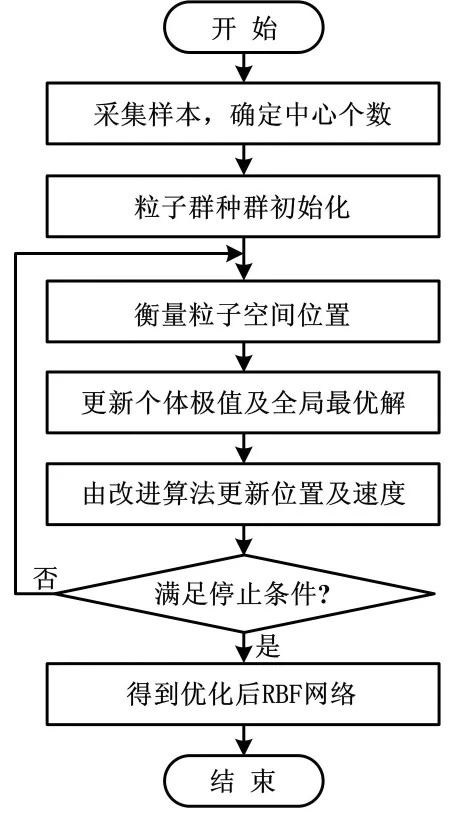
图2 算法流程图
4 SCR反应器入口NOX含量测量
4.1 辅助变量的选择
锅炉系统具有多变量、高耦合性等特点,合适的辅助变量是保证模型精度与复杂度的关键因素,同时选取的辅助变量也是影响主导变量(被测量)的关键因素。该变量必须易获取和测量。
采用某电厂一天的历史运行数据,根据系统设备流程,结合相关文献及NOX生成机理分析,列出了以下辅助变量:总风量、总煤量、风煤比、机组负荷、总一次风量、二次风量、二次风比、给煤量、烟气流量、空预器入口二次风温、磨煤机一次风量加权值、燃尽风风门开度比和磨煤机A~F风煤比。
4.2 样本优选
测量中样本数目往往较多,且原始数据经过插值处理,大量的样本数据必然在一定程度上存在冗余信息。由于样本数据之间的相似度特别高,因此对于大规模的样本集进行优化至关重要。通过数据间的相似度来对样本集进行优选,使剩余的样本尽可能地包含样本集的所有信息,并且相对简单。
根据上文选取的18个辅助变量,每个变量对应10 001个点,以此作为样本集合;利用相似度函数进行样本的优选,剩余样本数量随阈值ε的变化而变化,它们之间的关系如图3所示。
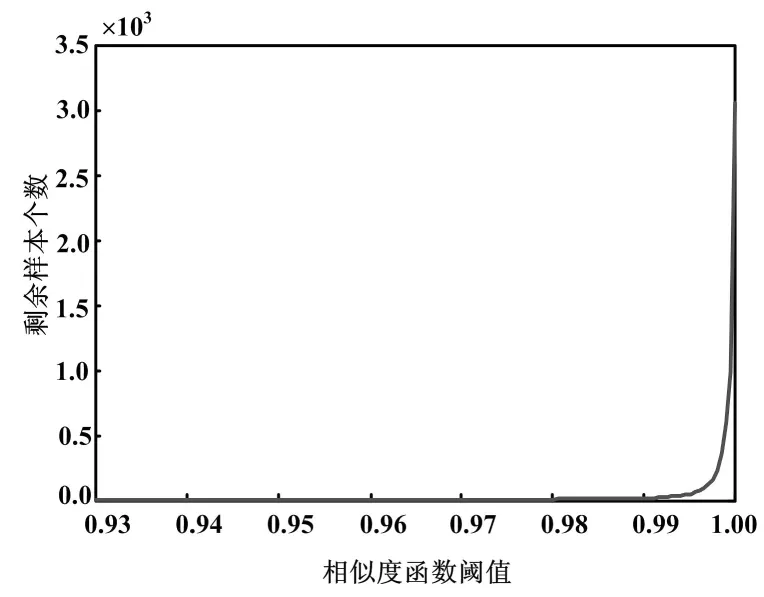
图3 相似度阈值与剩余样本个数关系图
相似度函数为:
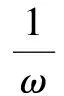
(10)
式中:ω为相似度函数的归一化参数;xi∈R;Rij为第i组与第j组数据样本的相似程度。当Rij大于阈值ε时,剔除一组冗余数据,从而优化样本集合。
如图3所示,随着相似度函数阈值的增大,剩余样本数据的个数也逐渐增加。当相似度函数阈值处于[0.993,1]时,曲线的变化最大,说明此时优化数据样本效率最高,在此区间数据之间存在的冗余信息最多。因此,阈值ε取值应该大于0.997。此时,有179个样本。
4.3 CPSO-RBF神经网络模型的建立
粒子群规模根据训练样本数,选取40个粒子,学习因子为c1=c2=2;神经网络中间层数为6,终止条件为最大迭代次数100或训练误差小于1×10-4。选取优选后的179个样本中的前99个为训练样本,后80个作为测试样本。
将CPSO-RBF模型应用于SCR反应器入口NOX含量的预测,对其与传统RBF、GA-RBF、PSO-RBF神经网络模型进行比较,结果显示CPSO-RBF模型预测值与实测值吻合度高于其余3种模型,预测误差的波动范围也最小。
为了更好地评价模型的精度,分别使用平均误差(average error,AE)、相对均方根误差(relative root mean square error,RRMSE)对模型的预测准确性和变化跟踪能力进行分析[12-13],计算公式如下。
相对均方根误差为:
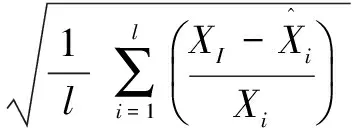
(11)
平均误差为:
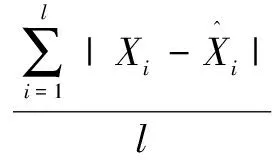
(12)
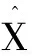
不同模型预测结果分析如表1所示。
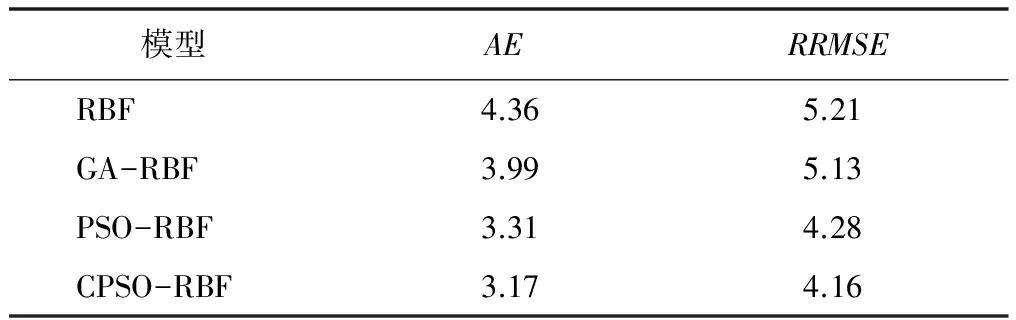
表1 不同模型预测结果分析
由表1可知,基于CPSO-RBF建立的测量模型,其预测结果在各个评价指标中均为最优,证明了CPSO-RBF模型在跟踪能力及预测精度上要优于其他模型。采用本文所述的改进云自适应粒子群优化算法优化的RBF神经网络,建立SCR脱硝反应器入口NOX的测量模型,可以准确预测NOX含量的变化、有效控制喷氨调门动作,防止因大延迟环境下的喷氨不及时造成的NOX排放超标。
5 结束语
本文针对基本粒子群算法全局搜索能力差、易陷入局部最优等问题,基于传统云理论提出了改进的CPSO。利用RBF神经网络建立SCR反应器入口NOX含量的测量模型,并用改进的算法对神经网络参数进行优选。仿真结果表明,优化后的模型与优化前的RBF、GA-RBF、PSO-RBF网络模型相比,能更好地预测脱硝反应器入口NOX的变化趋势,并且获得了较高的准确度,为实际生产过程中的NOX测量与控制提供了一定的参考。
[1] 肖海平,张千,王磊,等.燃烧调整对NOX排放及锅炉效率的影响[J].中国电机工程学报,2011(8):1-6.
[2] 孙克勤,韩祥.燃煤电厂烟气脱硝设备及运行 [M].北京:机械工业出版社,2011.
[3] 韩璞,乔弘,王东风,等.火电厂热工参数软测量技术的发展和现状[J]. 仪器仪表学报,2007,28 (6) :1139-1146.
[4] 蒋宗礼.人工神经网络导论[M].北京:高等教育出版社,2001.
[5] 朱万富,赵仕俊.基于粗糙集的神经网络结构优化设计[J].计算机仿真,2006(4):12 -14.
[6] SHI Y H,EBERHART R C.A modified particle swarm optimizer[C]//Proceeding of IEEE Conference on Evolutionary Computation.Piscataway,1998:69-73.
[7] 韩朝兵,吕晓明,司风琪,等.基于改进混沌粒子群算法的火电厂经济负荷分配[J].动力工程学报,2015(4):312-317.
[8] JIN X,LIANG Y Q,TIAN D P,et al.Particle swarm optimization using dimension selectionmethods[J].Applied Mathematics and Computation,2013,219(10):5185-5197.
[9] 韦杏琼,周永权,黄华娟,等.云自适应粒子群算法[J].计算机工程与应用,2009,45(1):48-50.
[10]李德毅,杜鹃.不确定性人工智能[ M].北京:国防工业出版社,2005.
[11]王洪斌,杨香兰,王洪瑞,等.一种改进的RBF 神经网络学习算法[J].系统工程与电子技术,2002,24(6) :103-105.
[12]唐春霞,杨春华,桂卫华,等.基于KPCA-LSSVM的硅锰合金熔炼过程炉渣碱度预测研究[J].仪器仪表学报,2010,31(3):689-693.
[13]金秀章,韩超.KPCA-LSSVM 在磨煤机一次风量预测中的应用[J].自动化仪表,2015,36 (3):62 -67.
NOXMeasurement Based on
Improved Cloud Adaptive Particle Swarm Optimization Algorithm
JIN Xiuzhang,LIU Xiao
(School of Control and Computer Engineering,North China Electric Power University,Baoding 071003,China)
The timely and accurate measurement of NOXcontent at inlet of denitrification reactor is very important to accurately adjust the amount of ammonia spray and the NOXemission control.Aiming at the problems of the serious delay and poor precision of the NOXgas analyzer,based on traditional cloud theory and combining with the radial basis function(RBF) neural network,the measurement model based on CPSO-RBF neural network is proposed.By using the features of cloud droplets,i.e.,randomness and stable tendency,the new type of segmented adaptive adjustment particle swarm inertia weight algorithm is proposed.The parameters of neural network are optimized using this optimization algorithm,thus the accuracy of the measurement model is enhanced.The model is applied in the NOXmeasurement at the inlet of SCR reactor,the simulation of practical example indicates that the neural network model optimized by the improved algorithm features high accuracy,it provides certain theoretical basis for real time and precise measurement of NOXat inlet of the reactor;and certain reference for NOXmeasurement and control in practical production process.
Denitrification reactor; Gas analyzer; Cloud model; Particle swarm optimization algorithm; Adaptive adjustment; Neural network; SCR; Soft measurement; Inertia weight
金秀章(1969—),男,博士,副教授,主要从事大型发电机组先进控制策略的研究。E-mail:jinxzsys@163.com。 刘潇(通信作者),男,在读硕士研究生,主要从事信号分析与处理、智能控制的研究。E-mail:350788706@qq.com。
TH7;TP273
A
10.16086/j.cnki.issn1000-0380.201707019
修改稿收到日期:2016-10-14

