我国股票市场走势的“历史类似性”分析

李雪晨

摘要：本文基于数学模型考证股指波动的历史类似性，针对2005-2016年上证综指数据，利用神经网络算法对上证综指的走势进行了分析。以开盘价、最高价、最低价、成交量、成交金额5个指标作为BP 神经网络的输入值，以收盘价作为输出值。对我国股票市场走势的“历史类似性”进行分析。

关键词：BP神经网络；上证综指

中图分类号：F830 文献识别码：A 文章编号：1001-828X（2017）013-0-02

一、引言

随着我国日渐成为 21 世纪最重要的国家，国内股票市场的波动，不仅牵动亿万投资者的心弦，也为世界所瞩目。

当前的市场和2009年都经历了快速上涨之后的调整，估值也都已经处于历史中等偏低水平。注意到与2009 年相同的以稳增长为主的政策环境、同样曾经历了大宗商品较大幅度的下跌、投资者关于人民币汇率贬值及经济前景偏于悲观的类似预期，有人认为：“当前市场状况类似迷你版2009”。

二、模型的建立与求解

1.模型的准备

在BP网络的学习过程和定向传递的这一阶段，首先需要导入信号，并且经过内置的算法处理后，将得到的结果输出。在这一过程中积累的误差需要逆向传播到输入的信号，这样一来误差将分摊给该层的所有单元，对这些单元的权值进行修正。不断重复此过程，直到网络输出的误差小于设定值到或进行到预先设定的学习次数为止。

2.数据预处理

我們从2005-2010年定量选取数据作为研究的数据集，该数量暂定为1000，同时为了更好地检验，则选取2014-2016年的500组数据。在进行数据处理前，最好将度量单位统一，归一化可以作为其中的一种方法，做法主要是将数据都转化为[0，1]之间的数。我们将数据集按如下公式进行归一化处理：

其中，xmin为数据序列中的均值，xmax为序列中的最大数。

3.建立BP网络

步骤一：我们建立5-N-1的BP网络结构，其中5表示输入项（开盘价、最高价、最低价、成交量、成交金额），N为隐藏层神经元个数，1表示输出项收盘价。结构图如下：

步骤二：输出结果。根据计算过程中的几个关键参数，包括H，权值和阈值，得出预测的结果。

步骤三：误差计算。误差是由所关注参数的期望值和预测值共同绝对的，其大小等于他们之间的差值，得到的误差值可以为确定隐含层节点数提供依据。

BP神经网络预测的精度在很大程度上是由节点数所决定的，过少地节点数会降低学习的效率，这时不得不以牺牲训练的次数作为代价，但是随之而来了网络过拟合的弊端，因此在确定节点数量的时候通常会参考以下的公式。

其中， n，N，m分别代表输入、隐含和输出层三个不同的阶段的节点数，a为常数，其取值范围位于0和10之间。参考下列公式主要是为了确定节点数的粗略范围，然后通过进一步的测试来获取最佳的节点数，通过多次尝试发现当N=5时，精度已经可以满足相应的要求了。

步骤四：权值更新。根据网络预测误差e更新网络连接权值wij、wjk式中，η为学习速度。

步骤五：阈值确定。由于得到了预测的误差，需要重新定义各个节点的阈值。

学习速度和训练次数对于BP神经网络都有着一定的影响。学习速度和网络训练进程成正比，速度越快，训练越快，速度越慢，训练越慢，但是这不意味着可以一味地增加速度，因为学习速度大会降低网络的收敛性，因此过大的学习速度需要配备更多的训练次数，经过多方位的权衡，最终确定学习速度为0.01，训练次数为100。

4.模型求解

由于之前的归一化处理，因此BP神经网络的输出结果中得到的收盘价也是归一化的，要想得到实际的收盘价，还需要对输出数据进行反归一化。反训练结束的神经网络性能图如下：

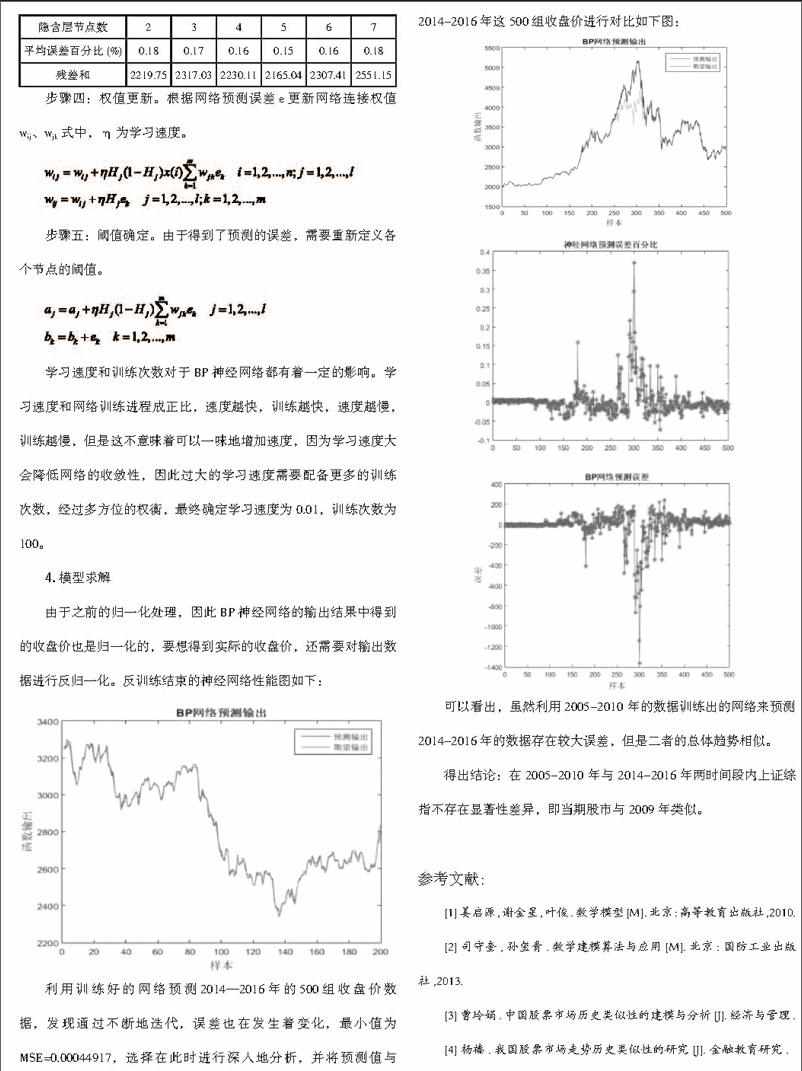
利用训练好的网络预测2014—2016年的500组收盘价数据，发现通过不断地迭代，误差也在发生着变化，最小值为MSE=0.00044917，选择在此时进行深入地分析，并将预测值与2014-2016年这500组收盘价进行对比如下图：

可以看出，虽然利用2005-2010 年的数据训练出的网络来预测2014-2016年的数据存在较大误差，但是二者的总体趋势相似。

得出结论：在2005-2010 年与 2014-2016年两时间段内上证综指不存在显著性差异，即当期股市与 2009 年类似。

参考文献：

[1]姜启源，谢金星，叶俊.数学模型[M].北京：高等教育出版社，2010.

[2]司守奎，孙玺青.数学建模算法与应用[M].北京：国防工业出版社，2013.

[3]曹玲娟.中国股票市场历史类似性的建模与分析[J].经济与管理.

[4]杨榛.我国股票市场走势历史类似性的研究[J].金融教育研究.