版型设计中数据的最优效率方法研究

黄才森，周 莉

(西南大学，重庆 400715)



版型设计中数据的最优效率方法研究

黄才森，周 莉

(西南大学，重庆 400715)

文章针对当前三维制造平台版型设计中数据的最优效率研究有待进一步完善，提出了一种研究方法。该方法是通过捕获三维人体尺寸，从用户数据集群中选取绘制衣片版型(借助EMKO原型设计的部分优点和特殊的人体测量尺寸建立所需的原型结构)所需要的15个用户数据，计算不同覆盖率下的版型对比得分，并且对各组覆盖率与版型对比得分进行最优尺度分析和ROC曲线拟合。依据覆盖率与版型对应得分计算分析结果，结合该覆盖率下三维人体样衣试穿试验验证，最终确定最优效率。

版型设计；覆盖率；曲线拟合

三维人体测量仪可以快速获得三维人体数据，更加科学、方便、准确和快捷地将所测量的服装三维尺寸运用到服装工业的实际生产中来，对于服装产业的发展来说显得尤为重要[1]。近年来，非接触式三维扫描在服装学科的应用开始兴起，从手工测量逐渐向自动化、数字化转变的趋势越发明显。服装个性化定制的需求不断上升，因此沿用服装推放码原则进行生产的方式越来越不能满足用户个性化的需求。本文正是基于人体尺寸与版型绘制的关系，探讨寻求最优效率，更好地推进电子化量身定制。

1 引言

在标准样版到个性样版的转换过程中，有研究提出通过确定关键点，建立点编号和修改规则的方式进行传统放码[2-3]；还有研究提出根据顾客人体数据信息快速生成适合该顾客的样版为核心的量身定做系统[4]。这些方法都存在一定的局限性，并且对打版技术人员要求较高。针对此类现状，本文提出精确采集用户数据，从原型衣片比较到系统分析的精准验证，实现个性样板最优方案，如图1所示。

图1 研究流程图

2 原型对象的选取与绘制

2.1 原型对象选取原则

原型设计方法需要充分考虑人体结构特点，同时为了趋向服装个性化定制，需要采用足够多的人体标准尺寸[5]。

2.2 原型比对

2.2.1 美式原型

由于其胸省位于腰省的位置上，因此外观造型更加立体，但是胸部上部不会很服帖,总计使用人体尺寸22个。

2.2.2 英式原型

胸省在肩缝上，传统欧洲原型的外观特点更加容易使服装合体，竖向分割线也更加趋近人体的线条,总计使用人体尺寸10个。

2.2.3 日本文化式原型

基于完善的测体数据之上，根据测体数据之间的回归关系而将使用尺寸缩减到4个，其结构与服装立体裁剪有着密切的关系,总计使用人体尺寸4个。

2.2.4 东华原型

在参照日本文化式原型的基础上根据我国的测体数据建立起来的，并在不断地调整和完善中，总计使用人体尺寸4个。

2.2.5 俄罗斯的EMKO原型

运用大量人体测量尺寸(47个)及其几何近似运算，充分考虑到了人体结构特点，并采用了足够多的人体标准尺寸，因此既可以在服装定制中使用，也可以广泛运用到工业生产。为了凸显本文研究特点，使用的原型设计方法是借助EMKO原型设计的部分优点和特殊的人体测量尺寸建立所需的原型结构。

2.3 原型绘制

在原型绘制过程中，共包括56个步骤，涉及到50个单位点和6段单位弧长的绘制。经过简化和统计，绘制过程共使用15个人体测量尺寸。由于篇幅的限制，绘制步骤不在此详述，衣片原型设计结果如图2所示。

图2 衣片原型的绘制

3 最优效率的数据分析与验证

3.1 覆盖率与版型对比得分的计算

为了统计15个用户数据在版型绘制中的使用频率和权重，现对构成点和弧长的原始数据进行计算和分析，结果如表1所示。

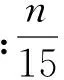
表1 人体尺寸数据统计表

则在版型绘制步骤的56个单元，Tm总得分为：

因此，可以依次计算使用n(n∈[1,15])且n∈N+)个人体尺寸的版型对比得分：

计算结果如表2所示。

表2 覆盖率划分结果

注：表2中人体尺寸(序列号)列沿用表1序列号，下同。

3.2 ROC曲线拟合和最优尺度回归

由于表2中罗列的数据不能直观地观测版型对应得分与覆盖率之间的变化关系，本文对表2进行散点图的绘制，结果如图3所示。在散点图基础上完成ROC曲线拟合，结果如图4所示。

本文选用SPSS 19.0数据统计分析软件对版型对应得分与覆盖率的散点图进行ROC曲线拟合。根据散点图的趋势，同时进行Linear线性模型、Inverse倒数模型、Cubic抛物线模型和Logarithmic对数模型4种函数类型的拟合。结果见图4。

图3 覆盖率与版型对应得分散点图

从图4中可以反映出4种函数模型对数据的拟合程度不尽相同。函数模型拟合程度的高低一定程度上反映于方差F和调整R平方的数值[10]。函数类比结果如表3所示。

表3 函数类比结果

表3的统计结果显示，在这4种函数类型中，抛物线函数模型的调整R平方和方差最小，而且从图4中也可以看出，4段函数曲线中，抛物线函数模型的拟合程度最优。

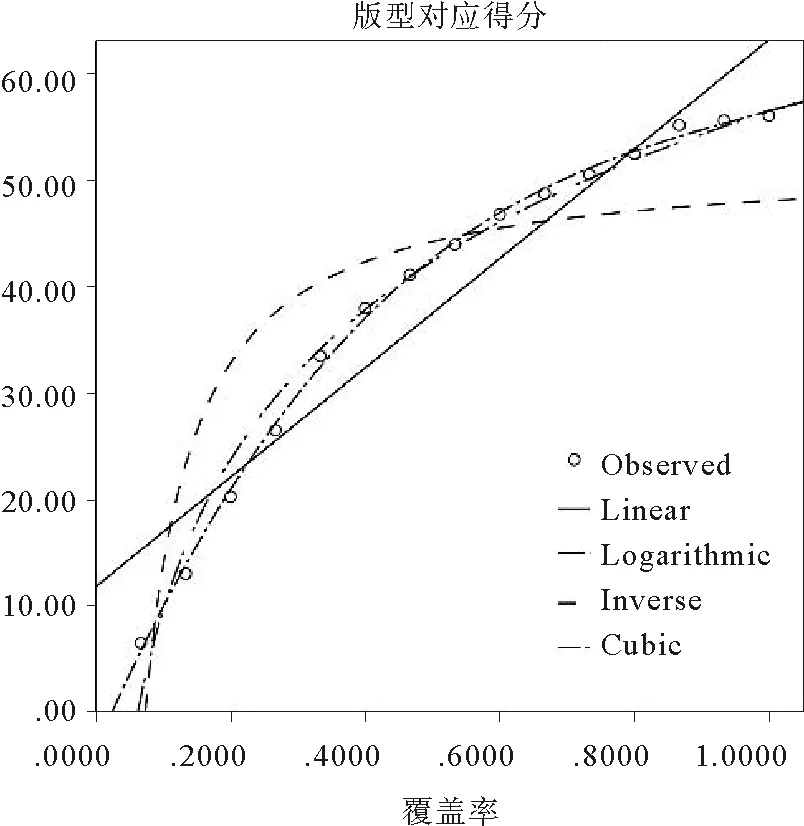
图4 覆盖率与版型对应得分曲线拟合图

由于版型对应得分与覆盖率是一一对应且为点集，因此不适合采用对拟合抛物线函数模型求导函数的方式进行最优解的计算。本文通过计算并观测15组覆盖率下的版型对应得分与用户数据覆盖率的比值，依据此项指标为参照，代入抛物线函数检验求最优解。为保证数据采集的合理性和本文研究的必要性，将覆盖率大于等于80%和小于等于20%的相应数据剔除。最终计算结果如表4所示。

表4 比值计算结果

从表4中可以发现，在覆盖率为33.33%时，版型对应得分与覆盖率的比值最高，通过计算抛物线函数模型在该点的切线斜率与其余点相比较验证发现，覆盖率为33.33%时绘制版型数据转置效率最优。

3.3 三维操作平台试验验证

本文选用CLO3D 2011软件对图2原型衣片分别进行用户数据覆盖率为100%和33.33%的原型绘制比较。如图5、图6所示。

图5 覆盖率33.33%三维虚拟试衣

在CLO3D软件界面的进行版的绘制，覆盖率为33.33%时，与胸高、前腰节长、背宽、后中长和臂根宽有关的工艺数据被确定，其余数据可以人工调节，可以为用户提供更高效的个性化定制。在适体性上，与覆盖率为100%的版型相较而言，更有可能适合不同体型特征的用户客群。

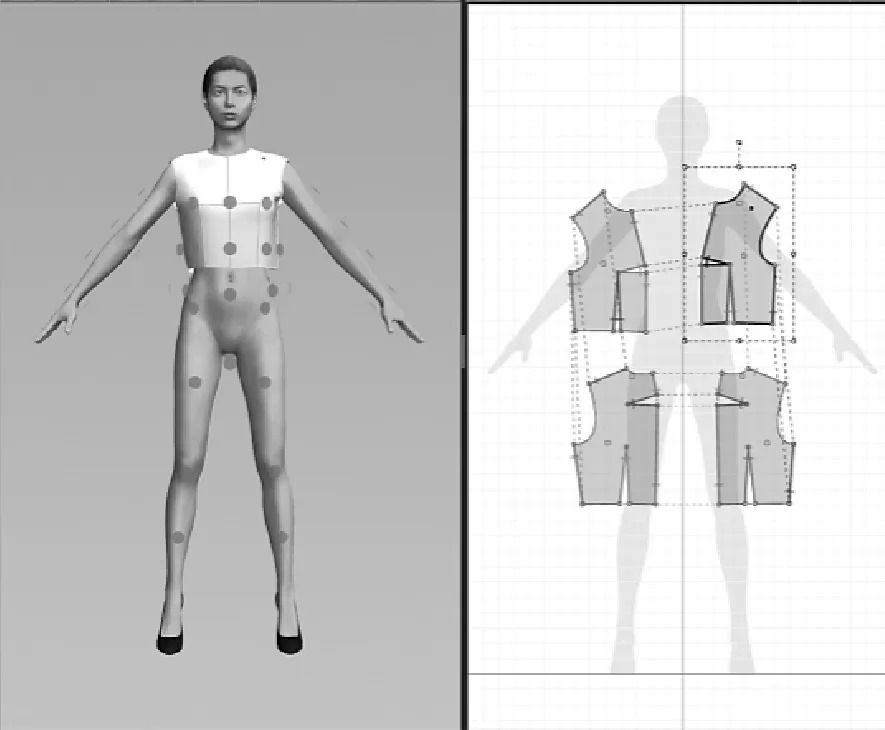
图6 覆盖率100%三维人体试穿

4 结论

本文借助EMKO原型设计的部分优点和特殊的人体测量尺寸建立所需的原型结构为研究对象，提取原型绘制所需要的用户数据，经过数据处理和ROC曲线拟合，拟合结果显示覆盖率为33.33%时效率最优，对应的用户数据为：胸高、前腰节长、背宽、后中长、臂根宽。将最优效率下的覆盖率在CLO3D上进行原型验证。从验证过程来看，在原型绘制时确定覆盖率为33.33%对应的用户数据以外，其余变量根据体型进行人工调节，通过适体性和效率综合比对，覆盖率为33.33%最优。因此，在选取本文所建立的原型作为基础版投入生产时，应缩减采集用户数据为胸高、前腰节长、背宽、后中长和臂根宽效率最优。用户数据的采集在不同版型之间存在一定差异，但是本文在研究方法上普遍适用。

[1] 温武.基于三维人体测量数据的服装结构设计应用研究[D].天津：天津科技大学，2010.

[2] Cynthia L，Istook. Enabling Mass Customization: Computer-driven Alteration Methods[J].International Journal of Clothing Science and Technology，2002，14(1)：61—76.

[3] 杨允出，张渭源，刘莉.基于批量定制的服装样板数字化设计技术[J].纺织学报，2007，28(1)：124—128.

[4] 胡觉亮，董建明，何瑛，等.基于人工神经网络的服装结构设计[J].纺织学报，2006，27(2)：49—52.

[5] 齐行祥.基于个性化虚拟人台的服装合体性评价模型研究[D].上海：东华大学，2011.

Research on Optimal Efficiency of Data in Pattern Design

HuangCaisen,ZhouLi

(Southwest University, Chongqing 400715, China)

The article pointed out a research method to improve the optimal efficiency of the data in pattern design, which used the three-dimensional manufacturing platform. This method measured three-dimensional sizes of the human body, selected 15 required body sizes of drawing pattern (which was designed with the advantages of EMKO pattern and special human body measurement dimensions) from the data cluster, calculated the pattern type contrast score under different coverage ratio, fitted ROC curve and analyzed the optimal scale of the coverage ratio and pattern contrast score. According to the result of calculating and analyzing the coverage ratio and pattern contrast score, and combined the experimental verification of 3D human body sample under the coverage ratio, the optimal efficiency could be confirmed.

pattern design; coverage ratio; curve fitting

2017-04-08

中央高校基本业务费专项资金资助项目(XDJK2016C100、XDJK2014A011)

黄才森(1996—)，男，江西赣州人，学士。

TS941.2

A

1009-3028(2017)03-0040-05