基于改进卡尔曼滤波算法的雷达定量降雨估算*

曲小康，芮小平**，于雪涛，雷秋良



基于改进卡尔曼滤波算法的雷达定量降雨估算*

曲小康1，芮小平1**，于雪涛2，雷秋良3

(1.中国科学院大学资源与环境学院，北京 100049；2.石家庄铁道大学交通运输学院，石家庄 050043；3.中国农业科学院农业资源与农业区划研究所/农业部面源污染控制重点实验室，北京 100081)

针对雷达定量降雨估算误差较大的问题，本文提出一种使用改进卡尔曼滤波对雷达估算值进行校准的方法。先确立G/R（自动气象站测量值/天气雷达估算值）校准因子模型，并应用普通卡尔曼滤波方法对G/R校准因子建立预测系统和测量系统，同时引入系统参数的校准过程和系统误差的自适应估计过程，动态调整卡尔曼滤波中各项参数值；最后将滤波后的G/R因子用于校正雷达定量降雨估算，得到较准确的降雨估算值。利用长春市天气雷达2015年8月19-20日和2016年月8月6-7日两次降雨过程的雷达产品和加密自动站逐小时的降雨资料，对卡尔曼滤波方法进行检验分析。结果表明：改进卡尔曼滤波和普通卡尔曼滤波校准后雷达降雨估算结果优于未校准的降雨估算结果，普通卡尔曼滤波方法和改进卡尔曼滤波方法的平均相对误差分别从0.6047减至0.3557和0.2645，从0.8052 减至0.3096和0.1715，且改进算法效果优于普通卡尔曼滤波算法，校准后雷达降雨估算准确度明显提高。

G/R校准因子；改进卡尔曼滤波；定量降雨估算；自适应估算

高时空分辨率的雷达定量降雨估算对暴雨、洪水等各种强对流天气引起气象灾害的监测及预警具有十分重要的意义。雷达的降雨估算常用经验关系模型Z=aIb（a、b为模型参数值，Z为雷达反射率因子，I为降雨强度）来估算降雨强度，但是雷达探测过程中由于受到各种地物杂波、雨滴、超折射等因素影响，其雷达反射率值的系统误差不可能完全消除；同时不同地区或不同的降雨过程模型中，a、b参数值也存在较大的差别，导致雷达降雨估算值与实际降雨量偏差较大[1]。

为了获取较为准确的雷达降雨估算值，通常利用G/R（即自动气象站测量值/天气雷达估算值）校正雷达估算值，现有G/R的获取方式主要有平均校准法、变分法及卡尔曼滤波法等。卡尔曼滤波作为一种线性无偏最小方差递推滤波，在雨量站与雷达联合估算降雨过程中具有广泛应用。1986年Ahnert等首次提出利用卡尔曼滤波方法对G/R校准因子实时预测的方法，并指出该方法具有修正测量噪声、显示估算误差及避免G/R不稳定的优势[2]。此后研究者应用卡尔曼滤波针对不同降雨类型或地区进行校验分析，研究成果主要体现在两个方面：（1）改进G/R校准因子模型，使之适合不同的降雨类型，提高利用卡尔曼滤波优化降雨估算效果，如：Chumchean提出log10(G/R)校准模型对于雨量站较少地区具有较好的滤波效果[3]；Sharifah等综合考虑分析温度、湿度等气象要素对卡尔曼滤波效果的影响，并提出了多因素校准因子模型[4]。（2）改进卡尔曼滤波方法预测过程和测量过程中的参数取值，提高卡尔曼滤波算法的稳定性及收敛速度，如：尹忠海等分析了模型中各项参数对估算结果影响，为改进各项参数提供建议[5]，Monteiro等对预测方程中状态方程转移矩阵参数通过降雨数据统计分析，得到较优结果参数[6]；徐燕等提出利用自适应滤波方法估算模型参数的方法，提高滤波估算的精度[7-8]。赵坤等利用卡尔曼滤波与变分法结合方式优化模型中参数值，提高雷达降雨估算准确性9]。在利用卡尔曼滤波进行校准雷达降雨估算的研究中，校准因子确立多与固定降雨类型或雨量站疏密相关，其模型已比较成熟；而滤波算法则由于其参数主要设为经验常数，存在对不同的降雨过程或者较短降雨适应性差的问题，降低了滤波算法校准的精度，影响雷达降雨估算准确性，因此这也是本研究主要改进的方向。

本文在前人研究基础上，对普通卡尔曼滤波引入了卡尔曼状态参数模型和极大似然估计准则方法，分别对卡尔曼滤波算法过程中每一步的状态模型参数值、状态方程及测量方程的噪声值进行修正，以减少由于模型参数设置不合理对整个滤波过程的影响，增强滤波算法的稳定性，从而有效提高雷达定量降雨估算的准确性。

1 资料与方法

1.1 资料及处理

以吉林省长春地区2015-08-19 T1：00—20 T22：00和2016-08-06 T17：00—07 T06：00两次降雨过程为研究对象，采用长春气象雷达基站数据和加密自动站逐小时的降雨资料。长春气象雷达基站为CINRAD/CC系列雷达，天气雷达探测空间分辨率为300m，时间分辨率为6min，探测范围为150km，天线高度为290m，雷达站与自动气象站的分布如图1，其中80%气象站用于试验，剩余气象站则用于试验结果检验。

雷达资料采用3km高度CAPPI产品数据，用某一时刻的不同仰角扫描资料插值成相同高度的反射率因子场资料，同时为了排除杂波的影响，将反射率小于15或大于78的数据剔除，因为反射率小于15被看作不会引起降雨，而大于78极可能是冰水混合物，也不会引起降雨[10]。

由于自动气象站观测值代表某个点上1h的降雨量，而雷达探测值为反射率因子，存在空间及时间上差异。为了统一比较，以气象站为基准，对雷达资料进行以下处理。

（1）雷达极坐标数据转换网格平面直角坐标系，网格分辨率与雷达原始数据极坐标的最小分辨率相同，为0.3km×0.3km。

（2）每隔6min获取雷达基数据资料，并生成等高平面反射率场（CAPPI），根据式（1）估算该时刻的降雨强度，并将1h内计算的降雨强度加权累加，生成1h内的雷达降雨估算值，建立雷达降雨估算值初始场。

Z=aIb（1）

式中，Z为反射率因子，I为降雨强度，a、b为模型参数[8]。

（3）根据自动气象站坐标，选取雷达降雨估算场中与自动站相邻的12个有效数据，对有效数据通过加权平均的方式计算与该气象站相同位置的雷达降雨估算值。

1.2 普通卡尔曼滤波算法

卡尔曼滤波算法是对一个随机变量建立2个独立估计方程，得到估计值，然后通过选择合适的权重因子对两个估计值进行加权平均得到滤波后输出变量的过程，本文将G/R校准因子作为卡尔曼滤波算法中的随机变量x。

卡尔曼滤波算法主要分为预测过程和测量过程，前者是用前一时刻变量的估计值得出当前时刻的先验估计值，后者是用当前时刻的测量值来更正上一过程中的先验估计值，得到当前时刻的后验估计值[11]。其具体递推计算过程为

预测过程：

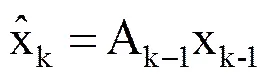
（3）

测量过程：

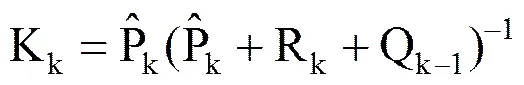
（5）

（6）

式（1）-式（6）为普通卡尔曼滤波的算法计算具体过程，但是在普通卡尔曼滤波方法中，状态方程中转移矩阵A以及 Q和R的误差均假定为先验常数值，这对复杂的降雨系统来说显然是不合理的。

1.3 卡尔曼滤波算法的改进

为了适应复杂降雨系统变化的特点，对普通卡尔曼滤波算法中参数进行以下两个方面的改进：

（1）将式（2）中的转移矩阵A 看作是一个时间变量，对变量A也建立普通卡尔曼滤波的状态方程和测量方程，然后用滤波后的A值代入G/R校准因子滤波过程中，从而提高状态方程的准确性。

（2）基于极大似然准则，对Q和R误差进行实时估计和调整，以实时反映系统模型的变化，使卡尔曼滤波器能够跟踪系统模型的变化。其推导过程为

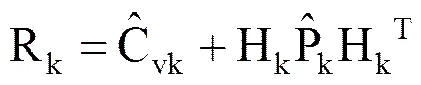
（8）

（9）

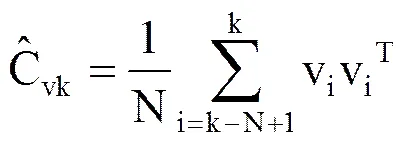
2结果与分析

2.1 改进卡尔曼滤波估算的模型

本文将没有经过滤波的校准因子设为

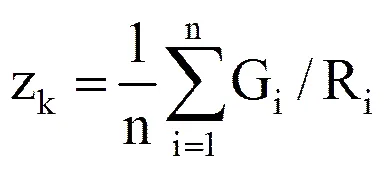
其中，n为参加校准的自动气象站的总数，Gi为第k时刻内气象站测得的降雨量值，Ri为与气象站同一位置的雷达降雨估算值，该值由1.1节中建立的雷达降雨估算值获取，式（1）中模型参数a=300，b=1.4[14-15]。

卡尔曼滤波算法过程0时刻参数值为：x0=0；P0=0.01，Q0=0.25，A0=1。

2.2 改进卡尔曼滤波算法的流程

改进卡尔曼滤波算法是通过对校准因子进行滤波处理，间接调整雷达降雨估算的初值场，达到对雷达降雨估算的校准，其主要计算流程（图2）为

（1）赋初值，k=0，k=[0, n]，n为一次降雨过程中雷达和自动气象站资料有效记录的小时数；x为校准因子，即G/R的预测值，设置x0=0；Qk和Pk分别为状态系统误差和测量系统误差，在0时刻，设置P0=0，Q0=0；状态转移A 假设为1。

（2）在预测过程中，右侧为状态转移矩阵A的预测过程，左侧为校准因子的预测过程。在左侧的状态方程中Ak-1值是k-1时刻基于A的滤波过程输出的后验估计值，然后根据左侧状态系统得到k时刻x变量的先验估计值；右侧的状态方程中假设其状态转移矩阵恒为1，然后得到k时刻A的先验估计值。

（3）根据式（1），对k时刻内的雷达数据进行处理，建立k时刻雷达降雨估算初值场。

（4）输入气象自动站降雨测量数据，根据式（11）计算k 时刻内G/R校准因子的值，即Zk，没有经过滤波的校准因子，如果该值不存在有效值，则重新计算下一时刻的预测过程；如果该值存在有效值，要同时进行状态转移矩阵A和校准因子x变量的测量校正过程，求解卡尔曼滤波的方程组，这两个变量的测量过程Q和P为相同的值，最后得到k时刻的状态转移矩阵A和校准因子x的后验估计值，即得到k时刻内最优的校准因子xk。利用最优校准因子可对k时刻的雷达降雨估算初值场进行校正[16]。

（5）如k＜n，则重复过程2、3、4，即可得到每时刻内较优的校准因子值。

2.3 改进卡尔曼滤波算法结果

2.3.1 G/R比值

研究区域为长春市雷达基站有效探测范围，将研究区域分为试验区域和评估区域。试验区域就是利用雷达资料和自动气象站数据通过卡尔曼滤波方法获取G/R后验估计值，而评估区域则是利用估算出的G/R 校准因子对雷达估算进行校正，并与评估区域内气象站的实测值进行对比评估[17-18]。

由图3可见，在两次降雨过程中，改进卡尔曼滤波G/R比值随时间的变化与实际值较吻合，收敛速度较快，有较强的自适应能力，与实测值的偏差较小。而普通卡尔曼滤波G/R比值的变化与实际值偏差较大，收敛速度较慢，受试验样本的影响较大，当时间序列中出现较大值时，估算值与实测值的偏差较大。

由图中还可看出，样本数量对卡尔曼滤波的影响较大。对于普通卡尔曼滤波，样本数量较大（图3a）的降雨过程，滤波值趋于收敛，逐渐稳定；样本数量较小（图3b）的降雨过程，则收敛很慢。而改进卡尔曼滤波则受试验样本的影响较小，两次降雨过程中的收敛速度均较快，因此，对于时间较短的降雨过程，改进卡尔曼滤波表现出更好的收敛效果。从两次降雨过程的估计值与实测值的比较（图4）也可以看出，改进卡尔曼滤波法的点较聚集，而普通卡尔曼滤波的点较分散，改进卡尔曼滤波校准的G/R估计值与实测值相关性较大，两次降雨过程相关系数从0.1245、0.3721分别提高至0.7295、0.6222。

2.3.2 误差分析

对于两次降雨过程，利用G/R校准因子对评估区域内的雷达降雨估算值进行校正计算，得到校准后的雷达降雨估算值，并与评估区域内的雨量站数据进行对比分析[19]。

由图5可以看出，在两次降雨过程中，相比未校正的雷达降雨估算值，改进卡尔曼滤波校正后估算小时雷达降雨量的绝对误差相对较小，基本在0～1mm区间，而普通卡尔曼滤波计算小时雷达降雨量的绝对误差在0～2 mm区间。从表1也可以看出，两种卡尔曼滤波方法都能解决由于Z-R关系模型参数的适应性差以及雷达估测系统本身误差造成的雷达估测值偏小的问题，2015年8月19-20日降雨过程中小时降雨量的平均相对误差从0.6047分别减至0.3557和0.2645，分别减少了41%和53%，均方根差从1.5246减至0.9794和0.6928；2016年8月6-7日降雨过程平均相对误差从0.8052分别减至0.3906和0.1715，分别减少51%和85%，均方根差从1.3596 减至0.3131和0.2163，说明卡尔曼滤波算法有效提高了雷达定量降雨估算的精度，同时可以看出，相比普通卡尔曼滤波，改进卡尔曼滤波在估算的准确性及稳定性方面均有明显提高。

表1 两次降雨过程不同方法估算小时降雨量的误差比较

2.3.3 降雨量分布

利用卡尔曼滤波修正的G/R因子校准原始的雷达降雨估算值，可以看出，对两次降雨过程校准后的雷达降雨估算值，改进后的卡尔曼滤波校准要好于普通卡尔曼滤波，而且通过两次降雨过程对比，当试验的降雨过程时间较长时，其校准效果较好。

为了研究降雨场空间分布，对2015年8月19日1：00-2：00某一区域的降雨量估算值进行校准分析，据统计，在2015年8月19日1：00-2：00有52个雨量计测量数据有效，再利用地理学方法对雨量计观测值进行插值，获得面上的降雨量分布状况（图6a），雷达估算的降雨量及校准后的降雨量分布如图6b、图6c。由图可以看出，雷达和雨量计基本都能显示出降雨的大致范围，降雨中心也较明显，但是雷达的测雨中心小于雨量计测的降雨范围，而经过修正后的卡尔曼滤波校准的雷达回波图像与雨量计通过插值方式获得的降雨范围图像基本符合，更能够突出降雨的强度中心，在实际应用中，准确的雷达定量降雨估算更有利于降雨量区域分析。

3 结论与讨论

（1）G/R校准模型同时受雷达降雨估算模型与自动站实测因素影响，在降雨过程不同阶段或不同降雨地区存在一定差异，卡尔曼滤波校准时，对于较长时间的降雨过程，其变化范围较小，且趋于稳定；而对于较短时间降雨过程，则变化范围较大，表现不稳定[17]。因此对于较长降雨过程，能够得到更好的雷达估算降雨效果。

（2）初值及模型参数设置对卡尔曼滤波校准方法的估测精度影响较大，不同于之前研究中如赵坤等将卡尔曼滤波方法的模型参数设置为经验常数值[9]，改进后卡尔曼滤波方法对每一步状态方程和测量方程中参数进行修正，减少参数设置不合理对整个滤波过程影响，提高滤波算法的自适应能力。在试验中两次降雨过程的相关系数分别从 0.1245提高到0.7295，从0.3721 提高到0.6222，提高了G/R校准因子的准确性，从而使校正后雷达降雨估算值也得到提高。

（3）本研究将滤波输出的G/R比值应用于雷达降雨估算初值的校正过程，结果表明：普通卡尔曼滤波方法分别将平均相对误差从0.6047减至0.3557，从0.8052 减至0.3096；而改进卡尔曼滤波方法分别将平均相对误差从0.6047减至0.2645，从0.8052 减至0.1715，相比普通卡尔曼滤波方法，改进后的方法更好地提高了雷达定量估算区域降水的精度，同时经过改进卡尔曼滤波校准后的雷达估算场，能够突出强降雨中心区域以及补充自动气象站未测量的降雨区域。而相比于其它雷达估算校准方法，如动态分级法等，提出的卡尔曼滤波则不需要大量试验数据计算，同时能够输出滤波方差的特点，更有利于对校准系统进行评估及优化[20]。

本文试验考虑了长春地区的两次不同年份降雨过程，但是平均降雨量均较少，缺少不同类型降雨过程的验证分析，为了提高改进的卡尔曼滤波在实际雷达定量降雨估算中的适用性，还需对大量的降雨过程进一步研究。

References

[1]郑媛媛,谢亦峰,吴林林,等.多普勒雷达定量估测降水的三种方法比较试验[J].热带气象学报,2004,(2):192-197.

Zheng Y Y,Xie Y F,Wu L L,et al.Comparative experiment with several quantitative precipitation estimator techniques based on Doppler radar[J].Journal of Tropical Meteorology, 2004,(2):192-197.(in Chinese)

[2]Ahnert P R,Krajewski W F,Johnson E R.Kalman filter estimation of radar-rainfall field bias[C].Preprints,23rd Conf.On Radar Meteor.,Snowmass,CO,Amer.Meteor.Soc., 1986:33-37.

[3]Chumchean S,Seed A,Sharma A.Correcting of real-time radar rainfall bias using a Kalman filtering approach[J].Journal of Hydrology,2006,317(1):123-137.

[4]Sharifah N H S Y,Wardah T,Suzana R,et al.Improved estimation of radar rainfall bias over Klang River Basin using a Kalman filtering approach[J].Bandung:2012 IEEE Symposium on Business,Engineering and Industrial Applications,2012: 368-373.

[5]尹忠海,张沛源.利用卡尔曼滤波校准方法估算区域降水量[J].应用气象学报,2005,(2):213-219.

Yin Z H,Zhang P Y.Radar rainfall calibration by using the Kalman filter method[J].Journal of Applied Meteorological Science,2005,(2):213-219.(in Chinese)

[6]Monteiro M,Costa M.A comparison between single site modeling and multiple site modeling approaches using Kalman filtering[A].Proceedings of the international conference on numerical analysis and applied mathematics 2014(ICNAAM- 2014)[C].AIP Publishing,2015,1648(1):110003.

[7]徐燕.卡尔曼滤波法在西峰雷达估测降水中的应用[J].干旱气象,2008,(1):78-82.

Xu Y.Application of Kalman filter in precipitation estimation by radar[J].Aridity Meteorology,2008,(1):78-82.(in Chinese)

[8]Kim J,Yoo C.Use of a dual Kalman filter for real-time correction of mean field bias of radar rain rate[J].Journal of Hydrology,2014,519:2785-2796.

[9]赵坤,刘国庆,葛文忠.用卡尔曼滤波确定变分方法中的权重系数进行雨量校正[J].气候与环境研究,2001,6(2): 180-185.

Zhao K,Liu G Q,Ge W Z.Precipitation calibration by using Kalman filter to determine the coefficients of the variational equation[J].Climatic and Environmental Research,2001,6(2): 180-185.(in Chinese)

[10]勾亚彬,刘黎平,杨杰,等.基于雷达组网拼图的定量降水估测算法业务应用及效果评估[J].气象学报,2014,72(4): 731-748.

Gou Y B,Liu L P,Yang J,et al.Operational application and evaluation of the quantitative precipitation estimates algorithm based on the multi-radar mosaic[J].Acta Meteorologica Sinica,2014,72(4):731-748.(in Chinese)

[11]刘勤,严昌荣,何文清.黄河流域干旱时空变化特征及其气候要素敏感性分析[J].中国农业气象,2016,37(6):623-632.Liu Q,Yan C R,He W Q.Drought variation and its sensitivity coefficients to climatic factors in the Yellow River Basin[J].Chinese Journal of Agrometeorology,2016,37(6): 623-632.(in Chinese)

[12]王学斌,徐建宏,张章.卡尔曼滤波器参数分析与应用方法研究[J].计算机应用与软件,2012,(6):212-215.

Wang X B,Xu J H,Zhang Z.On analysis and application approach for Kalman filter parameters[J].Computer Applica- tions and Software,2012,(6):212-215.(in Chinese)

[13]岳晓奎,袁建平.一种基于极大似然准则的自适应卡尔曼滤波算法[J].西北工业大学学报,2005,23(4):469-474.

Yue X K,Yuan J P.An adaptive Kalman filtering algorithm based on maximum-likelihood criterion[J].Journal of Northwestern Polytechnical University,2005,23(4):469-474. (in Chinese)

[14]殷志远,沈铁元,彭涛.基于雷达和雨量站的权重校准法研究及其应用[J].人民长江,2010,(2):47-51.

Yin Z Y,Shen T Y,Peng T.Research and application of weight calibration method based on radars and rainfall stations[J]. Yangze River,2010,(2):47-51.(in Chinese)

[15]杨杰,刘黎平,赵城城,等.雷达估测对流性降水的误差空间分布及Z-R关系的优化[J].高原气象,2015,34(6):1785-1796.

Yang J,Liu L P,Zhao C C,et al.Spatial distribution of error from the convective precipitation estimation of radar and optimization of Z-R relationship[J].Palateau Meteorology, 2015,34(6):1785-1796.(in Chinese)

[16]东高红,吕江津.不同校准方法检验雷达定量估测降水的效果对比[J].气象与环境学报,2012,28(4):38-42．

Dong G H,Lv J J.Comparison on quantitative estimation of precipitation using radar based on different calibration methods[J].Journal of Meteorology and Environment,2012, 28(4):38-42.(in Chinese)

[17]程进伟,李建勋.卡尔曼滤波算法评估平台的设计与实现[J].系统仿真学报,2013,(11):2567-2574.

Cheng J W,Li J X.Design and implementation of software platform to evaluate Kalman filter algorithm[J].Journal of System Simulation,2013,(11):2567-2574.(in Chinese)

[18]张利平,张晓琳,王任超,等.雷达估算降雨的同化方法对比[J].武汉大学学报(工学版),2011,(2):146-150.

Zhang L P,Zhang X L,Wang R C,et al.The compare research of the rainfall data assimilation methods based on the radar[J].Engineering Journal of Wuhan University,2011,(2): 146-150.(in Chinese)

[19]Marco C,Teresa A.Parameter estimation of state space models for univariate observations[[J].Journal of Statistical Planning and Inference,2010,140(7):1889-1902.

[20]汪瑛,冯业荣,蔡锦辉,等.雷达定量降水动态分级Z-I关系估算方法[J].热带气象学报,2011,27(4):601-608.

Wang Y,Feng Y R,Cai J H,et al.An approach for radar quantitative precipitation estimate based on categorical Z-I relations[J].Journal of Tropical Meteorology,2011,27(4):601- 608.(in Chinese)

Quantitative Rainfall Estimation Using Weather Radar Based on Improved Kalman Filter Method

QU Xiao-kang1, RUI Xiao-ping1, YU Xue-tao2, LEI Qiu-liang3

(1.College of Resource and Environment, University of Chinese Academy of Sciences, Beijing 100049, China; 2. Transportation Institute, Shijiazhuang Tiedao University, Shijiazhuang 050043; 3.Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences/Key Laboratory of Non-point Source Pollution Control, Ministry of Agriculture, Beijing 100081)

To minimum the error of radar rainfall evaluation, an improved Kalman filter method was presented to calibrate the radar quantitative rainfall estimation (QRE). Firstly, the G/R (rain gauge rain rate/radar rain rate) calibration factor model was established. Secondly, the prediction and measurement system of G/R was set up based on the Kalman filter (KF). The calibration process of system parameters and adaptive estimation process of system error was introduced to adjust the parameters of KF dynamically. Thirdly, the G/R calibration ratio was used to correct radar quantitative rainfall estimation. The radar and rain gauge hourly rain data of two rain cases on 2015-08-19-20 and 2016-08-06-07 from Changchun were used to test the efficiency of the proposed method. The results showed that the QRE result with KF calibration was better than that without calibration. And the average relative errors of two rain cases were reduced from 0.6047 to 0.3557 and 0.2645, from 0.8052 to 0.3096 and 0.1715 by ordinary KF and improved KF respectively. Moreover, the improved KF was even better than the ordinary KF.

G/R ratio; Improved Kalman filter; Quantitative rainfall estimation; Adaptive estimation

10.3969/j.issn.1000-6362.2017.07.003

曲小康,芮小平,于雪涛,等.基于改进卡尔曼滤波算法的雷达定量降雨估算[J].中国农业气象,2017,38(7):417-425

2016-11-24

。E-mail：ruixpsz@163.com

河北省自然科学基金“京津冀地区强对流天气下多场因子驱动的风暴体外推方法研究”（D2016210008）；河北省社会科学基金“京津冀地区强对流天气预警及应对策略研究”（HB15SH015）

曲小康（1989-），硕士，研究方向为基于地理信息系统的气象预警方法。E-mail：qxkang@126.com