ROV水下对接液压飞头过程的位姿控制方法研究

程友祥+叶天源+宋琦+谭西都+刘晨曦

摘要：ROV位姿控制的快速性与稳定性是MQC（液压飞头）水下对接成功的关键。本文针对MQC水下对接过程中，海流推力、对接反力等外扰巨大且无法预估的问题，提出了机械臂辅助下的ROV位姿控制的系统结构与工作原理，并在此基础上分析比较了Z-N整定法和模糊算法等PID控制参数优化方法，仿真结果表明，集模糊算法、Z-N整定法于一体的模糊-PID控制算法可以最大限度地提高ROV位姿控制性能，提高MQC水下对接稳定性，提高水下对接成功率。

关键词：MQC对接，ROV位姿控制，Z-N整定，模糊算法，模糊-PID控制

0 引言

MQC（液压飞头）是用来在水下同时连接多个接头的装置，主要用以分配水下液压控制信号。MQC对接是由ROV将移动端与海底设备上的固定端对接，从而实现管路的连通[1]。在MQC对接过程中，ROV位姿控制非常重要。

1 结构与工作原理

ROV是有缆水下自治机器人，通过推进器合理排布实现前、后、左、右、上浮、下沉运动，其携带如机械手、扭矩工具等作业工具，能够辅助完成复杂的作业任务。

ROV的基座处于浮游状态，即ROV并非固定状态，存在自由度冗余，这使得操作具有更高的灵活性，但也造成了运动学反解的不唯一性；同时，ROV的机械手与ROV本体之间存在动力学耦合，机械手的运动会引起ROV的运动，进而导致机械手末端执行器不能准确地定位，不利于末端轨迹的跟踪控制；另外，ROV工作环境面临诸多未知问题，通常都比较复杂，比如海水的作用力、移动端和固定端对接的相互作用力等等对系统的操作都有很大的影响。这些都大大增加了ROV位姿研究的难度[2]。

2 基于ROV的MQC对接过程

深水环境下的MQC对接，潜水员作业受限，需要借助水下机器人进行操作，利用基于ROV进行MQC对接过程如下：首先母船装载所有对接设备预先定位到对接地点的水面上，并把所有设备输送到水下对接地点，准备进行对接；然后ROV向海底设备移动，机械手上带有的扭矩工具从暂置位上取下MQC移动端；ROV再次移动，携带MQC移动端驶向海底固定设备，到达目标地点后机械手将移动端与固定端对接，完成对接后ROV撤离。若对接过程中ROV姿态发生变动，有可能导致对接失败，甚至引起重大事故。

3 ROV位姿PID控制参数优化方法概述

所谓ROV位姿是指在MQC对接过程中，ROV上各点相对参考坐标系的空间位置，稳定性即ROV受到干扰后能否回到原来姿态的性能。ROV运动位姿控制采用PID控制，PID控制从无到有已经经历了近一个世纪，它结构简单、稳定性能好、可靠性高的优点使其至今依然能得到广泛的应用[3]。PID三个参数需要通过优化使系统获得良好的快速性和稳定性，其优化可以通过不同的控制算法实现，优化目的是降低超调，对干扰做出迅速的响应。ROV位姿控制系统是一个非线性流体动力学的系统，其中的多个状态变量多有耦合，以及系统本身的不确定性和环境的多变性都给控制带来挑战。PID控制参数优化方法有多种，这里介绍PID控制参数的Z-N整定法和模糊算法优化方法。

3.1 PID控制参数的Z-N整定法

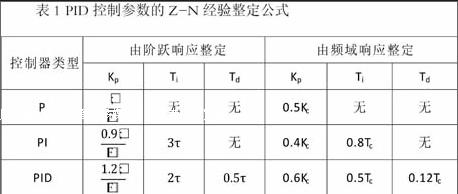
Z-N整定法是Ziegler和Nichols在1942年提出来的PID控制参数的经验整定公式，在实际工业过程中，大多数被控对象获得数学模型后，即可通过时域或频域数据，根据表1所示的Z-N整定经验公式计算PID控制参数。

表1 PID控制参数的Z-N经验整定公式

这里借助MATLAB环境进行整定將会很方便，在得到被控对象传递函数后可以利用MATLAB求得幅值裕量、剪切频率等参数，而后根据上表公式设计PID控制器。但是这样得到的PID控制在面对复杂多变的深水环境时可能得不到预期效果。

3.2 PID控制参数模糊算法优化法

由于PID控制更加适合具有精确数学模型的系统，而实际工业中大多数系统常常比较复杂，再加上深水环境充满了不确定性和未知性，被控对象的参数甚至模型结构都会随之不断发生变化。因此我们希望PID控制器参数最好能够具有自适应性，能够对外界干扰做出快速的反应。于是引入了一个算法——模糊算法。模糊算法是一种根据“相似度”来描述问题的。模糊算法中所有输入变量基于经验值，每个变量对应几个模糊设置，根据从属函数得到解；而抉择逻辑，即模糊规则是自变量和因变量之间的关系，这是基于已有的知识经验；模糊推论则是基于归纳演绎方法；最终得到输出。总而言之，模糊算法针对系统的不确定性和非线性[4]。

一般模糊控制器采用二维模糊输入，其结构框图如图1所示。从中可以看出，输入偏差E和其变化率EC经过量化因子变换后得到模糊论域，然后经过模糊化环节再进行模糊逻辑推理，可以得到输出模糊子集，最后经过解模糊化处理并经过转换，可以得到实际控制量u的输出。这里即采用三个模糊控制器分别对PID控制三个参数进行优化，得到实际的控制参数。模糊算法的稳态性能较好，但会同时牺牲动态性能，降低系统响应快速性。

3.3参数自适应调节模糊-PID控制的参数优化方法

ROV的位姿控制是一个复杂系统，并且外界条件在不断变化，传统的PID控制的控制效果差，如果在被控对象变化的不同阶段采用不同的PID控制就可以实现复杂系统的简单控制。结合深水环境被控对象的特点以及PID控制参数优化方法的优缺点，本文提出了结合Z-N整定法以及模糊算法的方法对PID控制参数进行优化，即模糊-PID控制方法，先通过模糊算法分析偏差和偏差变化率，在线调整PID控制参数——比例系数、积分系数、微分系数的增量，再通过Z-N整定法获得最终优化的参数，实现系统的参数自调节模糊-PID控制。

4 仿真

本文采用MATLAB/Simulink软件进行仿真。仿真模型结构如图2，假设输入信号为一个正弦信号，在2s的时候加入由阶跃信号经过加法器构造的持续时间0.5s的干扰。仿真结果是得到输入信号受到干扰下情况下原被控模型曲线、只经过Z-N整定后的模型曲线、只经过模糊算法优化后的模型曲线和经过模糊-PID控制方法优化后的模型曲线，通过对比上升时间和超调来比较快速性和稳定性，从而得出MQC对接中ROV位姿PID控制参数优化的最优方法。

首先利用MATLAB得到开环传递函数的幅值裕量和剪切频率等参数，再根据表1求得Z-N整定后的PID控制器的比例系数、积分系数和微分系数，然后在simulink子系统里建立Z-N整定后的PID控制器，如图3，可获得只有Z-N整定PID控制的模型曲线。

而模糊算法子系统中的模糊控制结构如图4，比例系数、积分系数、微分系数各有一个调节器，并设计合理的模糊语言变量，制定模糊规则，最终得到三个参数的增量，再经过解模糊可以得到最终的输出，得到模糊算法优化后的模型曲线。若同时结合Z-N整定法，则还要与Z-N整定后PID控制器的三个参数累计求和，如图5，最后解模糊得到实际输出，得到模糊-PID控制优化后的模型曲线。

最终得到如图6所示结果图。在2s中加入阶跃信号干扰后，Z-N整定后的PID控制模型响应速度很快，但是超调很大，稳定性能不好，而加入模糊算法的两种模型则具有很小的超调量，约为Z-N整定模型的10%，稳定性能很好，只是响应速度较慢，牺牲了部分动态性能。而只有模糊算法的模型和模糊-PID控制模型相比，模糊-PID控制模型具有更好的稳定性。

综上所述，模糊-PID控制优化算法可以使模型受到干扰后，以较快地速度响应并具有很好的稳定性，是几种算法中的最优方法，符合MQC对接过程中ROV位姿控制的要求。

5 结论

本文介绍了基于ROV的MQC对接过程，分析了对接过程中ROV位姿控制的重要性，并介绍了几种ROV的PID控制參数优化的方法，分析比较了其优缺点，最终提出了一种参数自适应调节模糊-PID控制方法，理论上能够实现在复杂多变的深水环境中，较快速地优化PID控制参数，并具有很好的稳定性，使得ROV在受到干扰后能够快速而稳定地做出最优响应，从而完成MQC对接作业。

参考文献：

[1]王凤云，刘立新等. 水下多功能液压快速接头的研究概述[J]， 机械工程师， 2015.3（5）：143–146.

[2]徐长密. 水下机器人-机械手系统动力学建模及运动控制研究[D].山东：中国海洋大学，2010.

[3]石振华. PID的自整定控制及其研究[D].内蒙古：内蒙古科技大学，2008. .

[4]J. M. Larrazabal and M. S. Peňas， “Intelligent rudder control of an unmanned surface vessel，” Expert Syst. Appl.， vol. 55， pp. 106–117， 2016.