受损钢结构稳定性研究综述
张曙光,赵丽芝
(1.长春工程学院土木工程学院; 2.吉林省土木工程抗震减灾重点实验室,长春130012)
受损钢结构稳定性研究综述
张曙光1,2,赵丽芝1
(1.长春工程学院土木工程学院; 2.吉林省土木工程抗震减灾重点实验室,长春130012)
在既有钢结构中,有许多结构在地震、腐蚀等因素下受到了不同程度的损伤,这些损伤造成钢材的屈服强度、极限强度、伸长率、屈强比等力学性能指标发生变化,并且严重影响了钢结构的稳定性能。从损伤模型建立、稳定性分析方法、稳定性判别依据3个方面综述了受损钢结构稳定性研究的进展。
损伤;钢结构;稳定性
0 引言
随着我国经济的快速发展,在高层和超高层房屋、大跨度会展中心、轻型钢结构厂房等工程中,钢结构已经得到广泛的应用[1]。然而,在钢结构迅猛发展的同时,因钢结构损伤导致的工程事故时有发生,不仅造成了经济上的损失,甚至造成了人员伤亡,因此,受损钢结构能否满足承载能力的要求一直是人们所关注的问题。钢结构的强度高、韧性好的特性,使得钢结构的稳定性成为一个突出问题。本文从损伤模型建立、稳定性分析方法、稳定性判别依据3个方面综述了受损钢结构稳定性研究进展。
1 国内外钢结构损伤研究现状
早在1847年,德国学者A.Wohler就开始研究金属的疲劳损伤,并在1871年发表了关于循环应力与疲劳寿命的论文;C.Zener在1944年首次将金属材料和裂纹发展的力学性建立起联系,对金属材料损伤进行了进一步研究;Lemaitre[2]于20世纪70年代根据热力学以及连续介质力学理论,研究了不同损伤程度金属材料的受力性能。近年来,Shastry等在美国进行了3个点4种钢16年的暴露试验,得出腐蚀造成钢结构损伤程度的相关结论;Bai等分析均匀腐蚀损伤对导管架平台结构极限强度及可靠性能的影响;Diaye A等借有限元方法研究了节点损伤对局部应力强度因子的变化规律。
我国对受损钢结构研究的起步较晚,近年来国内一些学者为了让自己在受损结构方面的研究更加完善,除参照各种标准规范外,还对损伤钢结构问题进行了专题研究,并取得了的一定的成果,如:班慧勇[3]对为鸟巢而研发的Q460高强度钢进行实验,深入研究受损钢材性能。杜文风等[4]考虑到损伤的累积效应,建立了考虑累积损伤本构关系的模型钢。易贤仁[5]通过对遭受火灾的钢结构材料性能的分析,对钢结构构件在火灾后发生的形变以及残骸等从材料的力学性能、结构构件的承载能力等方面进行阐述并且进一步分析了受损构件的性能。沈祖炎等[6]使用计算机模拟钢构件的滞回曲线,通过这种数值分析方法建立了钢结构恢复模型,此模型综合考虑了损伤累计和断裂效应。李元齐和袁艳敏[7]通过对现有建筑钢结构的可靠性评估方法的研究,提出了有限健康检测等结构的可靠性评估思路。
到目前为止,国内在这方面的研究都有一定的针对性,没有一个全面适用的评估方法,因此,如何确定一个统一全面的评估方法是当前需要我们解决的问题。
2 损伤模型
通常用损伤变量D来描述结构或构件的损伤程度。损伤变量D的范围在[0,1]之间,当D=0时,称为无损状态,当D=1时,说明结构或构件完全破坏[8];损伤变量D是单调递增的函数,结构损伤往增大的方向发展,并且是不可逆的[9]。
损伤分析的方法有很多,引起损伤的因素多种多样,但人们主要都从这3方面入手的:材料退化、变形、变形和能量综合考虑。
2.1 材料退化方面考虑
下面分别从强度退化、刚度退化及每次循环滞回能量的退化来考虑材料退化对损伤变量的影响。
Hearn和Testa[10]认为可以用截面面积的减少来计算损伤变量,即

(1)
(2)
若截面内所有钢材均未达到强化阶段,那么此结构或构件的弹性模量最多下降54.126%,此时,需引入损伤放大因子η=1/54.126%,使整个截面发生最大程度损伤时截面的损伤指标值D=1,由此损伤变量定义为
(3)
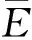
Krawinkler和Zohrei[12]通过试验对钢构件的损伤进行了进一步研究,由试验可知试件的强度、刚度以及滞回能量不断退化,由此定义的损伤模量为
Δdi=A(θpi)α,
(4)
(5)
式中:Δdi为每半个周期循环产生的损伤;δpi为每半个周期循环构件顶部所产生的位移;θpi为每半周期循环的转角范围,θpi=δpi/H;D为循环产生的总损伤;H为构件的长度;A,α为材料常数。
2.2 变形方面考虑
这里所指变形包括构件应变、变形及塑性率等,涵盖范围十分广泛。
Powell 和Allahabadi[13]认为在所有的分析方法中,通过变形得出的损伤指标不仅简单,而且是最为合理的。
山田稔等人对单质点体系的振动进行研究,采用以下3种方法来评价:
方法1:
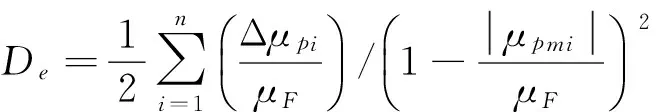
(6)
方法2:

(7)
方法3:
(8)
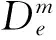
此方法同时考虑了最大变形和循环变形对单质点体系塑性变形产生损伤的影响,是考虑比较全面的损伤模型。
2.3 变形和能量方面综合考虑
欧进萍等[14]首次提出针对钢结构的损伤模型,选用此模型计算结构损伤变量的公式为
(9)
式中:Xu和Xm分别为结构的极限位移和结构在荷载作用下结构的最大层间位移;Eu和Eh分别为结构的极限滞回耗能和结构在荷载作用下的最大滞回耗能。
Biggs[15]和Kato等[16]人最早提出能量和变形双控的概念,但没有给出具体模型;Park等[17]人在此概念的基础上,通过能量和变形线性的组合来描述损伤,具体模型如下
(10)
式中:δm为结构在实际荷载作用下产生的最大变形;δn为结构在单调荷载作用下产生的极限变形;Qy为屈服强度;β为非负参数;dE为吸收滞回能的增量。
Usami[18]对以上模型进行了改进,改进模型为
(11)
该方法综合考虑了结构最大变形和加载历史的影响,因此在损伤分析中有重要意义,只是参数c和β较难确定。此外,该模型有一定的局限性,比如,该模型只适用于理想弹塑性体,并且设定了损伤门坎值为δy,也就是只有当δm大于δy时,该模型才能够反应出损伤累计的特点。
3 稳定性分析方法
3.1 钢结构失稳的分类
3.1.1 平衡分岔失稳
平衡分岔失稳(又称第一类失稳)的特点是构件在受到荷载作用后,其荷载位移曲线并非只有一条路径,而是在达到极限荷载后出现两个可能的平衡途径。不是所有的平衡分岔失稳都是不稳定的,当结构达到极限荷载后,若荷载位移曲线中的一条平衡路径呈现出正刚度,那么此时的平衡分岔失稳为稳定分岔失稳。理想的轴心受压构件和受弯构件等的失稳都属于稳定分岔失稳。
3.1.2 极值点失稳
极值点失稳(又称第二类失稳)的特点是受压构件的荷载—挠度曲线只有极值点,不存在像理想受压构件那样荷载位移曲线在同一点出现两种不同变形状态的情况[19],偏心受压构件以及双向受弯构件等都容易发生此类失稳。
3.1.3 跃越失稳
跃越失稳常见于大跨度结构,其特点是荷载挠度曲线呈现出上升,下降,再上升,甚至一直上升的趋势。后一个上升段结构虽然是稳定的,但此时结构己经被破坏,构件不能继续被利用。两端铰接较平坦的拱结构及扁平的网壳结构都属于这类失稳。
3.2 钢结构失稳的计算方法
由于稳定计算问题属于几何非线性问题,因此与普通结构力学中的内力计算不同,结构力学中的内力计算与结构变形无关,属于一阶分析方法;稳定计算一般是在结构产生微小变形后进行分析,采用的是二阶分析方法。理论计算方法主要包括以下两种:
1)平衡法。平衡法是在结构产生了微小变形后,建立此变形状态下的平衡方程并求解,如果得到的平衡方程的解不只一个,应取其中的最小值作为该结构的分岔屈曲荷载[19]。一般情况下,采用平衡法可以获得精确解。
2)能量法。能量法是首先计算出有了微小变形后结构的总势能,然后根据势能驻值原理对总势能求位移的一阶变分,令一阶变分等于0可以得到平衡方程,与平衡法同理,对平衡方程求解即可得到结构的分岔屈曲荷载。
此外,在实际工程中,很多复杂的问题无法给出精确的解析解,这时就需要采用数值分析方法来解答这类问题。常见的数值解法主要包括有限单元法、等等。有限元法是首先把结构或构件离散成单元,对单元进行分析后再对单元进行整合,可以解决有限差分法及有限积分法不能解决的复杂问题,是目前适应性最强、应用最广泛的解析法,随着计算机的普及,有限元法更是得到越来越广泛的应用[19],目前常用的有限元分析软件有SAP2000、ETABS、ABACUS、ANSYS等。
4 稳定性判别依据
4.1 理论计算方法稳定性依据
4.1.1 完善力学模型的稳定分析
完善力学模型是指理想的、没有初始缺陷的力学模型。以弹簧铰悬臂钢压杆为例来说明此类模型弹性稳定问题。
图1(a)为一在下端是弹簧铰的单自由度悬臂刚性杆,杆的长度为l,弹簧铰的弹簧常数为r,上端作用一铅垂压力P。

图1 弹簧铰悬臂杆
首先计算出变形体(带有弹簧的刚性杆)的总势能
(12)
式中:U为弹簧铰的应变能;V为荷载的势能。

Plsinθ-rθ=0。
(13)
杆的直线平衡状态的稳定性是通过总势能对位移的二阶变分来判断的,若总势能的二阶变分大于0,说明杆件处于平衡状态;若二阶变分小于0,则说明杆件已经失稳,即
(14)
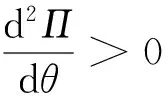
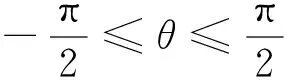
(15)
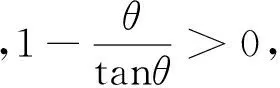
(16)
4.1.2 不完善力学模型的稳定分析
非完善力学模型分析的目的是考察几何缺陷对结构稳定性的影响,同样以弹簧铰悬臂钢压杆为例来说明此类模型的稳定性判别。
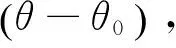
(17)
式中:U为弹簧铰的应变能;V为荷载的势能。
仍然是通过总势能的二阶微分来进一步考察缺陷对杆的影响,即
(18)
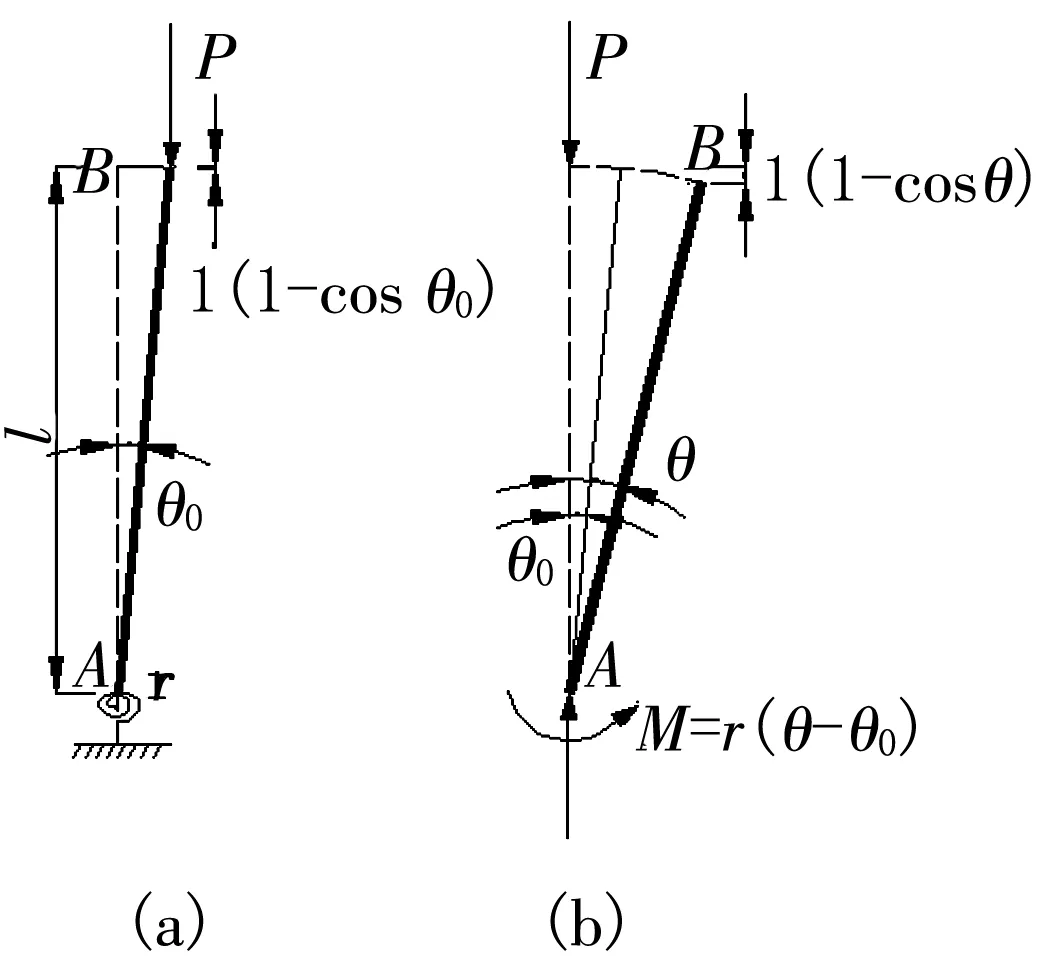
图2 非完善弹簧铰悬臂杆
4.2 结构响应失稳判别依据
目前,国内越来越多的学者对大跨度结构(网壳结构)进行动力稳定性及抗震性能研究。他们通过对结构在地震作用下的时程响应动力稳定性的分析,得到了3类框架失稳判别依据:
1)时域稳定判据。框架结构在输出过程中受外来干扰后,瞬态响应(位移和时间)会逐渐衰减,甚至随时间消失或连续不断,这种情况下的单层框架是稳定的。相反,如果在某一点的输出结构瞬态响应突然增加,呈现出逐渐发散,那么此时的单层框架系统是不稳定性系统。
2)相平面轨迹稳定判据。如果框架结构受到地震作用后,相平面上各个相轨迹环中的相轨迹状态点均做顺时针运动[20],那么框架体系是稳定的;相反,若在某个时间点相平面点的状态突然从环形运动顺时针方向脱开,出现“拐点”并且呈现逐渐发散的趋势,此时,结构体系是不稳定的。
3)能量稳定判据。如果地震作用下的框架结构具有随着时间的增加,滞回耗能、阻尼耗能和动能均按一定的规律呈现出增加的现象,此时,结构体系是稳定的;相反,如果随着时间的增加,在某个时刻滞回耗能突然显著降低,结构自身的动能突然增加[20],能量耗散变得非常混乱,那么,该结构系统是不稳定的。
对于多层结构,有两种类型的动态稳定性判据:一种是特征值屈曲分析,也称为第一类型稳定性分析,是建立在Lyapunov运动稳定性定义与线弹性稳定分析基础上的一种判别方法;另一种是基于双重非线性增量分析与极值理论的极限承载力分析,也称第二类稳定分析。在实际中,第二类型的动力稳定性的应用更加广泛。
5 结语
随着钢结构的使用越来越广泛,钢结构的强度、刚度等各项性能也越来越受到人们的关注。在既有钢结构中,有许多结构在地震、腐蚀等因素下受到不同程度的损伤,这严重影响到了钢结构的各项性能,虽然国内外一些学者根据自己的想法对钢结构损伤问题进行了一些专题研究,但是对于不同程度或者不同位置钢结构损伤的稳定性影响的研究却很少,本文从损伤模型、稳定性分析方法、稳定性判别依据3个方面综述受损钢结构稳定性研究进展,希望能为此方面的研究提供参考。
[1] 李国强,陆烨,何天森.钢结构在现代住宅中的应用[J].工程建设与设计,2005(2):5-11.
[2] 刘华磊.丁家坟滑坡失稳机制及变形预测研究[D].昆明:昆明理工大学,2010.
[3] 班慧勇.高强度钢材轴心受压构件整体稳定性能与设计方法研究[D].北京:清华大学,2012.
[4] 杜文风,高博青,董石麟.考虑损伤累积的单层球面网壳弹塑性动力稳定研究[J].空间结构,2009,15(2):35-38.
[5] 易贤仁.钢结构火灾后的性能分析与鉴定[J].武汉理工大学学报,2005,27(1):54-57.
[6] 沈祖炎,沈苏.高层钢结构考虑损伤累计及裂纹效应的抗震分析[J].同济大学学报,2002,30(4):393-398.
[7] 李元齐,袁艳敏.既有建筑钢结构可靠性评估方法探讨[J].建筑结构,2009(S1):472-475.
[8] 张菁菁.累积损伤和残余应力对焊接组合厚板钢构件的力学性能的影响[D].北京:北京交通大学,2010.
[9] 陈钱商.构件的地震破坏模型分析[J].山西建筑,2009(7):66-67.
[10]HearnG,TestaRB.Modelanalysisfordamagedetectioninstructures[J].JournalofStructuralEngineering,1991,117(10):3042-3063.
[11] 杨雨薇.受损钢框架结构受力性能研究[D].长沙:中南林业科技大学,2014.
[12]KrawinklerH,ZohreiM.Cumulativedamageinsteelstructuressubjectedtoearthquakegroundmotions[J].ComPutersandStructures,1983,16(1-4):531-541.
[13]PowellGH,AllahabadiR.Seismicdamagepredictionbydeterministicmethods:ConceptandProcedures[J].EarthquakeEngineeringandStructuralDynamics,1988,16:719-734.
[14] 欧进萍,牛荻涛,王光远.多层非线性抗震钢结构的模糊动力可靠性分析与设计[J].地震工程与工程振动,1990,10(4):27-37.
[15]LaiSSP,BiggsJM.Inelasticresponsespectraforaseismicbuildingdesign[J].JournalofStructuralEngineering,1980,106(6):1295-1310.
[16]KatoB,AkiyamaH.Earthquakeresistantdesignforsteelbuilding[C]//Proceedingsofthe6thWorldConferenceonEarthquakeEngineering.NuevaDelhi:WorldConferenceEarthquakeEngineering,1977:2518-2526.
[17]ParkYJ,AngAHS.Mechanisticseismicdamagemodelforreinforcedconcrete[J].JournalofStructuralEngineering,1985,111(4):722-739.
[18]KumarSatish,UsamiT.Damageevaluationinsteelboxcolumnsbycyclicloadingtests[J].JournalofStructuralEngineering,1996,122(6):626-643.
[19] 徐城城.双平臂抱杆的静力和稳定性研究[D].合肥:合肥工业大学,2014.
[20] 刘迎春,张文福,计静.单层框架的动力稳定性判据[J].油气田地面工程,2006,12:33.
The Summary to Research on the Stability of Damaged Steel Structure
ZHANG Shu-guang,et al.
(SchoolofCivilEngineering,ChangchunInstituteofTechnology,Changchun130012,China)
Among the existing steel structures,many have suffered different damages caused by earthquake,corrosion and so on.These damages caused many changes in the mechanical property indexes,such as the steel yield strength,ultimate strength,elongation,yield strength ratio,etc.,and has seriously affected the stability of steel structure.This article makes a summary to the research on the stability of damaged steel structures from three aspects including damage modeling,stability analysis method,stability criteria.At the same time,it provides reference for the research with similar problems.
damage;steel structure;stability
2016-10-29
吉林省自然科学基金项目(20130101050JC)
张曙光(1968-),女(汉),吉林白山,教授,博士 主要研究结构优化设计。
10.3969/j.issn.1009-8984.2017.02.001
TU311.2
A
1009-8984(2017)02-0001-05

