综合图形权值法在滑坡变形预测中的应用研究
王兴科,王 娟
(陕西铁路工程职业技术学院,陕西 渭南 714000)
综合图形权值法在滑坡变形预测中的应用研究
王兴科,王 娟
(陕西铁路工程职业技术学院,陕西 渭南 714000)
为提高滑坡变形的预测精度,首先采用卡尔曼滤波对滑坡的变形数据进行去噪处理,分离出趋势项和误差项,再利用多种单项预测模型对趋势项进行预测,最后利用综合图形法确定组合权值,实现趋势项的组合预测;其次,利用神经网络模型对误差项进行预测,进而得到滑坡变形的预测值。结果表明:半参数卡尔曼滤波的效果最优,并通过组合预测有效地提高了预测精度,达到了对滑坡变形高精度及高稳定性预测的目的,验证了该预测模型的可行性和有效性。
滑坡;变形预测;回归模型;神经网络;综合图形权值法
1 研究背景
滑坡是一种常见的地质灾害,对滑坡的研究具有重要的意义,能很大程度上保障人民的生命财产安全。同时,滑坡的变形是滑坡稳定现状的重要体现,因此对滑坡的变形预测研究,能有效地评价滑坡以后的变形趋势,具有必要性。另外,由于多种环境因素的限制,滑坡变形预测数据中会包含有一定的误差噪声,这给预测效果带来了一定的影响,有必要从滑坡变形数据中剔除误差数据。基于此,已有学者进行了一定的研究,如陈冠宇等[1]利用卡尔曼滤波对高铁的沉降数据进行了去噪处理,并通过实例对比分析,验证了卡尔曼滤波能有效去除监测数据中的误差噪声,去噪处理后能有效提高预测精度;王成等[2]将多种卡尔曼滤波模型应用到GPS监测数据的去噪过程中,验证了半参数模型的去噪效果最优,能最大程度上去除误差信息。上述实例研究证明卡尔曼滤波能有效剔除监测数据中的误差信息,因此本文采用卡尔曼滤波对滑坡的变形数据进行去噪处理,进而分离趋势项和误差项。
在滑坡的变形预测方面,也有许多学者进行了研究,如魏小楠[3]、王秀丽等[4]将回归预测模型应用到滑坡的变形预测过程中,并结合实例验证了回归预测模型在滑坡变形预测中的有效性;曹洋兵等[5]则将灰色模型和神经网络模型进行组合,通过滑坡实例验证了该模型的有效性;李秀珍等[6]则建立滑坡变形的多因素预测模型,该模型要优于传统的神经网络模型。同时,也有许多学者将组合预测应用到滑坡的变形预测中,如李秀珍等[7]、隆然等[8]都将不同的组合预测应用到滑坡的组合变形预测中,均取得了良好的预测效果。结合上述成果,本文构建出综合图形法确定的滑坡变形组合预测模型,并将本文模型应用于实例进行研究,探讨其可行性和有效性。
2 研究思路及预测模型的基本原理
2.1 研究思路及创新性
2.1.1 研究思路
本文旨在利用分阶段的多种预测模型对滑坡的变形进行组合预测分析,以期达到提高预测精度和增加预测结果稳定性的目的。本文预测模型的结构如图1所示,其具体思路分述如下:
(1) 采用多种卡尔曼滤波模型,对滑坡的变形数据进行滤波处理,并利用信噪比和均方根误差作为滤波效果评价的基础指标,利用这2个指标进行归一化确定综合指标,选取最优的滤波结果,分解出趋势项和误差项。
(2) 利用多种回归模型和神经网络模型对趋势项数据进行单项预测,并利用本文创新性提出的综合图形法确定组合权值,实现对趋势项的组合预测。
(3) 考虑到误差项的趋势性较差,采用BP神经网络模型对误差项进行预测,得出误差项的预测值。
(4) 基于趋势项和误差项的预测,综合得到滑坡的变形预测结果,最终实现滑坡变形的综合预测。
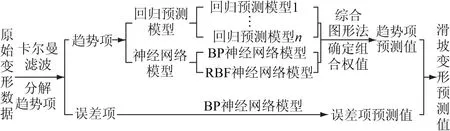
图1 预测模型结构Fig.1 Structure of the prediction model
2.1.2 创新性
在滑坡的变形预测方面,如何提高预测精度和增加结果的稳定性, 是值得深入研究的问题。 同时, 组合预测在实现提高预测精度的同时, 能有效增加预测结果的稳定性, 是一种很好的变形预测方法。 本文的创新性主要是体现在组合预测权值的确定方法上。 以往的组合权值, 都是单一的指标, 如采用误差倒数、 变异系数等, 局限性较明显, 不具有全面性, 而本文基于多种评价指标, 将各指标对应到不同坐标轴上, 进而将各指标确定的图形面积作为本文组合预测模型的综合权值, 即综合图形权值法。 本文预测模型的优势在于能结合多种评价指标的结果, 全面分析单一预测模型的适用性, 为滑坡的组合预测提供了一种新的思路。
2.2 基本原理
结合预测思路和结构,本文所用方法的基本原理如下。
2.2.1 卡尔曼滤波
卡尔曼滤波是一种线性滤波模型,能很好地实现从观测序列中提取出所需信息,进而能够将其应用于去除随机误差信号的过程中,得到有效的实用信息。但是,卡尔曼滤波在应用的推进过程中,易出现发散的现象,且它在粗差的抵抗能力方面具有一定的不足,这说明传统的卡曼滤波具有一定的缺点。因此,本文在卡尔曼滤波的应用过程中,采用了参数修正的方法,建立了多种卡尔曼滤波模型对滑坡的变形数据进行去噪处理。限于文章篇幅,本文对各滤波模型的基本原理不进行赘述,主要的滤波模型包括4种[2],即标准卡尔曼滤波、自适应卡尔曼滤波、抗差自适应卡尔曼滤波和半参数卡尔曼滤波。
同时,对滤波效果的评价也有许多指标,本文选取信噪比和均方根误差作为滤波效果评价的基础指标,并将两指标进行归一化,相加得到综合评价指标,综合指标的表达式为
(1)
式中:L(k)为综合指标;l1(k)为信噪比归一化值;l2(k)为均方根误差归一化值。
2.2.2 单项预测模型
本文的单项预测模型主要包含了回归预测模型和神经网络预测模型,并在两者基础上进一步将预测模型进行细分。其中,回归预测模型共进一步细分了4种模型,即多项式回归模型、指数回归模型、高斯回归模型、幂函数回归模型。利用Matlab拟合工具箱实现上述各模型的预测回归,通过对各模型的预测,得出多项式回归模型中,当多项式阶数大于6阶时,回归方程会产生制约,因此多项式模型共具有6种子模型;其余回归模型均为2种子模型。
在各回归预测模型的回归效果的评价过程中,采用后验差比值作为回归效果的评价指标,其值越小说明回归效果越好,其计算公式为
(2)
式中:C为后验差比值;S1为残差方差的平方根;S2为原始数据方差的平方根。
利用上述后验差比值评价不同回归模型的效果,从4类回归模型中确定出最佳的回归预测模型,将其作为回归预测的结果。同时,将神经网络预测方法引入到滑坡趋势项变形的预测过程中,包括BP神经网络模型和RBF神经网络模型。由于这2种神经网络模型已被广泛地应用和研究,其适用性及原理,本文不再赘述。但在BP神经网络模型的应用过程中,由于隐层节点数对神经网络的预测具有一定的影响[9],因此也采用试算法确定出最优的隐层节点数,并将试算的隐层节点数设置在5~12之间,并以试算样本的累计相对误差值作为评价指标,其值越小,说明节点数越优。另外,考虑到趋势项和误差项都会应用到BP神经网络模型,且已将第19—第25周期样本作为预测样本,因此在试算过程中采用未分解的第14—第18期监测值作为试算验证样本。
2.2.3 组合预测模型
本文组合预测模型采用了基于多种组合指标,以图形方式确定综合值的方式,综合确定出组合权值。同时,也创新性地将Hurst指数引入到组合权值的确定过程中,探讨其适用性。因此,考虑多方面因素,确定组合权值的基础指标共有4个,即误差平方和指标、误差方差指标、Hurst指数指标和后验差比值指标。其中,误差平方和指标是用于评价预测模型的预测精度,其值越小,说明预测效果越好;误差方差指标是用于评价各预测模型残差序列的稳定性,其值越小,说明预测结果的稳定性越好;后验差指标已在前文进行介绍,不再赘述;而Hurst指数是用于评价各序列的趋势性,由于组合预测是用于趋势项的组合预测,且Hurst指数值越接近1,说明预测值的趋势性越好,与本文分解趋势项预测的思路越吻合,限于文章篇幅,其基本原理详见文献[9]。
将上述4个基础指标投影到对应的坐标轴上,考虑到各指标之间的单位具有差异,因此将各指标进行归一化处理,将其归一化值投影到对应坐标轴上,并将各指标在坐标轴上的投影点进行连接,进而确定出指标图形,而该图形的面积即为综合指标的值,具体可见图2。

图2 综合指标确定示意图Fig.2 Schematic diagram of determining comprehensive index

图3 滑坡累计变形Fig.3 Accumulative deformation of landslide
3 实例分析
3.1 工程概况
本文工程实例来源于文献[10],由文献[10]可知,某滑坡位于水利枢纽库的中上段,是库区范围内最大的滑坡体,具有多期、多级的滑动特征,平面上呈扫帚状,主滑方向近似SN向。该滑坡在水库蓄水以来,具有明显的变形特征,通过现场的滑坡变形监测得出滑坡的变形曲线,见图3,共有25个监测周期,且每个周期为40 d。
由滑坡累计变形的趋势图可以得出,滑坡的变形具有持续变形特征,这说明滑坡的变形监测具有其必要性。
3.2 卡尔曼滤波分析
在滑坡变形预测之前,首先采用卡尔曼滤波对滑坡的变形数据进行滤波处理,探讨不同滤波模型在滑坡变形数据中的滤波效果,分解出滑坡变形的趋势项和误差项,为后文预测奠定更好的数据基础。通过滤波处理,得出不同滤波模型的结果,如表1所示。在评价指标的处理过程中,考虑到信噪比与均方根误差具有一定差异,因此在统计过程中,将均方根误差进行倒数处理。由表1可知,半参数卡尔曼滤波的效果最好,其次是自适应卡尔曼滤波和标准卡尔曼滤波,最差的是抗差自适应卡尔曼滤波。因此,选择半参数卡尔曼滤波的结果作为趋势项与误差项分离的依据。
3.3 趋势项单项预测
依据第2.1.1节的研究思路,本文的趋势项单项预测模型包含了回归预测和神经网络预测,回归预测有多项式函数、指数函数、高斯函数、幂函数共4类12种模型,神经网络共有2种模型。
多项式函数表达式为

(1)
式中i为阶数。
指数函数表达式为
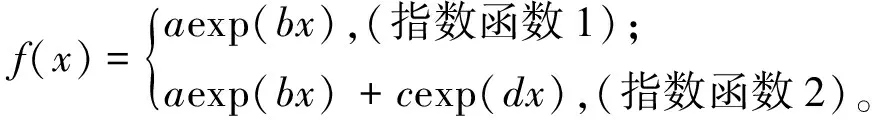
(2)
高斯函数的表达式为
(3)
幂函数的表达式为
(4)
3.3.1 单项回归预测
在滑坡变形趋势项的预测过程中,本文采用了多项式回归模型、指数回归模型、高斯回归模型及幂函数回归模型对滑坡的趋势项进行回归预测,并以后验差指标评价回归效果,结果如表2所示。
分析表2可知,不同模型的回归效果具有一定差异性,在多项式回归模型中,随多项式阶数的增加,回归效果越来越好,以6阶多项式回归的效果最优,其余模型均以模型2的回归效果最佳。进而选取4种模型中最优的回归子模型作为本文回归预测的结果,并将相关模型的表达式进行统计,结果如表3所示。

表2 回归预测成果统计

表3 最优回归模型的表达式统计
3.3.2 神经网络预测
根据对BP神经网络不同隐层节点的试算,得出不同隐层节点数的误差统计,如表4所示。

表4 隐层节点误差统计
通过对不同隐层节点的试算,得出不同隐层节点对BP神经网络的预测效果的确具有较大的影响,也进一步验证了对隐层节点进行试算,确定出最优隐层节点数的必要性。同时,在本文实例的试算过程中,节点数为10时的误差最小。因此,确定出BP神经网络的隐层节点数为10。
以第19—第25周期的变形数据作为预测样本,通过BP神经网络模型和RBF神经网络模型对滑坡变形趋势项的预测,结果如表5所示。

表5 神经网络预测结果统计
通过神经网络预测得出不同类型的神经网络模型在本文实例变形预测中的效果也具有一定差异,说明不同模型的适用性和有效性是有差异的。通过后文组合预测,能有效降低误差不确定性的风险,验证了本文组合预测思路的有效性。
同时,通过对比不同节点处的相对误差,得出两预测模型预测结果的起伏变化较大,差异也较为明显。BP神经网络模型的最大相对误差为2.21%,最小相对误差为1.67%,平均为2.02%;而RBF神经网络模型的最大相对误差为2.66%,最小相对误差为1.49%,平均为2.19%,且BP神经网络模型较RBF神经网络模型具有更好的稳定性。
3.4 趋势项组合预测
单项预测结果已为组合预测提供了基础数据。结合本文组合预测思路,进一步求解各单项预测模型的组合权值,具体结果如表6所示。
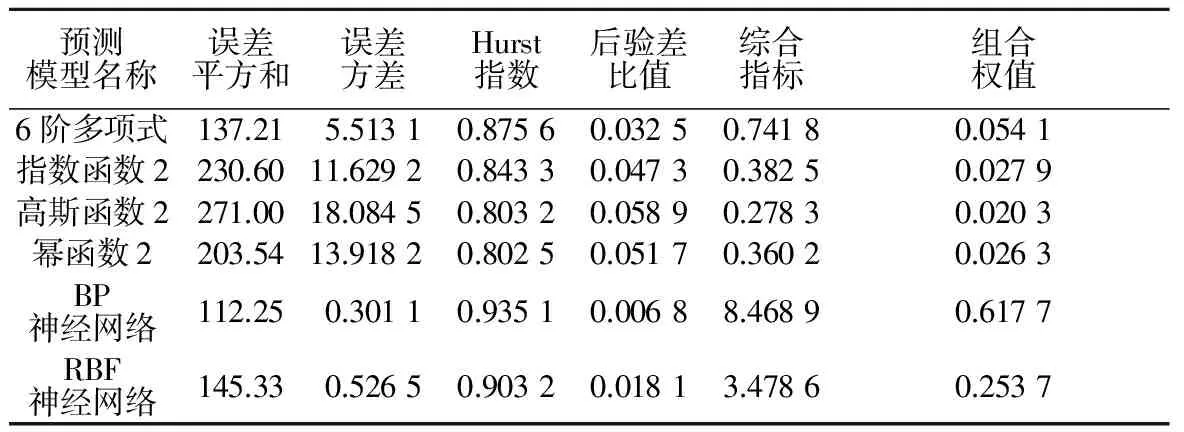
表6 组合基础指标及其权值
通过分析不同预测模型的组合权值可以得出,回归预测模型在本文实例中的预测效果不及神经网络模型,其中,组合权值最大的是BP神经网络模型,其次是RBF神经网络模型,而其他类型的回归预测模型的组合权值基本相当。通过组合预测,得到趋势项的预测结果如表7所示。

表7 趋势项的预测结果
通过统计,得出趋势项组合预测结果的相对误差平均值为1.79%,方差为0.121 5,对比单一预测模型的相对误差及其对应方差,组合预测均在预测精度及结果的稳定性上均有了一定的提高,说明了本文组合预测的有效性和可行性。
3.5 误差项预测
考虑到误差项的随机性,采用BP神经网络对其进行预测,预测结果如表8所示。通过对误差项的预测,得出误差项预测相对误差的平均值为4.86%,方差为1.117 7,相较于趋势项的相对误差结果,误差项的预测精度及稳定性均较差,说明误差项的随机性要大于趋势项的随机性,从侧面验证了本文实现了趋势项与误差项的有效分离,证明了预测模型和思路的有效性和可行性。
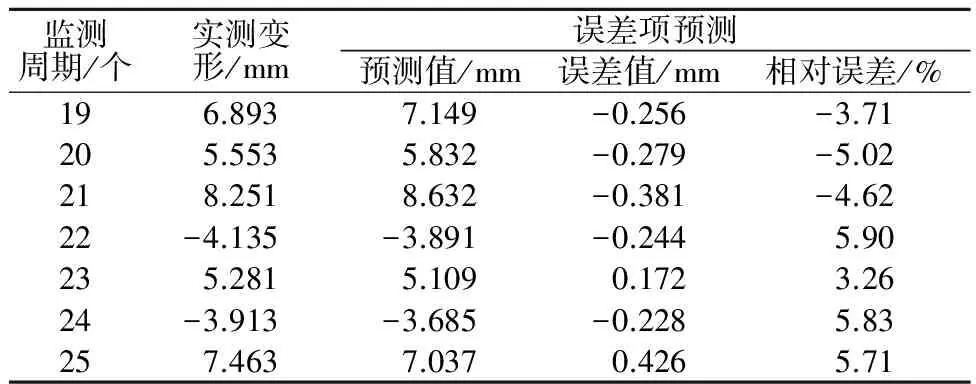
表8 误差项预测结果
通过前文的趋势项及误差项的预测,将两者进行组合,得到综合预测结果如表9所示。

表9 综合预测结果统计
通过综合预测,得到滑坡变形预测值的最大相对误差为2.17%,最小相对误差为1.31%,相对误差的平均值为1.69%,方差为0.104 6。进一步对比趋势项及误差项的预测结果可知,综合预测的精度及稳定性均有提高。
通过滑坡变形分离组合预测,将图形指标权值法引入到滑坡的组合变形预测中,有效地提高了滑坡的预测精度及预测结果的稳定性,验证了预测方法及思路的有效性。
4 结 论
(1) 通过不同类型滤波方法在本文滑坡变形数据中的应用研究,得出半参数卡尔曼滤波的滤波效果最佳,并将其应用于变形数据的滤波处理中,分离出趋势项与误差项。
(2) 在单项预测模型的预测过程中,神经网络的预测效果要优于回归预测模型的预测效果。
(3) 通过对趋势项的组合预测可知,综合预测相对误差的平均值为1.69%,有效提高了预测精度及结果的稳定性,验证了预测思路的有效性。
通过图形权值法确定了组合预测的权值,但采取的是统一归一化处理的方式,未对各评价指标的贡献率进行评价,故这方面仍需进一步的研究。
[1] 陈冠宇,文鸿雁,周 吕,等. 基于Kalman滤波下的高铁隧道沉降变形评估方法[J]. 桂林理工大学学报,2013,33(4):671-676.
[2] 王 成,何美琳,覃 婕,等. 半参数Kalman滤波模型在GPS变形数据处理中的应用[J]. 施工技术,2015,44(增刊):818-821.
[3] 魏小楠. 曲线回归分析模型在滑坡预测中的应用[J]. 华东公路,2008,(3):65-67.
[4] 王秀丽,李恒凯. 滑坡变形的回归-神经网络预测模型研究[J]. 人民黄河,2012,34(7):90-92.
[5] 曹洋兵,晏鄂川,谢良甫. 考虑环境变量作用的滑坡变形动态灰色-进化神经网络预测研究[J]. 岩土力学,2012,33(3):848-852.
[6] 李秀珍,王芳其. 滑坡变形的多因素小波神经网络预测模型[J]. 水土保持通报,2012,32(5):235-238.
[7] 李秀珍,王成华,孔纪名. 基于最优加权组合模型及高斯-牛顿法的滑坡变形预测研究[J]. 工程地质学报,2009,17(4):538-544.
[8] 隆 然,董志勇. 基于小波去噪和神经网络的滑坡变形组合预测研究[J]. 路基工程,2015,(6):33-39.
[9] 罗 林,左昌群,赵 连,等. 基于BP神经网络和R/S分析的隧道仰坡沉降变形预报预测[J]. 施工技术,2014,(11):80-84.
[10]秦 鹏,张喆瑜,秦植海,等. 滑坡体监测数据的改进变维分形-人工神经网络耦合预测模型[J]. 长江科学院院报,2012,29(3):29-34.
(编辑:黄 玲)
Application of Comprehensive Graph Weight Method toLandslide Deformation Prediction
WANG Xing-ke,WANG Juan
(Shaanxi Railway Institute,Weinan 714000,China)
The aim of this research is to improve the accuracy of predicting landslide deformation. Firstly, trend
terms and error terms were isolated through denoising the deformation data by using Kalman filter. Then comprehensive graph weight method was employed to determine the combinatorial weights for trend terms. Furthermore, neural network model was adopted to the prediction for error terms. Results suggest that the effect of half parameters and half Kalman filter method is the optimum. The present model has improved prediction accuracy, and is verified to be of feasibility.
landslide; deformation prediction; regression model; neural network; comprehensive graphic weight method
2016-07-07;
2016-07-31
王兴科(1982-),男,河北石家庄人,讲师,硕士,主要从事土木工程方面的教学与研究工作,(电话)0913-2221326(电子信箱)524980530@qq.com。
10.11988/ckyyb.20160691
2017,34(7):82-86,93
P642.22
A
1001-5485(2017)07-0082-05

