基于星相机的高精度卫星姿态计算算法研究
王 飞
(西安航空学院 飞行器学院,陕西 西安 710077)
基于星相机的高精度卫星姿态计算算法研究
王 飞
(西安航空学院 飞行器学院,陕西 西安 710077)
在航空航天技术的具体应用中,星相机是一种重要的卫星姿态设备,其通过拍摄稳定恒星的图像来获取卫星的高精度姿态信息,从而实现卫星姿态的精确控制。因此,基于星相机的卫星姿态计算算法就成为了星敏感器研究的重要内容。为了实现卫星姿态的高精度计算,文中参考并分析了大量的文献,修改了Top-hat变换,并设计出了一个高可靠度、高精度的卫星姿态计算方法。通过数据实验分析证明,该算法可以用于星点提取,实现了3"~9"的高精度姿态计算。
星相机;卫星姿态计算;Top-hat变换
随着航空航天技术的不断发展,尤其是卫星的分辨率不断提高,无控制点的定位技术成为了卫星遥感技术的热点研究方向[1],而高精度卫星姿态计算是实现卫星无控定位的基础技术。如何利用星相机来精确确定卫星姿态便成为了一个重要的问题。
由于航空航天技术的需求[2-3],星相机也被称作星敏感器,其被发明的目的是实时精确测量恒星的张角。而随着探测技术和微处理器的更新,新一代的星相机可实时识别星图,并成为了计算卫星姿态的基本器件[9-12]。
本文基于新一代的星相机,为了能够以高精度的标准实时计算卫星姿态信息,提出了一套可行且可靠的计算方法,其方法主要包括5个方面:(1)通过改进的Top-hat变换,获得初始星点图,再通过形态学和联通域检测来去除伪星点,从而准确得到星点图;(2)计算星点图的背景梯度,得到梯度阈值,由聚类分析等方法划定星斑的范围;(3)用平方加权质心法进行星点质心定位,从而获得图中星点的质心坐标;(4)用三角形匹配的方法得到星点的天球坐标;(5)用迭代的方法计算出最终的卫星姿态数据。
1 星相机概述
星相机技术的发展阶段可以分成早期、非自主星相机和自主星相机阶段。从1940年到1970年代,早期的星相机主要使用析象管作为探测器件。从1970年至1990年代,非自主星相机使用电荷耦合器件(CCD)做探测器件,大幅提高了星相机的性能,这一代的星相机视场比较小,只能跟踪较高星等的恒星,跟踪星数少,没有自主识别星图能力,仅能获得角距信息[13-16]。从1990年代至今,微处理技术和大容量存储技术有了较大的进步和应用。尤其是CMOS APS技术的成熟,使得星相机可以存储整个导航星表,全天24小时覆盖导航星,实现了星图自主识别。这一阶段的星相机技术已经成熟,能够直接得出姿态信息。
2 创建导航星表
首先,创建导航星表需要筛选导航星,这样做的目的在于保持星图识别率的同时,令导航星尽量的少,减少星相机的存储空间,同时提高识别星图的效率。具体而言,导航星数目n越大,姿态计算精度e会越高,通常n≥6。令e0为单颗星的姿态计算精度,则姿态计算精度e与导航星数目n的关系为
此外,选取导航星时应尽量保证在视场中均匀,剔除双星和变星等情况,令星等阈值为6.95 Vmag,在每个视场里将导航星个数阈值设置为16,选取2 751颗恒星,组成导航星表。在实际应用中,星表的快速检索能力严重影响了星图识别,所以需要将全视场分成若干个小块。文中用赤经赤纬法来划分全视场,该方法是使用等间隔的赤经和赤纬将全视场分成经纬网格,这种方法简便易行,可改善检索效率。
3 恒星视位置转换
恒星视位置是在某一特定时刻相对于地球质心的恒星位置,由恒星历元平位置经过改正获得的视位置,其中包括自行、岁差、章动和光行差等改正。这些改正中由不同历元的平赤道坐标系引起变化的原因是岁差;而同一历元的真赤道坐标系和平赤道坐标系差异的原因是章动;若恒星的观测历元和坐标系的定向历元不同,实际操作中还需要对恒星自行改正;因为恒星的视位置的定义,文中还需要对周年光行差进行改正。
4 星点提取、定位和匹配
4.1 新型Top-hat变换
新型Top-hat变换利用了目标与周围的差异,比原来的Top-hat变换拥有更强的目标检测能力,其噪声和背景影响效果更小。新型Top-hat变换的闭运算和生态学开运算为
(f·Boi)(x)=[(f⊕ΔB)ΘBb](x)
(f°Boi)(x)=[(fΘΔB)⊕Bb](x)
式中,将两个扁平结构元素表示为Bi和Bo, 的直径>Bi,ΔB=Bo-Bi,Bb的直径位于Bi和Bo之间,Bb是Bi和Bo形状相同的扁平结构元素。
新型Top-hat变换可被定义为
NWTH(x,y)=max(f(x,y)-(f·Boi)(x,y))
NBTH(x,y)=max((f°Boi)(x,y)-f(x,y))
4.2 星斑确定和联通域检测
经过新型Top-hat变换可判断出星点的存在性,基于梯度和聚类分析可以确定星斑范围,其方法描述如下:
(1)寻找星斑内灰度值最高的像素,将该像素当做内层数据;
(2)用内层数据和周围外层数据来计算梯度值;
(3)若这些梯度值中75%的值大于背景梯度,则将这些外层数据作为可能星斑范围值;
(4)计算外层和内层数据的灰度差CS,并计算背景值和外层数据的灰度差CB,CB (5)循环运行步骤(2)~步骤(4),在步骤(3)判断为否时执行步骤(4),结束循环。 用闭运算获得的背景影像可以计算背景阈值T,用阈值可以将图像二值处理。其中,连通域的搜索和标记是目标提取,本文使用了基于线扫描的连通域搜索算法: 1)首先,扫描一组数据; 2)记录下这组数据的所有黑段信息; 3)扫描下一组数据,记录下这组数据的所有黑段信息; 4)比较前后两组黑段信息,如果交集非空,则将第二组黑段信息的编号赋给第一组黑段信息。若有若干个交集,则将编号均赋给第一组的第一个有交集的黑段信息编号。 4.3 星点定位 文中使用带阈值的平方加权质心法,其模型的表达式为 式中,(μ0,v0)是星点质心坐标;μi是质心数据的行号;vj是计算数据的列号;K=2.0,g(μi,vj)表示灰度值。背景阈值T=μ+mσ,其中,μ是背景影像的均值,σ是均方差。令m=10 4.4 星图匹配 因为三角形匹配方法是最常用的星图匹配方法,所以使用此方法来进行匹配,具体如下: (1)选出若干数量的星,算出这些星之间的角距。恒星的方向矢量 选取两颗恒星,其的角距为 恒星在物方的方向矢量为 (3)如果搜索到三颗星的角距与计算出的结果匹配,则存在s1,s2和s3满足要求; (4)输出匹配结果。 如图所示,星像空间坐标系可以被由此建立。其中o为星像摄影机中心,O′o和星像摄影机的主光轴方向相同,O-XYZ是天球坐标系。图中的相片就是正片的位置,O′o轴线和天球上的赤经α0、赤纬δ0的方向相同,按照右手坐标系的规则,k是正向相片y轴和子午面之间的夹角。 图1 星像空间坐标系的姿态示意图 令S是两个空间坐标系的相互转角关系,则 矩阵S可以由相片空间坐标系旋转3次到天球坐标系得出,用下式表示为 然而 这里A=cos(α)cos(δ),B=sin(α)cos(δ),C=sin(δ)。将主点位移和径向畸变加入方程中,则 所以,按照上式便可得到以下的观测方程式 -vx=s1Δα+s2Δδ+s3+Δk+s4Δx0+s5Δy0+s6Δf+s7Δk1+s8Δk2+s9Δk3+lx -vy=t1Δα+t2Δδ+t3+Δk+t4Δx0+t5Δy0+t6Δf+t7Δk1+t8Δk2+t9Δk3+ly 其中的系数表达式为 s4=-1+(k1r2+k2r4+k3r6) t4=0 s5=0 t5=-1+(k1r2+k2r4+k3r4) s7=-(x-x0)r3t7=-(y-y0)r2 s8=-(x-x0)r4t8=-(y-y0)r4 s9=-(x-x0)r6t9=-(y-y0)r6 因此,按照上式可以得到观测方程式,lx和ly是常数项。相片上的每个像素均能够列出两个观测方程式,所以必须有5颗恒星才能计算出来。实际应用中,每张相片不止有这么多的像素,用最小二乘法就可以计算出卫星的姿态信息。 本文使用双矢量定姿方法确定了初始姿态,通过迭代求解得到了最终姿态,部分的实验最终定姿结果如表1所示。 表1 定姿结果 通过统计上述结果可以看出,俯仰和偏航角优于3",翻滚角优于9",说明本文的算法定姿精度较高。 从星相机被发明至今,国内外的学者提出了大量的星图识别算法,但到目前为止即使是成熟的算法,也均无法满足航空航天技术的需求。因此本文改进了现有算法,尽量去逼近理想的结果,并尽可能地减小计算误差。在未来的研究中,希望能够有更好的算法来解决这一问题。 [1] 林旭.自适应Kalman滤波方法及其在航空矢量重力测量中的应用[D].武汉:武汉大学,2014. [2] 范曹明,王胜利,欧吉坤.GPS/BDS卫星姿态异常对PPP相位缠绕的影响及其改正模型[J].测绘学报,2016,45(10):1165-1170. [3] 赵琳,邱海洋,郝勇.范数有界的鲁棒卫星姿态估计方法[J].华中科技大学学报:自然科学版,2016,44(4):43-47. [4] 徐赫屿,王大轶,李文博.卫星姿态控制系统的可重构性量化评价方法研究[J].航天控制,2016, 34(4):29-35. [5] 马晓萌,李凉海,张振华.一种THz SAR的宽幅、高分辨成像方法研究[J].遥测遥控,2015,36(3):23-29. [6] 路坤锋.空间飞行器姿态复合控制方法研究[D].北京:北京理工大学,2014. [7] 刘磊,刘也,曹建峰,等.一种星敏感器-陀螺组合定姿的实时在轨标定方法[J].飞行器测控学报,2014,33(2):152-157. [8] 雷琦,龚志辉,林雕,等.AEKF在星敏感器低频误差补偿中的应用[J].测绘科学技术学报,2016,33(3):252-257. [9] 张沪玲,黄昆,赵乾宏,等.船载卫星通信地球站三轴稳定天线坐标计算方法改进[J].电讯技术, 2016,56(2):183-189. [10] 孙阳,薛栋林,郑立功,等.基于速度矢量模型的圆轨道空间相机偏流角实时补偿[J].红外与激光工程,2014,43(7):2185-2191. [11] 淡鹏,陈剑平,DANPeng,等.自旋卫星几何定姿限制条件及误差分析[J].电子科技,2016,29(5):62-66. [12] 夏中秋,黄巧林,何红艳,等. 高分辨率光学遥感卫星几何链路定位精度分析[J]. 航天返回与遥感, 2016(3):111-119. [13] 韩晓磊,张庆君,刘杰,等.敏捷SAR卫星聚束模式姿态机动策略研究[J].航天器工程,2016,25(4):13-19. [14] 李迪阳.船载卫星通信地球站中上位机系统的研究与实现[D].南京:南京邮电大学,2016. [15] 杨腾飞.GPS卫星导航信号仿真研究[D].杭州:浙江理工大学,2016. [16] 丰保民,陈占胜,叶立军,等.倾斜轨道小卫星太阳高度角分析与机动方案设计[J].空间控制技术与应用,2016,42(3):33-37. Research on Satellite Attitude Calculation Algorithm Based On Star Camera WANG Fei (School of Aircraft,Xi’an Institute of Aeronautics and Astronautics, Xi’an 710077, China) In the specific application of the aerospace technology, the star camera is an important equipment of satellite attitude, high precision attitude information through image to obtain stable star satellite, so as to realize the accurate control of satellite attitude. Therefore, satellite attitude estimation algorithm based on star camera has become an important part of star sensor. In order to realize the high precision calculation of satellite attitude, this paper introduces and analyzes a large number of literatures, modifies the Top-hat transform, and designs a high reliability and high precision satellite attitude calculation method. A lot of experiments proved that the algorithm can be used for extracting and achieve a high precision attitude (3"~9"). star camera; satellite attitude calculation; Top-hat transform 2017- 03- 01 王飞(1987-),男,硕士,助教。研究方向:飞行器设计,航天器惯性导航。 10.16180/j.cnki.issn1007-7820.2017.08.004 TN927 A 1007-7820(2017)08-013-05
5 姿态计算



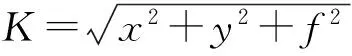


6 实验结果

7 结束语

