基于LASSO回归模型的网贷借款成功影响因素挖掘①
李海超, 王开军
(福建师范大学 数学与计算机科学学院, 福州 350007)
(福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007)
基于LASSO回归模型的网贷借款成功影响因素挖掘①
李海超, 王开军
(福建师范大学 数学与计算机科学学院, 福州 350007)
(福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007)
随着P2P网络借贷交易量的增大, 对P2P交易数据的挖掘和分析备受关注, 其中一项重要的研究课题是网络借款成功率的影响因素分析. 现有的文献多采用线性回归方法对该课题进行研究, 但未考虑变量之间的多重共线性和采用最优变量子集建立回归模型的问题. 本文采用Lasso回归方法, 建立最优变量子集的回归模型对影响网络借款成功率的因素进行分析, 避免了多重共线性问题对模型的干扰, 同时提高了模型对数据的拟合精度. 对Lending Club平台的借贷数据的实证分析结果显示, 本文方法在模型的拟合精度和避免共线性方面优于对比方法.
P2P网络借贷; Lasso回归; 多重共线性; 借款成功率; 借款用途
近年来依托互联网开展交易业务的互联网金融蓬勃兴起, 产生了一种新的金融模式——P2P网络借贷平台, P2P网络借贷平台在英、美等主要发达国家已经相对成熟且被广大人们接受, 如美国的Lending Club、英国的Zopa、中国的拍拍贷和人人贷等. 截至2016年4月仅我国P2P网贷行业累计平台数量就已达4029家, 借贷成功的网贷贷款余额高达几千亿元.
P2P网贷行业经历了几年的发展, 积累了大量的网络借贷交易数据, 对这种新型交易数据的挖掘和分析受到了越来越多的关注, 对网络借款成功率方面的研究是其中一项重要的研究课题. 现有的基于回归模型的研究成果包括: Freedman & Jin[1]在研究中发现, 提供更多的财务信息会使得借款人的借款成功率大大提升;吴小英[2]采用最小二乘法模型对Prosper平台数据进行实证研究表明, 在同等情况下学生借款比其他种借口成功率低3.4%; 陈建中[3]通过个人信息对借款成功率的影响进行实证分析, 结果表明借款人基本信息对借款成功有着显著的影响; 温小霓[4]使用logistic回归模型研究影响借款成功率的因素; 李渊博[5]采用多元线性回归模型对出借人投标行为的影响因子进行研究, 结果表明借入信用、人口特征等对出借人投标行为有显著的影响; 王会娟[6]研究发现, 信用评级越高, 其借款成功率越高; 李明初[7]采用Probit模型探究了显著影响投资人以及网贷平台对于借款判断的因素等. 每笔P2P借贷业务的属性众多, 许多属性之间有一定的相关性, 使得各属性(变量)的数据之间或多或少存在多重共线性. 使用这种具有多重共线性的变量所建立的回归模型, 将导致模型偏差、模型精度降低. 上述文献中, 尚未采用Lasso回归模型来处理多重共线性问题. 本文提出基于Lasso回归方法的借贷成功率模型, 可有效解决数据中存在的多重共线性的问题, 并可以选出更优的具有解释能力的自变量子集建立回归拟合模型等优点, 以提高借款成功率模型的拟合精度.
1 线性回归模型
1.1 最小二乘法的线性回归建模
研究一个因变量与多个自变量之间的相关关系,假设数据(Xi, Yi), 这里Xi=(xi1, xi2, …, xim)T和Yi分别是第i个观测值对应的自变量和因变量, 通常的线性回归模型为[8]:

其中, β0, β1, …, βm为回归系数, m代表有m个自变量,ε代表随机误差. 通常假设ε是服从均值为0, 方差为δ2的高斯分布, 即ε~N(0, δ2), 由此可以利用观测值来进行参数的估计.
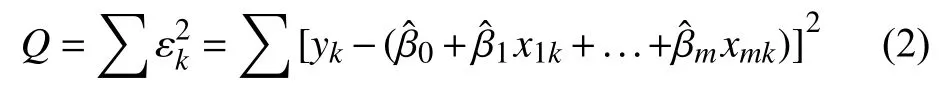
根据最小二乘法求解回归系数, 应使得残差平方和Q达到最小值, 可以分别对上式求偏导, 求出相应的回归系数值. 然而直接用这传统的最小二乘法, 在处理多重共线性问题上往往有很多不足的地方,主要存在两大缺陷[9], 一是预测精度的问题, 最小二乘估计虽是无偏估计, 但其方差在自变量线性相关的程度高时通常较大; 二是模型的可解释性差, 对于很多自变量时情况, 结果不稳定, 我们希望确定一个较小的变量模型来得出最好的效果. 当变量之间存在多重共线性问题时, 用最小二乘法所得到的误差比较大, 不能起到消除共线性和降维效果[10].
1.2 基于Lasso估计方法的线性回归模型
Lasso回归方法[11]的主要思想是在回归系数的绝对值之和小于一个正常数的约束下, 使得残差平方和最小化, 从而能够使得回归系数很小或者为0的变量被筛选掉, 能有效的解决多重共线性的问题. 它具有子集选择的优点, 同时又能进行变量选择与未知参数估计.
在通常的回归结构中, 假设数据中的观测值彼此独立, 同时因为数据中有多个变量, 一般都存在量纲不同的问题, 所以为了消除量纲影响, 我们首先对所有自变量数据进行标准化变换, 即:, 使的均值为0, 方差为1, 且无量纲. 求解回归模型的Lasso估计为:
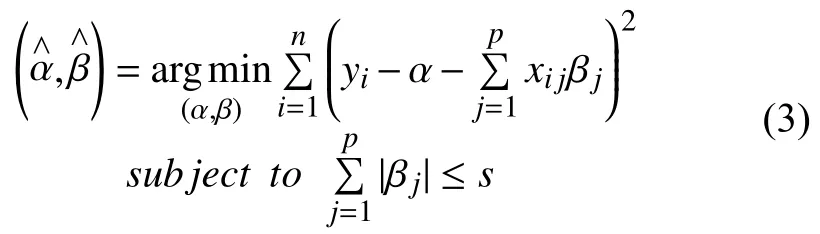
Lasso回归系数的确定可采用Mallows Cp统计量[12],该方法是一种常用来评价回归模型的方法, Cp统计量的定义如下:
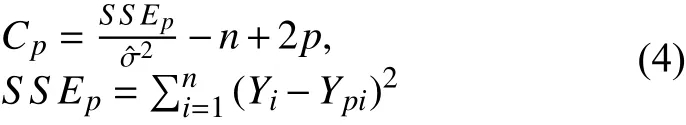
其中, p为子集回归模型中包含的自变量的个数(即入选自变量个数), n为样本容量, SSEp是入选自变量对因变量Y作回归的残差平方和,为全部自变量对因变量Y作回归时, 平均平方误差的估计. 据此, 选取Cp值达到最小时的模型[13], 即选择出了全局“最优”的变量子集,得到最优的回归方程.
因此, 基于Lasso估计方法的线性模型能比较好的进行变量选择, 进而用选择出最优的自变量子集得出最优的回归方程. 同时消除了多重共线性问题和起到降维效果.
2 基于回归模型的借贷成功率分析
本文采用Lending Club平台的数据作为研究样本,其数据包括资金需求、利息率、借标人数、借款成功率、借款用途、月收入、信用评级等属性. 当采用线性回归模型(1), 并在上述1.2节的基础上选择出自变量子集来建立借款成功率模型时, 把借款成功率作为因变量, 资金需求、年利率、利息率、借标人数、信用评级、房屋所有权等属性作为因变量. 然而, 这样并不利于研究各种详细的借款用途对借款成功率是否有影响. 因此, 为了验证各种用途对借款成功率是否影响,借款用途可看成虚拟变量, 在回归模型中常被设计为哑元来处理, 将其表示为β1iPurposei. 为观察自变量Xi=(xi1, xi2, …, xim)与因变量P(P是筹款完成率, 即成功率)之间的关系, 对包含资金需求、利息率、资助金额、借标人数、借款时长等借款属性X(自变量)与因变量P, 作成分残差图[14]; 对包含信用评级、月收入、房屋所有权、循环信贷余额等借款人属性W(自变量)与因变量P, 也作成分残差图, 该图适用于分析拟合模型中因变量与自变量之间是否呈非线性关系[14]. 观察到自变量X与因变量P之间呈现有近似sin函数的非线性关系, 为使P与X之间的回归模型符合这种非线性关系,将借款成功率模型设计为如下含sin函数的非线性回归模型:
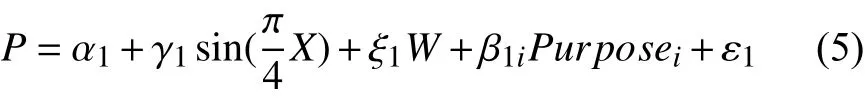
其中, P表示借款成功率, X表示借款属性包括借款金额、利息率等, W表示借款人的属性包括信用评级、房屋所有权等, Purposei为哑元变量, γ1表示借款属性的回归系数, ξ1表示借款人属性的回归系数, β1i为各借款用途的回归系数, ε1表示数学模型的随机误差, ε1~N(0, δ2).
使用公式/模型(5)对Lending Club的数据进行建模分析, 可对各种因素对借款成功率的影响进行分析, 求解时采用Lasso回归求解方法. 这样能有效处理数据的多重共线性的问题, 剔除与借款成功率相关性不大的因素; 也可以得出每种借款用途的系数β1i, 即每种借款用途对借款成功率的影响程度, 等.
3 实验结果与分析
本文的实验是采用Lasso回归的求解方法, 对实验数据采用回归模型(5)进行建模分析每种借款用途对借款成功率的影响, 同时与现有的文献中吴小英[2]、陈建中[3]、李渊博[5]等所采用的普通的最小二乘法求解线性回归方法(即模型(1))进行对比实验. 实验程序是使用R语言编制.
在美国网贷平台Lending Club, 借款人通过在网上填写资料申请借款, 由此产生网络借贷数据. 本文实验数据是Lending Club在2012年里的49737笔有效借贷数据, 每笔借贷样本属性主要包括借款金额、借款用途、借标人数、利息率、年利率、借款时长、资助金额(成功募集)、信用评级、FICO评分、总信用额度、房屋所有权、月收入、债务与收入比率、循环信贷余额、循环信贷利用率、教育程度、地址、工作年限等信息. 将这些有效数据按借款用途对照借款成功人数进行汇总统计, 汇总结果列于图1, 从图中可以看出借款用途为债务巩固、信用卡债务借款成功人数占比比较大, 占成功借款总人数的55.83%、18.87%; 而用于汽车债务、大宗购买债务的仅仅占成功借款总人数的1.73%、1.80%. 从直观上来看, 这表明了Lending Club比较青睐债务巩固和个人债务的借款人, 而对汽车债务和大宗购买这些高费用和还款周期比较长的债务抱有敌视. 直观上看, 借款用途说明了借款人借款的目的, 其必定是作为投资人重要的考量标准, 所以借款用途对借款成功率必有一定的影响. 文将以Lending Club平台数据为基础, 通过其近年来的数据分析研究借款用途对借款成功率的影响.

图1 成功借款中各种借款用途的人数图
实验中把每个变量的数据标准化为均值为0、标准差为1的数据, 信用评级A、B、C设为高信誉, 赋值为1; 信用评级D、E、F为低信誉, 赋值为0. 房屋所有权情况, 租房赋值为0, 抵押赋值为1, 已有赋值为2;FICO评分区间取其平均数, 如FICO值为“679-713”, 则取平均值696; 借款用途共分为七种, 先用0~6这7个数值代表各用途.
对上述Lending Club实验数据, 选取其前三分之二的数据作为训练集用于构建预测模型, 剩余三分之一则作为测试集用于评估预测模型的性能. 本文先对关于借款成功因素的文献[2,5,6]中线性回归方法构建模型(1)进行实验, 用借款成功率作为因变量, 资金需求、资助金额、借款用途、借标人数、利息率、年利率、借款时长、信用评级、房屋所有权、月收入、债务与收入比率、FICO评分、信用额度、总信用额度、循环信贷余额、循环信贷利用率、工作年限等17个作为自变量. 用普通的最小二乘法求解模型(1), 得到的线性回归模型的拟合结果如表1所示, 表1中系数估计值小于0则说明了对借款成功率产生负作用, 越小说明越难借到投资人的款; 若系数估计值大于0则表现为正作用, 值越大说明越容易借到投资人的款. 表中标准差一列, 其值越小说明效果越好[2].

表1 模型(1)最小二乘回归系数估计值
上述对比方法有如下的不足, 当利用条件数判别法进行多重共线性检测时, 这种经典的最小二乘估计方法求解模型(1)的多重共线性条件数k值为134.7464(即判定是否存在多重共线性的条件数k值, 本文把它简称为“共线性数”). 一些研究者认为, 当k>30, 说明共线性问题严重[13,15,16]. 数据有着多重共线性特点, 即线性回归中的解释变量之间由于存在高度相关关系而导致模型参数的置信区间过大、模型估计失真, 使得单个回归系数解释起来很困难, 而且会导致模型的不稳定[17].
对上述Lending Club实验数据, 实验中采用Lasso回归方法(公式(3))构建模型(1), 并用Mallows Cp统计量方法(公式(4))求解模型(1). 实验结果显示, 构建的模型(1)剔除了7个变量, 同时共线性数仅为13.170, 很好的解决了多重共线性问题, 并选出了“最优”的变量子集进行回归, 其Lasso回归模型拟合结果如表2所示. 表2中系数估计值中借款用途、借标人数、资助金额、信用评级等大于0说明对借款成功率产生正作用; 资金需求、利息率、借款时长、房屋所有权、循环信贷余额对借款成功有负作用; 年利率、FICO评分、信用额度、总信用额度、债务与收入比率、循环信贷利用率、工作年限的系数估计为0(即经Lasso回归剔除的变量)对借款成功影响不大. 可知, 我们利用第1.2节中提出的Lasso回归估计方法和系数选择方法, 可有效解决多重共线性的问题, 并能挑选出“最优”的变量子集和得到更好泛化能力的回归模型.
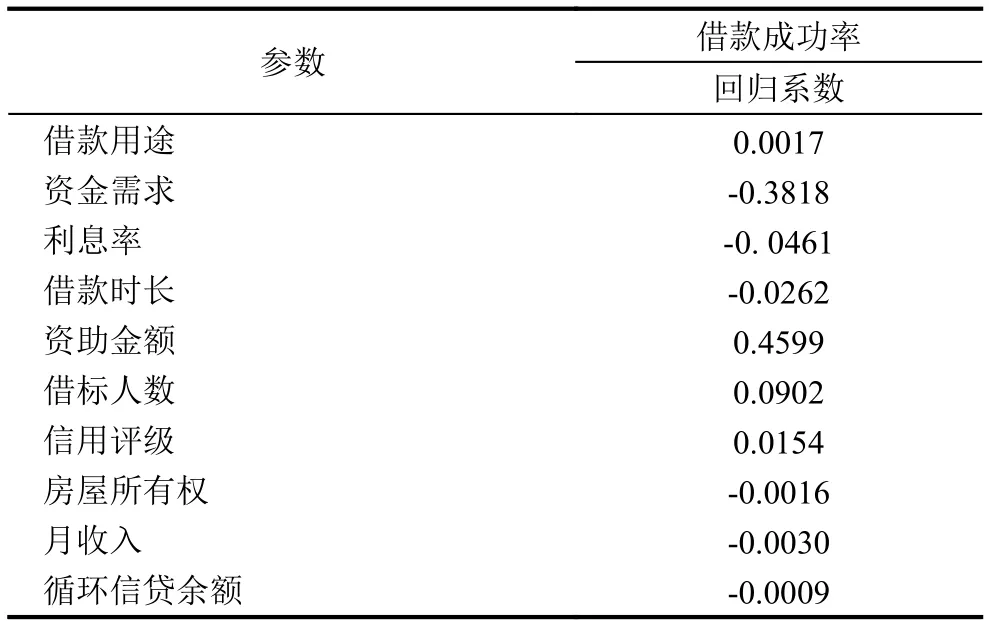
表2 Lasso回归系数估计值
然而, 针对于Lending Club实验数据的借款用途属性共含有七种用途, 不同借款用途对借款成功率的影响程度如何呢?为了验证这七种借款用途对借款成功率的影响, 我们可以在上述采用Lasso回归方法的基础上通过含哑变量的非线性回归模型(5)进一步实验验证. 依据模型(5), 在模型的自变量中增加借款用途这一哑元变量, 用Purposei表示(其值0-其他债务, 1-债务巩固, 2-汽车债务, 3-信用卡, 4-小额商业, 5-家庭改善, 6-大宗购买), 选用资金需求、利息率、资助金额、借标人数、借款时长等借款属性作为模型中的X, 选用信用评级、房屋所有权、月收入、循环信贷余额等借款人属性作为模型中的W, 以借款成功率为因变量P. 可以得出债务巩固、汽车债务、信用卡债务、小额商业、家庭改善、大宗购买、其他债务等七种借款用途的回归系数(见表3). 从表3中可以看出债务巩固(Purpose=1)、信用卡债务(Purpose=3)、小额商业(Purpose=4)、家庭改善(Purpose=5)的回归系数值更大, 显示出比其他借款用途更容易借到款. 回归系数值的结果提示我们, 汽车债务(Purpose=2)、大宗购买(Purpose=6)等借款用途在其他条件不变情况下, 其借款成功率要比其他低较多, 可能是由于这些借款金额比较大, 投资人不放心还款; 投资人往往对用于债务巩固、信用卡债务、小额商业、家庭改善这几种借款用途的借款力度相对支持要大些. 这显示出投资人的出借意愿. 另外,从表3中还可以看出利息率、资金需求、资助金额、借款时长、借标人数、信用评级、房屋所有权、月收入、循环信贷余额等属性对借款成功率的正向和负向影响.
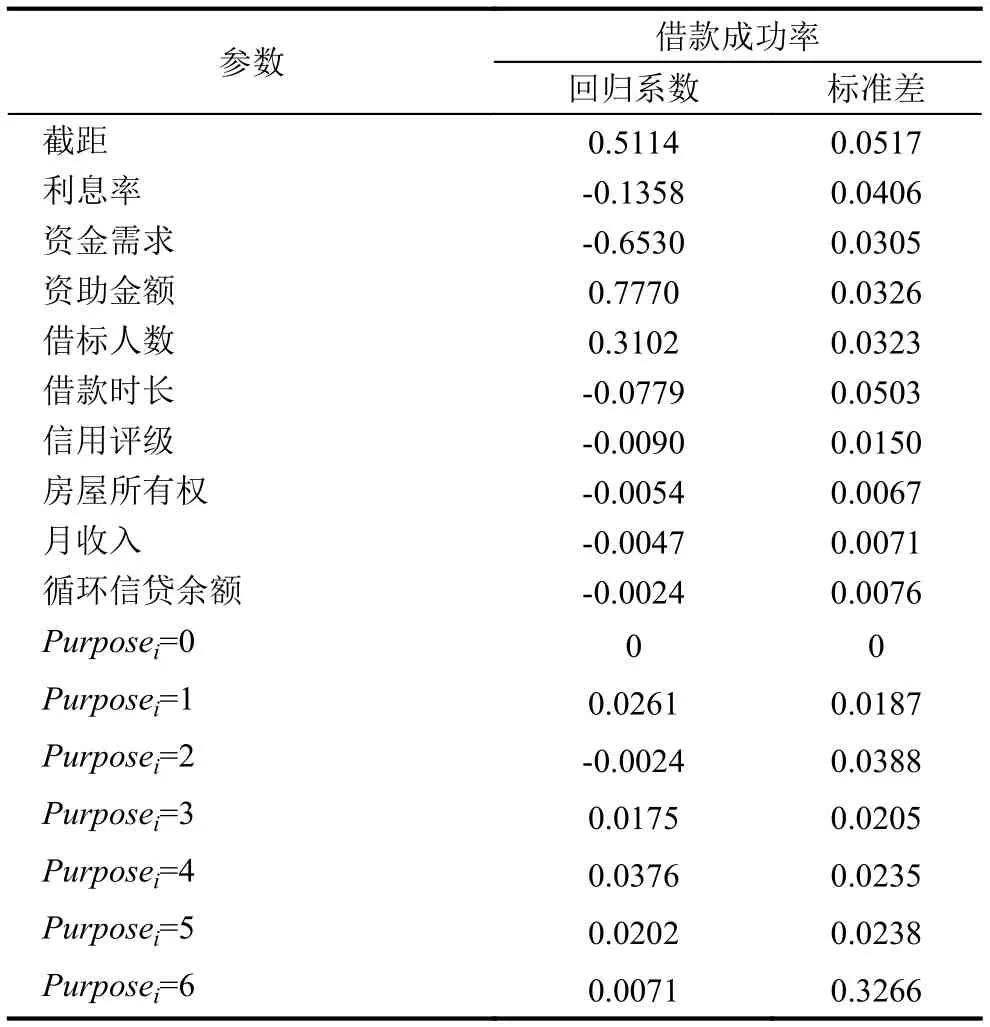
表3 模型(5)的回归系数估计值
在上述实验中, 是通过Lasso回归方法选择变量后,构建全局“最优”的回归模型(5), 把借款用途用哑变量来分析处理, 成功分析出了7种借款用途对借款成功的影响程度. 在对预测借款用途是否影响借款成功率的任务, 评价回归模型的性能时, 我们通常要看它的预测误差、精度怎么样. 从上述实验数据集中选取剩余的三分之一作为测试集用于比较两种模型(即上文的模型(1)、模型(5))的预测误差. 通过对Lending Club平台的数据分析, 表4中给出了这2种回归模型的判定是否具有多重共线性的共线性数、预测误差、模型的拟合优度(或称判定系数). 显然, 模型(5)共线性数仅为13.170, 拟合系数R2达到0.8891, 整体拟合优度都优于模型(1), 而且较好的处理了多重共线性问题, 拟合误差较小, 结果比较合理. 从现在反映的结果来看, 经过Lasso回归筛选变量后所得的变量确实与借款成功率都具有密切的关系, 可以看出Lasso回归在处理多重共线性问题具有很好的效果, 不失为一种处理多重共线性问题的较好方法; 同时, 利用Mallows Cp统计量方法可以选择出全局“最优”的变量子集来进行回归预测.与现有文献中所使用的传统方法(模型1)相比, 本文使用的方法(公式4)及得出的全局“最优”模型(模型5)会使得整个回归方程的拟合精度和拟合效果有相应的提高.

表4 两种模型的拟合结果比较
4 小结
本文对Lending Club平台的数据建立回归模型对影响借款成功率的各种因素进行分析, 用Lasso回归的求解方法有效处理了数据的多重共线性的问题, 剔除与借款成功率相关性不大的因素, 进而得出全局“最优”的变量子集和全局“最优”的回归模型, 从而提高模型的拟合精度和对数据的解释性. 实证研究表明债务巩固、信用卡债务、小额商业、家庭改善等用途的借款成功率明显要高于其他用途.
1Freedman S, Jin GZ. Do social networks solve information problems for peer-to-peer lending? Evidence from Prosper.com. NET Institute Working Paper, 2008: 8–43.
2吴小英, 鞠颖. 基于最小二乘法的网络借贷模型. 厦门大学学报(自然科学版), 2012, 51(6): 980–984.
3陈建中, 宁欣. P2P网络借贷中个人信息对借贷成功率影响的实证研究——以人人贷为例 .财务与金融 ,2013 ,(6) :13–17.
4温小霓, 武小娟. P2P网络借贷成功率影响因素分析——以拍拍贷为例. 金融论坛, 2014, (3): 3–8.
5李渊博, 王珠琳, 朱顺林, 等. P2P网络借贷市场中出借人投标行为影响因子的实证研究——基于信任的视角. 特区经济, 2014, (8): 135–137.
6王会娟, 廖理. 中国P2P网络借贷平台信用认证机制研究——来自“人人贷”的经验证据. 中国工业经济, 2014, (4):136–147.
7李明初. 基于Probit的网络借贷成功影响因素分析——以拍拍贷为例. 会计之友, 2016, (4): 100–106.
8刘严. 多元线性回归的数学模型. 沈阳工程学院学报(自然科学版), 2005, 1(2-3): 128–129.
9Breiman L. Heuristics of instability and stabilization in model selection. The Annals of Statistics, 1996, 24(6):2350–2383. [doi: 10.1214/aos/1032181158]
10曹芳, 朱永忠. 基于多重共线性的Lasso方法. 江南大学学报(自然科学版), 2012, 11(1): 87–90.
11Tibshirani R. Regression shrinkage and selection via the lasso: A retrospective. Journal of the Royal Statistical Society:Series B (Statistical Methodology), 2011, 73(3): 273–282.[doi: 10.1111/rssb.2011.73.issue-3]
12Mallows CL. Some comments on CP. Technometrics, 2000,42(1): 87–94.
13吴喜之. 复杂数据统计方法——基于R的应用. 3版. 北京:中国人民大学出版社, 2015: 36–38.
14Fox J. Component+Residual (partial residual) plots.Technical Report, 1997.
15高惠璇. 处理多元线性回归中自变量共线性的几种方法——SAS/STAT软件(6.12)中REG等过程增强功能的使用. 数理统计与管理, 2000, 20(5): 49–55.
16何晓群, 刘义卿. 应用回归分析. 北京: 中国人民大学出版社, 2001: 154–166.
17Kabacoff RI. R语言实战. 王小宁, 刘撷芯, 黄俊文, 等译.2版. 北京: 人民邮电出版社, 2016: 181–182.
Successful Lending Model Based on LASSO Regression Method
LEE Hai-Chao, WANG Kai-Jun
(Mathematics and Computer Science College, Fujian Normal University, Fuzhou 350007, China)
(Fujian Province Network Security and Cryptography Laboratory, Fujian Normal University, Fuzhou 350007, China)
The trading amount of P2P network lending is rising, and the research of P2P trading data receives much attention. The factor analysis of the success rate of network loan is one of the important research topics. The previous papers on this issue mainly adopt multi-linear regression method, ignoring the problem of multi-collinearity between the variables and the finding of “optimal” regression model. This paper uses the Lasso regression method to establish the regression model with optimal subset of variables, which can analyze the factors that affect the success rate of network borrowing, avoiding the multi-collinearity of the model interference and improving the prediction accuracy of the model.This paper empirically analyzes the borrowing and lending data from the Lending Club platform, and the result shows that our method is significantly superior to the compared approach in the aspects of fitting precision of the model and avoiding the multi-collinearity.
P2P network lending; Lasso regression; multi-collinearity; the success rate borrowings; borrowings purposes
李海超,王开军.基于LASSO回归模型的网贷借款成功影响因素挖掘.计算机系统应用,2017,26(7):204–209. http://www.c-sa.org.cn/1003-3254/5873.html
国家自然科学基金(61672157); 福建师范大学网络与信息安全关键理论和技术创新团队(IRTL1207)
2016-10-24; 收到修改稿时间: 2017-01-04

