Banach空间中一类二阶具阻尼项的积分-微分包含的可控性

刘宏亮,石 峰,朱 琳

(哈尔滨师范大学数学科学学院,黑龙江哈尔滨 150025)

Banach空间中一类二阶具阻尼项的积分-微分包含的可控性

刘宏亮,石 峰,朱 琳

(哈尔滨师范大学数学科学学院,黑龙江哈尔滨 150025)

本文讨论了一类二阶具阻尼项的积分-微分包含问题.利用集值不动点定理将问题转化为求不动点问题,进而得到系统可控性的充分条件.

微分包含;可控性;不动点定理;集值映射

1 引言

Balachandran等[1]讨论了一类二阶积分-微分系统的可控性,利用Schaefer不动点定理,给出了系统可控性的充分条件;Benchohra,Ntouyas[2]利用Martelli压缩集值映射不动点定理,研究了在Banach空间中一类中立型微分和积分微分包含的存在性;Chang-Li[3]利用集值不动点定理,考虑集值函数具有非凸值时二阶微分包含和积分微分包含的可控性.有关具阻尼项的微分包含也进一步发展起来,Benchohra等[4]利用不动点定理研究了集值映射具有凸和非凸值的情形的阻尼微分包含的存在性;Chalishajar[5]利用Ma不动点定理获得了二阶半线性具阻尼项的中立型微分包含可控性的充分条件.到目前为止,有关具阻尼项的微分系统的研究成果参见文献[8,9],但有关具阻尼项的积分-微分包含系统的研究成果尚未见报道.

本文讨论如下具阻尼项的积分-微分包含

可控性的问题,其中E是Banach空间,F：J×E→2E是有界闭凸集值映射.

A是E=(E,‖·‖)中有界线性算子的强连续余弦算子半群{C(t),t∈R}的无穷小生成元.

控制函数u∈L2(J,U),这里U是一个Banach空间,B是从U到E的有界线性算子,D是E上的有界线性算子.

2 预备知识

设(X,‖·‖)是Banach空间,J=[0,m],C(J,E)是从J到X的连续函数构成的Banach空间,赋予范数‖x‖∞=sup{‖x(t)‖：t∈J},L1(J,X)表示 Bochner可积函数x：J→X构成的Banach空间的全体.

记P(X)表示所有非空子集的全体,Pk(X)表示所有紧子集的全体,Pb(X)表示所有有界子集的全体,Pf(X)表示所有闭子集的全体,Pc(X)表示所有凸子集的全体,Pbfc(X)表示所有有界、闭、凸子集的全体.集值映射G：X→P(X),若对于任意的x∈X,G(x)是凸(闭、有界、紧）集,则称G(x)是凸值(闭值、有界值、紧值)映射.对于任意的x0∈X,若对包含G(x0)的任意开集U,存在x0的邻域V使得G(V)⊂U,则称G是上半连续的.若集值函数G是全连续的且具有非空紧值,则G是上半连续的等价于G有闭图,即

若存在x∈X使得x∈G(x),则称G有不动点.设集值函数G：J→Pf(X),若对任意的x∈X,d(w,G(x))=inf{‖w-z‖：z∈G(x)}是J上的可测函数,则称G是可测的.对于任意的x∈X,SG,x表示G(x(·))的所有的 Lebesgue-Bochner可积全体,即

称Banach空间有界线性算子半群{C(t)：t∈R}是强连续余弦算子半群当且仅当

(1)C(0)=I,其中I是在B(X)中的单位算子;

(2)对于任意的s,t∈R,C(t+s)+C(t-s)=2C(t)C(s);

(3)对于任意x∈X,映射t→C(t)x是强连续.结合给定的强连续余弦算半群{C(t)：t∈R},定义

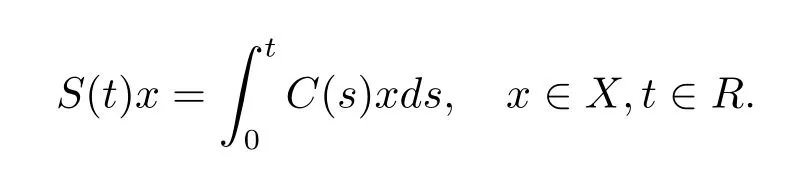
则称{S(t)：t∈R}是强连续正弦算半群.令A：X→X,定义为

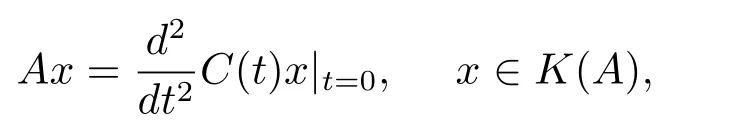
其中K(A)={x∈X：C(t)x是关于t的二次连续可微函数},则称A为强连续余弦族{C(t)：t∈R}的无穷小生成元.定义E={x∈X：C(t)x是关于t的一次连续可微函数}.

引理2.1[6]设X是一个Banach空间,设集值函数G：J×X→Pbfc(X)满足

(1)对于任意的x∈X,(t,x)→G(t,x)是关于t可测的;

(2)对于几乎处处的t∈J,(t,x)→G(t,x)关于x是上半连续的;

(3)对每个固定的x∈C(J,E),集合

非空的.并且设Γ：L1(J,X)→C(J,X)是线性连续映射,则

是C(J,X)×C(J,X)上的闭图算子.

引理2.2[7](Leray-Schauder替换定理)设X是Banach空间,C⊆X是X的非空凸子集,0∈C,集值映射G：C→Pk,c(C)是上半连续的,并且映C的有界子集为相对紧集,则下述论断必有一个成立

(1)集合Γ={x∈C：x∈λG,λ∈(0,1)}是无界的;

(2)集值映射G(·)在C中存在不动点.

定义2.1函数y(·)∈C(J,E)满足

并且y(0)+f(y)=y0,y′(0)=z0,则y(·)称为系统 (1.1)-(1.2)的 mild解.

定义2.2系统(1.1)-(1.2)在J上可控,是指对任意的y0∈K(A)和z0∈E1,存在控制u∈L2(J,U),使得系统(1.1)-(1.2)的mild解满足y(m)+f(y)=y0.

我们需要如下假设

(A1)A是Banach空间E上有界线性算子的强连续余弦算子半群{C(t)：t∈J}的无穷小生成元,且存在常数M＞0,使得M=sup{‖C(t)‖：t∈J}.

(A2)f是全连续的,且存在常数L＞0,使得对任意的y∈E,||f(y)||≤L.

(A3)线性算子W：L2(J,U)→E,定义为),存在取值于L2(J,U)kerW上的有界逆算子W-1,且存在M1,M2＞0,使得‖B‖≤M1,‖W-1‖≤M2.

(A4)F：J×E→Pbfc(E),且F满足对任意的y∈E,t→F(t,y)是可测的,对于几乎处处t∈J,y→F(t,y)是上半连续的;对每个固定的y∈C(J,E),集合

为非空的;

(A5)存在一个连续非降函数ψ：R+→(0,∞),及p(t)∈L1(J,R+)对于几乎处处的t∈J,y∈E有

(A6)对于任意的t∈J,β(t,s)在[0,t]上可测,并且

在J上有界;

(A7)从J到L∞(J,R),映射t→βt是连续的,其中βt(s)=β(t,s).

3 主要结果

定理3.1若假设条件(A1)-(A7)成立,并且存在正数θ＞0,使得

其中

则系统(1.1)-(1.2)是可控的.

证由(A3),对任意的y(·)∈C(J,E),定义控制函数

其中

利用控制函数定义集值映射Φ(·)：C(J,E)→2C(J,E),具有如下形式

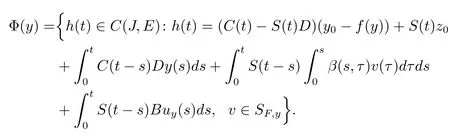
(1)对于任意的y∈C(J,E),y是凸的.

设h1,h2∈Φy,存在v1,v2∈SF,y,使得对任意的t∈J,有

令0≤α≤1,有

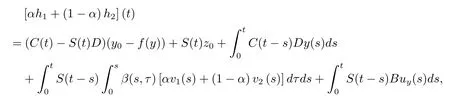
因为F有凸值,SF,y是凸的,则αh1+(1-α)h2∈Φy.

(2)Φ把C(J,E)中的有界集映成有界集.

令Vq={y∈C(J,E),‖y‖≤q},要证存在一个正数˜l,使得对任意的y∈Vq,h∈y,有‖h‖∞≤ ˜l.若h∈Φy,则存在v∈SF,y,使得

对任意的t∈J,由假设(A1)-(A7)知

其中

(3)Φ将C(J,E)中的有界集映射为等度连续的集合.设t1,t2∈J,0＜t1＜t2,对任意的y∈Vq,h∈Φy,使得(3.2)式成立,于是有

当t2→t1时,上述不等式右端趋于零,因而Φ(Vq)是等度连续的.

(4)Φ把有界集映射为E中的相对紧集.固定0＜t≤m,并且实数ε满足0＜ε＜t,对于任意的y∈Vq,定义

因为C(t)和S(t)是紧算子,集合Yε(t)={hε(t)：hε(t)∈Φy}是相对紧集.对于每一个h∈y,当ε→0+时,‖h(t)-hε(t)‖→0,因此存在相对紧集任意逼近集合{h(t)：h∈Φy}.从而,{h(t)：h∈Φy}是相对紧的.因此算子Φ是全连续的集值映射.

(5)Φ(·)有闭图象.令yn→y∗,hn∈Φyn,且hn→h∗,要证h∗∈Φy∗.事实上,hn∈yn,则存在vn∈SF,yn,使得

需要证明存在v∗∈SF,y∗使得

令

由f,W-1和D是连续的,则,∀t∈J.从而当n→∞时,

定义线性连续算子 Γ：L1(J,E)→C(J,E),

并且

由引理2.1知Γ◦SF,y是闭图算子,并且有

因为yn→y∗,所以

因此Φ是具有闭凸值且上半连续的集值映射.

由引理2.2知,为了证明Φ有不动点,还需要下面一个步骤.

令对于任意的λ∈(0,1),y∈λΦ(y)的t∈J,存在v∈SF,y使得

对任意的t∈J,有

因此

由(3.1)式知存在Φ,使得‖y‖/θ.设集合U={y∈C(J,E),‖y‖＜ θ}.在U中,当λ∈(0,1)时,不存在y∈∂U满足y∈λΦ(y).因此由引理2.2知Φ有不动点,则系统(1.1)-(1.2)是可控的.

[1]Balachandran K,Park D.G,Manimegalai P.Controllability of second-order integrodifferential evolution systems in Banach spaces[J].Comp.Math.Appl.,2005,49：1623-1642.

[2]Benchohra M,Ntouyas S K.Existence results of neutral functional di ff erential and integrodi ff erentail inclusions in Banach spaces[J].Elec.J.Di ff.Equ.,2000,20：1-15.

[3]Chang Y K,Li W T.Controllability of second-order di ff erential and inegrodi ff erential inclusions in Banach spaces[J].J.Optim.The.Appl.,2006,129(1)：77-87.

[4]Benchohra M,Gatsori E P,Ntouyas,S K.Nonlocal quasilinear damped di ff erential inclusions[J].Elec.J.Di ff.Equ.,2002,7：1-14.

[5]Chalishajar D N.Controllability of damped second order semi-linear neutral functional di ff erential inclusions in Banach spaces[J].Auto.Contr.Syst.J.,2009,2：1-7.

[6]Lasota A,Opial Z.An application of the Kakutani-Ky-Fan theorem in the theory of ordinary di ff erential equations[J].Bull.Acad.Polon.Sci.,1965,13：781-786.

[7]Dugundij J,Grans A.Fixed point theory[M].Warsaw：Mongra fi e Mat.PWN,1982.

[8]Lin Q,Yu Y.Interval oscillation criteria for emden-fowler equation with a damping term[J].J.Math.,2012,32(4)：716-722.

[9]Jiang L,Ding W.Periodic solutions of damped impulse systems[J].J.Math.,2016,36(5)：920-928.

CONTROLLABILITY OF SECOND-ORDER DIFFERENTIAL INCLUSIONS IN BANACH SPACE WITH DAMPED AND INTEGRAL TERMS

LIU Hong-liang,SHI Feng,ZHU Lin
(College of Mathematics Science,Harbin Normal University,Harbin 150025,China)

In this paper,a class of di ff erential inclusions with the damped term and integral term in Banach space was studied.By using fi xed point theorem,a sufficient condition for the controllability for such di ff erential inclusion was obtained.

di ff erentail inclusion;controllability; fi xed point theorem;multivalued map

on：34A60

O175.12

A

0255-7797(2017)04-0811-08

2016-03-31接收日期：2016-12-01

黑龙江省教育厅教育项目(12541242).

刘宏亮(1978-),男,河北秦皇岛,副教授,主要研究方向：运筹与控制.

石峰.