基于改进LHS方法的翼型水下滑翔机水动力外形优化

王振宇，王亚兴，俞建成，张艾群

（1．中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；2．中国科学院大学，北京 100049）

基于改进LHS方法的翼型水下滑翔机水动力外形优化

王振宇1,2，王亚兴1，俞建成1，张艾群1

（1．中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；2．中国科学院大学，北京 100049）

针对如何获得翼型水下滑翔机最佳升阻比外形这个问题，提出了基于改进拉丁超立方抽样方法的翼型水下滑翔机外形优化方法。分别应用中值拉丁超立方抽样方法和改进拉丁超立方抽样方法从翼型水下滑翔机参数化模型中进行二次取样，利用计算流体力学（CFD）方法计算其在水中做匀速运动时的升力系数和阻力系数，获得翼型水下滑翔机优化模型。对比改进拉丁超立方抽样方法和中值拉丁超立方抽样方法的优化结果表明：在相同样本数量条件下，改进拉丁超立方抽样方法可以获得更好的优化结果。

翼型水下滑翔机；拉丁超立方抽样；模型试验；流体力学

自1989年Henry Stommel提出“水下滑翔机”的概念以来[1-4],各种类型的水下滑翔机纷纷问世。1995年开始，美国在海军研究局（ONR）资助下，先后研制出SLOCUM，Seaglider和Spray等多种可以长时间独立作业的水下滑翔机[5-7]。翼型水下滑翔机作为一种新概念水下滑翔机，在保留传统水下滑翔机低功耗、长航程的基础上，采用翼身一体化布局。翼身融合（Blended Wing Body，BWB）布局最早被提出应用于一种机身与机翼融合在一起的飞机布局上，这种飞机布局具有升阻比高、结构质量轻、油耗低、隐身性能好等特点[8-9]。美国 ONR[10-11]经过对翼型水下滑翔机样机X-RAY和Z-RAY的研究，证明翼身一体化布局可以有效提高水下滑翔机的水动力效率。Graver等[12]对比多种水下滑翔机水动力外形，认为采用翼身一体化布局的翼型水下滑翔机适用于大攻角、小姿态角的滑翔状态。

近年来，国内外学者针对水下滑翔机的水动力性能进行了一系列研究。胡克等[13]对首尾为半球形的机体和经椭圆修正机体受到的阻力进行计算，发现首尾线型经过椭圆修正的机体的阻力明显降低。李志国等[14]在对不同前缘的后掠梯形翼进行的试验研究中发现阻力系数不随后掠角的变化而单调变化。M.Arima等[15]对主翼角度可调的水下滑翔机进行了研究。与固定翼式水下滑翔机相比，此类滑翔机可在阻力小得多的滑翔角下巡航。陈亚君等[16]从降低能源消耗方面对水下滑翔机的水动力性能进行优化。李永成等[17]从阻力、功转换率及重心偏移量等多方面对水下滑翔机的性能进行评估，得出水下滑翔机整机主体外形和机翼后掠角对水动力性能的影响。

为了均衡精度与效率之间的矛盾，国内外学者对数值模型的优化方法开展了大量工作。徐昌文等[18]将形状优化、模糊优化和遗传优化相交叉，促进了船舶结构优化设计的深入发展；闫晋辉等[19]将纵骨穿越强横梁和扶强材作为研究对象，以初步定义尺寸为基准，利用ABAQUS软件建立多种模型并进行计算分析，从而得出优化的节点形式；刘洋等[20]将并行遗传算法作为优化方法，应用于耐压壳结构的优化设计。丁浩等[21]应用全因子实验模拟,拟合了静水中扑翼推力与运动参数之间的函数关系。SIMPSON W等[22]通过实验验证论述了不同实验设计方法的特点，并为各种方法在工程实践中的应用提出指导性建议。JEON等[23-24]将代理模型应用于飞机机翼的翼型优化。谷海涛等[25]基于代理模型对水下滑翔机的机翼设计进行优化。

随着计算流体力学技术的发展，对水下滑翔机外形的数值模型优化方法逐步取代了花费高、周期长的实验模型优化方法。拉丁超立方抽样方法作为一种多维分层抽样方法，被广泛应用于实验设计中。邓乾旺等[26]将拉丁超立方抽样方法应用于薄板装配误差分析中；祁恩荣等[27]将拉丁超立方抽样方法应用于船体极限强度的可靠性分析。对于翼型水下滑翔机整体外形的优化，本文应用中值拉丁超立方抽样方法对样本空间进行优化，对优化后的样本空间应用改进拉丁超立方抽样方法进行二次抽样，这样可以缩小样本空间，在抽样数量保持不变的情况下，有效提高了优化采样精度。利用计算流体力学（CFD）方法计算其在水中做稳态运动时的升力系数和阻力系数，获得翼型水下滑翔机优化模型。

1 优化设计方法

优化过程首先采用中值拉丁超立方抽样法（MidtermLatin hypercube sampling，MLHS）[28]对变化范围内的设计变量进行一次抽样。综合考虑取样密度和模型水动力参数计算时间确定抽取样本的数量。对抽取样本进行水动力参数仿真计算，根据一次抽样仿真结果的分布对抽取的样本进行分析筛选。对筛选后的样本空间应用改进拉丁超立方抽样方法进行二次抽样，对抽取的样本进行水动力参数计算，得出优化后的翼型水下滑翔机外形。

1.1 一次抽样

应用中值拉丁超立方抽样方法对设计变量的样本空间进行一次抽样，抽样过程中假定各变量之间相互独立。拉丁超立方抽样方法是一种多维分层实验设计方法[29-30]。假设抽样空间维数为n，xi∈[li, ui],i=1,2,…,n；xi为第i维变量，li,ui分别为第i维变量的下界和上界，拉丁超立方在抽样空间中产生n0个样本点的具体做法如下：

（1）确定抽样规模n0；

（2）将每一维变量xi的定义区间[li,ui]等分为n0个相等区间：

li=xi0＜xi1＜…＜xij＜xi(j+1)＜…＜xin0=ui，这样就将原来n维的抽样空间划分为nn0个小超立方体；

（3）产生一个n0×n的矩阵U，U的每一列均为{1,2,3,…,n0}的一个随机全排列，U称为拉丁超立方阵；

（4）U的每一行都对应一个被选中的小超立方体，在每一个被选中的小超立方体中随机产生一个样本点，这样就得到n0个样本点。中值拉丁超立方抽样方法（MLHS）是抽取每个小超立方体内的中间点作为样本点。

1.2 二次抽样

二次抽样过程应用改进拉丁超立方抽样方法，通过对输入随机变量分层后最靠近其期望值的超立方体边界作为取样点。选择原则是：在期望均值左半平面选取超立方体的右边界，右半平面选取超立方体的左边界。MLHS方法的关键在于区间内取点，仅体现了“分层”的思想，而改进LHS方法的关键在于选取趋近期望值的边界顶点，综合了“分层”和“重要性”的思想，从而使改进LHS的收敛性具有独特的特征[31]。

一次抽样过程中假定各设计变量相互独立。实际各设计变量之间存在相关性，二次抽样过程中依据一次抽样计算结果建立变量协方差矩阵，作为二次抽样的变量相关性输入。

n维随机变量(X1,X2,…,Xn)的两个随机变量Xi和Xj之间的协方差定义为：

式中：E[Xi]和E[Xj]分别代表随机变量Xi和Xj的期望。

协方差表示两个变量总体误差的期望。如果两个变量的变化趋势一致，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，那么两个变量之间的协方差就是负值。如果Xi和Xj是相互独立的，那么二者之间的协方差就是0。随机变量(X1,X2,…,Xn)的协方差矩阵定义为：

1.3 参数化模型水动力参数仿真计算

计算采用SIMPLEC算法结合层流模型和RNGk-ε湍流模型组成的混合模型计算雷诺平均纳维-斯托克斯方程（RANS）。对流场采用有限体积法求解RANS方程，湍流模型选择k-ε模型[32]，选择标准壁面函数。为使计算更加准确，收敛更快，使用结构化网格对流场进行划分，为避免流域边界对流场产生影响，流场应足够大，整个外域采用长方体。流场的总长度取载体弦长的10倍，流场宽度取载体翼展的6倍[33]。建立翼型水下滑翔机的参数化模型，将模型自动导入CFD程序迭代计算。为了对不同模型的计算结果进行比较，对CFD的计算结果进行无量纲化处理。与常规滑翔机的回转体外形不同，翼型水下滑翔机采用翼身融合技术，参照飞行器选取机翼面积为参考面积[34]，无量纲化表达式为：

式中：CL为升力系数；CD为阻力系数；L为升力；D为阻力；ρ为液体密度；S为参考面积；U为来流速度，升力L和阻力D是关于攻角α和来流速度U的函数。

2 翼型水下滑翔机模型参数化

美国海军研究所研制的Z-Ray水下滑翔机采用了翼身一体化布局，试验证明Z-Ray具有较好的水动力效率[11]。本文将Z-Ray的外形作为基准外形（如图1所示），在此基础上进行优化。为了便于与基准外形进行对比，翼型水下滑翔机参数化模型的翼展和弦长与基准外形一致，其中翼展l=5 m,中心弦长b1=2 m，翼稍弦长b2=0.12 m，选定前缘半径、后缘半径、翼稍距、翼前缘角、翼后缘角为设计变量。为了保证不会出现奇异外形，外形参数设计变量及其基准和取值范围如表1所示。

图1 翼型水下滑翔机基准外形

表1 设计变量的基准值与变化范围

3 优化结果

对翼型水下滑翔机的优化过程分两步，首先通过MLHS方法一次抽样来缩小样本空间，然后通过改进LHS方法对优化后的样本空间进行二次抽样，取得翼型水下滑翔机优化模型。在保证取样数量相同的前提下，将采用LHS方法的优化结果与采用MLHS方法的优化结果进行对比，对比结果证明采用改进LHS方法的优化结果具有明显的提升。

3.1 MLHS方法模型初步优化

通过MLHS抽样法随机抽取50组模型参数，通过参数化模型水动力参数仿真计算对这50组模型进行性能评估，仿真模型的网格数为150～200万。为了便于各组模型间的相互性能评估，计算中来流速度取0.514 4 m/s，攻角取3°。

图2所示为对50组抽样模型水动力性能计算结果进行无量纲化处理后升力系数CL和阻力系数CD的分布图，图3所示为初步优化升阻比分布图。

图2 模型升力系数CL和阻力系数CD的分布图

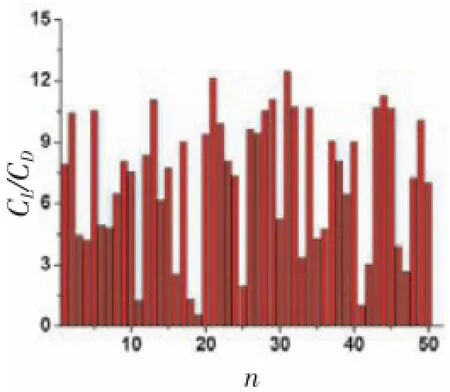
图3 MLHS方法初步优化升阻比分布图

表2所示为优化前后CL/CD的对比，对一次抽样的仿真结果进行分析，选出升阻比大于10的参数模型用于改进LHS方法的二次抽样。表3所示为通过MLHS方法对翼型水下滑翔机外形优化后选取的模型参数。

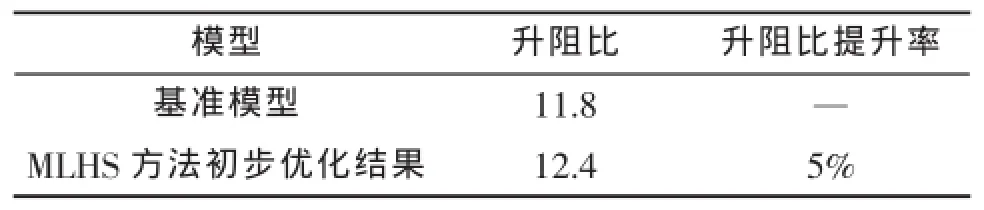
表2 优化前后CL/CD对比

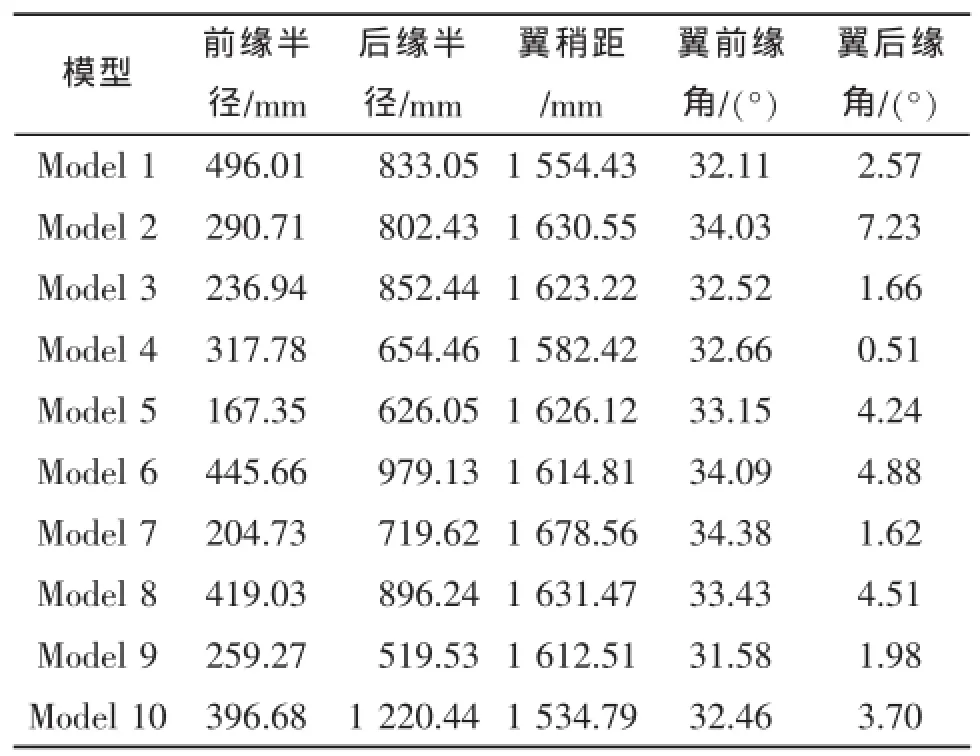
表3 初步优化选取模型参数

3.2 改进LHS方法模型优化

将MLHS初步优化的结果作为改进LHS方法优化的输入量。通过建立各设计变量之间协方差矩阵引入“相关因子”，将初步优化最优模型的变量参数作为改进LHS方法的期望值，通过改进LHS方法对翼型水下滑翔机外形进行优化。

将筛选后的模型参数（表3所示）代入式（2）得出各设计变量之间的协方差矩阵Σ（式（5）所示）。将MLHS方法初步优化结果的变量参数作为期望值，将式（5）作为改进LHS方法的输入量，抽取50组样本，对抽取样本进行CFD计算。

对样本仿真结果进行无量纲化处理后升力系数CL和阻力系数CD的分布如图4所示，图5所示为二次优化升阻比分布图，与图2、图3对比可以看出改进LHS的优化结果比MLHS初步优化结果更加趋近于最优模型。表4为优化前后CL/CD对比。对比结果可以看出通过优化翼型水下滑翔机升阻比性能提升11%。图6所示为翼型水下滑翔机优化模型与基准模型的对比图。

图4 二次优化模型升力系数CL和阻力系数CD的分布图

图5 二次优化升阻比分布图

表4 优化前后CL/CD对比

图6 翼型水下滑翔机优化后升阻比最优模型与基准模型对比

3.3 改进LHS抽样方法与MLHS抽样方法结果对比

应用MLHS抽样方法从样本空间抽取100组样本，对样本进行CFD计算，图7所示为MLHS方法优化后CL和CD分布图，图8所示为MLHS方法优化后升阻比分布图。由表5基准模型、MLHS方法和改进LHS方法优化模型的升阻比对比可以看出改进LHS方法的优化效果好于MLHS方法。

图7 MLHS方法优化后CL和CD分布图

图8 MLHS方法优化升阻比分布图

表5 基准模型、MLHS方法和改进LHS方法优化模型CL/CD对比

4 结论

本文将升阻比作为评价翼型水下滑翔机水动力性能优劣的评价指标，通过MLHS抽样方法和改进LHS抽样方法对翼型水下滑翔机参数化模型进行二次优化，优化后翼型水下滑翔机的升阻比相比基准模型提升了11%。同时，将优化结果与采用MLHS抽样方法的优化结果进行对比，优化结果表明在相同抽样样本情况下，采用改进LHS方法的优化结果有明显的提升。

[1]BachmayerR,LeonardNE,GraverJ,etal.Underwatergliders:Recentdevelopmentsandfutureapplications[C]//ProcIEEEInternational Symposiumon Underwater Technology UT’04,2004:195-200.

[2]Willcox J S,Bellingham J G,Zhang Y,et al.Performance metrics for oceanographic surveys with autonomous underwater vehicles[C]// IEEE J Oceanic Eng,2001:711-725.

[3]张少伟,俞建成,张艾群.水下滑翔机垂直面运动优化控制[J].控制理论与应用,2012,29(1).

[4]Stommel H.The SlocumMission[J].Oceanography,1989,32(4):93-96.

[5]Rudnick DL,Davis R E,Eriksen CC,et al.Underwater gliders[J].Ocean research marine technologySocietyJournal,2004,38(1):48-59.

[6]Webb D C,Simonetti P J,Jones C P.SLOCUM:an underwater glider propelled by environmental energy[J].Oceanic Engineering IEEE Journal of,2001,26(4):447-452.

[7]Sherman J,Davis R E,Owens W B,et al.The autonomous underwater glider"Spray"[J].Oceanic Engineering IEEE Journal of,2001, 26(4):437-446.

[8]Liebeck R H.Design ofthe Blended WingBodySubsonic Transport[J].Journal ofAircraft,2004,41(1):10-25.

[9]李晓勇,张淼,鲁素芬,等.翼身融合飞机的空气动力学研究进展[J].飞机设计,2007,27(2):1-9.

[10]ONR.Liberdade XRAY advanced underwater glider.https://www.onr.navy.mil/media/extra/fact_sheets/advanced_underwater_glider. pdf.U.S.Office ofNaval Research,2006.

[11]ONR.ZRay.The New Generation Flying Wing UnderwateGlider:Status and Promise.http://www.onr.navy.mil/en/Media -Center/Fact-Sheets.2010.

[12]Graver J G.Underwater gliders:Dynamics,control and design[D].Princeton University,2005.

[13]胡克,俞建成,张奇峰.水下滑翔机器人载体外形设计与优化[J].机器人,2005,27(2):108-112.

[14]李志国,朱鹏程,李锋.小展弦比机翼低雷诺数升阻特性试验研究[J].流体力学实验与测量,2004,18(4):78-82.

[15]Arima M,Miwa Y,Ikebuchi T.Performance assessment of an underwater glider with independently controllable main wings by CFD analysis[C]//Sixth International Symposiumon Underwater Technology.Wuxi,China,2009.

[16]Chen Y,Chen H,ZhengMA.Hydrodynamic analyses oftypical underwater gliders[J].Journal ofHydrodynamics,Ser.B,2015,27(4): 556-561.

[17]陈亚君,李永成,马峥,等.水下滑翔机水动力外形的选型分析[J].中国造船,2015,56(3):39-48.

[18]徐昌文．船舶结构优化设计的研究进展[J]．上海交通大学学报，1998，32(11)：118-120，134．

[19]闫晋辉，蔡斯渊，王德．船舶结构典型节点的优化分析[J]．舰船科学技术，2011，33(11)：5l-55，88．

[20]刘洋.基于遗传算法的水下无人潜器结构特性优化分析[J].舰船科学技术，2015,37(9):145-149．

[21]丁浩.仿生扑翼水下航行器推进特性及运动性能研究[D].西安：西北工业大学，2015.

[22]Simpson T W,LIN D K J,Chen W.Sampling strategies for computer experiments design and analysis[J].International Journal of Reliabilityand Applications,2001,2(3)：209-240.

[23]Jeon K S,LEE J W,Byun Y H.Development of repretitive response surface enhancement Technique forthe multidisciplinary systemoptimization[C]//47thAIAA/ASME/ASCE/AHS/ASC Structures,StructuralDynamics,and Materials Conference,May 1-4, 2006,Newport,Rhode Island.Rhode Island：AIAA,2006：1-9.

[24]Jouhaud J C,Sagaut P,Montagnac M,et al.Asurrogate-model based multidisciplinary shape optimization method with application to a 2Dsubsonic airfoil[J].Computers&Fluids,2007(36)：520-529.

[25]谷海涛,林扬,胡志强,等.基于代理模型的水下滑翔机机翼设计优化方法[J].机械工程学报，2009，45(12):7-14.

[26]邓乾旺,文文.基于拉丁超立方抽样的薄板装配误差分析[J].中国机械工程,2012,23(8):947-951.

[27]祁恩荣,崔维成.船体总纵极限强度可靠性分析的拉丁超立方抽样法[J].船舶力学,2002(3):52-61.

[28]McKay M D,Beckman R J,Conover W J.A comparison of three methods for selecting values of input variables in the analysis of output froma computer code[J].Technometrics,2000,42(1):55-61.

[29]MaC,FangKT.Anewapproach toconstruction ofnearlyuniformdesigns[J].InternationalJournalofMaterials and Product Technology, 2004,20(1-3):115-126.

[30]方开泰.均匀试验设计的理论,方法和应用-历史回顾[J].数理统计与管理,2004,23(3):69-80.

[31]李俊芳,张步涵.基于进化算法改进拉丁超立方抽样的概率潮流计算[J].中国电机工程学报,2011,31(25):90-96.

[32]王福军.计算流体动力学分析［M］.北京:清华大学出版社，2004：202-204.

[33]胡志强.海洋机器人水动力数值计算方法及其应用研究[D].北京：中国科学院大学,2013.

[34]李为吉,王正平,艾剑良,等.飞机总体设计[M].西安：西北工业大学出版社,2005.

Hydrodynamic Shape Optimization for the Flying-Wing Underwater Glider Based on Improved LHS Method

WANG Zhen-yu1,2,WANG Ya-xing1,YU Jian-cheng1,ZHANG Ai-qun1
1.State Key Laboratory of Robotics,Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,Liaoning Province,China; 2.University of Chinese Academy of Sciences,Beijing 100049,China

A shape optimization method is proposed for underwater gliders based on improved LHS sampling method,in order to obtain the optimal hydrodynamic shape of the flying-wing underwater glider with optimized lift-to-drag ratio.The median sampling method and improved Latin hypercube sampling method are used to carry out the two sampling tasks in the parametric model of the flying-wing underwater glider.The computational fluid dynamics (CFD)method is adopted to calculate the lift coefficient and drag coefficient of the underwater glider. The optimization results show that the improved Latin hypercube sampling method can achieve better optimization results under the condition of the same number of samples.

flying-wing underwater glider;Latin hypercube sampling;model tests;lift-to-drag ratio;fluid mechanics

P716

A

1003-2029（2017）03-0050-07

10.3969/j.issn.1003-2029.2017.03.010

2017-05-16

王振宇（1986-），男，博士研究生，主要从事水下机器人载体设计、水下机器人水动力分析等方面的研究。E-mail:wangzhenyu@sia.cn