基于LWPT-DTW的间歇过程不等长时段数据同步化

王建林，刘伟旻，邱科鹏，张维佳，于涛

（北京化工大学信息科学与技术学院，北京 100029）

基于LWPT-DTW的间歇过程不等长时段数据同步化

王建林，刘伟旻，邱科鹏，张维佳，于涛

（北京化工大学信息科学与技术学院，北京 100029）

间歇过程不等长时段数据直接影响数据驱动的多元统计分析时段建模精度，导致间歇过程的监控性能降低。针对间歇过程不等长时段数据问题，提出一种基于提升小波包变换（LWPT）和动态时间规整（DTW）算法的间歇过程不等长时段数据同步化方法。该方法引入LWPT对间歇过程不等长时段数据轨迹进行高低频的多级分解，充分提取数据轨迹的所有时频域信息；采用DTW算法对不同频段的系数矩阵进行同步化，并利用提升小波包逆变换对同步化后的系数矩阵进行合成，降低吉布斯现象对数据轨迹合成的影响，获得等长的时段轨迹，实现了间歇过程不等长时段数据同步化。青霉素发酵过程仿真实验表明，所提出的方法运算速度快、稳定，不等长时段数据的同步化结果具有较高的准确性，为间歇过程时段建模提供了可靠的过程数据。

不等长时段数据；同步化；提升小波包变换；动态时间规整；间歇过程

引 言

间歇过程是现代工业中重要的生产方式，在精细化工、制药及食品等领域有着广泛的应用[1-2]。基于数据驱动的间歇过程多元统计建模及监测，促进了其生产安全、运行可靠和产品质量的提高。间歇过程具有复杂的过程特性，多时段是间歇过程的固有特征[3-4]，若将单批次的多时段间歇过程当作一个整体进行过程建模和监测，将导致所建过程模型难以准确描述间歇过程，并造成较高的间歇过程监测误报率和漏报率；同时间歇过程的不同批次对应时段的操作时间因生产原料的质量差异、初始条件的设置差异等出现不同步，导致各个批次对应时段的数据长度不一致，难以满足数据驱动的多元统计分析过程建模和监测方法[5-6]对过程数据长度一致性的要求，因此解决间歇过程不等长时段数据问题，能够为基于多元统计分析的间歇过程时段建模和监测提供可靠的过程数据。

传统的间歇过程不等长数据轨迹同步化方法有：最短长度法[7]和最长长度法[8]，即分别以最短长度批次和最长长度批次作为参考批次，将其他批次通过截取或者填充的方法实现同步化，这两种方法计算简单，但容易丢失过程数据中的重要信息或引入累赘信息。动态时间规整（dynamic time warping，DTW）算法[9-10]，基于动态规划原理，灵活匹配不同模式之间的相似特征，已在间歇过程的不等长时段数据同步化中得到应用[11-13]。近年来出现了改进的 DTW 算法，Bork等[14]利用 derivative DTW（DDTW）算法解决了间歇过程不等长时段数据同步化中的峰值漂移问题；Zhang等[15-16]在DDTW算法的基础上构建了一种robust DDTW（RDDTW）算法，用于间歇过程不等长时段数据同步化，降低了测量噪声带来的误差，然而没有充分提取时段数据轨迹的所有时频域信息。这些算法均是在时域对间歇过程不等长时段数据同步化，仅仅是挖掘不等长时段数据的时域信息，而且计算量大、运算速度慢。Li等[17]将离散小波变换和DTW算法相结合，给出一种多尺度DTW（multi-scale DTW，MSDTW）算法，用于间歇过程的不等长时段数据同步化，取得了较好的同步化结果；Barbon等[18]应用MSDTW算法同步化不等长数据轨迹，提高了同步化过程的运算速度。然而MSDTW方法中的离散小波变换仅仅对轨迹的低频部分进行多级分解，忽略了高频部分的分解[19-20]，没有挖掘高频部分的有用信息，且处理具有突变点的轨迹时会出现吉布斯现象[21]，增加了轨迹的合成误差，因此MSDTW方法具有一定的局限性，制约了该方法的实际应用。

本文引入提升小波包变换（lifting wavelet package transform，LWPT）解决间歇过程不等长时段数据问题，提出一种基于 LWPT-DTW 的间歇过程不等长时段数据同步化方法，利用提升小波包变换对不等长时段数据轨迹进行高低频多级分解，充分提取数据轨迹的所有时频域信息，使用DTW算法对分解后得到的不同频段的系数矩阵进行同步化，并利用提升小波包逆变换进行合成，降低吉布斯现象对数据轨迹合成的影响，实现了不等长时段数据同步化，运算速度快，获得的同步化结果具有更高的准确性，最后通过青霉素发酵过程仿真验证所提方法的有效性。

1 基于MSDTW的不等长时段数据同步化

1.1 基于DTW的不等长时段数据同步化

设T和R代表间歇过程中的时段数据待同步化轨迹和参考轨迹，分别为t×N维和r×N的数据矩阵，t和r为两轨迹的时间长度，N是被测变量的个数。T和R的局部距离为

其中，1≤i≤t，1≤j≤r。局部距离 d是指 T和 R点对点的距离，刻画两轨迹之间的局部特征。设D为正向累积距离矩阵，根据局部约束[22]用动态规划算法可以由d(i, j)得到D(i, j)，递推式为

初始条件为D(1,1)2d(1,1)，T和R的最短距离为。基于最短距离*D进行反向寻优获得一条处于t×r网格中的最优路径，如图1所示。通过最优路径对T和R进行点对点的匹配，当出现T中的多个点同时与R中的一个点匹配时，如图1所示，T的A和B两点同时与R的点C匹配，设点C对应的时刻为k，采取多点平均法[23]完成匹配，T第k时刻的值为

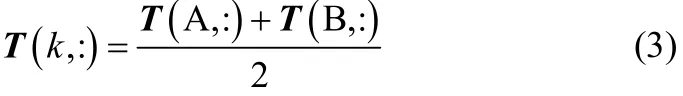
经过同步化后，T和R具有一致的时间长度。

图1 DTW同步化路径Fig.1 Synchronization path of DTW

图2 MSDTW方法(a)和同步化路径(b)，LWPT-DTW方法(c)和同步化路径(d)Fig.2 MSDTW method(a) and synchronization path (b)，LWPT-DTW method(c) and synchronization path (d)

1.2 基于MSDTW的不等长时段数据同步化

MSDTW[18]是基于离散小波变换[19]和 DTW 算法提出的间歇过程不等长数据轨迹同步化方法。首先基于离散小波变换分别对时段数据参考轨迹R和待同步化轨迹T进行多级的低频分解，然后将分解后的对应过程变量的节点系数组成系数矩阵，使用DTW 对参考轨迹和待同步化轨迹各个尺度下的系数矩阵进行同步化，最后利用离散小波逆变换得到同步化后的等长时段数据。以2级分解为例，如图2(a)所示，经过2级分解后，R和T分别得到3个频段系数矩阵：Rd1、Rd2、Ra2和 Td1、Td2、Ta2，每组频段系数矩阵对应一条同步化路径，如图2(b)所示，各个频段的同步化路径差异反映出两轨迹在各个频段中的差异性。

2 基于 LWPT-DTW 的不等长时段数据同步化

2.1 基于LWPT-DTW的不等长时段数据同步化

由于MSDTW方法仅仅对轨迹的低频部分进行多级分解，高频上的有用信息很容易被去掉，没有挖掘高频部分的有用信息，且使用离散小波变换在处理具有突变点的轨迹时会出现吉布斯现象，增加了轨迹的合成误差。为了充分提取轨迹在多尺度下的高低频信息，提高同步化结果的准确性，本文结合LWPT和DTW算法，提出一种基于LWPT-DTW的间歇过程不等长时段数据轨迹同步化方法。LWPT是基于提升方法的小波包变换[24]，不依赖于傅里叶变换，有效避免复杂的卷积运算和降低吉布斯现象的影响，运算快速且稳定，而且同时对高低频部分进行多级分解，可以对轨迹进行更精细的分析。参考轨迹R基于LWPT的分解过程如下：

（1）将 R根据奇偶性分解成采样时刻的偶次项Re和奇次项Ro

（2）基于数据相关性的基础上，用偶次项 Re去预测奇次项Ro，预测算子为P，令预测误差为

（3）通过预测误差 R1,0去调整 Re，更新算子为U，令调整后的Re为

经过上述步骤后，轨迹R完成了一级分解，得到高频分量R1,0和低频分量R1,1。分别对R1,0和R1,1重复以上的分解过程运算，获得轨迹R基于LWPT的多级分解结果，同理获得待同步化轨迹T基于LWPT的多级分解结果。LWPT的合成过程只需将分解等式的左右变量互换和改变符号的正负。

对R和T进行多级提升小波包分解，得到R和T不同频段的系数矩阵，利用DTW算法对频段系数矩阵进行同步化，通过提升小波包逆变换获得同步化后的等长时段数据，以2级分解的LWPT-DTW为例，如图2(c)所示，经过2级分解之后，R和T分别得到4个频段系数矩阵：R2,0、R2,1、R2,2和R2,3；T2,0、T2,1、T2,2和 T2,3，因此 LWPT-DTW方法可以获取4条同步化路径，如图2(d)所示。对比MSDTW方法， LWPT-DTW方法可以获得更多的频段系数矩阵和同步化路径，因此在相同的分解级数条件下，LWPT-DTW 方法可以更加充分提取原始轨迹的所有信息，而且可以更加精细地分析两轨迹在各个频段中的差异，因此基于 LWPT-DTW 的不等长时段数据轨迹同步化结果具有更高的准确性。

2.2 小波基函数和分解级数的选择

LWPT-DTW 轨迹同步化方法的参数是小波基函数和分解级数。本文针对在不同小波基函数和分解级数的设定下，根据最优同步化准确性，实现最优参数选择。选取PCA相似因子M判定同步化结果的准确性[25]，M由式（7）计算。

式中，R和T表示两条不等长时段数据的轨迹，λ表示协方差矩阵的特征值；θpq表示R的负载矩阵的第p个负载向量与T的负载矩阵的第q个负载向量的角度；A是主元个数。

M越大，同步化结果的准确性越高，考虑不同批次数据之间的差异性，定义一个平均同步化准确性指标G

其中，Mi是第i个批次的不等长时段的同步化准确性，I是批次总数。G的值越大，说明在当前的分解级数和小波基函数设定下，不等长时段的同步化结果具有更高的准确性和鲁棒性。

3 实验验证

青霉素是一种具有广泛临床医用价值的抗生素，其生产过程是一个典型的非线性、动态和多时段的间歇生产过程[26-27]。本文采用Pensim仿真平台[28]，为青霉素分批补料发酵过程提供仿真数据，选取的10个主要过程变量为：①通风率（L·h-1）、②搅拌功率（W）、③底物流加速率（L·h-1）、④基质浓度（g·L-1）、⑤溶氧量浓度（g·L-1）、⑥生物质浓度（g·L-1）、⑦青霉素浓度（g·L-1）、⑧培养基容量（L）、⑨二氧化碳浓度（g·L-1）、⑩反应热（kcal）。由Pensim仿真平台产生20个在不同初始条件设定下的批次过程数据。每批次的采样时间从380～420 h不等，采样间隔为1 h。为了反映实际生产过程不同批次的不确定性，所有过程变量均加入了高斯白噪声干扰。

基于K-均值聚类[29]算法将20个批次过程数据划分为3个时段，划分结果如图3所示。从图3中看出各个批次对应的时段数据存在不同步情况，因此需要对不等长时段数据进行同步化处理。分别利用DTW、MSDTW和LWPT-DTW对不等长时段数据进行同步化。设待同步化轨迹T经过上述3种同步化方法后得到的轨迹为T1、T2和T3，根据式（7）分别计算T与T1、T2、T3的相似性M。选择几种具有较好光滑性和相似性的小波基函数[30]，如表1所示。图4和表2分析了不同的小波基函数和分解级数组合对同步化结果准确性的影响。

表1 小波基函数Table 1 Wavelet base

图3 基于K-均值的时段划分Fig.3 Segmentation based K-means

图4展示了当分解级数分别为2和3时，选取不同的小波基函数对批次过程时段一平均同步化准确性的影响。从图中看出，在不同的小波基函数和分解级数的组合下，MSDTW 方法和 LWPT-DTW方法的平均同步化准确性有很大差异，甚至存在平均同步化准确性低于DTW方法的情况。当小波基函数选择bior2.4，分解级数为3时，平均同步化准确性最高，达到0.9990。表2列出了时段二和时段三的3种方法的平均同步化结果准确性，可以看出，对于时段二和时段三，当小波基函数选择bior2.4，分解级数为3时，平均同步化准确性最高。这是由于bior2.4小波基函数[31]具紧支撑性、双正交性和线性相位性等特性，采用一个小波函数进行轨迹分解，用另外一个小波函数进行合成，可以有效解决用同一个小波基函数进行分解与合成带来的对称性与合成信号准确性的矛盾问题，进而提高轨迹合成的准确性，因此本文选择的小波基函数为bior2.4以及分解级数设置为3。比较3种方法对所有训练批次不等长时段数据同步化的总耗时，其中DTW的总耗时为38.801 s，MSDTW方法总耗时为16.978 s，LWPT-DTW 方法的总耗时为 12.775 s。这是因为DTW算法中正向累积距离矩阵D的获取需要遍历R和T，MSDTW方法对R和T进行多尺度的低频部分分解，降低了数据计算量，LWPT-DTW方法中同时对高低频部分进行多尺度分解，且不依赖于傅里叶变换，避免复杂的卷积运算，因此LWPT-DTW方法具有更快的运算速度。基于 LWPT-DTW 对所有训练批次对应的不等长时段数据进行同步化，得到等长的时段。其中时段三的底物流加速率变量轨迹同步化结果如图 5所示，DTW、MSDTW 和LWPT-DTW 3种方法的同步化轨迹与原始轨迹的相似性分别为0.9550、0.9642和0.9764，LWPT-DTW方法的同步化结果具有更高的准确性，因此LWPT-DTW 方法在实现不等长时段数据同步化的情况下保留原始轨迹的更多信息。

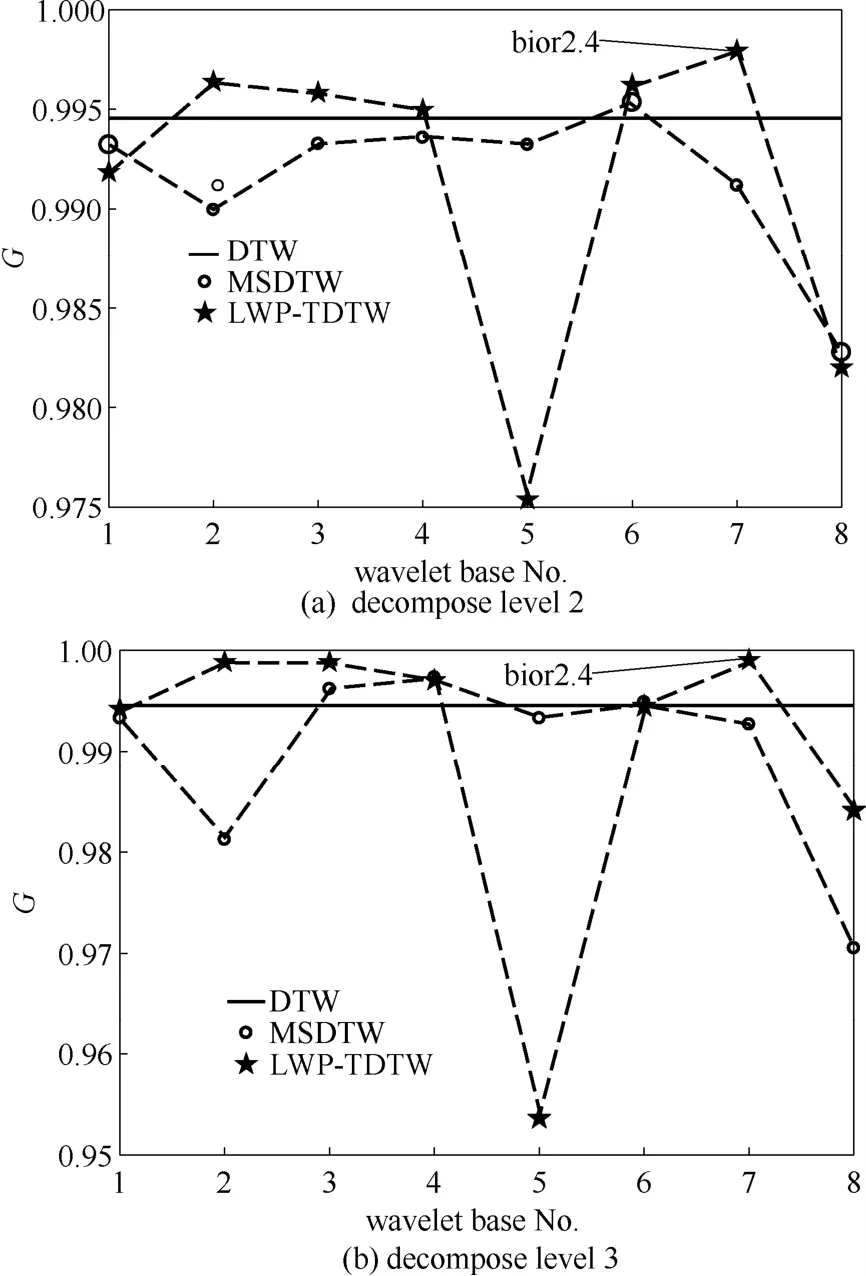
图4 3种方法的平均同步化结果准确性Fig.4 Mean synchronization accuracy of three methods

表2 3种方法的同步化准确性Table 2 Synchronization accuracy of three methods

图5 底物流加速率轨迹的同步化结果Fig.5 Synchronization of substrate feed rate trajectory

4 结 论

间歇过程具有多时段特性，同时间歇过程的不同批次对应时段的操作时间因生产原料的质量差异、初始条件的设置差异等出现不同步，导致各个批次对应时段的数据长度不一致。针对间歇过程不等长时段数据问题，提出一种基于 LWPT-DTW 的间歇过程不等长时段数据同步化方法，与DTW方法和MSDTW方法比较，LWPT-DTW方法对间歇过程不等长时段数据轨迹进行高低频的多级分解，可以充分提取数据轨迹的所有时频域信息，利用提升小波包逆变换对同步化后的系数矩阵进行合成，降低吉布斯现象对数据轨迹合成的影响，获得了间歇过程等长的时段。结合青霉素发酵过程进行了方法验证，实验结果表明，所提出的方法运算速度快、稳定，提高了间歇过程不等长时段数据同步化结果的准确性，能为间歇过程时段建模提供可靠的过程数据。

[1] YAN Z, HUANG B L, YAO Y. Multivariate statistical process monitoring of batch-to-batch startups [J]. AIChE Journal, 2015, 61(11)： 3719-3727.

[2] LUO L, BAO S, MAO J, et al. Phase partition and phase-based process monitoring methods for multiphase batch processes with uneven durations [J]. Industrial & Engineering Chemistry Research,2015, 55 (7)： 2035-2048.

[3] 王亚君, 孙福明. 基于多动态核聚类的间歇过程在线监控 [J]. 化工学报, 2014, 65 (12)： 4905-4913.WANG Y J, SUN F M. Multiple dynamic kernel clustering based online monitoring for batch processes [J]. CIESC Journal, 2014, 65(12)： 4905-4913.

[4] LV Z, YAN X, JIANG Q. Batch process monitoring based on just-in-time learning and multiple-subspace principal component analysis [J]. Chemometrics & Intelligent Laboratory Systems, 2014,137 (20)：128-139.

[5] DONG W W, YAO Y, GAO F R. Phase analysis and identification method for multiphase batch processes with partitioning multi-way principal component analysis (MPCA) model [J]. Chinese Journal of Chemical Engineering, 2012, 20 (6)： 1121-1127.

[6] HU Y, MA H, SHI H. Enhanced batch process monitoring using just-in-time-learning based kernel partial least squares [J]. Chemometrics& Intelligent Laboratory Systems, 2013, 123 (3)：15-27.

[7] ZHOU Z, WEN C, YANG C. Fault detection using random projections and k-nearest neighbor rule for semiconductor manufacturing processes [J]. IEEE Transactions on Semiconductor Manufacturing, 2015, 28 (1)： 70-79.

[8] WAN J, MARJANOVIC O, LENNOX B. Uneven batch data alignment with application to the control of batch end-product quality[J]. ISA Transactions, 2014, 53 (2)： 584-590.

[9] TAYLOR J, ZHOU X, ROUPHAIL N M, et al. Method for investigating intradriver heterogeneity using vehicle trajectory data： a dynamic time warping approach [J]. Transportation Research Part B：Methodological, 2015, 73 (2015)： 59-80.

[10] GONZÁLEZMARTÍNEZ J M, VITALE R, NOORD O E D, et al.Effect of synchronization on bilinear batch process modeling [J].Industrial & Engineering Chemistry Research, 2014, 53 (53)：4339-4351.

[11] KASSIDAS A, MACGREGOR J F, TAYLOR P A. Synchronization of batch trajectories using dynamic time warping [J]. AIChE Journal,1998, 44 (4)： 864-875.

[12] GONZÁLEZ-MARTÍNEZ J M, FERRER A, WESTERHUIS J A.Real-time synchronization of batch trajectories for on-line multivariate statistical process control using dynamic time warping [J]. Chemometrics and Intelligent Laboratory Systems, 2011, 105 (2)： 195-206.

[13] DAI C, WANG K, JIN R. Monitoring profile trajectories with dynamic time warping alignment [J]. Quality and Reliability Engineering International, 2014, 30 (6)： 815-827.

[14] BORK C, NG K, LIU Y, et al. Chromatographic peak alignment using derivative dynamic time warping [J]. Biotechnology Progress, 2013,29 (2)： 394-402.

[15] ZHANG Y, EDGAR T F. A robust dynamic time warping algorithm for batch trajectory synchronization[C]//2008 American Control Conference. IEEE, 2008： 2864-2869.

[16] ZHANG Y, LU B, EDGAR T F. Batch trajectory synchronization with robust derivative dynamic time warping [J]. Industrial & Engineering Chemistry Research, 2013, 52 (35)： 12319-12328.

[17] LI Y, WEN C L, XIE Z, et al. Synchronization of batch trajectory based on multi-scale dynamic time warping [C]//Machine Learning and Cybernetics, 2003 International Conference on. IEEE, 2003, 4：2403-2408.

[18] BARBON S, GUIDO R C, VIEIRA L S, et al. Wavelet-based dynamic time warping [J]. Journal of Computational and Applied Mathematics, 2009, 227 (2)： 271-287.

[19] LEE S, KIM J. Discrete wavelet transform-based denoising technique for advanced state-of-charge estimator of a lithium-ion battery in electric vehicles [J]. Energy, 2015, 83： 462-473.

[20] LI F, CHURCH G, JANAKIRAM M, et al. Fault detection for batch monitoring and discrete wavelet transforms [J]. Quality & Reliability Engineering International, 2011, 27 (8)：999-1008.

[21] WANG L, LI B, TIAN L F. Multi-modal medical image fusion using the inter-scale and intra-scale dependencies between image shift-invariant shearlet coefficients [J]. Information Fusion, 2014, 19： 20-28.

[22] LU B, XU S, STUBER J, et al. Constrained selective dynamic time warping of trajectories in three dimensional batch data [J]. Chemometrics and Intelligent Laboratory Systems, 2016, 159： 138-150.

[23] RAMAKER H J, SPRANG E N M V, WESTERHUIS J A, et al.Dynamic time warping of spectroscopic BATCH data [J]. Analytica Chimica Acta, 2003, 498 (1-2)：133-153.

[24] WANG Z, BIAN S, LEI M, et al. Feature extraction and classification of load dynamic characteristics based on lifting wavelet packet transform in power system load modeling [J]. International Journal of Electrical Power & Energy Systems, 2014, 62： 353-363.

[25] GUNTHER J C, BACLASKI J, SEBORG D E, et al. Pattern matching in batch bioprocesses-comparisons across multiple products and operating conditions [J]. Computers & Chemical Engineering,2009, 33 (1)： 88-96.

[26] YANG C, HOU J. Fed-batch fermentation penicillin process fault diagnosis and detection based on support vector machine [J].Neurocomputing, 2016, 190：117-123.

[27] LV Z, JIANG Q, YAN X. Batch process monitoring based on multisubspace multiway principal component analysis and time-series Bayesian inference [J]. Industrial & Engineering Chemistry Research,2014, 53 (15)： 6457-6466.

[28] BIROL G, ÜNDEY C, CINAR A. A modular simulation package for fed-batch fermentation： penicillin production [J]. Computers &Chemical Engineering, 2002, 26 (11)： 1553-1565.

[29] 张子羿, 胡益, 侍洪波. 一种基于聚类方法的多阶段间歇过程监控方法 [J]. 化工学报, 2013, 64 (12)： 4522-4528.ZHANG Z Y, HU Y, SHI H B. Multi-stage batch process monitoring based on a clustering method [J]. CIESC Journal, 2013, 64 (12)：4522-4528.

[30] LI S, WEN J. A model-based fault detection and diagnostic methodology based on PCA method and wavelet transform [J].Energy and Buildings, 2014, 68： 63-71.

[31] DHOKA M, KADAM J. Digital watermarking for medical images using biorthogonal wavelet filters and transformed watermark embedding [J]. International Journal of Advanced Computer Research,2014, 4 (2)： 705-712.

LWPT-DTW trajectory synchronization of uneven-length phase data in batch processes

WANG Jianlin, LIU Weimin, QIU Kepeng, ZHANG Weijia, YU Tao
(College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China)

Uneven-length phase data of batch processes directly affect phase modeling accuracy of data-driven multivariate statistical analysis, resulting in reduced process monitoring performance. A trajectory synchronization method of lifting wavelet package transform (LWPT) and dynamic time warping (DTW) was proposed for the uneven-length phase data of batch process. First, LWPT was used to decompose trajectories of uneven-length phase data at multiple levels of high and low frequency and extract complete time-frequency domain information.Secondly, DTW was used to synchronize coefficient matrices at different frequency bands. Finally, inverse LWPT was used to integrate synchronized coefficient matrices, to obtain the even-length phases, and to reduce the impact of the Gibbs phenomenon on data trajectory synthesis. The simulation results of penicillin fermentation batch process show that the new method calculates fast and stable with better accuracy of synchronization, which can provide reliable process data for data-driven phase modeling of batch processes.

uneven-length phase data; trajectory synchronization; lifting wavelet package transform; dynamic time warping; batch process

date：2016-12-02.

Prof. WANG Jianlin, wangjl@ mail.buct.edu.cn

supported by the National Natural Science Foundation of China (61240047) and the Natural Science Foundation of Beijing(4152041).

TQ 277

A

0438—1157（2017）07—2866—07

10.11949/j.issn.0438-1157.20161705

2016-12-02收到初稿，2017-04-21收到修改稿。

联系人及第一作者：王建林（1965—），男，教授。

国家自然科学基金项目（61240047）；北京市自然科学基金项目（4152041）。