基于Generalized LASSO模型的长江寸滩站年均径流突变研究
贺冉冉,陈元芳,黄 琴,吴 晶
(1. 河海大学水文水资源学院,江苏 南京 210098; 2.蚌埠学院材料与化学工程学院,安徽 蚌埠 233030)
基于Generalized LASSO模型的长江寸滩站年均径流突变研究
贺冉冉1,2,陈元芳1,黄 琴1,吴 晶1
(1. 河海大学水文水资源学院,江苏 南京 210098; 2.蚌埠学院材料与化学工程学院,安徽 蚌埠 233030)
为了区分水文时间序列的趋势和跳跃变异,将基于L1范数正则化技术的generalized LASSO模型应用于水文序列变异识别。经过识别,发现长江寸滩水文站年平均流量序列在1969年发生了向下的均值跃变。此外,趋势分析表明无论是跃变前后的子序列还是剔除跳跃成分的整个序列,均未检出显著的趋势,这说明对寸滩水文站年平均流量序列的跳跃变异假设是合理的。基于generalized LASSO模型的结果与其他突变检测方法结果进行比较,所得结论是一致的。
水文时间序列;变异识别;跳跃点;趋势分析;generalized LASSO;长江上游寸滩水文站
近几十年来,由于气候变化和人类活动引起下垫面性质的改变,导致了径流序列发生变异的可能性增大,这也使得对水文序列的变异分析成为水文时间序列分析的热点问题之一[1-2]。水文序列变异,是指水文变量的分布形式和分布参数随着时间发生了变化[2]。在对水文序列进行频率分析时,水文序列的非平稳性会导致计算结果的不确定性增加[3-4]。对水文序列的变异进行诊断可以使人们更深入地了解水文序列的变化规律,并能够合理地对未来变化趋势进行评估。
在多种类型的水文序列变异中,水文变量的均值水平发生变异是最基本的也是最重要的变异类型。水文序列的均值变异有2种可能的表现形式,即趋势或者跳跃。从函数逼近的角度来看,所谓的趋势是指可以用一个对时间的线性函数来描述均值水平随着时间的变化规律;而跳跃则是指可以用一个分段常数函数来描述均值的变化规律。区分这2种变异类型有着重要的意义,因为趋势相对于跳跃,更加肯定未来变异的持续性[5]。将历史水文序列诊断为趋势或者跳跃变异将会导致不同的外推结论。确定水文序列的变异是趋势还是跳跃得到一些研究者的重视[6]。
目前有许多水文序列变异识别方法。针对趋势识别,最常用的有Mann-kendall趋势检验;而针对跳跃点进行识别或检验的方法包括滑动t检验、有序聚类法、Pettitt检验等[7-9]。由于水文序列的复杂非线性特征和普遍不长的观测年份(一般为几十年),变异识别在应用中常将多种识别检验方法联用,例如通过综合的变异诊断系统来进行变异的识别检验[10]。多种方法联用可以降低结果的不确定性,这也说明开发新的有效的变异点识别方法是有益的。
LASSO(least absolute shrinkage and selection operator)是近年来应用较为广泛的变量选择方法[11],其原理是对回归系数的L1范数进行约束,可以将一部分系数收缩为0,进而获得稀疏的模型结构。Tibshirani等[12]提出的generalized LASSO是对LASSO的拓展,通过将不同类型的惩罚项表达成统一形式,不仅可以获得稀疏的模型结构,而且可以获得特定的模型结构特征。尽管generalized LASSO模型并未在水文时间序列变异检验中有过应用,但是与其相关的fused LASSO模型已经在水文时间序列突变点检验中有所应用[13]。笔者将基于generalized LASSO的识别方法引入水文序列变异的识别,其思路是将变异识别看作是对水文时间序列的函数逼近过程。将generalized LASSO模型应用于函数逼近时,通过对逼近序列构造特定的约束,可以获得一个分段常数逼近序列或者分段一次函数序列,通过调整正则化参数可以识别一系列可能的变异点。可以基于交叉验证技术根据最小的验证集误差来选择最优的正则化参数值,进而获得最优的分断逼近序列和其对应的变异点。此外,交叉验证误差还可以用来选择最优的假设,即是用分段常数序列还是线性函数序列来逼近水文序列,进而可以确定变异的类型是均值跳跃还是趋势变异。
本文首先叙述generalized LASSO模型的原理,并介绍其求解过程和交叉验证的方法,然后以长江上游寸滩水文站的年平均流量序列为例来探讨基于generalized LASSO的变异识别方法的应用。
1 Generalized LASSO原理
1.1 Generalized LASSO
LASSO模型的实质是在线性回归最小二乘法的基础上增加对系数绝对值之和(即系数向量的L1范数)的约束,用来对模型系数进行收缩,进而获得稀疏的模型。LASSO的原理可以参考相关文献[11],本文不再赘述。在LASSO被提出之后,出现了一些类似的同样是基于L1范数约束的扩展模型[14]。在这些模型中,通过修改模型L1范数的形式可以获得一系列特定的模型性质。Tibshirani[12]在2011年提出的generalized LASSO模型将多个不同类型的L1范数正则化问题封装成为同样的形式。Generalized LASSO模型应用于对水文序列的逼近时,其形式为
(1)
式中:y——长度为n年的水文序列,n×1矩阵;β——对序列y的逼近序列,n×1矩阵;D——某种形式的惩罚矩阵;λ——正则化参数。在式(1)中,通过选择某种类型的惩罚矩阵D,可以使Dβ的稀疏性与β的某种性质联系起来。
如果假设对水文序列逼近函数的形式为分段常数函数(即假设水文序列的变异类型为跳跃型),则式(1)中的矩阵D可以被设置为(n-1)×n矩阵D0:
(2)

(3)
式中:βj——β的第j个元素。也就是说,通过对β相邻元素之差的绝对值之和进行惩罚,可以获得对原序列y的阶梯函数逼近。在式(3)中,对逼近序列β跳跃点个数的控制通过设定λ来实现。当λ为0时逼近序列β与原序列相等,而当λ无穷大时逼近序列β为常数。在λ从0变为无穷大的过程中,β相邻的元素逐渐融合(即大小变得相等,β序列跳跃点逐渐消失)。这个模型被称为fused LASSO[14]。
如果假设逼近函数的形式为分段线性函数,则可以设置矩阵D为(n-2)×n矩阵D1:
(4)

(5)
因此,对D1β的惩罚就成了对β序列的离散二阶导数的绝对值之和进行惩罚,而所获得的逼近序列β就是分段线性函数。在一些文献中,这个过程被称为趋势滤波[15]。
1.2 求解方法
对(1)式的求解,选取不同的λ值会有不同的解β,可以通过所谓求解路径的方法来求解所有λ值对应的解。以fused LASSO问题为例[12],求解思路是首先将原问题转化为对偶问题进行求解:
(6)
式中:u——拉格朗日乘子。
可以证明对于任意的λ,原问题和对偶问题的解存在如下的关系:
(7)
式中:βλ——正则化参数取值为λ时对应的解;uλ——正则化参数取值为λ时对应的拉格朗日乘子。
所谓的求解路径,就是依次求解λ从变化到0的所有值对应的解。由于对偶问题的解向量uλ在λ的变化过程中是分段线性变化的,也就是λ在相邻拐点的区间内部变化时,uλ路径的方向是不变的,而变化只发生在若干个拐点之处。由于式(7)的关系,可以知道βλ也是分段线性变化的。这样只需要给出λ在若干关键节点处对应的解βλ,即完成了整个求解路径的求解。矩阵D取值为D0和D1时求解方法的证明过程以及计算程序可以参考相关文献[12]。
1.3 交叉验证方法
交叉验证的目的是为了评估假设的合理性和选择最优的λ值,其程序简述如下[12]。交叉验证首先需要对样本进行分类,其方法是循环将时间序列元素依次编入指定的类别。具体来说,假设序列的长度为8,记为y1,…,y8,进行3折交叉验证,将样本类别记为c1、c2、c3,则将样本依次循环编入指定类别:y1(×),y2(c1),y3(c2),y4(c3),y5(c1),y6(c2),y7(c3),y8(×),其中两端括号中的×表示两端的元素(即y1和y8)不归入任何类别,始终作为交叉验证时建模的训练样本。在进行交叉验证时,如需将c2类中的样本作为测试集,只需将其余2类样本(也包括两端的样本)作为训练集,对指定的λ计算逼近序列。任意一个c2类样本点的预测值都可以通过相邻的点(因为肯定不在c2类中)的逼近值取平均求出。这样,通过计算不同λ产生的逼近序列在测试集上的误差,可以作为选择最优λ值的参考。笔者在交叉验证时选择进行10折交叉验证。

图1 寸滩站年平均流量序列及多年均值水平Fig.1 Annual mean streamflow series at Cuntan station and multi-year mean value
1.4 计算的软件实现
本文的所有计算和绘图都是在R语言的环境下进行的,其中对generalized LASSO模型的求解和交叉验证使用了R语言扩展包genlasso[16]。
2 实 例 分 析
2.1 基于generalized LASSO的寸滩站年平均径流量序列的变异识别
以长江上游重要控制站寸滩站1893—2012年的年平均径流量序列(图1)为例,对其进行变异类型的确定和变异点的识别和检验。从图1可见,20世纪60年代以来,年平均流量总体上处于历史平均水平之下。
在求解generalized LASSO模型时,不同的λ值对应着不同的逼近序列。较大的λ对应的逼近序列较为粗糙,而较小的λ对应的逼近序列则较为细致。图2分别给出了逼近多项式阶数为0(即分段常数函数)和阶数为1(即分段线性函数)时求解路径中最大的3个λ所对应的逼近序列,其对应的变异点数量分别为0个、1个和2个。从图2可见,随着正则化参数的减小,变异点的个数在逐渐增加。这些变异点可以作为具有优先次序的潜在变异点。

图2 求解路径中最大的3个λ值对应的逼近序列及对应的变异点位置Fig.2 Approximation series and change points corresponding to three maximum values of λ in solution path
如果限制变异点的个数为1个,对应于阶数为0的情况,在1969年出现了一个向下的跳跃点(图2(c));对应于阶数为1的情况,则在1955年出现了趋势转折(图2(d)),在其之后径流的下降速率明显增大。当减小正则化参数λ的值,出现2个变异点时,在跳跃变异的假设下会检出1927年出现了微弱的向下跳跃(图2(e));而在趋势转折的假设下(图2(f)),在1934年会出现趋势转折,从1934—1955年有短期的上升趋势。
考虑到过多的变异点难以通过统计检验验证,结合图2的信息,主要考虑3种备选的变异假设,分别称为假设A(全局趋势,见图2(b))、假设B(1955年为转折点的趋势变异,见图2(d))和假设C(1969年为跳跃点的均值变异,见图2(c))。
2.2 通过交叉验证来判断变异类型
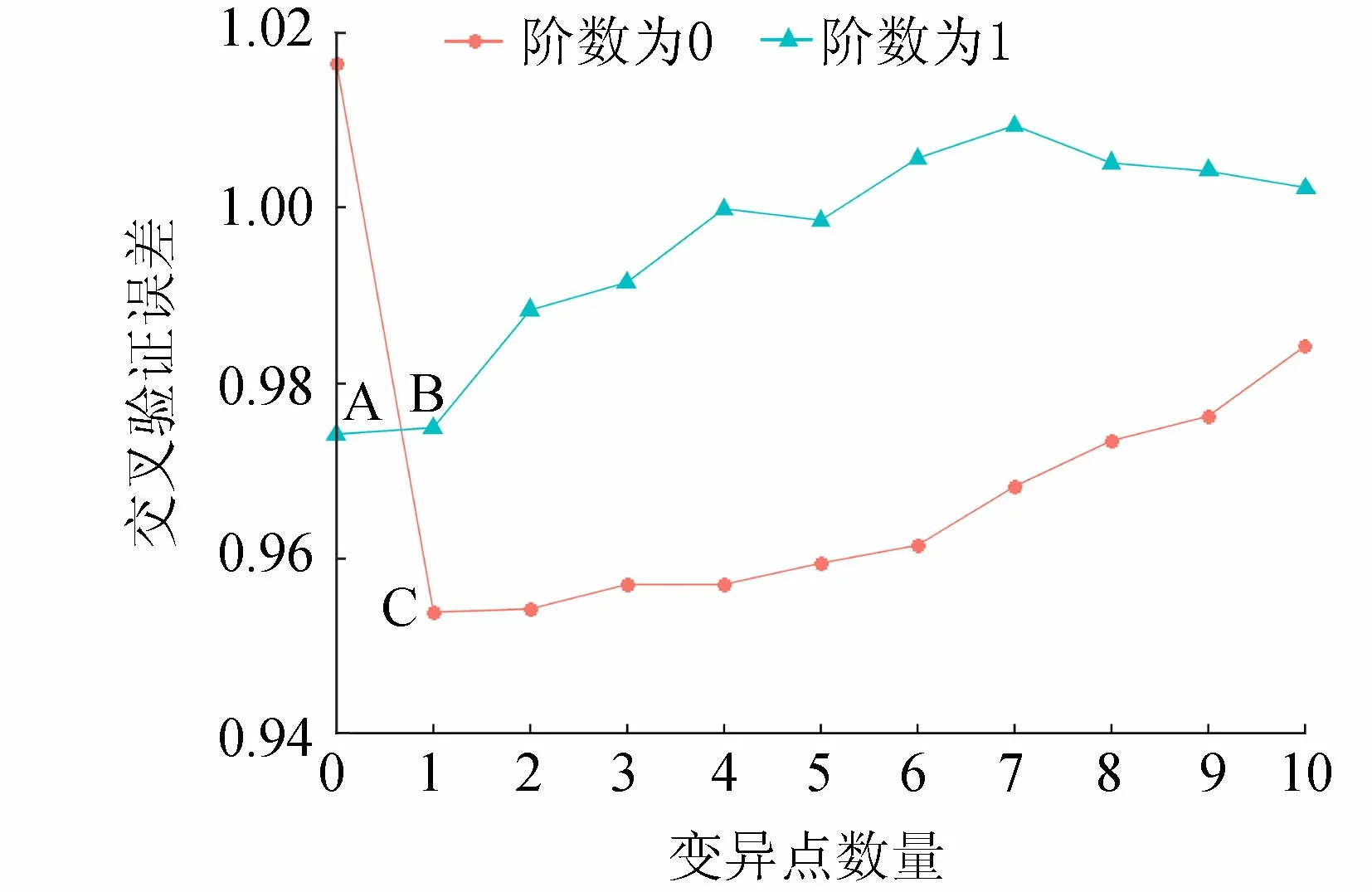
图3 不同变异点数量对应的交叉验证误差Fig.3 Cross-validation errors corresponding to different numbers of change points
如1.3节所述,为了确定寸滩年平均流量序列的变异类型,需要进行交叉验证。笔者同时给出了多项式阶数为0和1时,不同变异点个数对应的交叉验证误差(均方误差),见图3。在图3中,标注了2.1节中所述假设A、假设B和假设C对应的点。考虑到较大的变异点个数没有实际意义,在图3中只显示变异点个数小于等于10的情况。在计算交叉验证误差之前,首先将流量序列标准化处理为无量纲数,这样图3中的交叉验证误差也是无量纲的。
从图3中可以看出,在变异点个数为0的情况下,阶数为1相对于阶数为0来说有着明显小的交叉验证误差,说明相对于无均值变异的假设来说,全局的线性趋势假设是个更优的假设。但是从变异点数量从1到10来看,0阶逼近相对于1阶逼近一直有着较小的误差。其中在变异点个数为1的0阶逼近(即假设C)取得了最小的误差。这说明了存在一个均值跳跃点的分段常数函数逼近是最优逼近,也就是说,交叉验证的结果支持一个跳跃点变异的假设。
2.3 对整个序列及子序列的趋势检验
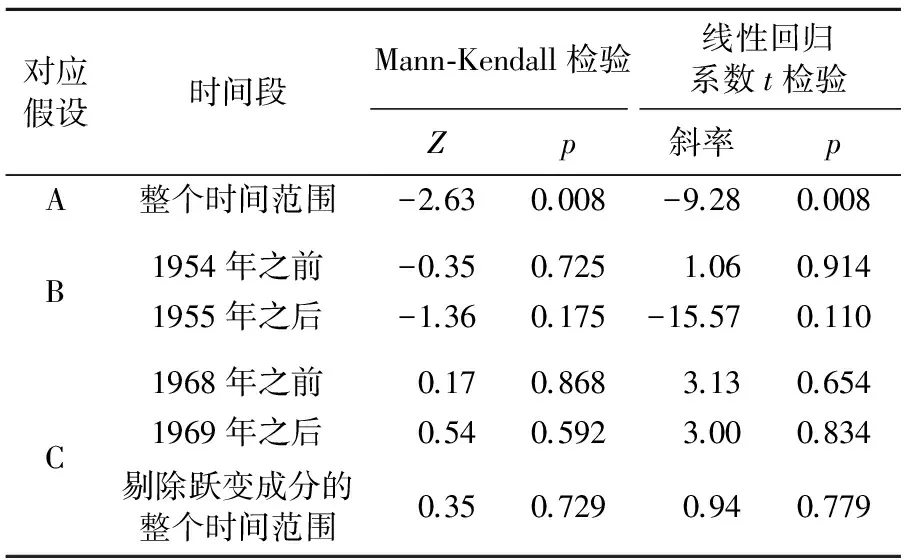
表1 对整个序列及子序列的趋势检验
为了进一步考察上述3种假设的合理性,以上面3种变异类型为基础,分别对子序列和整个序列的趋势进行Mann-Kendall检验和线性回归趋势检验,结果见表1。表1中Z值是Mann-Kendall检验的标准化统计量。从表1可以看出,检验整个时间范围(1893—2012年)时,2种趋势检验方法都表明有显著下降的趋势(p<0.01),这样假设A就无法排除。如果检验假设B的趋势转折变异点前后的子序列,则都没有显著的趋势,说明假设B不合理,即序列没有发生趋势转折。对于假设C,分别检验跳跃点前后的子序列和剔除跃变成分后的整个序列,都没有发现显著的趋势存在,这与假设C不矛盾。这样,通过一系列趋势检验,假设B就被排除,剩下假设A和假设C这2种竞争性的假设。
从上面的分析可以看出,趋势检验无法在2种竞争性的假设(即全局线性下降的趋势和一个跳跃点的变异)之间进行选择,这是因为其没有能力区分跳跃和趋势这2种变异类型[6],而上述的基于generalized LASSO的交叉验证技术可以在一定程度上提供另外的证据。
2.4 与其他跳跃点识别方法的对比
为了与其他的跳跃点识别检验方法相对照,笔者进行了4种突变点识别检验(即有序聚类法、滑动t检验法、Pettitt检验和累积距平法)。在进行滑动t检验时,依次选择1903—2002年作为分割点,将其前后序列作为2个样本进行t检验。结果表明所有的方法都给出了一致的结论,即1969年寸滩年平均流量发生了向下均值跃变。其中滑动t检验和Pettitt检验表明检出的变异在0.01水平上是显著的。这说明基于generalized LASSO模型识别出的跳跃点(假设C)是合理的。
3 讨论与结论
关于长江上游寸滩站的径流变异特征,已经有多个文献的研究所涉及。王顺久[17]通过线性趋势分析和Mann-Kendall检验得出寸滩的年径流存在显著下降的趋势。夏军等[18]也通过Mann-Kendall检验发现寸滩站年径流下降的趋势,并且通过累积距平法发现寸滩站年径流在1968年之前增加,而在1993年之后减小。根据李林等[19]的研究,长江上游河流可以认为是雨水补给型河流,降水是影响径流最主要的因素。冯亚文等[20]指出,长江上游的年径流量呈现减少的趋势,并且造成这种现象的主要原因仍是降水。夏军等[18]也指出气候变化是导致寸滩站径流发生了变异的主要因素。根据相关的研究及笔者的分析,寸滩站年径流量确实在近几十年是减小的,而难点在于如何评估其变异类型。如前所述,现今主流的趋势分析方法并不能区分全局趋势和跳跃变异,所以即使趋势检验的结果给出了显著变异的结论,寸滩年平均流量序列是否存在全局性趋势仍然是值得商榷的。本文通过多种方法的对比研究,认为寸滩站年平均流量序列呈现向下的跳跃变异。考虑到径流序列的随机性,这个结果还存在着一定的不确定性,而且其物理机制还需要深入研究。
需要指出的是,趋势分析和突变分析经常被同时使用。尽管多种方法联用可以增加结果的全面性,但是趋势和跳跃之间存在的逻辑关系却是一个需要厘清的问题,而这个问题在以往的研究中并未得到重视。如前所述,趋势是指均值在整个时间段内均值缓慢的变化,而跳跃突变是指均值在跳跃点前后从一个均值状态变为另一个状态。尽管由于水文序列的长度较短、噪声较大导致区分这2种变异类型有难度,但是在逻辑上,这2种结论是不相容的。以本文对寸滩流量的分析为例,当检测出跳跃点时,即表明全局趋势检验的结果已经受到跳跃点的干扰,所以需要对跳跃点前后的子序列或者是去除跳跃成分的整个序列重新进行趋势检验。这种先进行跳跃点检验再进行趋势检验的方法被一些文献所强调[21]。此外,还需要强调的是,对跳跃点前后子序列的趋势检验也是对跳跃点检验程序前提的验证,例如滑动t检验假设分割点前后的序列值来自于2个随机样本,也就是说分割点前后序列的均值应该是平稳的。
从方法上说,基于generalized LASSO模型的水文变异识别方法的有效性还需要进一步探讨。需要强调的是,由于水文序列的长度较短,并且存在较大的噪声,根据最小化交叉验证误差获得的逼近序列可能存在过拟合现象,所以其识别的变异点应该作为“可能的变异点”,最终还需要通过统计检验来对其进行确认。总之,generalized LASSO 模型可作为水文时间序列可能变异点的识别程序,其识别的潜在变异点可以作为后续统计检验的参考。
[ 1 ] MILLY P, JULIO B, MALIN F, et al. Stationarity is dead: whither water management?[J]. Ground Water News & Views, 2007, 4(1): 6-8.
[ 2 ] 谢平, 许斌, 刘媛, 等. 水资源序列变异的时间尺度主因分析方法[J]. 水力发电学报, 2013, 32(6): 24-30. (XIE Ping, XU Bin, LIU Yuan, et al. Key factor analysis of alteration in the hydrological series on time scale[J]. Journal of Hydroelectric Engineering, 2013, 32(6): 24-30.(in Chinese))
[ 3 ] 胡义明, 梁忠民, 赵卫民, 等. 基于跳跃性诊断的非一致性水文频率分析[J]. 人民黄河, 2014, 36(6): 51-53. (HU Yiming, LIANG Zhongmin, ZHAO Weimin, et al. Study on frequency analusis method of non-stationary observation based on jump analysis[J]. Yellow River, 2014, 36(6): 51-53.(in Chinese))
[ 4 ] 谢平, 陈广才, 夏军. 变化环境下非一致性年径流序列的水文频率计算原理[J]. 武汉大学学报(工学版), 2005, 38(6): 6-9. (XIE Ping, CHEN Guangcai, XIA Jun. Hydrological frequency calculation principle of inconsistent annual runoff series under Changing environments[J]. Engineering Journal of Wuhan University, 2005, 38(6): 6-9.(in Chinese))
[ 5 ] MCCABE G J, WOLOCK D M. A step increase in streamflow in the conterminous United States[J]. Geophysical Research Letters, 2002, 29(24): 38-1-38-4.
[ 6 ]ROUG C, GE Yan, CAI Ximing. Detecting gradual and abrupt changes in hydrological records[J]. Advances in Water Resources, 2013, 53(53): 33-44.
[ 7 ] 周园园, 师长兴, 范小黎, 等. 国内水文序列变异点分析方法及在各流域应用研究进展[J]. 地理科学进展, 2011, 30(11): 1361-1369. (ZHOU Yuanyuan, SHI Changxing, FAN Xiaoli, et al. Advances in the research methods of abrupt changes of hydrologic sequences and their applications in drainage basins in China[J]. Progress in Geography, 2011, 30(11): 1361-1369.(in Chinese))
[ 8 ] 孙东永,黄强, 王义民,等. 滑动近似熵在径流序列突变性分析中的应用[J]. 水力发电学报, 2014, 33(4): 1-6. (SUN Dongyong, HUANG Qiang, WANG Yimin, et al. Application of moving approximate entropy to mutation analysis of runoff time series[J]. Journal of Hydroelectric Engineering, 2014, 33(4): 1-6.(in Chinese))
[ 9 ] 李彬彬, 谢平, 李析男, 等. 基于Hurst系数与Bartels检验的水文变异联合分析方法[J]. 应用基础与工程科学学报, 2014, 22(3): 481-491. (LI Binbin, XIE Ping, LI Xi’nan, et al. Joint analysis method for hydrological variation based on Hurst coefficient and Bartels test[J]. Journal of Basic Science and Engineering, 2014, 22(3): 481-491.(in Chinese))
[10] 谢平, 陈广才, 雷红富, 等. 水文变异诊断系统[J]. 水力发电学报, 2010, 29(1): 85-91. (XIE Ping, CHEN Guangcai, LEI Hongfu, et al. Hydrological alteration diagnosis system[J]. Journal of Hydroelectric Engineering, 2010, 29(1): 85-91.(in Chinese))
[11] TIBSHIRANI R. Regression shrinkage and selection via the lasso: a retrospective[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2011, 73(3): 273-282.
[12] TIBSHIRANI R J, TAYLOR J. The solution path of the generalized lasso[J]. Annals of Statistics, 2011, 39(3): 1335-1371.
[13] JEON J J, SUNG J H, CHUNG E S. Abrupt change point detection of annual maximum precipitation using fused lasso[J]. Journal of Hydrology, 2016, 538:831-841.
[14] TIBSHIRANI R, SAUNDERS M, ROSSET S, et al. Sparsity and smoothness via the fused lasso[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2005, 67(1): 91-108.
[15] KIM S J, KOH K, BOYD S, et al. L1 Trend Filtering[J]. SIAM Review, 2009, 51(2): 339-360.
[16] ARNOLD T B, TIBSHIRANI R J. Genlasso: path algorithm for generalized lasso problems[EB/OL]. [2014-09-15]. https://CRAN.R-project.org/package=genlasso.
[17] 王顺久. 长江上游川江段气温、降水及径流变化趋势分析[J]. 资源科学, 2009, 31(7): 1142-1149. (WANG Shunjiu. Changing pattern of the temperature, precipitation and runoff in Chuanjiang section of the Yangtze River[J]. Resources Science, 2009, 31(7): 1142-1149.(in Chinese))
[18] 夏军, 王渺林. 长江上游流域径流变化与分布式水文模拟[J]. 资源科学, 2008, 30(7): 962-967. (XIA Jun, WANG Miaolin. Runoff changes and distributed hydrologic simulation in the upper reaches of Yangtze River[J]. Resource Science, 2008, 30(7): 962-967.(in Chinese))
[19] 李林, 王振宇, 秦宁生, 等. 长江上游径流量变化及其与影响因子关系分析[J]. 自然资源学报, 2004, 19(6): 694-700. (LI Lin, WANG Zhenyu, QIN Ningsheng, et al. Analysis of the relationship between runoff amount and its impacting factor in the upper Yangtze River[J]. Journal of Natural Resources, 2004, 19(6): 694-700.(in Chinese))
[20] 冯亚文, 任国玉, 刘志雨, 等. 长江上游降水变化及其对径流的影响[J]. 资源科学, 2013, 35(6): 1268-1276. (FENG Yawen, REN Guoyu, LIU Zhiyu, et al. rainfall and runoff trends in the upper Yangtze River[J]. Resources Science, 2013, 35(6): 1268-1276.(in Chinese))
[21] LI Dingfang, XIE Huantian, XIONG Lihua. Temporal change analysis based on data characteristics and nonparametric test[J]. Water Resources Management, 2014, 28(1): 227-240.
Abrupt change of annual mean streamflow at Cuntan Station on Yangtze River based on generalized LASSO
HE Ranran1,2, CHEN Yuanfang1, HUANG Qin1, WU Jing1
(1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China; 2.SchoolofMaterialandChemistryEngineering,BengbuUniversity,Bengbu233030,China)
In order to distinguish trends and abrupt changes in hydrological time series, the generalized LASSO model based on L1-norm regularization was used to detect changes in hydrological series. It is found that the annual mean streamflow series at the Cuntan Station shows a downward step change in 1969. Furthermore, trend analysis shows that both the sub-series before/after 1969 and the whole series after removing step change components show no significant trend, indicating that the assumption of the step change in the annual mean streamflow series at the Cuntan Station is reasonable. The conclusions obtained from the generalized LASSO method are consistent with those obtained from other change detection methods.
hydrological time series; change detection; jump point; trend analysis; generalized LASSO; Cuntan Station in upper reaches of Yangtze River
10.3876/j.issn.1000-1980.2017.04.012
2016-07-23
国家自然科学基金(51479061)
贺冉冉(1983—),男,安徽蚌埠人,讲师,博士研究生,主要从事水文不确定性分析。E-mail:heranran2006@163.com
P333
A
1000-1980(2017)04-0358-07

