基于卫星测高数据的海底地形反演及分析

眭晓虹 张润宁 万晓云 李洋

(1 航天东方红卫星有限公司，北京 100094) (2 钱学森空间技术实验室，北京 100094) (3 北京空间飞行器总体设计部，北京 100094)



基于卫星测高数据的海底地形反演及分析

眭晓虹1,2张润宁3万晓云2李洋1

(1 航天东方红卫星有限公司，北京 100094) (2 钱学森空间技术实验室，北京 100094) (3 北京空间飞行器总体设计部，北京 100094)

由于受限于观测条件，海底地形模型在分辨率与精度两方面较陆地和大地水准面模型有很大的差距。传统的海底地形测量是利用声呐船测技术获取水深数据，但该测量方法测量效率低、测量点分布稀疏不均匀。文章详细研究并推导了基于卫星测高数据进行海底地形反演的方法，采用卫星测高重力异常数据和少量船测水深数据，对北太平洋部分区域进行了海底地形反演，得到1′×1′分辨率的海底地形模型，并对反演关系中的非线性项进行了分析。仿真结果验证了此方法的可行性，指出海底地形与重力异常数据在一定波段内以线性关系为主，叠加非线性二次项和三次项可较好地提升反演精度，高于三次项的部分对反演的结果没有明显的作用，可以忽略。

海底地形；卫星测高；重力异常；声呐船测技术

1 引言

海底地形是描述海洋水下固体表面起伏的物理概念，对海底地形的精确探测不仅对研究地球物理科学具有重大的意义，同时对潜艇水下导航等军事活动、海底管线铺设等经济活动都具有指导作用[1-2]。在传统的海洋测绘中，声呐船测技术是获取测量船到海底地形起伏面的深度(即水深)数据的核心手段。利用测量船搭载声呐技术测量水深具有精度高的优点，但缺点是效率低、测量点分布稀疏不均匀，无法有效地实现高分辨率、高精度、全球化海底地形的探测。

自20世纪70年代发射第一颗搭载雷达高度计的测高卫星起，应用卫星测高技术获取全球海洋大地水准面高的数据变为了可能[3-5]。大地水准面作为最接近全球平均海面的重力场等势面，其形状反映了地球内部物质构造、密度及分布等信息，与海底地形在一定程度上具有高相关性[6]。Dixon、Ramillien、Hwang、黄谟涛等多名国内外研究人员基于卫星测高数据提取海面重力测量数据，并对部分海域进了海底地形反演[7-10]，但这些反演过程只考虑海面重力数据与海底地形线性相关性，对于非线性的相关程度未予考虑。

本文基于Smith&Sandwell(S&S)的经典方法[1]，系统探讨了应用卫星测高数据进行海底地形反演的方法，并进行了仿真分析。仿真结果表明，基于S&S方法可以有效地反演海底地形。针对前人忽略的反演关系中非线性项部分，文中亦做了仿真分析，结果表明，海底地形与重力异常数据在一定波段内以线性关系为主，叠加非线性二次项和三次项可较好地提升反演精度，高于三次项的部分对反演的结果没有明显的作用。

2 卫星测高数据反演海底地形的原理及方法

2.1 卫星测高数据计算海洋重力异常

基于Sandwell方法，可从卫星测高数据得到沿轨海面高程斜率，结合测高点的位置和时间信息得到沿轨大地水准面起伏对空间的导数，从而计算海面垂线偏差。如图1所示，以相对于平均海面z0深度的参考水深面作xy平面建立直角坐标系，x轴指向地理东向，y轴指向地地理北向，z轴与x和y轴构成右手坐标系。记海面东向和北向垂线偏差的分量分别为

(1)

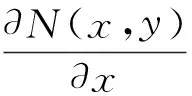
(2)

式中：N(x,y)表示点(x,y)处大地水准面高度，即大地水准面与参考椭球面的距离差。

图1 平均海面与海底地形坐标示意图Fig.1 Coordinate system for mean sea surface and sea floor topography

根据逆Vening-Meinesz公式，可由垂线偏差计算海洋重力异常Δg[11]为

η(P)sinα]dσ

(3)

式中：g0为海平面的重力加速度，通常取9.8m·s-2；ξ(P)和η(P)分别为P处垂线偏差的北向和东向分量；α为流动点至测量点的方位角；H′(ψ)为积分核函数。

(4)

式中：ψ为流动点到计算点的球面角距。

至此，已建立测高数据与海洋重力异常的相互关系。根据物理大地测量学相关理论，海底地形起伏变化将引起局部重力场扰动，记为扰动重力δg，该重力场扰动包含于海洋重力异常。针对重力异常数据在相关波段内滤波，保留与海底地形具有高相关性的扰动重力，才可进而反演海底地形。

2.2 利用扰动重力反演海底地形

假设存在z=h(r)的一个海底地形起伏面，如图1所示，h(r)为相对于参考水深面的海底地形高度。图中海面上P点处海底地形产生的扰动位记为

(5)

式中：G=6.672 6×10-11Nt·m2·kg-2为地球引力常数；r0和r分别为计算点的位置矢量和海底地形起伏面z=h(r)的流动体元的位置矢量；Δρ为海底固体岩石层与海水的密度差。

采用频域分析法，较之经典的时域分析法可以快速地体现系统的响应过程，高效率地计算得到系统响应输出，并为相关波段的截取提供便利。将式(5)在z=z0平面内进行二维傅里叶变换可快速得到

(6)

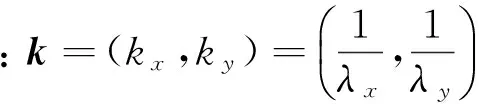
海面扰动重力是重力扰动位U(r0)在垂直方向上的导数，计算式(6)并根据傅里叶变换的性质可得频域内扰动重力δg的表达式：

F[δg]=|k|F[U(r0)]=

(7)

根据式(7)即可利用扰动重力δg数据反演海底地形高度h(r)[1,12-13]。

2.3 反演方法

本文基于式(7)，利用规则的卫星测高重力异常数据结合稀疏的船测水深数据反演海底地形。对测高重力异常数据在与海底地形有高相关性的波段进行滤波，得到扰动重力。文中以部分船测点作为控制点，将控制点处的水深数据作为真实水深数据，滤除与扰动重力相关性差的长波水深数据得到残余水深。以船测残余水深数据与船测航迹上的扰动重力建立相关关系，得到只考虑一阶项的线性系数和考虑多阶项的非线性系数。在船测航迹之外的区域，将得到的线性和非线性系数叠加到扰动重力的作用中，从而得到非船测航迹处预测水深。结合预测水深数据与长波水深数据，即可得到计算区域内的全波段水深，即海底地形。将未参与计算的船测点作为外部校核点，用以衡量海底地形的反演精度。

3 数据准备

仿真实验针对区域40°N～50°N，150°E～160°E的北太平洋海域内，基于一组卫星测高重力异常数据进行海底地形反演，并应用一组稀疏船测水深数据作为控制点辅助仿真。重力异常数据来源于丹麦科技大学空间研究所，数据分辨为1′×1′，数据总点数为361 201，该数据由多年的测高卫星数据计算得到，数据如图2所示。

图2 重力异常数据Fig.2 Gravity anomalies data

稀疏船测数据来源于美国大气海洋管理局(NOAA)，船测数据总点数为57 986。稀疏船测水深数据(如图3所示)表示测量船(海面)到海底地形起伏面的深度，取向上为正。

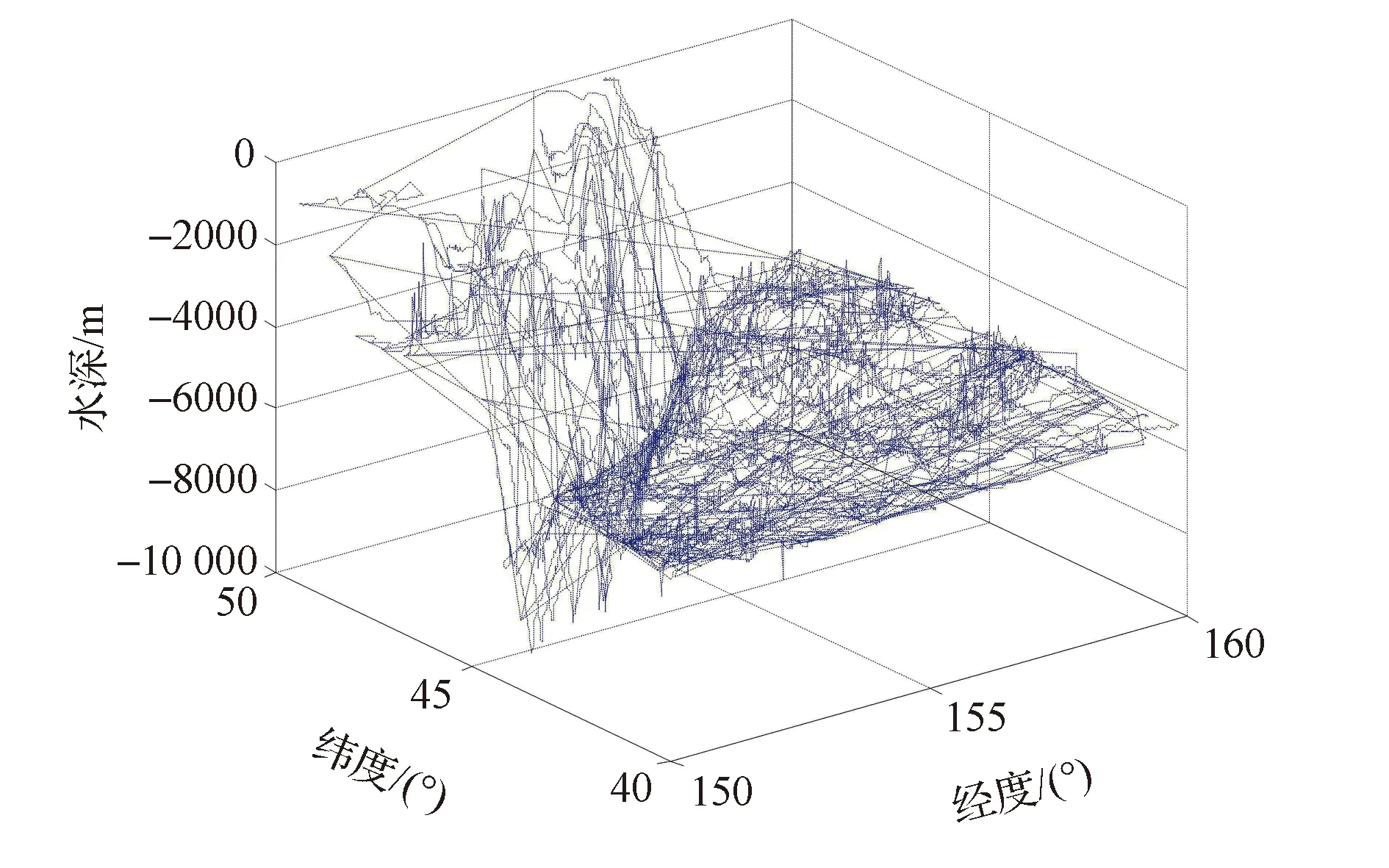
图3 船测水深数据(图中包含测量船的航迹线)Fig.3 Shipboard bathymetry data(with survey ship routes)

文中取56 826个船测数据点作为控制点带入海底地形反演的计算，数据点分布如图4所示。

图4 船测水深控制点数据(无船测航迹线)Fig.4 Shipboard bathymetry data of reference points(without survey ship routes)

其余1160个船测数据点作为核验点带入海底地形反演精度的核验，数据点分布如图5所示。

图5 船测水深核验点数据Fig.5 Shipboard bathymetry data of check points

针对船测水深数据中部分数据偏差较大的情况，需要对船测水深数据进行粗差校正。为了方便粗差校正，并滤除长波水深数据，首先对不规则的船测水深数据插值得到格网化的原始船测水深，如图6所示；经过粗差校正后的水深数据如图7所示，从图6与图7的对比可看出，粗差校正有效地剔除船测水深中偏差较大的数据，从而提高仿真实验的数据可信性。

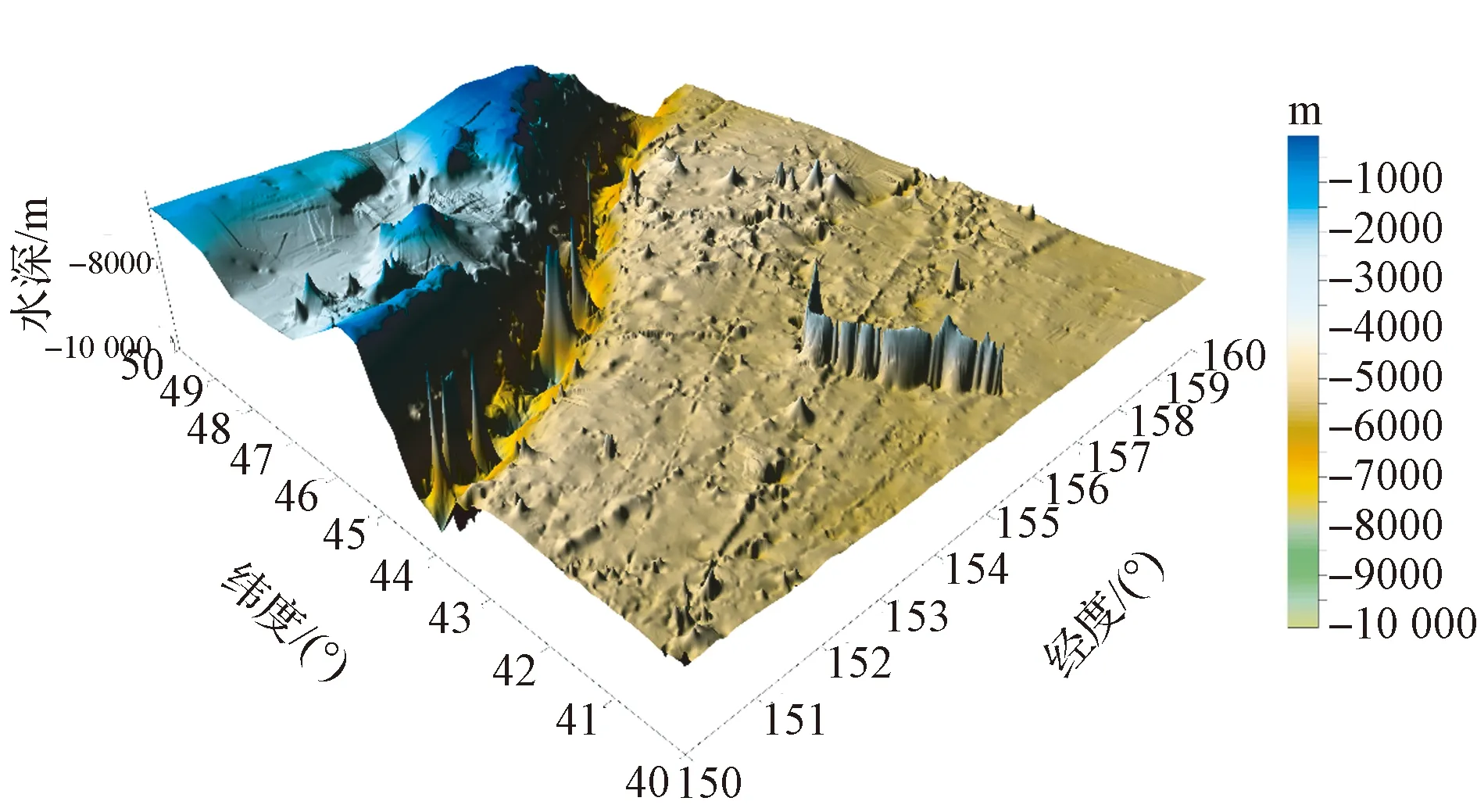
图6 船测水深格网化后的三维图像Fig.6 3D presentation for gridded shipboard bathymetry

图7 粗差校正后的船测水深三维图像Fig.7 3D presentation for gridded shipboard bathymetry after cross error correction

4 仿真分析

仿真基于文中第2节的反演原理和方法，利用第3节的实验准备数据进行仿真实验，具体的仿真流程如图8所示。

图8 仿真实验流程图Fig.8 Flow chart for simulation

根据重力异常与水深在海底地形波长为20～200 km波段内具有高相关性的理论，对船测水深数据进行低通滤波，滤波器设计如图9所示，可获得波长大于200 km的长波船测水深数据，如图10所示(图中将船测水深转化为地形高度)；同时对重力异常数据进行带通滤波，滤波器设计如图11所示，可获得波长介于20 km与200 km之间的扰动重力数据并向下延拓至参考水深处(文中参考水深为z0=4 km)，如图12所示。

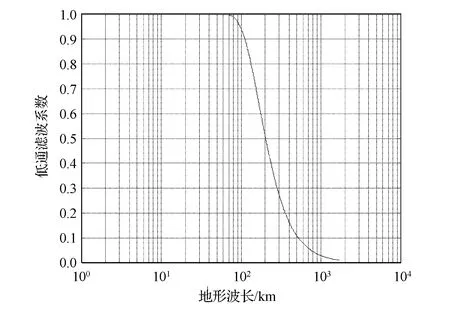
图9 低通滤波器Fig.9 Low pass filter

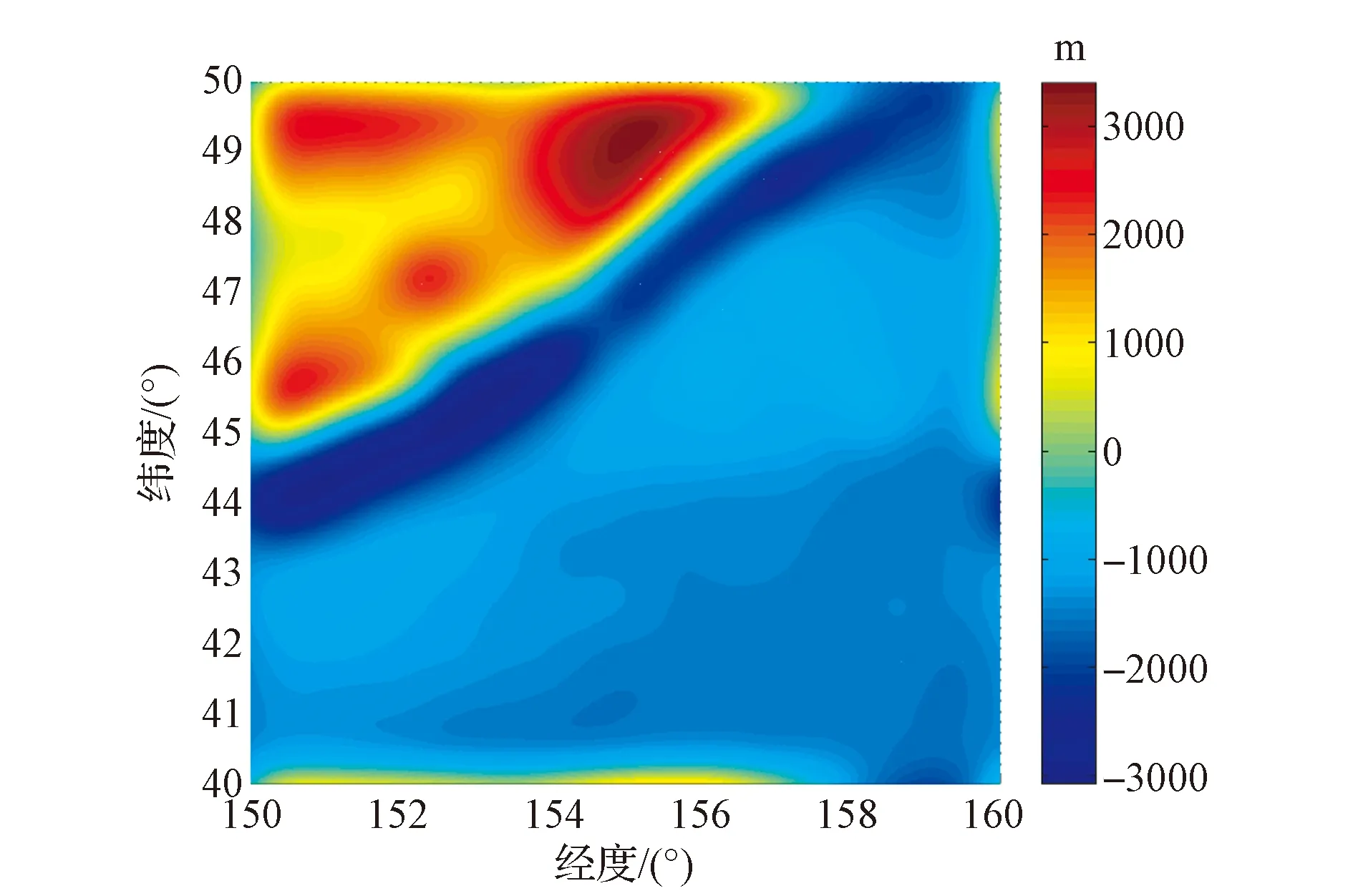
图10 长波船测海底地形数据Fig.10 Long wavelength shipboard bathymetry

图11 带通滤波器Fig.11 Band pass filter

针对船测残余水深数据与20～200 km的船测航迹上的扰动重力数据进行回归分析并均匀插值，得到船测航迹上海底地形与扰动重力的线性系数和多阶非线性系数。将仿真区域的扰动重力与相关系数相乘即可得到短波水深数据，将计算水深与长波水深相加即可得到全区域的反演水深。

图12 带通滤波并向下延拓至参考水深处的扰动重力数据Fig.12 Gravity anomaly disturbance data being band pass filtered and downward continued to reference water depth

经过计算，最终得到1′×1′的海底地形模型。图13所示为仅考虑一阶线性项的海底地形反演结果，地形高度以相对于参考水深面(低于平均海面4 km处的参考面)的地形起伏高度进行表示。由于考虑非线性项与只考虑线性项的反演结果差异远小于海底地形的量级，因此考虑非线性项与只考虑线性项的反演结果图没有明显区别，文中只给出取线性项的海底地形反演图，具体非线性项的影响在表1中以数据形式体现。

图13 取线性项的海底地形反演结果Fig.13 Predicted bathymetry with first order

反演的精度可由反演水深结果与未参与计算的船测控制点水深进行比对，表1对考虑一阶线性项和多阶非线性项的反演数据精度进行统计。

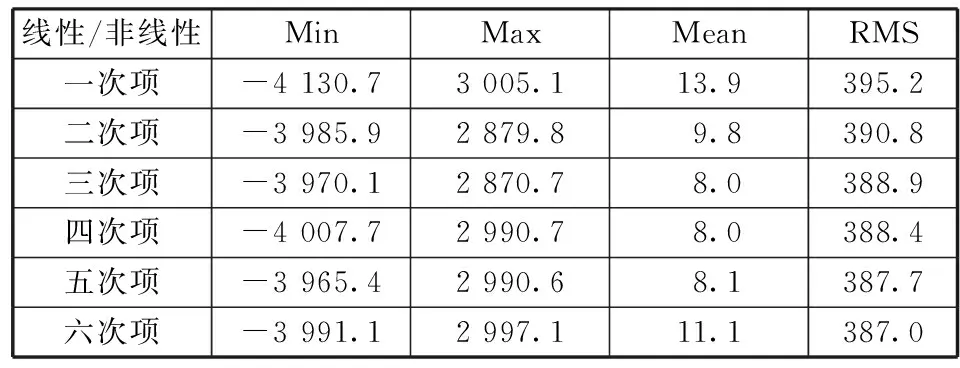
表1 海底地形反演数据统计

将反演得到的海底地形与船测数据进行相关性检验可得数据如图14所示。

图14 反演海底地形与船测数据的相关性Fig.14 Coherence between predicted bathymetry and shipboard bathymetry

根据表1及图14可看出，在20～200 km的波段范围内，重力异常与海底地形以线性关系为主，叠加非线性二次项和三次项将反演精度的平均值量级提升至米级，反演得到的海底地形与船测数据的相关性也有较大提高，高于三次项的部分对反演的结果没有明显的作用，同时由于控制点数据量有限，更高阶的关系系数并不能准确地获得，从而导致从五阶之后阶数增大反演结果却并不理想。

5 结束语

本文详细研究并推导了由卫星测高数据反演海底地形的原理及方法，基于此方法，利用卫星测高重力异常数据和船测水深数据对北太平洋10°×10°的区域进行海底地形反演。数据及分析结果表明：该方法可以有效地反演海底地形，且海底地形与重力异常数据在20～200 km波段内主要呈现线性关系，非线性二次项和三次项对反演精度的提升具有一定的作用，高于三次项的部分对反演的结果没有明显的作用。由于波长小于20 km和波长大于200 km海底地形起伏引起重力异常的物理机理非常复杂，且重力异常在向下延拓时会出现解不唯一且不稳定的问题，由此产生的低于20 km和高于200 km波段的重力异常数据不能准确地与船测水深数据建立关系，也是导致最终海底地形反演精度不高的原因之一。因此，未来对全波段重力异常与水深关系的研究将具有非常重要的意义。

References)

[1]Walter H F Smith, David T Sandwell. Bathymetry prediction from dense satellite altimetry and sparse shipboard bathymetry[J]. Journal of Geophysical Research, 1994, 99(B11): 21803-21824

[2]T H Bell. Statistical features of sea-floor topography[J]. Deep Sea Research, 1975, 22: 883-892

[3]D C McAdoo, K M Marks. Gravity fields from Geosat and ERS-1 satellite altimetry for geodynamic applications[J]. Eos Trans, 1992(74): 133

[4]D T Sandwell, Walter H F Smith. Global marine gravity from ERS-1, Geosat and Seasat reveals new tectonic fabric[J]. Eos Trans,1992, AGU(73):133

[5]G A Neumann, D W Forsyth, D T Sandwell. Comparison of marine gravity from shipboard and high-density satellite altimetry along the mid-Atlantic ridge, 30.5°-35.5°S[J]. Geophysical Research Letters, 1993, 20(15): 1639-1642

[6]吕华庆. 物理海洋学基础[M]. 北京：海洋出版社, 2012

LU Huaqing. Fundamental of physical oceanography[M]. Beijing: Ocean Press, 2012 (in Chinese)

[7]T H Dixon. Bathymetric predition from Seasat altimeter data[J]. Journal of Geophysics and Research, 1983, 88: 1563-1571

[8]G Ramillien, A cazenave. global bathymetry derived from altimeter data of the ERS-1 geodetic mission[J]. Journal of Geodynamics, 1997, 23: 129-149

[9]C Hwang. A bathymetric model for the South China Sea from satellite altimetry and depth data[J]. Marine Geodesy, 1999, 22(1): 37-51

[10]黄谟涛,翟国君，欧阳永忠, 等. 卫星测高资料在反演海底地形中的应用[J]. 海洋测绘, 2002, 22(1): 3-7

Huang Motao, Zhai Guojun, Ouyang Yongzhong, et al. Applications of satellite altimetry data in bathymetry prediction[J]. Hydrographic Surveying and Charting, 2002, 22(1): 3-7 (in Chinese)

[11]C Hwang. Inverse Vening-Meinesz formula and deflection-geoid formula: applications to the predictions of gravity and geoid over the South China Sea[J]. Journal of Geodesy, 1998, 72(5): 304-312

[12]Hu Minzhang, Li Jiancheng, Li Hui, et al. Bathymetry predicted from vertical gravity gradient anomalies and ship soundings[J]. Geodesy and Geodynamics, 2014, 5(1): 41-46

[13]欧阳明达,孙中苗,翟振和, 等.采用重力异常的导纳理论推估海底地形[J]. 测绘学报, 2015, 44(10): 1092-1099

Ouyang Mingda, Sun Zhongmiao, Zhai Zhenhe, et al. Bathymetry prediction based on the admittance theory of gravity anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1092-1099 (in Chinese)

(编辑：张小琳)

Bathymetry Prediction and Analysis Based on Satellite Altimetry Data

SUI Xiaohong1,2ZHANG Running3WAN Xiaoyun2LI Yang1

(1 DFH Satellite Co., Ltd., Beijing 100094, China) (2 Qian Xuesen Laboratory of Space Technology, Beijing 100094, China) (3 Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)

Both of the resolution and accuracy of bathymetry model is far from the model of the earth land and geoid, because of observing difficulty. The traditional measurement of the bathymetry is using shipboard sounding technique, which has the limitations of low efficiency, sparse and nonuniform covering. In this paper, bathymetry prediction method based on satellite altimetry data is presented. An 1′×1′ bathymetry model of a region in north Pacific is predicted through simulation in this paper, and the nonlinear relationship between satellite altimetry data and bathymetry data is analyzed. The results show that, it is feasible to use this method predicting bathymetry. The relationship between satellite altimetry gravity anomalies and bathymetry is mainly linear in certain wavelength; adding the second and third order nonlinear terms will improve the accuracy of the inversion, however the higher order terms have little effect.

bathymetry; satellite altimetry; gravity anomalies; shipboard sounding technique

2017-02-01；

2017-05-26

国家自然科学基金(41404019，41674026)，中国科学院太空应用重点实验室开放基金(CSU-WX-A-KJ-2016-044)

眭晓虹，女，博士研究生，研究方向为卫星测高总体设计及应用。Email：yuanyuansui@hotmail.com。

P228

A

10.3969/j.issn.1673-8748.2017.03.020