牛顿插值法在凸轮修正设计中的应用

班涛++邓利华

摘 要：文章利用牛顿插值法，提出了一种简单实用的凸轮工作轮廓线的修正方法。首先对要进行修正的的曲线附近的一些离散点的数据进行分析处理，确定插值多项式的阶次以满足高精度和低运算量的要求。然后利用Matlab编程计算出插值点的值，并进行误差分析，实现对凸轮的局部工作廓线进行修正。

关键词：凸轮轮廓线；牛顿插值法；修正

中图分类号：TH132.47 文献标志码：A 文章编号：2095-2945（2017）20-0094-02

1 问题的提出及分析

高速包装机械中凸轮工作廓线的设计多采用解析法，这样既保证了凸轮的运动特性，又便于对凸轮机构进行运动学和动力学分析，因此在不同工况下，凸轮设计的解析方程式往往是不同的。这样虽然能保证凸轮的精度，但同时也提高了凸轮在实际使用中的修正难度，因为只有建立新的解析方程式才能对凸轮进行修正，尤其是只需对凸轮局部曲线进行修正时，也要建立相应的解析方程，这样就增大了曲线修正的工作量，降低了工作效率[1]。本文基于提高工作效率和减小修正量的考虑，结合牛顿插值法，提出了一种简单实用的凸轮工作廓线的修正设计方法，这种方法不必对原有的解析方程进行修改计算，只需通过对拟进行修正的曲线附近的一些离散点的数据进行处理，就能对现有凸轮工作廓线进行修正，特别适合凸轮曲线在实际使用中的局部修正设计[2]。已知两个变量X，Y之间的一个离散的函数关系式y（i）=f（xi），i=0，1，…n，即给出一部分数据如表1，找到一个与原函数近似的简单的多项式函数，使其在一部分离散点xi，x0，x1，…，xn的值分别与f（xi），f（x0），f（x1）……f（xn）相等。根据以上要求，可以使用插值多项式来逼近原解析函数。

Lagrange插值公式结构紧凑，便于理论分析，利用插值基函数也容易得到插值多项式。缺点是当插值节点增加，或其位置变化时，全部插值基函数均要随之变化，从而整个插值公式的结构也发生变化，这在实际计算中是非常不利的。Newton插值多项式则可以克服上述缺点，可以灵活地增加插值节点进行递推计算。该公式形式对称，结构紧凑，比Lagrange插值法计算量省，且便于程序设计。

2 模型的建立

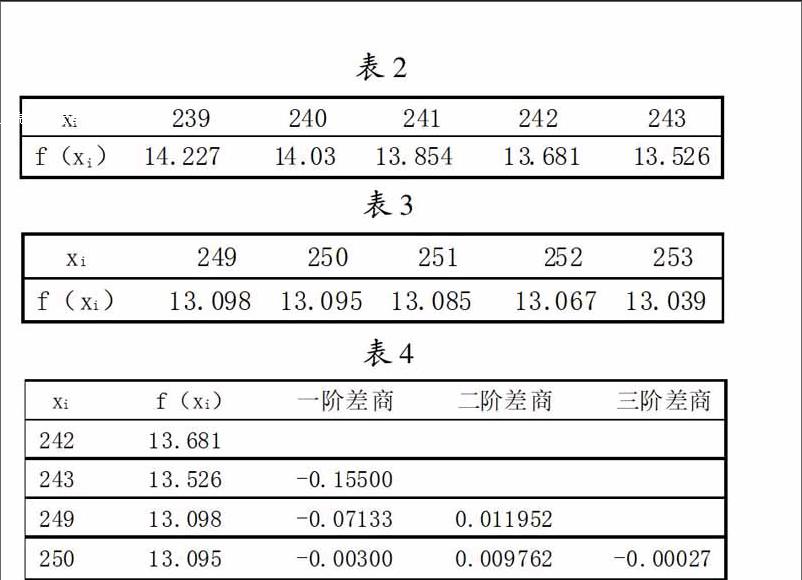
高速包装机上有一凸轮，其工作廓线共有分A、B、C三段，在实际的使用中发现A段和C段的行程符合设计要求，而B段的行程须进行修正设计。已知凸轮A段曲线数据，如表2所示。已知凸轮C段曲线数据，如表3所示。一般来说，使用的已测数据点越多，可获得的信息量越大，对未知点的估计越精确。在牛顿插值算法中，使用已测数据点越多，会导致插值多项式的次数过高，出现龙格现象，曲线也会有较多折点。而凸轮的工作多为翻转，需要其工作廓线有很好的圆滑性。由于距离插值点越近的数据对插值点数值的精度影响越大，本文使用xi=242，243，249，250这4个点的数据，根据牛顿插值的定义做差商表，如图表4所示。

由差商表可知，二阶差商的值已接近常数，故牛顿插值多项式近似为二阶即可满足精度要求。为保证其圆滑性，本文采用三次牛顿插值多项式来求B段xi=244，245...248的修正值。

3 算法实现及结果分析

3.1 Matlab程序代码

function f=Newton（x，y，P）

syms t；

n=length（x）； m=length（y）；

if m～=n

error（'样本数据中x与y的对应个数不匹配'）；

return

end

A=zeros（n）； A（：，1）=y；

for j=2：n

for i=1：（n-j+1）

A（i，j）=（A（i+1，j-1）-A（i，j-1））/（x（i+j-1）-x（i））；

end

end

A

f=A（1，1）；

for j=2：n

T=1；

for i=1：j-1

T=T*（t-x（i））；

end

f=f+A（1，j）*T；

end

f=vpa（f，6）；

f=simplify（f）

f=subs（f，'t'，P）

plot（x，y，'*'，P，f）；

保存為Newton.m文件。

3.2 计算结果

3.3 结果分析

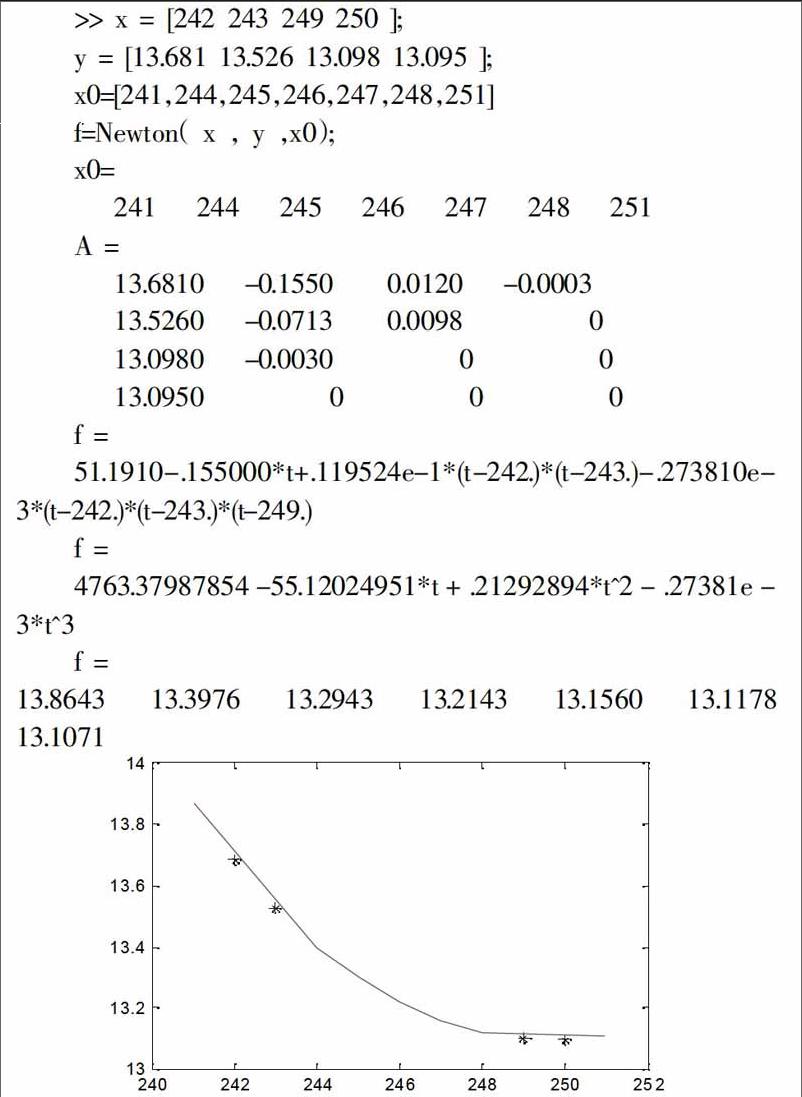
观察上述插值图像，直观上可以满足凸轮工作廓线的圆滑度。具体的数值精度，可以通过量化计算得到。在上述程序中，对x0=241，244，245，246，247，248，251的值均作了插值处理。其中x0=244，245，246，247，248 对应于所要求的进行修正处理的B段曲线的数值点；而计算x0=241，251的值是为了与已知的数据点对比，从而检验牛顿插值计算的精度。可以看出，相对误差都控制在5%以内，属于较好的插值结果。又由于用来检验精度的两个点均为插值数据的外点，误差比内点大得多，故在B段曲线上的点的数据精度应该更高，插值效果更好。

由上述分析可知，B段曲线上插值点的数据比较精确，结果见表6。

4 结束语

用牛顿插值法对凸轮轮廓进行修正设计是一种简单、实用的方法。其优点为：这种方法借助凸轮上一些离散的点的数值就能对凸轮曲线进行修正设计，无需确切知道轮廓线的具体函数表达式及其修正曲线函数，大大节省了计算量；此外掌握的数据越多，进行插值运算时可获得的信息量越大，所得结果的误差也就越小。

参考文献：

[1]贺炜，曹巨江，杨芙莲，等.我国凸轮机构研究的回顾与展望[J].机械工程学报，2005，4（6）：1-6.

[2]邵世权，尚久浩，曹西京.样条函数在凸轮曲线设计中的应用[J].机械科学与技术，2003：135-136.

[3]李庆扬，王能超，易大义.数值分析[M].华中科技大学出版社，2011.