管材壁厚对双直径圆管吸能元件成形与自由翻转的影响

王陶+雷君相+彭彦君+高文静+郭丰伟

摘要： 利用ABAQUS 6.14软件模拟了在不同壁厚下，材料为20钢双直径圆管吸能元件的液压胀形、折叠和自由翻转的过程.并分析了不同壁厚下液压胀形与折叠后的壁厚分布，准静态压缩翻转变形模式以及准静态压缩时翻转力与翻转半径与推导公式之间的关系.结果表明：壁厚减薄程度与管材初始壁厚大小有关；20钢双直径圆管成形后发生轴向压缩时其自由翻转的模式多为内管外翻；推导的翻转力与翻转半径理论公式与实际测得翻转力与翻转半径的结果比较吻合.

关键词： 液压胀形与折叠； 双直径圆管； 翻转力； 翻转半径

中图分类号： TG 386文献标志码： A

Influence of Tube Thickness on the Forming and Free

Inversion of Energy Absorption of Double Diameter Tube

WANG Tao，LEI Junxiang，PENG Yanjun，GAO Wenjing，GUO Fengwei

（School of Materials Science & Engineering， University of Shanghai for

Science and Technology， Shanghai 200093， China）

Abstract： Using ABAQUS 6.14 software to simulate the process of hydraulic forming and folding and free inversion of the original 20 steel double diameter tube with different thickness.The relationship between the thickness distribution of the hydraulic forming and folding，the mode of quasistatic compression deformation and the relationship between the inversion force and the inversion radius of the quasistatic compression and the formula are analyzed.The results show that the tube thickness reduction is related to the degree of initial tube thickness.The mode of selfreversal in the axial compression of 20pipe doublediameter pipe is mostly inner tube valgus.The theoretical formula of the reversal force and the turning radius is consistent with the actual measured turning force and the turning radius.

Keywords： hydraulic forming and folding； double diameter tube； inversion force； inversion radius

近年來，随着公共安全的保护得到越来越多的关注，人们加强了关于结构耐撞性和能量吸收装置的研究[1-2].双直径圆管作为一种有效吸能元件，能够实现载荷最为稳定的目的[3]，因而国内外对其研究也越来越多[4].

利用内高压成形技术[5]，制备出合格的双直径圆管吸能元件.双直径圆管自由翻卷能量吸收结构载荷恒定平稳，成为材料和结构的能量吸收中最理想的能量吸收结构[6-7].在对双直径圆管施加准静态载荷时，在圆角变形区自由翻转时的3种主要有效变形模式：双直径圆管内管外翻、双直径圆管外管内翻和双直径圆管内管外翻与外管内翻复合[8-9].翻转力随着轴向位移的不断增加而增大，逐渐趋向于稳定[10].

本文通过对双直径圆管吸能元件的结构设计，模拟20钢管材在不同壁厚下液压胀形与折叠过程，分析影响管材壁厚减薄与初始壁厚的关系.不同壁厚下，模拟20钢双直径圆管的准静态压缩过程.对比分析各自载荷位移曲线及其自由翻转模式.最后对准静态压缩时翻转力、翻转半径与推导公式之间的关系进行分析.

1有限元模拟

第3期王陶，等：管材壁厚对双直径圆管吸能元件成形与自由翻转的影响有 色 金 属 材 料 与 工 程2017年 第38卷1.1成形过程建模

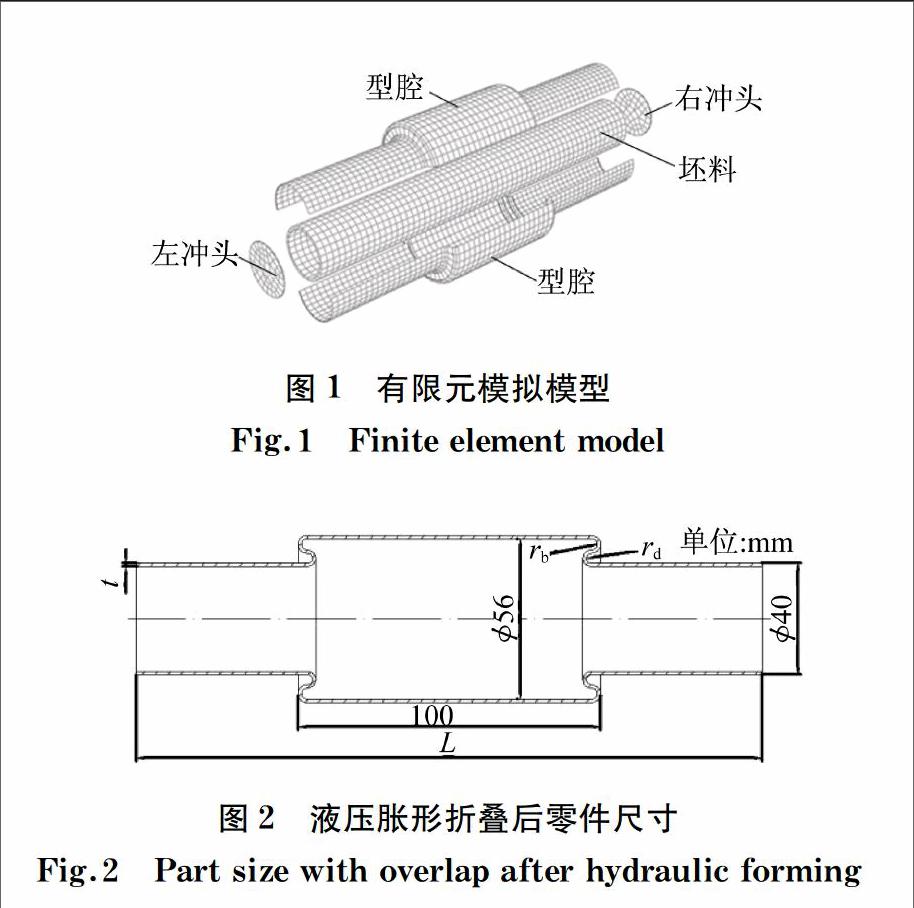
在ABAQUS 6.14软件上建立三维有限元，模拟模型见图1，冲头和模具型腔几何形状为三维壳体，类型为刚体，管坯为三维变形体.管坯划分采用六面体（Hex）单元，结构化网格划分技术.为了观察圆角处的变形，将管坯划分为3层.冲头和模具型腔为刚体，不需要划分网格.管坯和模具型腔之间摩擦接触，摩擦因数为0.1；管坯与冲头之间为无摩擦接触.利用ABAQUS 6.14软件分别对壁厚t为1.2，1.4，1.6和1.8 mm的20无缝钢管的双直径圆管进行模拟液压胀形与折叠过程.成形后的双直径圆管零件需要满足壁厚减薄率小、变形区足长以及成形区壁厚分布均匀的条件，方能称作合格的双直径圆管零件，见图2.双直径圆管吸能元件液压胀形与折叠在一副模具中完成且能一次成形出两个管件.材料参数见表1.

1.2液压胀形与折叠和自由翻转过程模拟

根据图3中液压加载路径以及成形区间图对壁厚t为1.2，1.4，1.6和1.8 mm的20无缝钢管的双直径圆管进行模拟液压胀形与折叠过程.对成形后合格的双直径圆管，分别模拟不同壁厚下的准静态压缩过程.

2模拟结果分析

2.1成形零件壁厚分布比较

管材在液压胀形与折叠过程中壁厚的减薄，对双直径圆管的自由翻转过程影响较大.最大减薄率是判断该零件成形是否合格的重要标准[11].最大减薄率：

ε=δ0-δδ0（1）

式中：δ0为管材初始壁厚；δ为成形后最小壁厚.

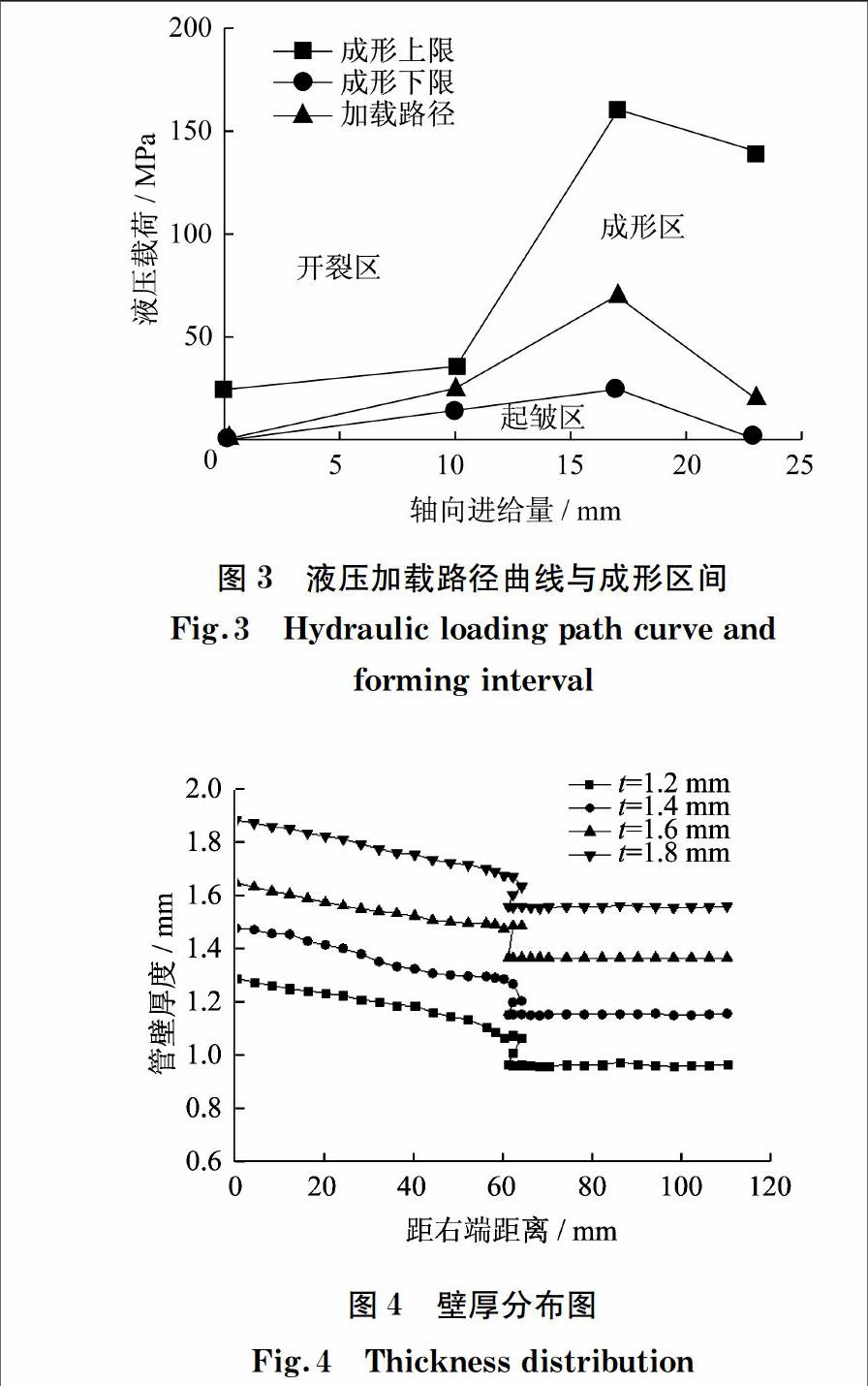
利用ABAQUS 6.14软件的后处理模块，模拟不同壁厚下管材液压胀形与折叠成形后的零件壁厚分布，如图4所示.从图4中可以看出，最大壁厚减薄处均发生在外翻圆角“S”型过渡区处.4种不同壁厚下最大增厚处在管材两端，出现的原因是冲头在轴向进给的时候，兩端受到挤压造成镦粗所致.初始壁厚为1.8 mm的双直径圆管最大减薄率为13.48%，初始壁厚为1.2 mm的双直径圆管最大减薄率为19.88%；初始壁厚为1.4 mm与1.6 mm的双直径圆管最大减薄率初始壁厚为1.2～1.8 mm.从整体来看，4种不同初始壁厚管材的壁厚减薄的变化相对比较均匀，满足成形质量要求.

影响壁厚减薄的因素有很多，除了与管材自身的材料力学性能有关，还与管材与模具之间的摩擦、模具圆角半径以及液压胀形与折叠过程中材料的补充速度有关.本次试验中，模具的圆角半径对壁厚的模拟过程的影响较大.模具圆角半径的尺寸直接影响管材在液压胀形与折叠过程中的材料的流动性，进而影响壁厚的减薄率以及壁厚的均匀度，同时合适的圆角半径能够减小加工硬化带来的不利影响.此次模拟过程中，模具圆角半径为3 mm，通过合理控制液压力与轴向进给量来控制材料的补充速度，可以控制双直径圆管在成形过程中避免变形区出现起皱、屈曲和破裂的失效现象，进而控制壁厚减薄率，管壁厚更为均匀，提高成形合格率.

2.2自由翻转模式与翻转载荷模拟结果分析

液压胀形与折叠后，对4种不同壁厚的双直径圆管进行准静态压缩变形模拟，压缩变形的翻转载荷位移曲线如图5所示.

从图5中可以看出，4种不同初始壁厚的双直径圆管在发生压缩变形时，4种双直径圆管均能达到载荷稳定阶段.初始壁厚为1.8 mm的双直径圆管自由翻转载荷上升幅度较快，载荷相对平稳，承受的翻转载荷相对较大.初始壁厚为1.2 mm的双直径圆管自由翻转载荷在趋于平稳过程中存在一定的波动，达到载荷稳定时的行程相对较长.初始壁厚为1.4 mm与1.6 mm的双直径圆管自由翻转载荷状态介于初始壁厚1.2～1.8 mm.

影响翻转载荷的稳定因素有很多，除了材料的性能，还与成形后双直径圆管内外管的壁厚有关.由于内外管壁厚直接影响双直径圆管轴向压缩变形模式，进而影响翻转载荷的平稳.初始壁厚为1.8 mm的双直径圆管外管减薄相对较少，受材料加工硬化的影响较大，外管不容易变形，屈服应力增大，内管向外翻转趋势比较大，故翻转模式以内管外翻为主，载荷较为稳定.初始壁厚为1.2 mm的双直径圆管外管壁厚相对较大，外管有向内翻转的趋势，但加工硬化的影响仍存在，故在到达载荷稳定阶段会出现一段波动，翻转模式会出现小段内管外翻的阶段，但仍然以内管外翻为主要翻转模式.初始壁厚为1.4 mm与1.6 mm的双直径圆管自由翻转的模式也以内管外翻为主，承受载荷稳定.

由文献[12]推导的双直径圆管自由翻转吸能元件发生内管外翻时的翻转力公式以及翻转半径公式[12]为：

P=πdtβS—ln1+2rdd+tt+2rdKd（2）

r=d2KdKdtd+34td2-t2d（3）

式中：β与材料的本构关系有关，各向异性时，β=2（1+rd）1+2rd；S—为材料的幂指强化系数；d为内管外径；Kd为内管外翻系数，Kd=ln1+4rdd.

结合双直径圆管的尺寸，得出4种壁厚双直径圆管准静态压缩下的模拟结果和理论结果，如表2所示.

初始壁厚/mm翻转形式稳定翻转力/kN理论翻转力/kN外翻圆角半径/mm理论圆角半径/mm1.2内管外翻22.3421.151.281.341.4内管外翻25.1424.901.361.451.6内管外翻31.4729.221.491.581.8内管外翻37.1236.871.621.66

同时将上述结果与Guist & Marble提出的翻转力与翻转半径公式[13-14]和Reddy提出的翻转力与翻转半径公式[15-16]所得出的结果进行对比，如图6所示.

从图6中可以看出，文献[12]推导的双直径圆管自由翻转吸能元件发生内管外翻时的翻转力公式及翻转半径公式得出的结果，较Guist & Marble和Reddy提出的翻转力与翻转半径公式所得出的结果更接近模拟值.说明该公式使用在双直径圆管发生内管外翻时预测翻转力与翻转半径较为准确.

3试验分析

对成形后的双直径圆管在Zwick试验机上进行轴向压缩试验.成形后的双直径圆管零件和准静态压缩后剖视的结果如图7所示.

准静态压缩后载荷位移曲线如图8所示.

准静态压缩试验中测得的翻转力和翻转半径的大小与理论计算的结果对比如图9所示.

从图7中可以看出，在准静态压缩试验过程中，双直径圆管在发生自由翻转时，4种不同壁厚的双直径圆管翻转模式并非刚开始就发生内管外翻，而是开始翻转阶段发生了小部分的外管内翻，随后发生内管外翻，总体趋势以内管外翻为主.出现此类情况的原因，可能与管材液压胀形成形后内外壁的壁厚以及成形过程中加工硬化有关，导致不能以单一的翻转模式进行.

从图8中的准静态压缩试验结果和模拟结果可以看出，载荷位移曲线的变化趋势大致相同，试验中承受的载荷值比模拟结果略大.但整体来看，模拟结果与试验结果基本吻合.

从图9中可明显看出，实际测得的翻转力比理论值大，实际测得的翻转半径比理论值小.但是较Guist & Marble提出的翻转力和翻转半径公式与Reddy提出的翻转力与翻转半径公式得出的结果更接近实际值.

4结论

（1） 4种不同壁厚的管材均在合适的加载路径下成形出合格的双直径圆管吸能元件，不同壁厚的管材的减薄率各不相同，且与壁厚有关.初始壁厚为1.8 mm的双直径圆管的最大减薄率为13.14%.

（2） 相同条件下，4种不同壁厚的20钢双直径圆管在发生自由翻转时均以内管外翻的翻转模式为主，翻转载荷稳定可控，可以用作吸能元件和各种碰撞吸能场合.

（3） 从模拟与试验相结合的角度来看，当双直径圆管發生内管外翻时，由文献[12]推导的双直径圆管吸能元件翻转力公式以及翻转半径公式得出的结果更为精确可靠.

参考文献：

[1]殷之平，李玉龙，黄其青.薄壁圆筒结构耐撞性优化设计[J].机械科学与技术，2010，29（2）：220-224.

[2]ZHANG X，HU H H.Energy absorption of longitudinally grooved square tubes under axial compression[J].ThinWalled Structures，2009，47（12）：1469-1477.

[3]余同希，卢国兴.材料与结构的能量吸收[M].华云龙，译.北京：化学工业出版社，2006.

[4]张立玲，高峰，杜发荣.不等厚拼焊管轴向压缩变形的数值模拟研究[J].塑性工程学报，2006，13（4）：6-9，19.

[5]ALHASSANI S T S，JOHNSON W，LOWE W T.Characteristics of inversion tubes under axial loading[J].Journal of Mechanical Engineering Science，1972，14（6）：370-381.

[6]苑世剑，王小松.内高压成形技术研究与应用新进展[J].塑性工程学报，2008，15（2）：22-30.

[7]汪奇超，雷君相，骆协海.铝合金防碰撞吸能管液压成形加载路径研究[J].锻压技术，2011，36（6）：55-58.

[8]邱信明，贺良鸿.圆管准静态翻转的三维模型分析[J].失效分析与预防，2011，6（1）：1-7.

[9]刘钢，董哲，苑世剑.加载路径对TAl5板材热拉深气胀成形筒形件减薄率的影响[C]∥第十二届全国塑性工程学术年会暨第四届全球华人塑性加工技术研讨会.重庆：中国机械工程学会，2011.

[10]邓天根，雷君相.变径管自由翻转变形的趋向性研究[J].锻压技术，2014，39（2）：144-149，153.

[11]岳永保，杨合，詹梅，等.薄壁管小弯曲半径数控弯曲壁厚减薄实验研究[J].锻压技术，2007，32（5）：58-62.

[12]徐龙江，雷君相，高贵杰.变径管与薄壁圆管轴向压缩过程研究[J].机械工程与自动化，2015（3）：137-138，144.

[13]GUIST L R，MARBLE D P.Prediction of the inversion load of a circular tube[R].Washington，D.C.：NASA，1966.

[14]TOMESANI L.Analysis of a tensiondriven outsidein tube inversion[J].Journal of Materials Processing Technology，1997，64（1/3）：379-386.

[15]REDDY T Y.Tube inversionan experiment in plasticity[J].International Journal Mechanical Engineering Education，1989，17（4）：277-291.

[16]REDDY T Y.Guist and Marble revisitedon the natural knuckle radius in tube inversion[J].International Journal of Mechanical Sciences，1992，34（10）：761-768.有色金属材料与工程第38卷第3期NONFERROUS METAL MATERIALS AND ENGINEERINGVol.38No.32017