森林工程教学课堂融入高等数学知识的研究

胡志栋++董喜斌

摘要 针对学生缺少足够的高等数学知识解决工程实践中实际问题的现状，为了在森林工程课堂教学中将高等数学知识与工程实践更好地结合，基于实际的研究工作，对用于解决常微分方程的显式欧拉法、隐式欧拉法、改进欧拉法、龙格库塔法和ODE45方法进行了介绍和对比研究。结果表明，这些方法在解决常微分方程的数值解上是一致的，而且相互之间的误差很小。介绍了解决偏微分方程的PDE 方法。在建模的过程中用到了有限元方法，在方程的列写过程中用到了矩阵方法，通过理论分析可以看出，矩阵表示的是实际问题与空间、时间的关系，因而可以从直观的角度去理解抽象的矩阵知识。这些方法可以很好地帮助森林工程领域的学生在今后的工作中建立数学模型并加以分析，从而加强解决实际工程问题的能力，也为森林工程课题今后的教学提供一定的参考。

关键词 高等数学；森林工程；教学课堂；常微分方程（ODE）；偏微分方程（PDE）；矩阵

中图分类号 G542 文献标识码 A 文章编号 1007-5739（2017）11-0272-04

1 研究背景概述

纵观世界数学发展史，17—19世纪的英国、德国、法国等欧洲大国都是数学强国。英国的牛顿提出了微积分理论，不仅在数学领域引发一场革命[1]，同时也大量应用于许多物理问题的研究。法国一直拥有深厚的数学文化发展历史，而德国的哥廷根于20世纪初成为世界数学的中心[2]。俄罗斯在数学领域的发展从19世纪开始，至苏联时期成为世界数学强国之一。特别是苏联于1958年成功发射了第一颗人造地球卫星，也象征着苏联在与此相关的数学领域处于世界领先地位。此外，苏联重视基础科学教育，也是其在基础科学研究中具有雄厚实力的一个重要原因。第二次世界大战前美国在数学上远落后于欧洲，但如今也已成为数学超级大国。一方面由于大批犹太裔数学家被迫移居美国，增强了美国的数学实力[3]；另一方面在苏联发射第一颗人造地球卫星后，美国加强了对数学研究和数学教育的投入，使其迅速成为一个数学强国。

学界普遍认为下一次科技革命将以人类3种新的“生存形式”为重要标志，即网络人（生活在网络空间的虚拟人）、仿生人（高仿真智能人）和再生人（具有自然人特征的“复制人”）。并预计这次科技革命将在2020—2050年到来。数学对整个社会经济的发展起着至关重要的作用[4-6]，在前几次科技革命中都起到了先导与支柱的作用，因而有理由相信数学必将成为下一次科技革命重要的推动力之一[7]。由此可见数学在科技发展中的重要地位[8]，本文对于将高等数学知识应用到森林工程教学课堂进行研究，以期推动数学在教育领域的综合应用。

为了更好地说明如何将高等数学知识应用到森林工程教学课堂，文中采用了基于气穴气泡研究的一个实例。在过去的几个世纪中，气穴问题在森林工程领域一直被认为是流体机械气蚀问题的主要起因之一。大量的试验和数值分析工作都是围绕企图找出气蚀问题的产生机理展开的。Rayleigh[9] 最先开始这方面的工作，其研究认为圆形气泡溃破时产生的局部高压，即气穴是产生气蚀现象的原因。式（1）为R-ayleigh推导得到的经典气穴气泡动力学方程。

r■+■■2=■（1）

式（1）中：r为气泡半径（m）；PB为气泡内的压力（Pa）；P∞为外界无穷远处的压力（Pa）； ρ为流体的密度（kg/m3）；t为时间（s）。

2 研究方法

2.1 量纲分析方法

国际单位组织定义了7个最基本的单位，其他的单位都可以由这7个基本单位导出。这7个基本单位分别为长度，米（m）；质量，千克（kg）；时间，秒（s）；电流，安培（A）；热力学温度，开尔文（K）；发光强度，坎德拉（cd）；物质的量，摩尔 （mol）。长度、质量和时间这3个基本单位是森林工程课堂中常用的单位。

量纲分析法又称为因次分析法，是一种数学分析方法，其可以正确地分析各变量之间的关系，简化试验和成果整理，所以量纲分析是分析流体运动的有力工具。通过量纲分析可以检查反映物理現象规律的方程在计量方面是否正确，甚至可提供寻找物理现象某些规律的线索。

应用量纲分析法，式（1）可以写成：

m■+■■■=■∝■■（2）

通过这种分析方法，推导过程的准确性可以很容易得到保证，而且方程的特性和实质也很容易发现。

2.2 ODE求解方法

在数学领域中，只包含一个独立变量及其导数的单个或多个微分方程被称为常微分方程（ODEs）。常微分方程广泛应用于数学、工程和科学等领域。在数学中“变化”是用导数和微分来描述的。种类繁多的导数、微分及函数通过方程联系在一起，用来刻画各种动态变化的现象、进化或演变过程。

如果式（1）中的压差为定值，那么它属于一个ODE问题，然后对比研究显式欧拉法（Forward Euler′s method）、隐式欧拉法（Backward Euler′s method）、改进欧拉法（Modified Euler′s method）、ODE45方法和龙格库塔法（Runge-Kutta method）在分析ODE问题上的应用[10]。

显式欧拉法表达式：

ri+1=ri+h×f（ti，ri）（3）

隐式欧拉法表达式：

ri+1=ri+h×f（ti+1，ri+1）（4）

改进欧拉法表达式：

ri+1=ri+■×[f（ti+1，ri+1）+f（ti，ri）]（5）

4阶龙格库塔法表达式：

ri+1=ri+■×[K1+2K2+2K3+K4]（6）

式（6）中参数的计算如下：

K1=fti，riK2=fti+■，ri+■K1K3=fti+■，ri+■K2K4=fti+h，ri+hK3（7）

式（3）～（7）中：h为步长。

ODE45方法是MATLAB程序软件包内植的一条命令程序。

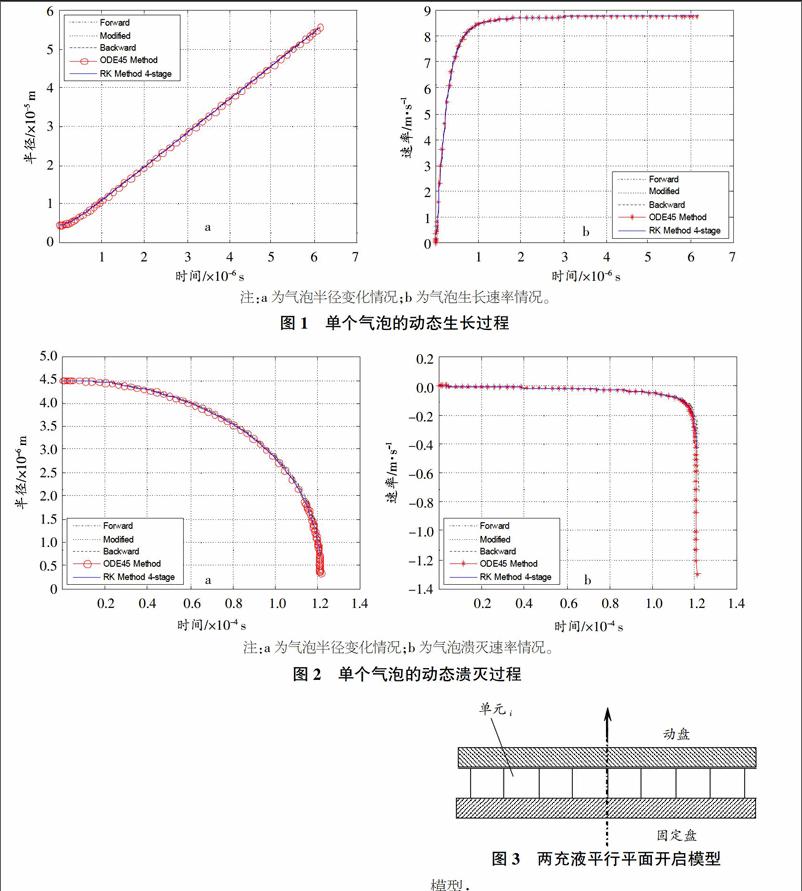
首先应用上述方法分析单个气泡的动态生长过程，包括气泡半径变化情况和生长速率情况（图1）。

再應用上述方法分析单个气泡的动态溃灭过程，包括气泡半径变化情况和溃灭速率情况（图2）。

通过对比可以看出，这5种方法在解决单个气泡的动态问题上是统一的，它们之间的误差也很小。

2.3 矩阵方法

矩阵是数学中最重要的基本概念之一，是代数学的一个主要研究对象，也是数学研究及应用的一个重要工具。在数学中，矩阵是一个按照长方阵列排列的数、符号或表达式组成的集合。在不知道矩阵如何得来的情况下分析矩阵是很抽象的。为了更好地使学生理解矩阵的应用，通过两充液平行平面的动态开启过程实例来加以解释。

在一定的初始间隙值下，建立两充液平行平面的动态开启模型，然后通过理论分析可以得到开启过程中压力分布的变化情况（图3）。

首先针对没有气穴气泡的情况，为了分析压力分布的变化情况，针对第i个单元，运用间隙流动的理论公式和有限元方法得到理论公式，最后用矩阵的方法得到整个问题域的数学模型：

■×■=■（8）

式（8）中：h（t）为开启高度函数；η为液体的动力黏度（Pa·s）。

1 0 0 L 02 -3 1 O 0 1 -2 1 O M 0 1 -2 1 M O O O O 0 L 0 1 -2 10 L 0 1 -1 p■p■p■p■Mp■p■=a1p0/a1h′（t）h′（t）h′（t）Mh′（t）h（t）（9）

式（9）用向量表示可以简写为：

■■=a■■（10）

式（10）中：a■=■，■=1 0 0 L 02 -3 1 O0 1 -2 1 O M 0 1 -2 1M O O O O 0 L 0 1 -2 10 L 0 1 -1，

■=P■P■P■P■MP■P■，■=p■/a■h′（t）h′（t）h′（t）Mh′（t）h（t）。

通过MATLAB编程求解，就可以得到压力分布与空间、时间的关系（图4）。

2.4 PDE求解方法

在数学领域，如果一个微分方程中出现多元函数的偏导数，或者说如果未知函数和几个变量有关，而且方程中出现未知函数对应几个变量的导数，那么这种微分方程就是偏微分方程。

许多问题用一个自变量的函数来描述已不够，不少问题由多个变量的函数来描述。比如，从物理角度来说，物理量有不同的性质，温度、密度等是用数值来描述的，叫做纯量；速度、电场的引力等不仅在数值上有不同，而且还具有方向，这些量叫做向量；物体在一点上的张力状态描述出的量叫做张量。这些量不仅和时间有关系，而且和空间坐标也有联系，这就要用多个变量的函数来表示。

同样地，针对两充液平行平面的动态开启过程，Matlab软件提供了一个求解PDE问题的工具箱“pdepe”。基于pdepd方法的压力分布见图5。在求解的时候，初始条件IC（Initial Condition）和边界条件BC（Boundary Condition）是需要提前确定的[11-13]。

Cx，t，u，■■=x■-m■xmfx，t，u，■

+Sx，t，u，■（11）

令 m=0， x？缀[0，0.012 5]，t？缀[0，0.002] ，fx，t，u，■=■，

Cx，t，u，■=0，Sx，t，u，■=-■■，

IC：p（x，0）=1bar，BC：p（0，t）=1barp（0.012 5，t）=1bar。

通过图4和图5的对比研究可以看出，PDE求解和理论分析的结果是一致的，这为以后的理论分析提供了另外一条途径。

如果将两充液平行平面的开启过程和气穴气泡的动态生长过程结合起来，则可得出理论分析模型，具体如图6所示。

同时考虑流体的黏度，则含有气穴气泡的两充液平行平面动态开启过程可以用式（12）和式（13）来描述。

r■+■■■2+4■=■（12）

1 0 0 … 02 -3 1 …0 1 -2 1 … … 0 1 -2 1… … … … … 0 … 0 1 -2 10 … 0 1 -1p■p■p■p■？噎p■p■=a1p■/a■h′（t）h′（t）h′（t） ？噎h′（t）h（t）-a2■0

r12■1

r22■2

r32■3

？噎

r2N-1■N-1

r2N■N（13）

式（13）用向量表示可以简写为：A

■■=a1■-a2■（14）

式（14）中：a■=■，■=0r12■1r12■1r22■2r32■3？噎r2N-1■N-1r2■■N■N。

在每个单元内的每个气泡的整个生命周期变化情况可以获得（图7）。

3 结论

在2个充液平行平面的动态开启过程中，气穴气泡先是生长而后溃灭。在这个问题研究的基础上，介绍和对比研究了显式欧拉法、隐式欧拉法、改进欧拉法、龙格库塔法和ODE45方法在数值分析ODE问题上的应用。结果表明，这些方法在解决ODE问题上是互相吻合的，在步长足够小的情况下它们之间的误差也非常小[14-16]。

这些方法在MATLAB环境下编程也不复杂，这样就可以结合其他的程序获得复杂问题的数值解。看起来很抽象的矩阵其实它表示的是向量之间在时间、空间上的关系，一旦这些关系确立以后，通过分析就可以得到很直观的解释。另外，还介绍了解决PDE方程的方法。在建立两平行平面的动态开启模型时，使用的是有限元法。

在实际的森林工程实践中，有很多问题需要用微分方程来刻画[17-20]，本研究旨在说明如何将高等数学知识与工程实践更好地结合，在今后的森林工程课堂教学中加强这方面的运用，让学生在今后的工作中有能力做出精确的分析，从而取得更大的发展。

4 参考文献

[1] 刘鸿基，刘刚.数学发展简史及未来趋势简论[J].科技信息，2012（4）：129-130.

[2] 邓明立，张生春.19世纪德国数学发展原因初探[J].自然辩证法研究，2000（8）：45-49.

[3] 赖发孝.浅析高中数学在社会经济发展中的作用[J].经贸实践，2016（18）：36.

[4] 张奠宙.二十世纪数学发展一瞥[J].自然杂志，1982（3）：179-182.

[5] 冷萤征.探讨数学在经济发展中的地位及作用[C]//“决策论坛：企业党建与政工创新工作发展学术研讨会”论文集（下）.中国武汉决策信息研究开发中心、决策与信息杂志社、北京大学经济管理学院，2016：1.

[6] 曹建美.数学在现代经济学及经济发展中的作用[N].山西经济日报，2009-12-14（004）.

[7] 张恭庆.数学与国家实力（上）[J].紫光阁，2014（8）：76-78.

[8] 王汝发.从20世纪数学发展再看数学与科学技术之关系[J].广东工业大学学报（社会科学版），2003（1）：57-60.

[9] RAYLEIGH L.On the Pressure Developed in a Liquid during the Colla-pse of a Spherical Cavity[J].Philosophical Magazine，1917，34：94-98.

[10] E HAIRER，S P NORSETT，G Wanner.Solving Ordinary Differential Equ-ations I-Nonstiff Problems[M].Second Revised Edition.Springer press，1992.

[11] SUN Zhizhong.Numerical solutions for partial differential equations[M].Science Publishing House，2005.

[12] DAVID BLEECKER，GEORGE CSORDAS.Basic Partial Differential Eq-uations[M].International Press of Boston，1997.

[13] ANDREI D，POLYANIN.HANDBOOK OF LINEAR PARTIAL DIFFER-ENTIAL EQUATIONS for ENGINEERS and SCIENTISTS （First Edition）[M].CHAPMAN & HALL/CRC，2002.

[14] 杜世拔.森林经营系统工程数学模型的研究[J].林业资源管理，1982（4）：27-29.

[15] 董斌，陈立平，钱国英.基于遥感的层次分析法和模糊数学模型综合评价森林资源生态适宜性[J].自然资源学报，2011（3）：468-476.

[16] 吴发云，孙涛，王小昆.基于数学形态学的森林资源数据更新技术研究[J].林业资源管理，2009（5）：105-108.

[17] 成子纯，吕勇.森林生物数学的发展与展望[J].中南林业调查规划，1997（2）：47-49.

[18] 張映堂，郭安.云南楚雄州林火分布的数学模型及森林防火期的划分[J].西南林学院学报，1996（2）：100-104.

[19] 刘春玲，路紫.数学方法在森林生态旅游区开发中的具体应用[J].经济地理，2001（1）：118-120.

[20] 胥晓，苏智先，黎云祥，等.嘉陵江流域南充金城山森林群落的模糊数学分析[J].四川师范学院学报（自然科学版），1999（2）：182-189.