基于Opennesh的三维网格简化算法优化

丁文文

摘要：针对二次误差测度算法折叠排序代价计算标准单一导致模型在具有复杂结构的情况下特征难以保持的不足，提出了基于OpenMesh的三维网格简化算法。在二次误差测度的基础上，通过引入折叠点度和折叠边长度作为计算折叠代价的辅助因素，较好地对网格进行了简化。另外通过判断点、边和面是否处于边界来保持边界尽可能不变，以达到视觉特征基本不变的效果。实验结果表明该算法在较好地保持模型视觉特征的情况下可以快速地对模型进行简化。

关键词：半边折叠；顶点度；折叠边长度；网格简化

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2017）17-0200-03

1概述

随着计算机技术的快速发展，虚拟现实技术逐渐步人大众的视线。但是在充分利用虚拟现实技术之前却面临着巨大的挑战。一个主要的因素是虚拟现实中的模型通常非常巨大，这对硬件的要求往往会超过普通用户的承受标准，甚至有些场景即使当今比较先进的硬件也难以流畅地渲染，因此三维模型的简化仍需要继续研究。例如斯坦福大学的数字米开朗琪罗计划中的大卫雕像的三角面片数高达20亿，远远超出了一般显卡的处理能力。实际上早在20世纪七十年代就已经有了关于模型简化的讨论，也就是后来广泛应用的多细节层次（Levels of Detail，LOD）技术。该技术通过简化模型细节来降低场景复杂度，从而保证场景能流畅地进行渲染和加载，尤其适合运用于当今火热发展的虚拟现实技术中。根据简化机制，有学者将常用的简化算法分为顶点聚类（Veriex Clustering）、增量式简化（Incremental Decimation）、采样（Sampling）和自适应细分（Adaptive Subdivision）。Schroeder首先提出了顶点删除的网格模型简化算法，随后基于边折叠、基于三角形删除等方法相继被提出，这些方法的共同点是删除网格模型中对外观影响较小的面片。几何元素删除法（点删除、边折叠、半边折）在模型简化时有较好的复杂度和效果，另外还有CGAL（Computational Geometry Algorithms Library）和OpenMesh等开源库作为支撑。相比边折叠算法，半边折叠不用计算新顶点位置。QEM对全局能量最小化算法进行极大的简化，适合对模型进行快速简化。在此基础上，殷智慧等人通过引入顶点的曲度特征因子以及抑制狭长三角形的生成保持模型的几何特征。熊仕勇等人通过引入二次误差量度、曲率特征、视觉特征度、顶点度以及边长来计算半边折叠代价，有效解决了简化后模型重要几何特征不明显的问题。本文在研究半边折叠算法理论的基础上，对半边折叠算法进行了改进，通过添加顶点度和折叠边长度等因子在尽量保持特征的情况下对模型进行快速简化。

2半边折叠算法

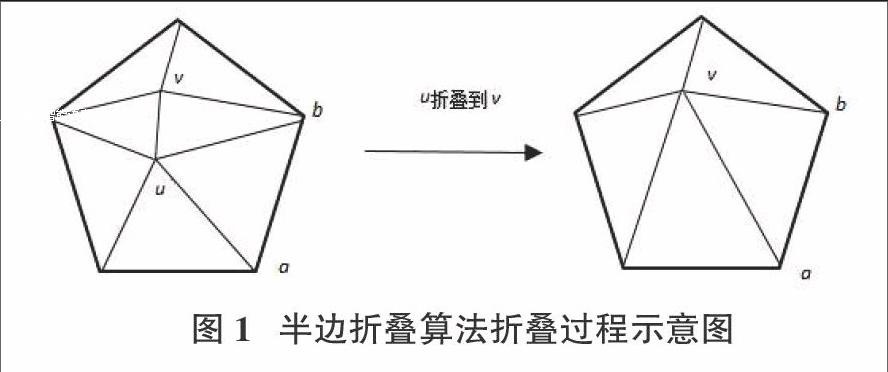
二次误差最早由Garland提出，采用点到平面的距离平方作为误差测度。图1是半边折叠算法折叠过程示意图：

3半边折叠算法改进

基于QEM的半边折叠算法的优点是具有较高的计算速度和较小的内存消耗而且能得到较高质量的网格。在已有的一些简化算法误差测度中，有的速度非常快但简化质量很差，有的速度很慢但简化质量非常好。而这种方法刚好是两类方法之间的一种折中，是一种兼顾了速度和质量的较理想的误差测度。

除了以上的优点之外，基于QEM的半边折叠也有其不足，主要是基于距离平方作为考虑因素过于单一，没有考虑边的长度和度数等因素，可能出现狭长三角形等导致模型视觉特性变化较大的情况。因此本文在QEM的基础上添加顶点的度和折叠边长度作为新的代价因素添加到QEM算法中进行半边折叠。另外考虑点、边和面是否是边界来进一步减少模型视觉特征的丢失，实验结果证明本改进算法有较好的简化效果。

在三维网格开源库中，CGAL功能强大，适用于大型项目。相比之下OpenMesh则短小精悍，更有利于小型工作的开展。OpenMesh底层采用半边数据结构（Half-Edge Data Structure），方便进行点、边和面的遍历。本文将利用OpenMesh提供的基础应用程序接口实现基于QEM的半边折叠简化算法优化。

在计算折叠代价的时候需要考虑顶点的度，该因素可以考量有多少点与该点相连接。其相邻点越多则其重要性越大，应该使其权重加大，折叠优先级降低，从而减少密集点被折叠的次数，以达到更好保持模型视觉特征的目标。在处理过程中，如果有孤立点的存在则会将该点删除。如果该顶点不是孤立点则通过OpenMesh提供的循环器算出顶点度用于后续折叠代价计算。

另一个折叠代价因素是折叠边的长度。在QEM算法中没有考虑到折叠边的长度，可能导致狭长三角形情况的出现，从而使模型产生较大的视觉变化。OpenMesh中点存储为三维浮点坐标，非常方便计算边的距离。本文加入折叠边的长度作为辅助因素，在进行边长度较大的折叠的时候会加大其折叠代价，从而尽量使较长边的折叠优先级降低。

OpenMesh提供了判断点、边和面是否為边界的函数，即is_boundary（）。使用该函数并传人点的指针参数即可判断该点是否为边界点。为了保持模型的视觉特征尽可能不变，应该对边界点的权重进行增加。折叠边界点的代价会变大，从而在边折叠的过程中减少边界点的折叠，保持模型边缘尽少改动。

顶点对（u，v）订的折叠代价计算：

1）根据QEM算法计算其二次误差Q。

21使用OpenMesh提供的循环器计算顶点的度，记为de-gree。

3）根据is_boundary（）函数测试点是否为边界点。如果是边界点则权重加倍，那么折叠代价cost=2*degree*Q，否则cost=degree*Q。

4）计算折叠边长度为len，折叠代价cost=len*cost。

本算法的折叠过程如下：

1）对所有顶点v_i计算Q_i。

2）计算最优折叠目标并对每一对点关联二次误差。

3）将点放入堆中，堆通过最小误差排序。

4）从堆中取得最小误差顶点对（v_i，v_j）；折叠顶点对并移除有关平面；对涉及顶点v_i和v_j的顶点对代价进行更新。

5）判断是否达到预定折叠次数或代价函数阈值，如果未达到则转到步骤4），否则转到步骤6）。

6）折叠结束，保存简化后的模型。

4实验结果

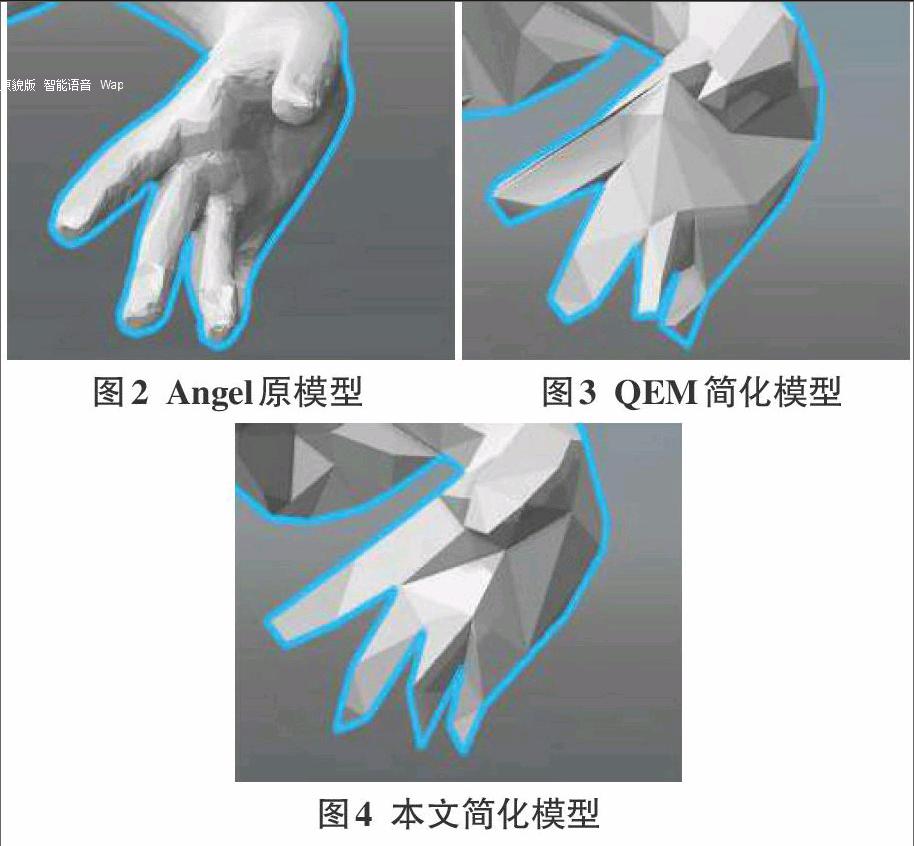
根据以上算法设计思路做了三组对比试验，分别是Angel模型、兔子模型和Predator模型。从图2-4可以看出经过改进之后，中指保持了向内握的特征，而QEM算法优化后的模型则成为了直的，丢失了弯曲的效果：

表1对应该对比实验Angel模型简化的顶点和面片数，从原来的224514个顶点简化到4514个顶点，简化比例为97%左右：

斯坦福大学提供的兔子模型底部是有空洞的，恰好用于对本算法边界点的改进效果进行观察。从图5-7可以看出改进之后的算法洞口附近的点保留得比QEM算法得到的模型点更密集，其轮廓更加细腻：

表2对应该对比实验兔子模型简化的顶点和面片数，从原来的35947个顶点简化到5947个顶点，简化比例为85%左右：

本文另外对Predator模型进行了更大程度的简化，从8-10可以看出QEM简化该圆孔的结果是一个三角形，本文简化同样数量顶点后得到的结果为五边形，对边界特征的保持更好：

表3对应该对比实验Predator模型简化的顶点和面片数，从原来的493383个顶点简化到3383个顶点，简化比例为99.5%左右。

5结束语

本文提出的改进非常适合在边缘区域和顶点连接密集的部位进行简化，可以较好地保持住模型邊缘视觉特征。另外添加了折叠边的长度作为折叠控制因素后可以较好地控制折叠过程中狭长三角形的出现，也是对保持模型视觉特征的多重保证。实验过程中由于需要对折叠顶点对的长度及顶点度进行计算，另外还需要判断边界点等，即使采用速度较快的堆排序仍会多消耗约15%的时间，需要在将来的工作中继续改进。