LCL型并网逆变器的滑模变结构控制策略

李 鹏，王 奔 ，高鲁峰，李 晓，张 锐

(西南交通大学电气工程学院，四川 成都 610031)

LCL型并网逆变器的滑模变结构控制策略

李 鹏，王 奔 ，高鲁峰，李 晓，张 锐

(西南交通大学电气工程学院，四川 成都 610031)

针对三相并网分布式发电系统的运行特点以及LCL滤波器的工作特性，建立三相并网逆变器的数学模型，它在同步旋转dq坐标系下的数学模型, 反映出LCL型并网逆变器是一个强耦合的、非线性的系统。为解决对这个强耦合、非线性系统直接设计控制器的困难，采用逆系统方法，将原系统线性化且解耦, 构造出一个伪线性系统；然后，运用滑模变结构控制，针对构造出的这个伪线性系统，设计该系统的控制策略以实现对LCL型并网逆变器综合控制；最后在Matlab/Simulink 仿真软件中通过建立仿真试验模型进行仿真，仿真的结果验证了所提出的这种控制策略的有效性和较强的鲁棒性。

LCL型滤波器；逆系统；变结构控制；鲁棒性

0 引 言

近年来由可再生能源构成的分布式发电系统蓬勃发展，它们都需要采用并网逆变器与电网相连接[1-2]。由于并网逆变器通常采用PWM调制，从而导致分布式电源输出电流中含有大量高次谐波，影响输出的电能质量，因此必须采取合适的滤波电路。小功率分布式电源通常采用L型滤波器作为并网接口,而大功率分布式电源则采用LCL滤波器。LCL滤波器与L型滤波器相比可以滤除高次谐波，并且成本低，体积小。但是LCL滤波器是一个三阶谐振电路,其谐振对系统的稳定性及并网输出电流波形质量有很大的影响,控制器的设计是决定系统稳定运行以及并网电流质量所必需解决的问题[3-5]。

目前，针对LCL型并网逆变器的控制方法有很多文献进行了分析。文献 [8]采用基于静止坐标变换的比例谐振控制器(PR)，PR控制算法可以实现无静差跟踪控制，同时PR控制算法可以方便地实现谐波补偿，但同时它增大了系统阶数，增加了控制器的设计难度。文献[9]针对LCL型并网逆变器采用滞环控制，简单实用、稳定可靠、动态响应快、不依赖负载参数和无条件稳定，但其开关频率、损耗及控制精度受滞环宽度影响波动范围较大，导致滤波器设计困难，影响控制器的性能。文献[10]采用基于前馈补偿的解耦控制，有效消除了同步旋转坐标下LCL型并网逆变器数学模型d、q两轴之间存在复杂的耦合项，算法简单、技术成熟，但前馈解耦PI控制对并网电流难以达到理想的控制效果，存在稳态误差的问题。

针对LCL型并网逆变器的强耦合、非线性，采用逆系统控制方法，构造出原系统的逆系统，然后将构造出来的逆系统与原系统串联，将原系统线性化和解耦后，构成一个伪线性系统。 然后，针对这个伪线性系统设计滑模变结构控制器，设计方法变得简单易行。所采用的控制策略与基于前馈解耦PI控制方法相比，在设计控制器时， 控制器参数整定与PI控制器参数整定相比要简单。最后, 建立仿真模型进行仿真验证，仿真的结果证实了所提出的控制策略的正确性和有效性。

1 LCL型并网逆变器模型

图1为基于LCL滤波器的三相并网逆变器控制原理图。其中，直流母线电压Vdc由可再生能源提供，逆变后经LCL滤波器接至电网，通过调节逆变器输出电流实现并网供电。图中，L1为逆变器侧滤波电感；L2为电网侧电感；C为滤波电容；u、i分别为逆变器出口侧输出电压、电流；uc、ic分别为滤波电容电压和电流；ug为电网电压。由于电网容量较大，电网电压基本不变，因此并网逆变器输出的电能质量主要由并网电流ig决定。

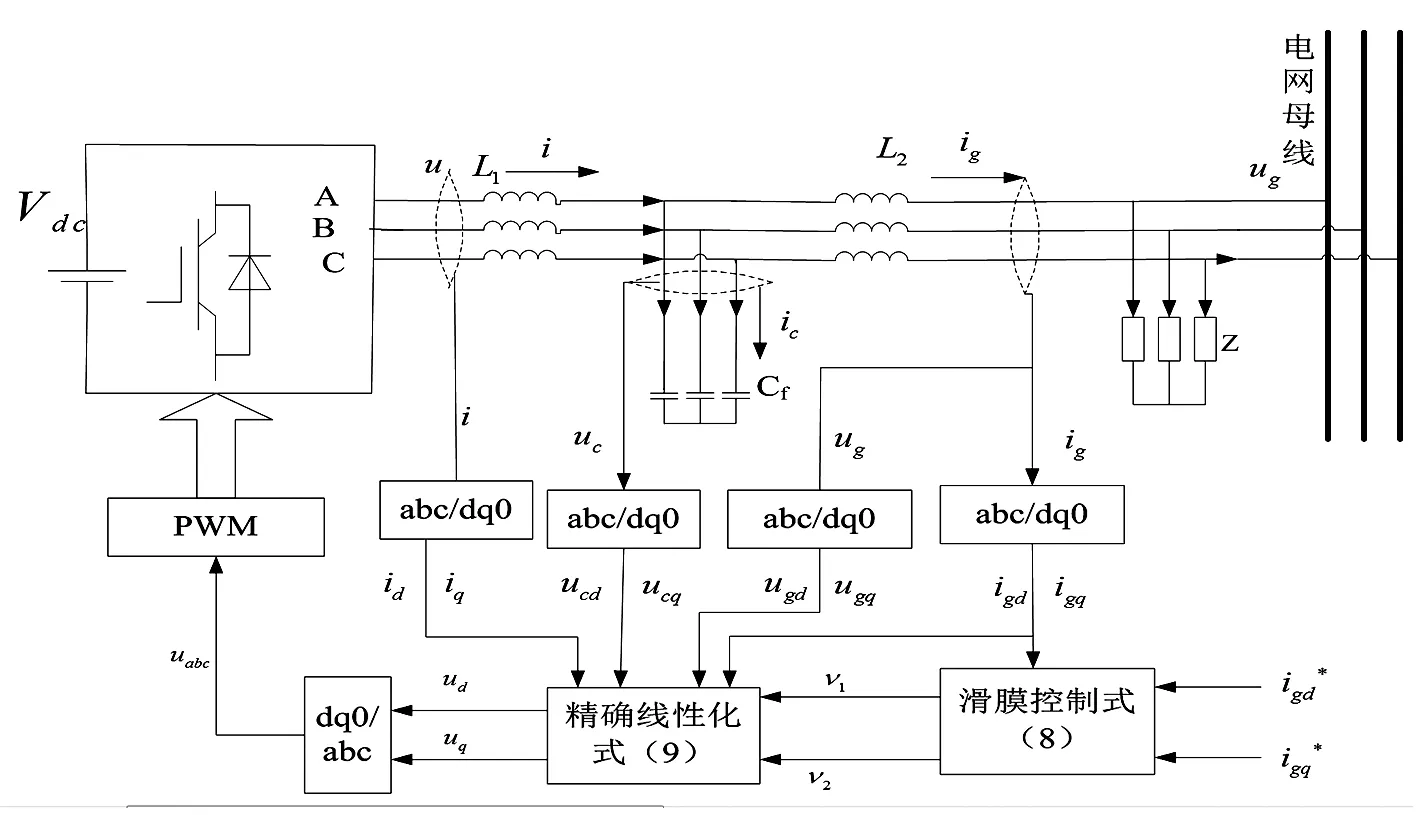
图1 滑模变结构控制图

三相LCL并网逆变器瞬时动态方程为

(1)

对式(1)作经典派克变换, 得到其在dq坐标下的数学模型为

(2)

在式(2)中：id、iq为逆变器出口侧输出电流的d、q轴分量；ud、uq为逆变器出口侧输出电压的d、q轴分量；ucd、ucq为滤波电容电压的d、q轴分量；igd、igq为逆变器并网电流的d、q轴分量。考虑到LCL并网逆变器为三相对称系统，那么各三相变量经派克变换后，其0轴分量均为0。根据式(2)所示的并网逆变器模型，可建立如下的多输入多输出系统：

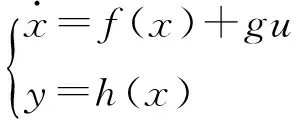
(3)

其中，系统的状态变量为x=[x1x2x3x4x5x6]T=[idiqucducqigdigq]T；输入变量为u=[u1u2]T=[uduq]T；输出变量为y=[y1y2]T=[igdigq]T。

由式(3)可以看出, 系统是一个多输入多输出的、强耦合的、非线性的系统。

2 LCL并网逆变器的控制策略

2.1 求取逆系统

逆系统方法[12]，是利用被控对象的逆系统将被控制对象补偿成具有线性传递关系的系统，即伪线性系统。然后,可灵活地运用各种控制理论来设计伪线性系统的控制器，构造两个独立的伪线性系统。对y1、y2求导，直到它们第1次含输入变量为止，结果如下：

(4)

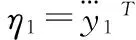
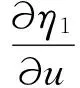
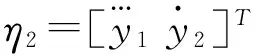
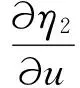
由逆系统相对阶定义可知，系统的相对阶为α=[α1α2]=[3 3]，α1+α2=6=n,n为系统阶数，故基于LCL滤波器的并网逆变器系统是完全可逆的。原系统线被性化解耦后， 所构成的伪线性系统可以解耦成2个子线性系统如下：

(5)

(6)

2.2 设计变结构控制器

变结构控制具有较强鲁棒性，它既可以用于设计线性系统，也可以用来设计非线性系统[13]。 但如果直接使用变结构控制设计非线性强耦合系统， 控制器设计会比较复杂，而采用逆系统方法将原系统线性化和解耦后，再采用变结构控制来分别设计各子系统则变得简单。因此，这里采用逆系统方法将系统线性化和解耦后，再运用变结构控制来设计控制器。

控制器设计目标：

e1=igd-igdref→0，e2=igq-igqref→0

根据变结构控制理论[13]，取切换面

(7)

用指数趋近律设计方法, 令

(8)

联合式(5)、式(6)、式(7)、式(8)可得两个伪线性系统的控制律为

(9)

将式(9)带入式(4)中，可得控制输入为

(10)

在式(9)、式(10)中：sgn()为符号函数；c11、c12、c21、c22、k1、k2、ε1、ε2为变结构控制器参数，均为正数。在保证系统不会发生振荡的条件下，适当地增大参数c11、c12、c21、c22、k1、k2较快的跟踪速度，而相应地减小参数ε1、ε2可以使系统减小抖动。

3 仿真分析

为验证所采用控制策略的可行性和有效性，在Matlab /Simulink中建立了如图1所示的模型，进行仿真验证，系统参数如表1所示。

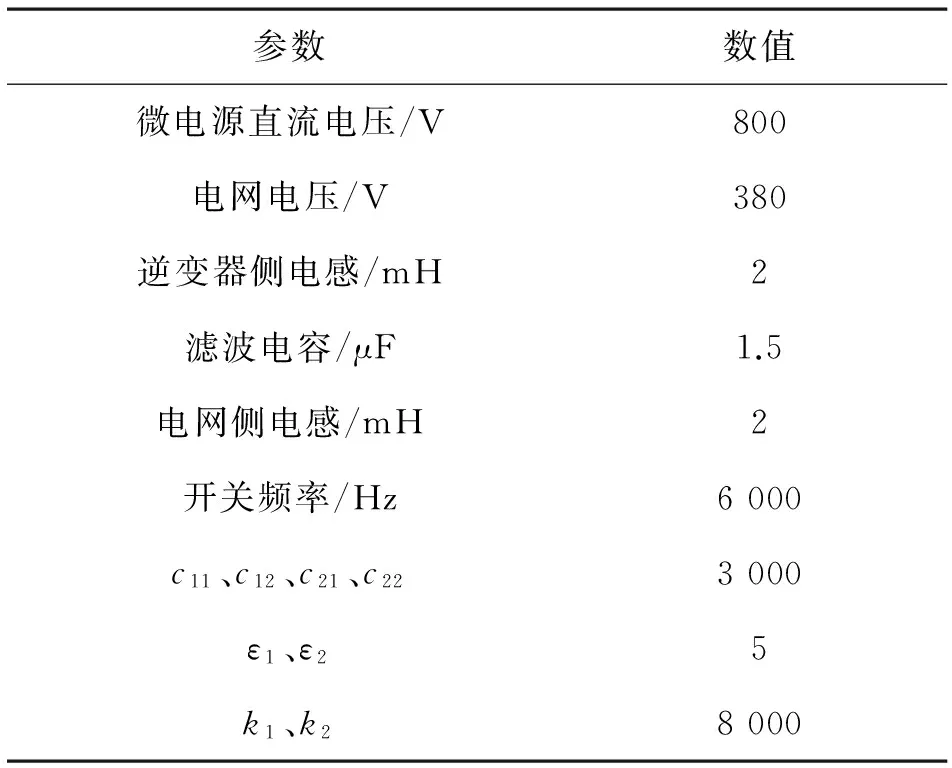
表1 系统参数

图2至图4给出了采用滑模变结构控制的动态响应曲线，图5至图7给出了采用传统前馈解耦PI控制方法下相应的动态曲线。

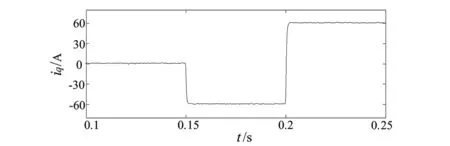
图2 滑模控制下无功电流波形

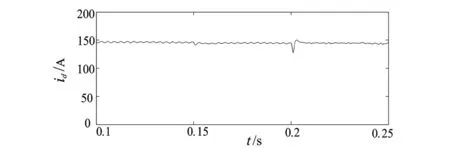
图3 滑模控制下有功电流波形

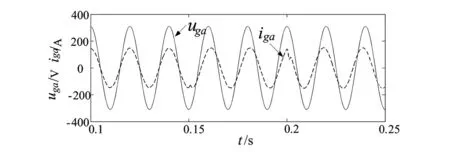
图4 滑模控制下a相电压和电流波形

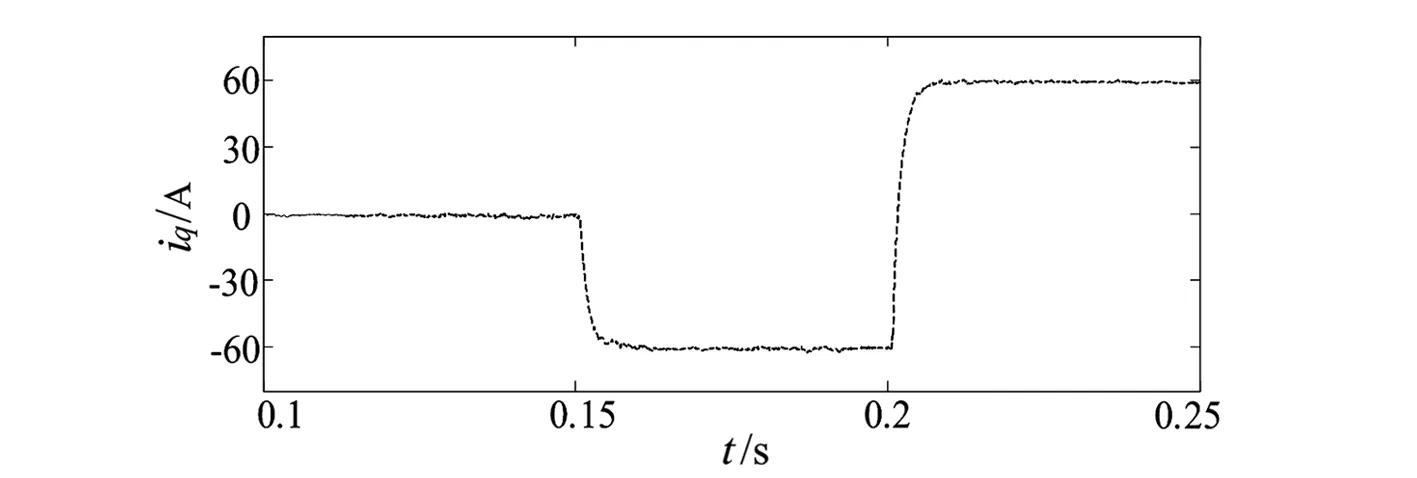
图5 PI控制下无功电流波形

图6 PI控制下有功电流波形

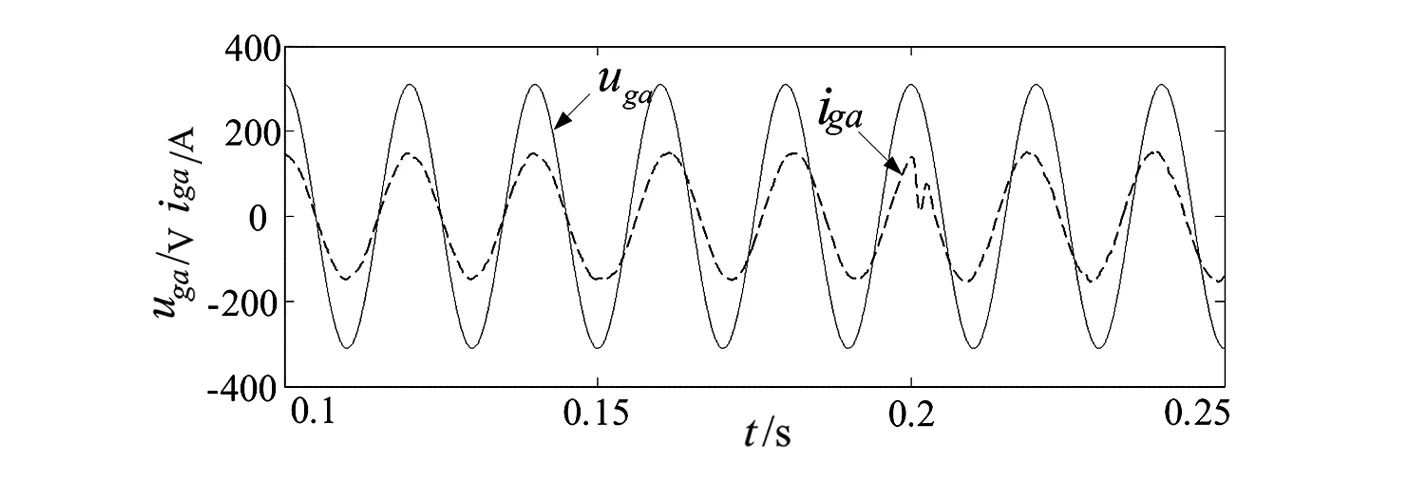
图7 PI控制下a相电压和电流波形

在0.15 s时，无功电流的指令值由0变为-60 A，在0.2 s时，又变为60 A。图2和图3分别为无功电流iq、有功电流id的仿真情况，分别与图5和图6对比，从图中可以看出，当电流给定值变化，采用滑模变结构控制时，并网电流响应曲线能够快速跟踪指令值的变化，超调量小，稳态无误差。图4是滑模变结构控制型a相电压和电流图，与图7比较可知，采用滑模变结构控制时，在并网电流突变时刻，a相电流更平滑，显示出很强的鲁棒性，能够有效减少并网电流的畸变率，提高入网电流质量。

4 结 语

前面阐述了LCL型并网逆变器的数学模型，并基于此数学模型，运用逆系统方法，将系统线性化和解耦后，分解成2个子线性系统；再采用滑模变结构控制，设计出各子系统控制器，来综合控制。这种控制方法与典型PI控制策略相比，其控制器参数更易于整定，无需附加阻尼电阻以保证系统稳定运行，而且仿真结果表明，变结构控制具有较快的响应速度，而且超调量小，具有更好的调节性能。算例证明了该控制策略的有效性。

[1] 许津铭,谢少军,张斌锋.分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J].中国电机工程学报,2015,35(16):4153-4166.

[2] 孙蔚,伍小杰，戴鹏，等.基于LCL滤波器的电压源型PWM整流器控制策略综述[J].电工技术学报,2008,23(1):90-96．

[3] Guoqiao S. An Improved Control Strategy for Grid-Connected Voltage Source Inverters with a LCL Filter[J]．IEEE Transactions on Power Electronics, 2008, 23(4):7.

[4] Liu F．Design and Research on Parameter of LCL Filter in Three-phase Grid-connected Inverter[C]．Power Electronics and Motion Control Conference,2009:2174-2177.

[5] 王要强,吴凤江,孙力,等.带LCL输出滤波器的并网逆变器控制策略研究[J].中国电机工程学报,2011,31(12):34-39.

[6] 郭小强,邬伟扬,顾和荣等.并网逆变器LCL接口直接输出电流控制建模及稳定性分析[J].电工技术学报,2010,25(3):102-109.

[7] Shen G. A New Current Feedback PR Control Strategy for Grid-connected VSI with an LCL Filter[C]. Applied Power Electronics Conference and Exposition，2009:1564-1569.

[8] Halimi,b. P A, Dahono．A Current Control Method for Phase-controlled Rectifier That Has An LCL Filter[C].2001 4th IEEE International Conference on Power Electronics and Drive Systems,2001:20-25.

[9] 戴训江,晁勤.基于LCL滤波的光伏并网逆变器电流滞环控制[J].电力电子技术,2009，43(71)：33-35.

[10] 屈克庆,叶天凯,赵晋斌，等. 基于前馈补偿的LCL型并网逆变器解耦控制策略研究[J].电气传动,2015,45(11)：26-30.

[11] 鲍陈磊,阮新波,王学华，等.基于PI调节器和电容电流反馈有源阻尼的LCL 型并网逆变器闭环参数设计[J].中国电机工程学报,2012,32(25):133-142.

[12] 戴先中.多变量非线性系统的神经网络逆系统控制方法[M].北京:科学出版社,2005．

[13] 高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996.

According to the operating characteristics of three-phase grid-connected distributed generation system and the work characteristics of LCL filter, the mathematical model of three-phase grid-connected inverter is established. Its mathematical model in a synchronous rotatingdqcoordinate system reflects that it is a strong coupling nonlinear system. To avoid the difficulties in designing the controllers for the system, an inverse-system control is proposed. Firstly, using the inverse-system method, the original system is linearized and decoupled into a pseudo-linear system. Secondly, employing the variable-structure control (VSC) theory, the variable-structure controllers of the pseudo-linear system is designed for controlling the system of grid-connected inverter with LCL filter. Finally, the feasibility and effectiveness of the proposed control strategy are verified by the simulations on Matlab/Simulink.

LCL filter; inverse-system; variable-structure control; robustness

TM85

A

1003-6954(2017)03-0056-05

李 鹏(1992)，硕士研究生，研究方向为微电网与新能源发电技术、滑模变结构控制；

2017-01-27)

王 奔(1960)，教授、博士，研究方向为研究方向为电力系统非线性和变结构控制。