基于AHP的工业工程专业课程量化评价

蔡志强

摘要：研究人员已经提出了不同的方法来评估课程的研究过程。最终，研究人员认为需要将人的因素、个人的经验、直觉和判断考虑在研究范畴内。为了验证这一点，文章利用定量层次分析法（Analytic Hierarchy Process，AHP）的基础模型，来评估西北工业大学工业工程系中的专业课程。文章把层次分析法引入系统，将其作为一个解决方案，用于处理主观评估。层次分析法已被用于构建所有课程的替代方案，在层次结构中，对那些影响因素和产生的分数进行评估。

Abstract： Researchers have proposed different methods to evaluate the curriculum of the research process. Ultimately， the researchers believe that the implications of the study including human factors， personal experience， intuition and judgment. In order to verify this point，based on the principle and method of analytic hierarchy process （AHP）， this paper evaluates the professional course in the department of industrial engineering， Northwestern Polytechnical University. In this paper， the AHP is introduced into the system， as a solution， to deal with subjective evaluation. AHP has been used to build alternatives for all curricula， in the hierarchy， evaluate the impact factors and the resulting scores.

关键词：工业工程专业课程；量化评价；AHP

Key words： industrial engineering courses；quantitative assessment；AHP

中图分类号：G642 文献标识码：A 文章编号：1006-4311（2017）19-0235-03

0 引言

工程教育作为一个发展中的领域，有着一门进行着科学改革学科的许多特点。随着学习部门整体教学质量的提高，学生能力和课程实验受到的关注也越来越高。工业工程课程旨在提供一个工业工程的综合教育，并平衡教学的广度和深度，以培养有能力的工程师为教学目的[1]。解决学生在课程中遇到的问题，一直是教师的一个主要问题。定量评估是一套评价标准，我们可以用它来找出这些困难；层次分析法通过一组评价标准和一组可选择的替代方案的比较，从而得到最好的结论[2]。本文的目的是将定量工具与层次分析法相结合，并将其改进整理。

在发达国家，工业工程改革尚不很充分，工业工程项目在发展中国家也没有得到很好的发展[3]。在过去的十年中，欧洲和美国工业工程发展非常迅速[4]。具有高工艺性能和柔性机械的产品使生产更为复杂[5]。质量功能展开法的应用使得中东的大学中很多教学教育质量得以提升[6]。设计和规划工程教育也能够提高工程专业学生的教育质量和满意度。

自上个世纪中叶以来，许多大学推出了课程评估，以应对社会对某些专业的需求变化，进而满足生产过程中组织目标和质量目标的要求。由于上述变化与学生遇到的问题有关，因此，本文的主要问题是如何提高工业工程专业本科生的教育质量，以及如何确定该解决方案是在大多数情况下是有效的。

1 课程评估层次结构设计

层次分析法是一个用来衡量确定的与不确定的、有形的与无形的、明确的与模糊的等定量与定性相容的决策方法。由于它在处理复杂决策问题上的实用性和有效性，很快在世界范围得到重视和广泛应用。其应用已遍及经济计划与管理、能源政策与分配、，教育、人才、医疗卫生和环境等领域。

为了有效地对课程进行评估，需要AHP的准则层和方案层进行确定。在评估过程中，有许多因素会对课程评价产生影响和作用。目标层是对课程进行评估。准则层分类时，可以借用几种常用的方法来确定被分解的结构，如头脑风暴、备忘录、失效模式等。通过上述方法，目标层被分为3组来考虑，具体分为任课教师，大一、大二的学生和大三、大四的学生。在这一层面，教师是第一组学生（大一和大二）和第二组（大三和大四）的最重要的影响因素。针对第一准则层，根据相应人员的经验和对工业工程课程的建议与了解，可分为6类。根据“What-if”分析模型，可以发现23门在西北工业大学未开设的课程可以作为方案层。最终，可以得到课程评估的层次结构模型，如图1。

针对任课教师和学生，由于他们的经历和对工业工程专业的认识不同，相应得到的二级准则也不相同，下面对二级准则层中各因素的含义进行说明，如表1所示。

建立了课程评估的层次结构之后，需要得到方案相对于目标层的权重，最终得到课程的优先级排序，并得到西北工业大学工业工程课程改革的方案。

2 權重和一致性检验

2.1 平均权重的计算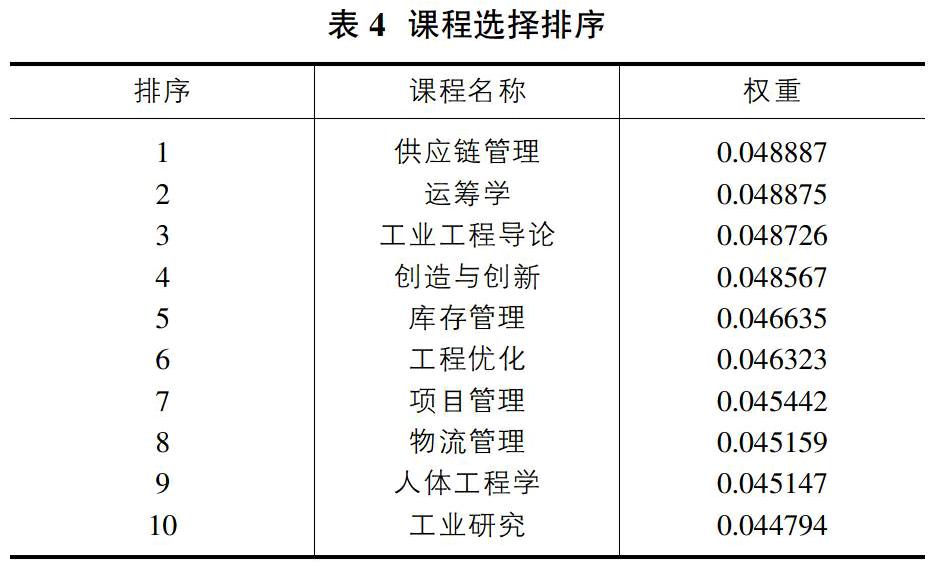

平均权重在计算时需要借助判断矩阵C，判断矩阵中的元素满足Cij=1Cji，则平均权重的计算方法如下：

2.2 一致性检验

为了使数据更加可信，需要对得到的权重和判断矩阵进行一致性检验，只有一致性检验满足条件，才能借助AHP进行求解，如果不满足一致性条件则需要对判断矩阵中的参数进行调整。下面对一致性检验的方法进行说明：

2.3 判断矩阵的生成

当准则层中的因素进行两两比较时，由于重要性的差别，会使得判断矩阵中的元素值存在差别。Nicola Rossi和Jean Michelez在ALTRAN在2001年提出的判断矩阵中元素确定的规则，在所有不同的标准平均值之间计算误差，并根据表3中误差百分比的大小给更重要的因素定义为大于1，而不重要的因素对应的大小则是该值的倒数。

3 各级准则层的层次分析

本文选取了西北工业大学工业工程专业四个年级中的77名同学以及7位教师填写调查问卷，获得原始数据。根据问卷中答案的逻辑关系以及前后是否具有一定的线性相关关系对回收问卷进行筛选，除掉23份无效学生问卷，最终得到有效问卷共计61份。

3.1 一级准则层的层次分析

对于一级准则，根据行政部门老师对任课教师相对于第一组学生和第二组学生的影响，计算相应平均值，结合表3得到相应的判断矩阵。同样的根据2.1中的方法计算出任课教师和两组学生的权重；根据2.2中的方法可以对判断矩阵的一致性进行检验。

利用计算机软件matlab2012a计算得到任课教师的权重为0.6434，第一组学生的权重为0.0738，第二组学生的权重为0.2828。在一致性检验过程中，得到一致性检验指标的值为0.0563，小于0.1，满足一致性条件，所以该判断矩阵可以接受。

3.2 二级准则层的层次分析

在二级准则层中，对于任课教师和学生的影响因素不同；同时，第一组学生相对于第二组学生在相同因素的影响下，也会有不同的决策。因此在这一部分需要对任课教师、第一组和第二组学生分别进行层次分析。

3.2.1 任课教师影响因素的层次分析

对任课教师的6个影响因素，需要进行两两比较，计算相应平均值，结合表3得到相应的判断矩阵。根据2.1的方法计算得到教师和两组学生的权重；根据2.2的方法对判断矩阵的一致性进行检验。

利用计算机软件matlab2012a计算得到6个因素在二级准则的权重分别为0.3411， 0.3411， 0.0224， 0.1083， 0.1162， 0.0709。乘以相应的一级权重0.6434可以得到全局权重。在一致性检验过程中，得到一致性检验指标的值为0.0949，小于0.1，满足一致性条件，所以该判断矩阵可以接受。

3.2.2 第一组学生影响因素的层次分析

对第一组学生的6个影响因素，需要进行两两比较，计算相应平均值，结合表3得到相应的判断矩阵。根据2.1的方法计算得到教师和两组学生的权重；根据2.2的方法对判断矩阵的一致性进行检验。

利用计算机软件matlab2012a计算得到6个因素在二级准则的权重分别为0.1282， 0.4366， 0.2462， 0.0367， 0.0242， 0.1282。乘以相应的一级权重0.0738可以得到全局权重。在一致性检验过程中，得到一致性检验指标的值为0.0876，小于0.1，满足一致性条件，所以该判断矩阵可以接受。

3.2.3 第二组学生影响因素的层次分析

对第二组学生的6个影响因素，需要进行两两比较，计算相应平均值，结合表3得到相应的判断矩阵。根据2.1的方法计算得到教师和两组学生的权重；根据2.2的方法对判断矩阵的一致性进行检验。

利用计算机软件matlab2012a计算得到6个因素在二级准则的权重分别为0.1731， 0.3342， 0.3342， 0.0462， 0.025， 0.0872。乘以相应的一级权重0.2828可以得到全局权重。在一致性检验过程中，得到一致性检验指标的值为0.0465，小于0.1，满足一致性条件，所以该判断矩阵可以接受。

3.3 方案层的层次分析

对于方案层有23门可供选择的工业工程课程，需要得到每个课程在相应的一级准则下的权重，然后计算23门课程的全局权重，并从中选取权重较大的课程，作为课程改革的重点。

首先，以任課教师对23门课的问卷数据为例，来计算每门课程在相应的评定准则下的方案层权重。在计算过程中通过统计7名教师的问卷数据，算得23门课在各个准则下的平均数；然后将所有数据进行归一化，方法与2.1中相同；最终将归一化之后的矩阵与任课教师评定7中准则的全局权重相乘，即能得到最终的方案层权重。

对于两组学生的计算方法与教师相同，在此不再赘述，最终可以得到23门课程的全局权重。

4 AHP结果分析

通过对AHP分析得到的权重结果进行分析，所有值进行筛选，选出其中权重靠前的10门课程，并对这10门课程进行重点分析，如表4。不难看出，在今后西北工业大学工业工程课程改革需要重点考虑如下10门课程：供应链管理、运筹学、工业工程导论、创造与创新、库存管理、工程优化、项目管理、物流管理、人体工程学、工业研究等。

5 结论

基于AHP的工业工程专业定量化评估方法，借助AHP对西北工业大学工业工程学科的建设进行评估，并得到了相应的改进方案，有针对性地增加国外工业工程名校的课程。最后，通过统计得到具有代表性学科的学习方式。基于AHP的工业工程专业定量化评估方法会对工业工程教学改革提供有力的保障。

参考文献：

[1]杨琴，王语诗，陈泞.基于学生视角优化工业工程专业实践教学[J].实验室研究与探索，2016（8）：228-231.

[2]朱克毓，董庆兴，梁昌勇，等.一类三角模糊层次分析法的无效性分析[J].系统工程理论与实践，2015（8）：2104-2112.

[3]江志斌.论新时期工业工程学科发展[J].工业工程与管理， 2015（1）：1-7.

[4]Palma M， Ríos I D L， Guerrero D. Higher Education in Industrial Engineering in Peru： Towards a New Model Based on Skills[J].Procedia - Social and Behavioral Sciences， 2012， 46（1）：1570-1580.

[5]Volkmann J W， Landherr M， Lucke D， et al. Engineering Apps for Advanced Industrial Engineering[J]. Procedia Cirp， 2016， 41（3540）：632-637.

[6]Ksal G， Man A. Planning and design of industrial engineering education quality[C]// Selected Papers From the， Icc&ie Conference on Computers & Industrial Engineering. Elsevier Science Ltd. 1998：639-642.