非正态分布数据的过程能力分析方法

王雪情

摘要：非正态过程能力分析的方法的研究一直以来广受关注。简要介绍了三种不同的计算非正态数据的过程能力指数的方法后，针对现有研究的不足，分别使用三种不同的方法计算过程能力指数，然后根据计算结果做出了分析和比较，最后将得到的结论应用到实际中进行分析，研究表明：虽然进行非正态分布数据的过程能力分析的方法很多，但是正态性转换的方法不具有稳健性，而非参数的方法的精度虽然不高，但对任何一种分布都是可以使用的。

Abstract： Process capability analysis of the non-normal is becoming an imperative problem. In this paper， three different methods of calculating the process capability index of non-normal data are briefly introduced. Based on the shortcomings of existing research， the process capability index is calculated by three different methods， and then the analysis and comparison are made according to the calculation results. Finally， the conclusions will be applied to the actual analysis. Although there are many ways to estimate process capability of non-normal data， results of the first two ways is not robust. Meanwhile， the parameters are not limited to any kind of distributions whose result is low accuracy.

關键词：非正态分布；过程能力指数；Minitab

Key words： non-normal distribution；process capability index；Minitab

中图分类号：F224.0 文献标识码：A 文章编号：1006-4311（2017）19-0209-05

0 引言

过程能力指数（Process Capability Index，PCIs）是用来度量过程能力的相对高低。它开始是由朱兰提出的，是用公差范围和过程能力的商值表示，可以用来估计任何时间的过程能力指数[1]。但是过程能力分析一般要求数据服从正态分布。但是搜集的数据并不都服从正态分布，所以对于非正态分布数据的过程能力分析变成了一个棘手的问题。

本文介绍了三种不同的计算方法，并对比分析了它们的优劣性，并通过实际案例的分析验证了该结果的有效性。本文是通过Minitab软件来辅助分析的。

1 非正态分布数据的过程能力计算方法

1.1 Box-Cox转换法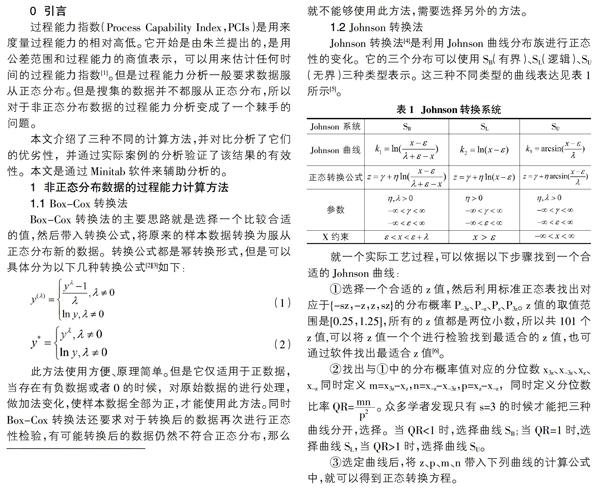

此方法使用方便、原理简单。但是它仅适用于正数据，当存在有负数据或者0的时候，对原始数据的进行处理，做加法变化，使样本数据全部为正，才能使用此方法。同时Box-Cox转换法还要求对于转换后的数据再次进行正态性检验，有可能转换后的数据仍然不符合正态分布，那么就不能够使用此方法，需要选择另外的方法。

1.2 Johnson转换法

Johnson转换法[4]是利用Johnson曲线分布族进行正态性的变化。它的三个分布可以使用SB（有界）、SL（逻辑）、SU（无界）三种类型表示。这三种不同类型的曲线表达见表1所示[5]。

就一个实际工艺过程，可以依据以下步骤找到一个合适的Johnson曲线：

①选择一个合适的z值，然后利用标准正态表找出对应于{-sz，-z，z，sz}的分布概率P-3z、P-z、Pz、P3z。z值的取值范围是[0.25，1.25]，所有的z值都是两位小数，所以共101个z值，可以将z值一个个进行检验找到最适合的z值，也可通过软件找出最适合z值[6]。

②找出与①中的分布概率值对应的分位数x3z、x-3z、xz、x-z同时定义m=x3z-xz，n=x-z-x-3z，p=xz-x-z，同时定义分位数比率QR=。众多学者发现只有s=3的时候才能把三种曲线分开，选择。当QR<1时，选择曲线SB；当QR=1时，选择曲线SL，当QR>1时，选择曲线SU。

③选定曲线后，将z、p、m、n带入下列曲线的计算公式中，就可以得到正态转换方程。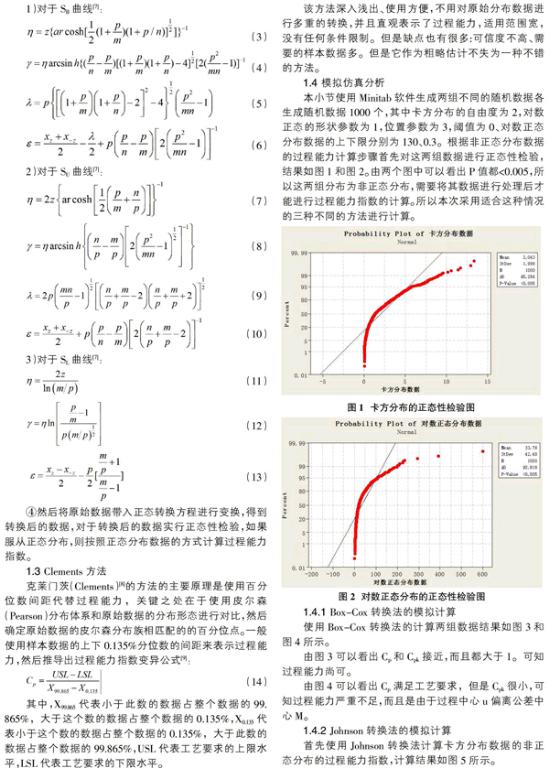

④然后将原始数据带入正态转换方程进行变换，得到转换后的数据，对于转换后的数据实行正态性检验，如果服从正态分布，则按照正态分布数据的方式计算过程能力指数。

1.3 Clements方法

克莱门茨（Clements）[8]的方法的主要原理是使用百分位数间距代替过程能力，关键之处在于使用皮尔森（Pearson）分布体系和原始数据的分布形态进行对比，然后确定原始数据的皮尔森分布族相匹配的的百分位点。一般使用样本数据的上下0.135%分位数的间距来表示过程能力，然后推导出过程能力指数变异公式[9]：

其中，X99.865代表小于此数的数据占整个数据的99.865%，大于这个数的数据占整个数据的0.135%，X0.135代表小于这个数的数据占整个数据的0.135%，大于此数的数据占整个数据的99.865%，USL代表工艺要求的上限水平，LSL代表工艺要求的下限水平。

该方法深入浅出、使用方便，不用对原始分布数据进行多重的转换，并且直观表示了过程能力，适用范围宽，没有任何条件限制。但是缺点也有很多：可信度不高、需要的样本数据多。但是它作为粗略估计不失为一种不错的方法。

1.4 模拟仿真分析

本小节使用Minitab软件生成两组不同的随机数据各生成随机数据1000个，其中卡方分布的自由度为2，对数正态的形状参数为1，位置参数为3，阈值为0、对数正态分布数据的上下限分别为130、0.3。根据非正态分布数据的过程能力计算步骤首先对这两组数据进行正态性检验，结果如图1和图2。由两个图中可以看出P值都<0.005，所以这两组分布为非正态分布，需要将其数据进行处理后才能进行过程能力指数的计算。所以本次采用适合这种情况的三种不同的方法进行计算。

1.4.1 Box-Cox转换法的模拟计算

使用Box-Cox转换法的计算两组数据结果如图3和图4所示。

由图3可以看出Cp和Cpk接近，而且都大于1。可知过程能力尚可。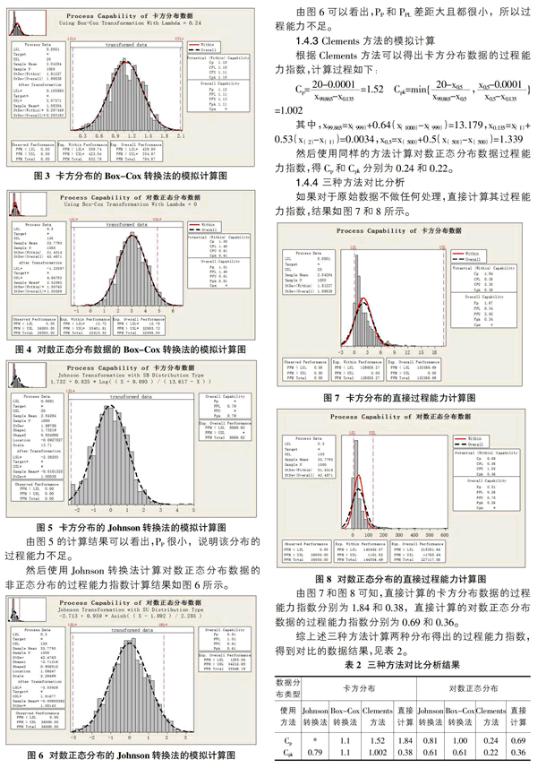

由图4可以看出Cp满足工艺要求，但是Cpk很小，可知过程能力严重不足，而且是由于过程中心u偏离公差中心M。

1.4.2 Johnson转换法的模拟计算

首先使用Johnson转换法计算卡方分布数据的非正态分布的过程能力指数，计算结果如图5所示。

由图5的计算结果可以看出，PP很小，说明该分布的过程能力不足。

然后使用Johnson转换法计算对数正态分布数据的非正态分布的过程能力指数计算结果如图6所示。

从两组随机数据特征可以看出数据都在上下限范围内，所以理论上过程能力应该很高，但是Johnson转换法和Box-cox转换法必须判断它们是否能够将数据转换成正态分布的数据，如果不能转换，那方法就会失效。但是如果能够转换的前提下，这两种方法所获得的精确度将比Clements方法高。Clements方法使用虽然没有任何的限制条件，但是它计算的能力指数变化较大，稳健性不强。

2 实证研究

2.1 案例介绍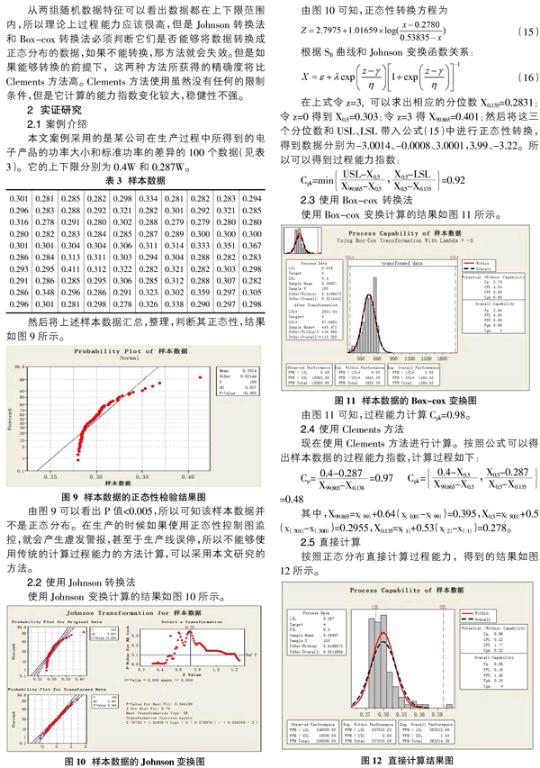

本文案例采用的是某公司在生产过程中所得到的电子产品的功率大小和标准功率的差异的100个数据（见表3）。它的上下限分别为0.4W和0.287W。

由图12可知，過程能力计算Cpk=0.22。

2.6 结果分析

本章通过实际案例的研究，利用Box-cox转换法和Johnson转换法得到了两个相似的结果，而使用Clements方法得出的结果明显比这两个正态性转换的方法得到的结果小，但是这三个结果和直接计算的结果Cpk=0.22都有差距。

所以这三种方法都具有有效性。而由于该公司行业领先水平，所以其过程能力应该不错，就本例来说，直接按照正态分布进行计算得到的过程能力指数很小，说明工作严重不足，而按照本研究提出的方法得到的过程能力指数比较好，工艺过程符合实际生产水平，这就符合该公司所代表的质量水平。所以在进行实际生产的过程能力评估的时候，应该尊重实际数据的分布规律，以免给生产工艺水平造成误判。

参考文献：

[1]何桢，吴静，孔祥芬.基于Johnson转换的非正态分布过程能力研究[J].组合机床与自动化加工技术，2007（8）：104-107.

[2]孔祥芬.非正态过程能力分析与控制方法研究[D].天津大学，2007.

[3]梁涛.模拟集成电路性能参数建模及其参数成品率估计算法的研究[D].西安电子科技大学，2013.

[4]刘瑞，刘洪伟.基于蒙特卡洛模拟的非正态数据过程能力研究[J].标准科学ISTIC，2012（11）.

[5]石文华，陈春良，吴宇华.基于Johnson转换的轴承装配过程质量控制[J].火力与指挥控制，2012，37（12）：48-54.

[6]贾颖君.制药过程中非正态数据的分析[J].黑龙江医药， 2013，26（6）：66-68.

[7]杨洁荣，宋向东，明喆，胡蓓蓓，王树力.基于两种转换的非正态过程能力研究的比较[J].统计与决策，2011（6）：165-166.

[8]Clements J A.Process capability calculations for non-normal distributions [J].Quality Progress，1989，22：95-100.

[9]Yum B J， Kim K W. A bibliography of the literature on process capability indices： 2000–2009[J]. Quality and Reliability Engineering International， 2011， 27（3）： 251-268.