位值制
文︳张新春
位值制
文︳张新春
讨论位值制,我们应先区分位值制与进位制。事实上,相对于位值制而言,进位制出现得更早,更普遍。从某种意义上说,进位制是对刻痕记数的直接改进——刻痕记数,数是多少就刻多少道痕,对大数尤其是比较大的数而言,显然不方便,于是很容易想到进位制。所谓进位制,就是以P个数组成一个新的单位,用一个新的符号表示。P个新的单位又组成一个更高的单位,用另一个符号表示。我们就把这个叫做P进制。P叫做进位的基。“如不算最原始的刻痕记数,古今中外的记数法都是进位制的”(梁宗巨,《世界数学通史》,辽宁教育出版社),而位值制则是在进位制的基础上,对如何处理新的单位想到了漂亮的办法。以下即详述这种办法。
我们不难发现,前面叙述的加法累数制的罗马记数和乘法累数制的中国记数有一个共同特点:新的单位必须创造新的名称——无论是罗马的“X”和中国的“十”,都是表示新的单位的符号。而位值制的漂亮在于不需要创造新的符号表示新的单位。比如,表示“20”,不需要写成“XX”或“二十”,只需要把表示“2”的符号写到表示“十”的位置上即可。同样是这个“2”,还可以表示“200”,或“2000”……一个数码表示什么数值,就看它在什么位置上,这就是位值的含义。
中国算筹记数与位值制雏形

中国算筹记数法非常接近位值制。古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为13~14cm,径粗0.2~0.3cm,多用竹子制成。也有用木头、兽骨、象牙、金属等材料制成的。大约二百七十几根为一束,放在一个布袋里,系在腰间随身携带,需要记数和计算时就取出来。
在算筹记数法中,以纵横两种排列方式表示单位数目,其中1~5分别用纵横方式排列相应数目的算筹表示,6~9则以上面的算筹加下面相应的算筹表示,此时上面的一根表示5(如下图所示)。
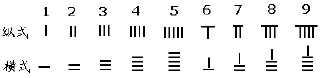
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,依此类推,遇零则置空。据《孙子算经》记载,算筹记数法是“凡算之法,先识其位,一纵十横,百立千僵,千十相望,万百相当”。《夏阳侯算经》说“满六以上,五在上方,六不积算,五不单张”。纵式和横式的区别,再加上个位必用纵式的规定,较好地解决了空位的问题。比如,3740与374,如果没有这样的规定,用算筹摆出来就没什么区别。再如,3704用算筹摆为:,由于7和4都是用的纵式,考虑到纵横相间的规定,我们可以肯定7和4之间有一个0。而则表示374。
从这些例子可以看出,除了数码的表现形式不同外,中国算筹记数已经和现在的十进位值制没什么两样。特别是,后来为了明确起见,规定用○表示空位,就几乎与现在的记数方法完全一样了(值得说明的是,尽管有了纵横相间和个位用纵式的规定,还是无法使算筹的摆法与所记的数形成一种一一对应的关系,比如,除了表示3704外,说它表示370004也无不可。当然,这两者相差近百倍,根据所表示的数的实际意义或上下文进行理解也许不会产生混淆。但从理论上看,这是一个问题,于是,零这个符号“○”的发明成为必要)。
十进位值制
十进位值制记数法就是以10为基的位值制记数法。现在,我们用通用的阿拉伯数字0、1、2、3、4、5、6、7、8、9表示前几个自然数。一个大的自然数,比如,四千五百七十八可以表示为:4000+500+70+8=4×103+5×102+7×10+8的形式,在十进位值制记数法中,这个数就用“4578”表示。
一般地,就整数而言,十进位值制通过“逢十进一”,把一个正整数从右到左分成个位、十位、百位、千位等,每个数位上的计数单位分别为一、十、百、千……,即依次为100,101,102,103……。十进位值制表示一个数的通用方式为:N=ak×10k+ak-1× 10k-1+…+a1×101+a0×100。其中a0,a1,a2,…,ak∈{0,1,2,3,4,5,6,7,8,9}且ak≠0。这种形式的N可简记为akak-1ak-2·…·a1a0。若对每个ai都指定了具体的数,则上述记号中的横线省略不写。规定最高位不能为0是为了保证这种表示方式的唯一性。显然,如果最高位可以是0,25就可以写成025或0025,数的表示方式就不唯一了。在这种表示法之下,我们也称N为k+1位数。很显然,0不符合这种表示方式(因为0的最高位就是0),因此,我们通常不说0是几位数。自然数中,最小的一位数是1。需要了解的是,“位数”这样的概念概括的不是数的本质特征,而是与记数法有关的形式特征。以5为例,在十进位值制记数法之下,它是一位数;若在二进制记数法之下,它就记为1012,成为三位数了。
如前面所述,当前通用的数字为阿拉伯数字,但使用何种数字却并非十进位值制的实质。比如,我们可以用零、一、二、……九表示,4785就表示为“四七八五”。事实上,阿拉伯数字刚传到欧洲,即引起当时的大数学家斐波拉契的高度关注。他在其名著《算盘书》中写道:“这里的印度9个数字9,8,7,6,5,4,3,2,1,还有一个阿拉伯人称之为零的符号0,可以把任何数表示出来,实在是一种理想的计数符号。”正是基于这种认识,他号召欧洲人用这种数字取代罗马数字。随后又经过诸多曲折,阿拉伯数字终于在16世纪得到广泛的应用。
位值制记数法最重要的优点之一就是便于计算。“其计算规则可以用这些数字的加法表和乘法表的形式来表示,而且一旦记住,便可永远运用自如。古代的计算技巧一度只限于少数专家所掌握,而现在则是小学里的课程了。像这样的科学进步对日常生活有如此深刻影响,并带来极大方便的例子还不是很多”([美]R·柯朗,H·罗宾,《什么是数学》,复旦大学出版社,2008)。
在加法交换律和结合律的支持下:
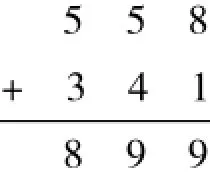
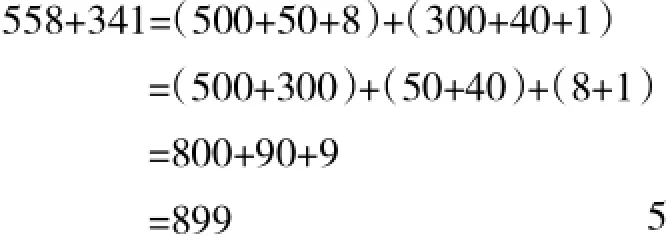
而这一切又可写成一种更简单的形式(如右所示)。
于是,在十进位值制记数法之下,在运算定律的支持下,任意两个数相加,通过以上竖式的计算程序(法则),可以转化成一系列20以内加法的组合。而20以内的加法原则上都是需要记忆的。因此,在20以内加法的教学过程中,不管我们如何确定教学目标,“接受”“记忆”是必须的方法。一定的计算速度是必要的目标,不能简单地将“接受”和“记忆”等同于“落后”。
对于乘法,也完全类似。有了十进位值制记数法,在乘法交换律、结合律以及分配律的支持下,任意两数相乘都可以通过一定的程序(法则)转化为一系列表内乘法和加法的组合。这里的程序(法则)可以用我们熟悉的乘法竖式表示,而表内乘法正如20以内的加法一样,都是需要记忆的。于是,乘法口诀的教学也一样,其最根本的目标是口诀能脱口而出。
数学教育的真功夫是对数学与数学教育的把握,唯此才能成就好的数学课堂。湖南数学教师的老朋友,《湖南教育》的申建春老师开通了微信公众号“与数学老师谈心”,请关注。


