余能原理基面力元法在桁架弹塑性分析中的应用

李瑞雪，彭一江

(北京工业大学建筑工程学院，北京 100124)

余能原理基面力元法在桁架弹塑性分析中的应用

李瑞雪，彭一江

(北京工业大学建筑工程学院，北京 100124)

基面力元法(BFEM)是一种新型的有限单元法，是以"基面力"来描述一点的应力状态。为了编制适用于桁架弹塑性分析的MATLAB基面力元程序，以余能原理基面力元法为基础，将基面力元法的平面4节点的实体单元模型向桁架单元进行退化，列出了退化桁架单元的柔度矩阵、单元轴力和节点位移的具体表达式，并对其控制方程进行了必要的处理。根据退化的桁架单元模型，采用增量法的思想和线性强化弹塑性模型，以三杆超静定桁架和复杂静定桁架为算例进行了计算。将计算结果与大型有限元分析软件ABAQUS的T2D2计算结果进行了对比分析，发现所用方法与ABAQUS的计算结果高度吻合，进一步验证了基面力理论的正确性和程序的适用性。

塑性力学；有限单元法；基面力元法；余能原理；桁架；弹塑性分析

有限单元法[1]从正式提出至今已经历了半个多世纪的发展。在过去的几十年中，以节点位移作为基本未知量的“位移型有限元”，因其清晰易懂的物理概念率先被发展并得到广泛应用[2]，它是以最小势能原理作为理论基础，而且要求它所采用的离散化结构必须满足位移协调性。但是随着日益发展的需要，待解决的问题也越来越多样化和复杂化。不同的有限元模型，例如基于最小余能原理的平衡元[3]、杂交元[4]、非协调元[5]以及广义协调元[6]等被一大批学者提出并被研究。因此，针对有限元问题探索具有更简洁的应力和变形描述体系，建立不依赖网格且收敛性好的新型有限元模型是一些学者所关心的。

2003年，GAO[7]提出了一个描述应力状态的新概念——“基面力(base force，BF)”,该基面力为一阶张量，可以像其他传统的二阶张量一样来描述一点的应力状态，其表达公式简洁，推导方程方便。在高玉臣[8-9]工作的基础上，彭一江[10]开始了基于基面力概念的新型有限元研究，分别对平面问题、空间问题和弹性大变形问题建立了相应的基面力元模型，并于2009年将该方法简称为“基面力元法(BFEM)”[11]。经过近几年的研究，基面力元法理论已经不断地应用在许多领域中[11-13]，其相关研究工作也引起了国际同行的关注与研究[14-16]。

本文以余能原理基面力元法为基础，对平面4节点的实体单元模型[17]进行退化，得到了平面2节点的桁架基面力元模型，推导了其柔度矩阵的具体表达式，并进一步对控制方程进行了处理。利用增量法的思想和MATLAB编程语言，编制了桁架的弹塑性基面力元程序，结合典型的平面桁架算例进行了数值计算，验证了该模型的正确性。

1 桁架单元的基面力元模型

1.1 柔度矩阵

对于平面问题，考虑如图1所示的平面4节点单元。I，J，K和L分别表示单元4个边的边中节点，TI，TJ，TK和TL分别为作用在相应节点上的力，也称单元面力。

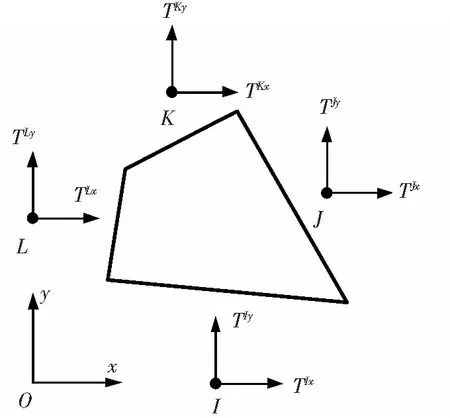
图1 平面4节点单元Fig.1 Four-node plane element

单元的柔度矩阵可表示为

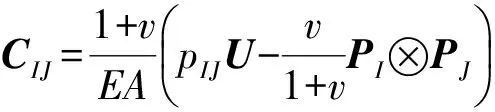
I,J=1,2,3,4。

(1)

退化的平面桁架单元如图2所示，假设应力均匀的分布在整个杆单元中，α，β分别表示单元的第α节点和第β节点，且α，β=1，2；Tα,Tβ为作用在第α节点和第β节点上的力。

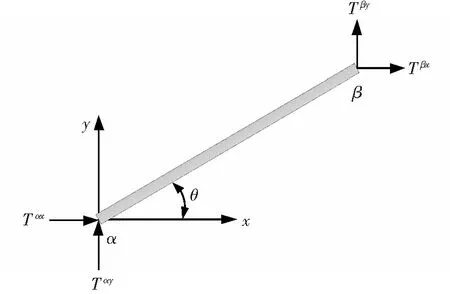
图2 平面桁架单元Fig.2 Planar truss element

从桁架结构的基本假设上说，不考虑其剪切能力，而泊松比的本质是对剪切效果的研究，所以单纯的桁架结构分析不需要泊松比也可以求解出其轴向的力学响应，所以本文假设泊松比v=0，于是桁架单元的余能可写为

(2)

平面桁架单元的柔度矩阵也可由平面4节点单元退化为

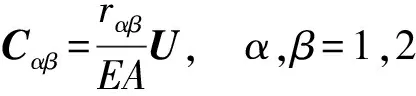
(3)

式中：A为单元的面积；U为单位张量。Pαβ为单元的第α节点和第β节点的径矢rα和rβ的点积，有

U=ex⊗ex+ey⊗ey,

(4)

rαβ=rα·rβ=rαxrβx+rαyrβy。

(5)

最终可以得到Cαβ的具体形式

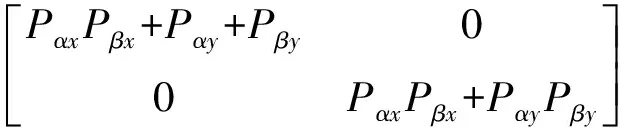
(6)

1.2 单元轴力表达式

根据文献[17]，基线力Tα与Cauchy应力张量σ的关系式为

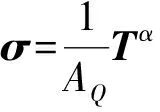
(7)

由于桁架单元中假设只有轴力，且其应力在整个杆中都是均匀分布的，单元的应力可写为

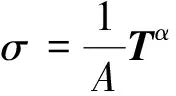
(8)

本文计算轴力的思路一开始是在求出杆端面力后沿着轴线方向合成得到，后来考虑到桁架不存在剪力，推断其轴力必是沿轴线方向的主应力与横截面积的乘积，并且验证了推断的正确性，所以有

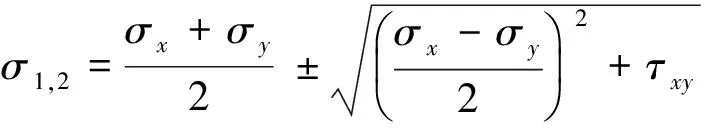
(9)

轴力取不为零的主应力与横截面积的乘积，有

(10)

式中Acs为杆单元的横截面面积。

1.3 控制方程及其处理

余能基面力元的控制方程可以写成

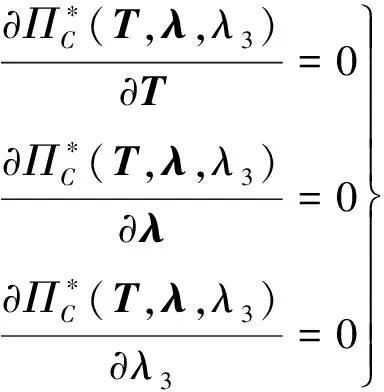
(11)

式(11)的第1式的物理意义是位移协调条件，主要包括：1)不同单元在连接节点处的相对位移为零；2)单元的位移要满足边界条件。

式(11)的第2式的物理意义是各单元力的平衡，即每个单元2个节点的力加起来为零。

式(11)的第3式的物理意义是各单元转动的平衡，即每个单元2个节点的力绕原点的力矩之和为零。

对于之前研究的平面实体单元，每个公共边界由于只包含2个单元，可由计算机自动判别并赋予两单元接触边上大小相等、方向相反的单元面力T和-T，从而满足这一约束条件。而对于桁架结构来说，每个公共节点至少包含2个及以上的多个单元，此时未知力的个数也会相应增加，各个未知力不能再简单设置为等大反向。假如有n个杆交于一点，则需要假设的未知力数是n-1个。

桁架结构的上述特点，导致控制方程与基面力元实体单元主要有两点不同之处：1)必须考虑各个杆在交点处力的平衡；2)各个杆在交点处的位移协调，即各个杆的相对位移为零。

考虑一个由m个公共节点组成的杆系结构，其部分系统与公共节点i相连的n个杆件及其节点荷载如图3所示。

图3 部分杆系系统Fig.3 Partial rods system

根据交点处力的平衡条件，有

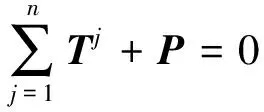
(12)

对于i节点来说，须设有n-1个未知力，第n个杆的力Tn可由其他杆的力来表示，即

Tn=-P-T1-T2-…-Tn-1。

(13)

各杆在交点处的位移协调条件由式(11)的第1式表示，对上述的部分杆系系统可展开为

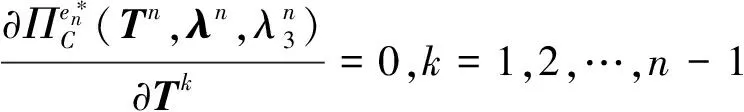
(14)

式(14)表达的物理意义可以理解为第k根杆与第n根杆在相对位移为零，即n根杆是连在一起的。

1.4 节点位移表达式

桁架结构节点I的位移δI可由该点所包含的任意一个单元的支配方程求得，其表达式为

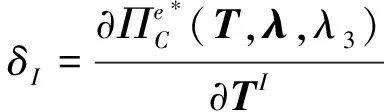
(15)

可得到节点位移δI的显式表达式

δI=CIJ·TJ+λ+λ3ε·rI。

(16)

其矩阵形式可写为

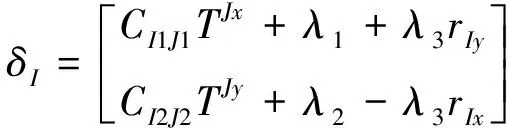
(17)

根据推导的基面力元公式和控制方程，并且采用增量法的思想和线性强化弹塑性模型，编制出了适用于平面桁架弹塑性分析的MATLAB程序。在程序的每一个增量步的计算中，假定方程组是线性的，柔度矩阵也是常数，那么，每步施加一个荷载增量ΔP，得到一个位移增量Δδ，累计后即得到最终的位移。

2 算 例

本文算例采用的材料本构是线性强化弹塑性模型，为研究方便，取各杆的杨氏模型为210GPa，屈服极限为250MPa，并服从Mises屈服条件，屈服后的弹性模量取为42MPa，各杆的横截面积取单位10cm2。

2.1 三杆超静定桁架

平面三杆超静定桁架的单元尺寸和所受荷载如图4所示。将应用本文编制的MATLAB基面力元程序计算该算例，求得的单元轴力解和节点位移解与ABAQUS的计算结果进行对比，并分别列于表1和表2。

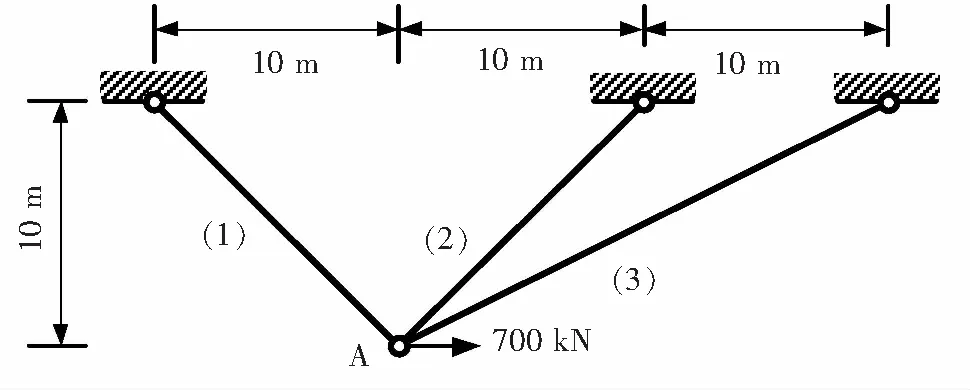
图4 三杆超静定桁架的弹塑性分析Fig.4 Elastic-plastic analysis of three bar statically indeterminate truss

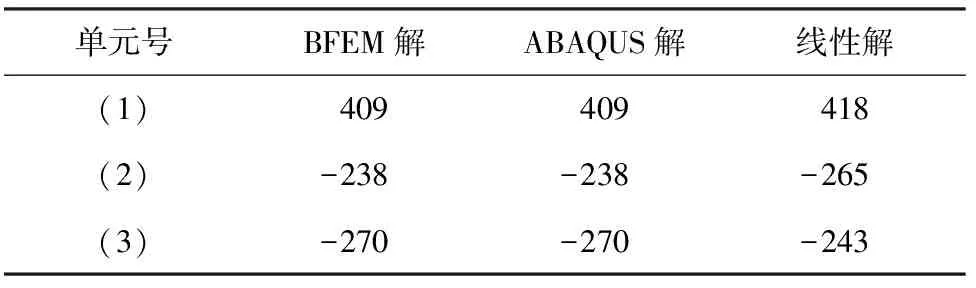
kN

表2 节点位移

从表1中可以看出，(1)单元和(2)单元均率先进入了塑性阶段，表2中也可以看出，A点产生了较大的塑性位移。本文对加载后的三杆桁架进行卸载，并将卸载后A节点的位移值与ABAQUS的计算结果对比列于表3。

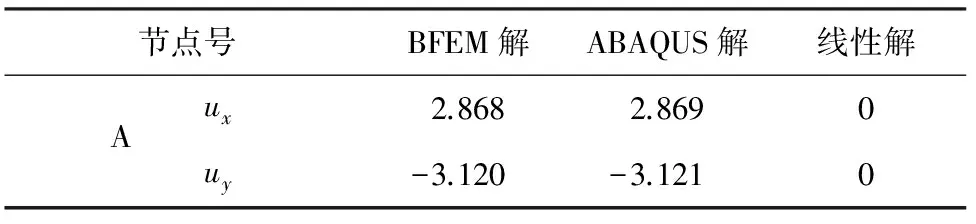
表3 卸载后的节点位移

最后给出了A点荷载与位移的关系，如图5所示。

图5 A点荷载与位移关系曲线Fig.5 Curves between displacement and load at node A

由表1—表3可知，应用弹塑性基面力元程序计算的轴力和位移解与ABAQUS的计算结果高度吻合。荷载和位移的关系曲线图也比较符合理论情况。

2.2 复杂静定桁架

平面复杂静定桁架的单元尺寸和所受荷载如图6所示。将应用本文编制的MATLAB基面力元程序计算该算例，求得的单元轴力解和节点位移解与ABAQUS的计算结果进行对比，并分别列于表4和表5。

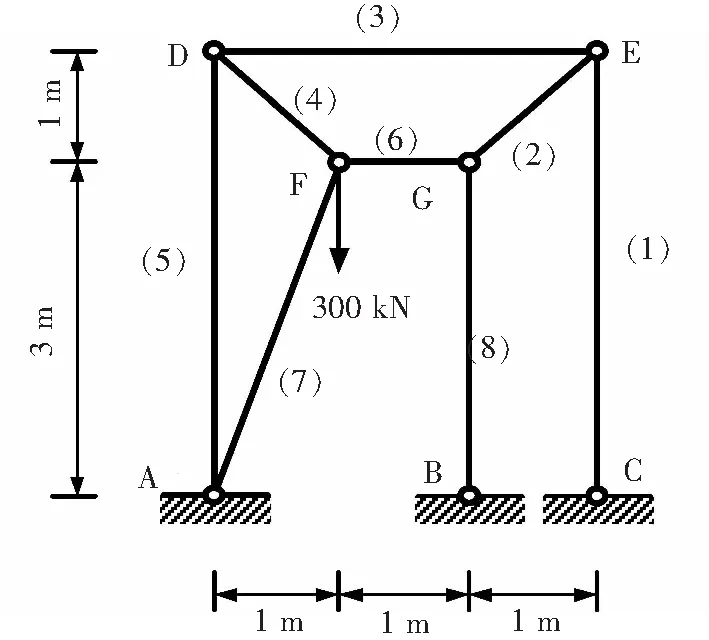
图6 复杂静定桁架的弹塑性分析Fig.6 Elastic-plastic analysis of complex statically determinate truss

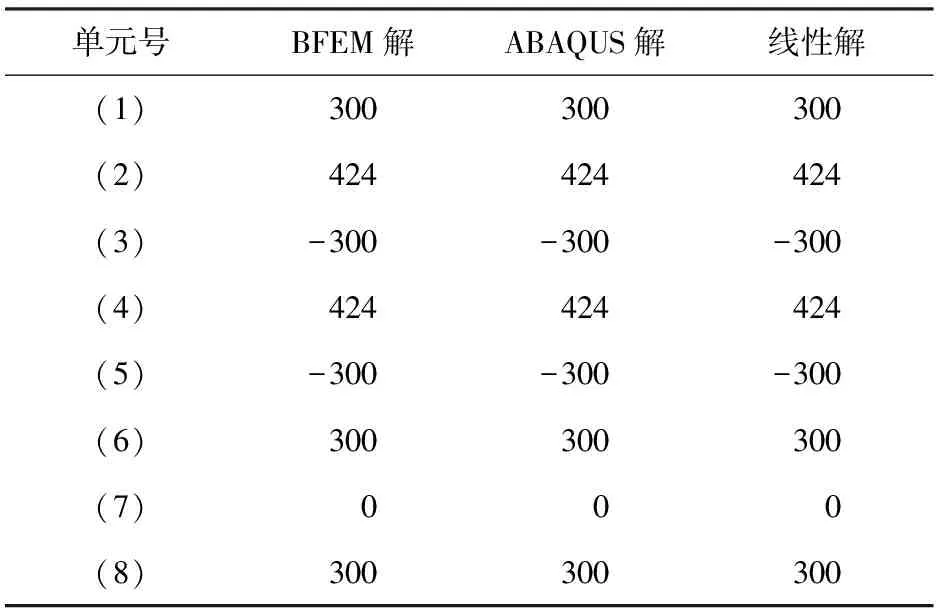
kN

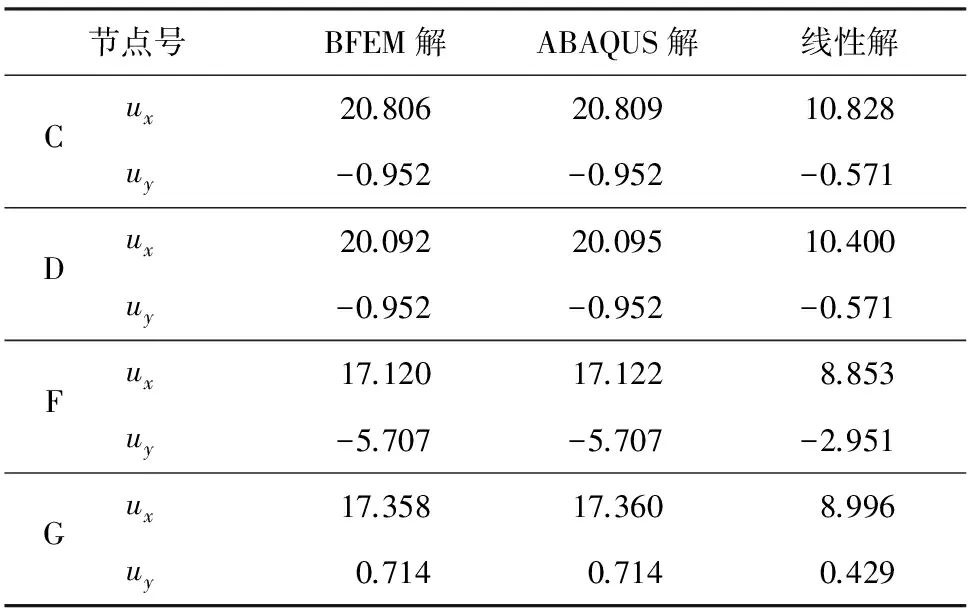
表5 节点位移

对加载后的复杂桁架算例进行卸载，将卸载后各节点的位移值与ABAQUS的计算结果列于表6。

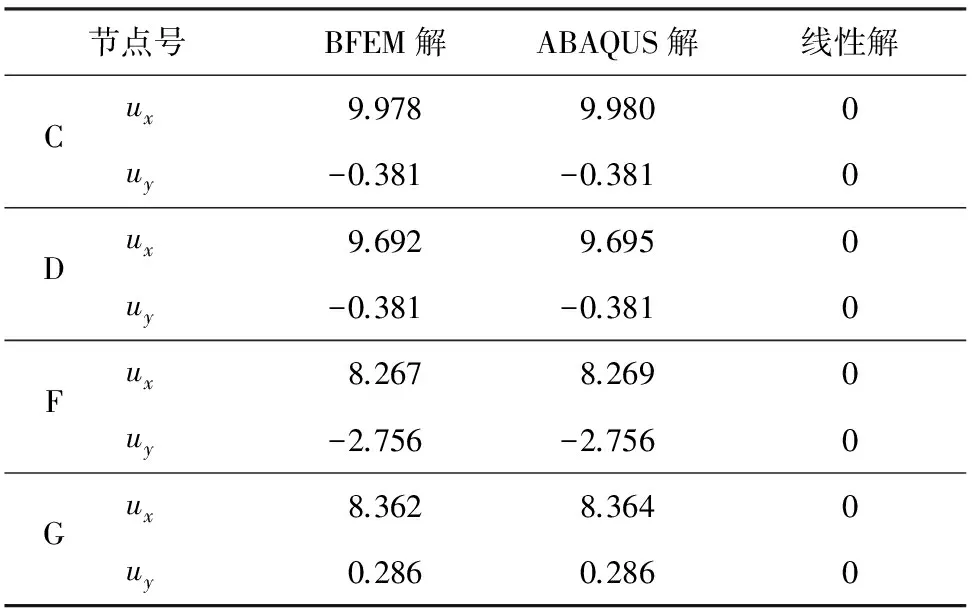
表6 卸载后的节点位移

最后给出了F点荷载与位移的关系，如图7所示。

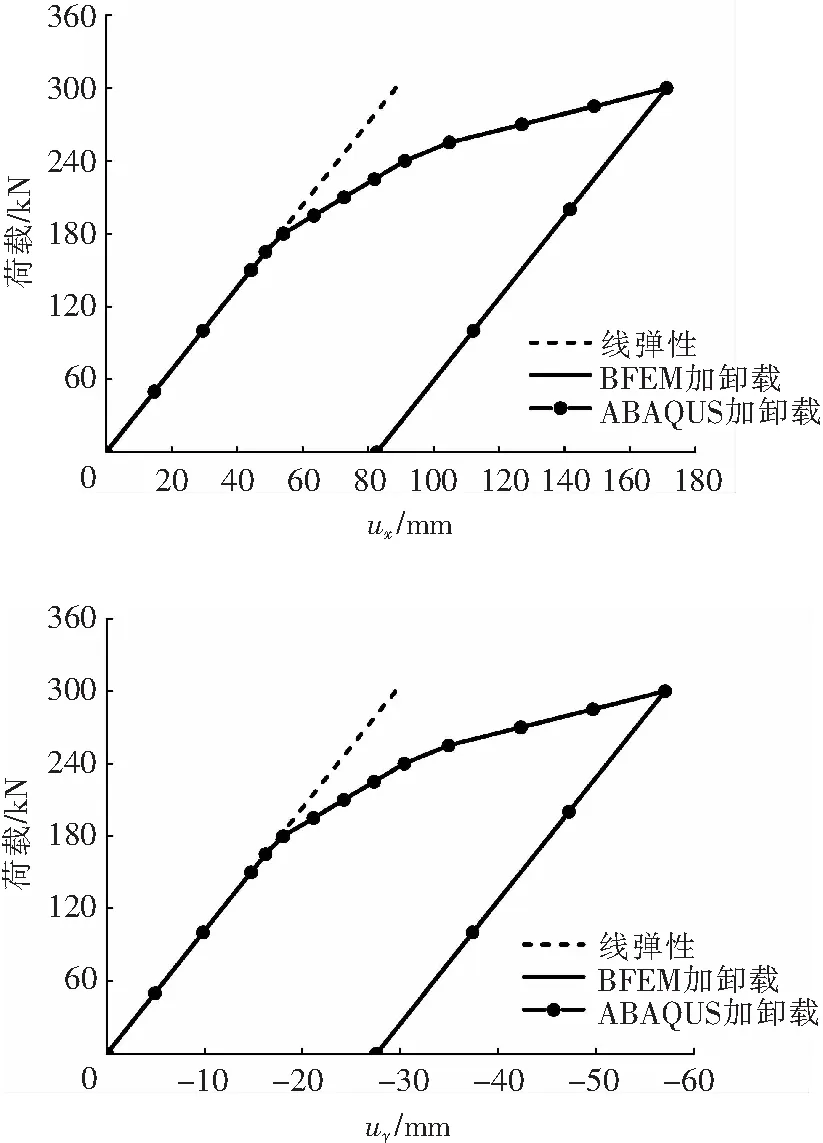
图7 F点荷载与位移关系曲线Fig.7 Curves between displacement and load at node F

由表4—表6可知，应用弹塑性基面力元程序计算的轴力和位移解与ABAQUS的计算结果高度吻合。荷载和位移的关系曲线图也比较符合理论情况。

3 结 论

本文把增量法的思想应用于平面桁架单元的余能原理基面力元模型中，编制了能够对平面桁架进行弹塑性分析的MATLAB程序。与传统的位移型有限元模型相比，该计算程序误差较小，具有较高的精度。同时发现，在本文柔度矩阵、轴力以及位移的求解中均不用进行局部坐标系与整体坐标系的转换。表明以基面力作为基本未知量的桁架基面力元模型的简洁性和相应程序的适用性，进一步丰富和完善了余能原理在桁架中的应用，同时也表明了基面力元理论的正确性和广泛的应用前景。

/References:

[1] CLOUGH R W. The finite element method in plane stress analysis[J]. Proceedings of American Society of Civil Engineers, 1960, 23: 345-378.

[2] WASHIZU K. Variational Methods in Elasticity and Plasticity[M]. 2nd ed. New York:Pergamon Press, 1975.

[3] VEUBEKE B F D. Displacement and equilibrium models in the finite element method[J]. International Journal for Numerical Methods in Engineering， 1965, 9(3):145-197.

[4] PIAN T H H,CHEN D P, KANG D. A new formulationof hybrid/mixed finite element[J]. Computers & Structures， 1983, 16(1/2/3/4): 81-87.

[5] WILSON E L, TAYLOR R L, DOHERTY W P, et al. Incompatible displacement models[J]. Numerical and Computer Methods in Structural Mechanics, 1973, 43-57.

[6] 龙驭球.新型有限元论[M].北京：清华大学出版社，2004.

[7] GAO Y C. A new description of the stress state at a point with applications[J].Archive of Applied Mechanics， 2003, 73(3): 171-183.

[8] 高玉臣.固体力学基础[M].北京：中国铁道出版社，1999.

[9] 高玉臣.弹性大变形的余能原理[J].中国科学G辑:物理学、力学、天文学， 2006，36(3)：298-311. GAO Yuchen. Complementary energy principle for large elastic deformation[J].Science in China(Series G. Physics, Mechanics & Astronomy, 2006, 36(3): 298-311.

[10]彭一江.基于基面力概念的新型有限元方法[D].北京:北京交通大学,2006. PENG Yijiang. A New Finite Element Method Based on the Concept of Base Force[D]. Beijing: Beijing Jiaotong of Technology, 2006.

[11]PENG Yijiang, LIU Yinghua. Base force element method of complementary energy principle for large rotation problems[J]. Acta Mechanica Sinica, 2009, 25(4): 507-515.

[12]张昭锋.基于余能原理的基面力元法在岩体力学中的应用[D]. 北京：北京工业大学,2014. ZHANG Zhaofeng. The Application of Base Force Element Method on Complementary Energy Principle in Rock Mechanics[D]. Beijing:Beijing University of Technology, 2014.

[13]王耀.三维基面力元法及其在再生混凝土细观损伤分析中的应用[D].北京：北京工业大学,2015. WANG Yao. Research of Three-Dimensional Base Force Element Method and Application on Meso-Demage Analysis for Recycled Concrete[D]. Beijing: Beijing University of Technology, 2015.

[14]SANTOS H A F A, PIMENTA P M, ALMEIDA J P M. A hybrid-mixed finite element formulation for the geometrically exact analysis of three-dimensional framed structures[J]. Computational Mechanics,2011, 48: 591-613.

[15]SANTOS H A F A. Variationally consistent force-based finite element for the geometrically non-linear analysis of Euler-Bernoulli framed structures[J]. Finite Elements in Analysis and Design, 2012, 53: 24-36.

[16]SANTOS H A F A. A novel updated Lagrangian complementary energy-based formulation for the elastica problem: force-based finite element model[J]. Acta Mechanica,2015, 226(4): 1133-1151.

[17]彭一江,雷文贤,彭红涛.基于基线力概念的平面4节点余能有限元模型[J].北京工业大学学报,2009,35(11)：1484-1490. PENG Yijiang, LEI Wenxian, PENG Hongtao. Four-node plane element model on complementary energy based on the concept of base line forces[J]. Journal of Beijing University of Technology, 2009,35(11)：1484-1490.

Application of base force element method with complementary energy principle for elasto-plastic truss analysis

LI Ruixue, PENG Yijiang

(College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)

Base force element method(BFEM) is a new type of finite element method, which uses the "base force" as fundamental variables to describe the stress state at a point. In order to compile a base force element program for the elasto-plastic analysis of truss using MATLAB language, based on the BFEM with complementary energy principle, the solid element of the plane 4 nodes in BFEM is degenerated into the truss element. The concrete expressions of the flexibility matrix, axial force and displacement of the degenerated truss elements are derived, and necessary modification of the governing equations is conducted. According to the degenerated truss element model, the idea of incremental method and linear strengthened elasto-plastic model are adopted for calculation by using 3-pole indeterminate truss and complicated static determinacy as samples. It is found that through comparison of the calculated results and the results from T2D2 of ABAQUS, the calculated results using the method are in highly agreement with those obtained with ABAQUS, which further verifies the correctness of the base force element method and the applicability of the program.

plastic mechanics; finite element method; base force element method(BFEM); complementary energy principle; truss; elasto-plastic analysis

1008-1534(2017)04-0276-06

2017-04-07;

2017-04-27；责任编辑：陈书欣

国家自然科学基金(10972015)

李瑞雪(1991—)，男，河北邯郸人，硕士研究生，主要从事余能原理基面力元法方面的研究。

彭一江教授。E-mail：pengyijiang@bjut.edu.cn

O344

A

10.7535/hbgykj.2017yx04008

李瑞雪，彭一江.余能原理基面力元法在桁架弹塑性分析中的应用[J].河北工业科技,2017,34(4):276-281. LI Ruixue, PENG Yijiang.Application of base force element method with complementary energy principle for elasto-plastic truss analysis[J].Hebei Journal of Industrial Science and Technology,2017,34(4):277-281.