尺寸参数对横向稳定杆侧倾刚度的影响分析及验证
王晓莲,张学博
(中国第一汽车股份有限公司技术中心,吉林长春 130011)
尺寸参数对横向稳定杆侧倾刚度的影响分析及验证
王晓莲,张学博
(中国第一汽车股份有限公司技术中心,吉林长春 130011)
在横向稳定杆开发设计过程中,尺寸参数的选择直接影响横向稳定杆的侧倾刚度。稳定杆的侧倾刚度受多个尺寸参数的影响,计算公式复杂,初始设计阶段很难通过公式直观判断参数如何选择。根据理论计算,绘制单一参数对横向稳定杆侧倾刚度的影响曲线,可直观判断不同参数对横向稳定杆侧倾刚度的影响程度。结合国内、外横向稳定杆产品的实际尺寸参数,通过对比分析,验证了绘制的尺寸参数影响曲线的正确性,解决了横向稳定杆设计初期尺寸参数难以准确选择和优化的问题。
横向稳定杆;侧倾刚度;尺寸参数;影响曲线
0 引言
横向稳定杆是防止汽车在转弯时发生过大的横向侧倾、保持汽车平衡的悬架系统重要零件,可提高车辆的操纵稳定性,提升舒适性和安全性[1-2]。在稳定杆设计过程中,各尺寸参数的选择需要考虑对稳定杆侧倾刚度的影响,同时根据整车布置空间进行调整。各尺寸参数对稳定杆侧倾刚度的影响程度不尽相同,在稳定杆设计时需要综合考虑。稳定杆侧倾刚度计算公式非常复杂,设计初期很难通过公式直观判断尺寸参数如何选择。文中通过绘制各尺寸参数对稳定杆侧倾刚度的影响曲线,可以直观地了解不同尺寸参数对稳定杆侧倾刚度的影响幅度,能够在稳定杆设计时准确、直观、方便地进行尺寸参数选择和优化。
1 直角形横向稳定杆侧倾刚度理论计算公式
直角形横向稳定杆侧倾刚度计算简图如图1所示。
影响横向稳定杆侧倾刚度的基本尺寸参数为:L1、L2、L3、R、d。
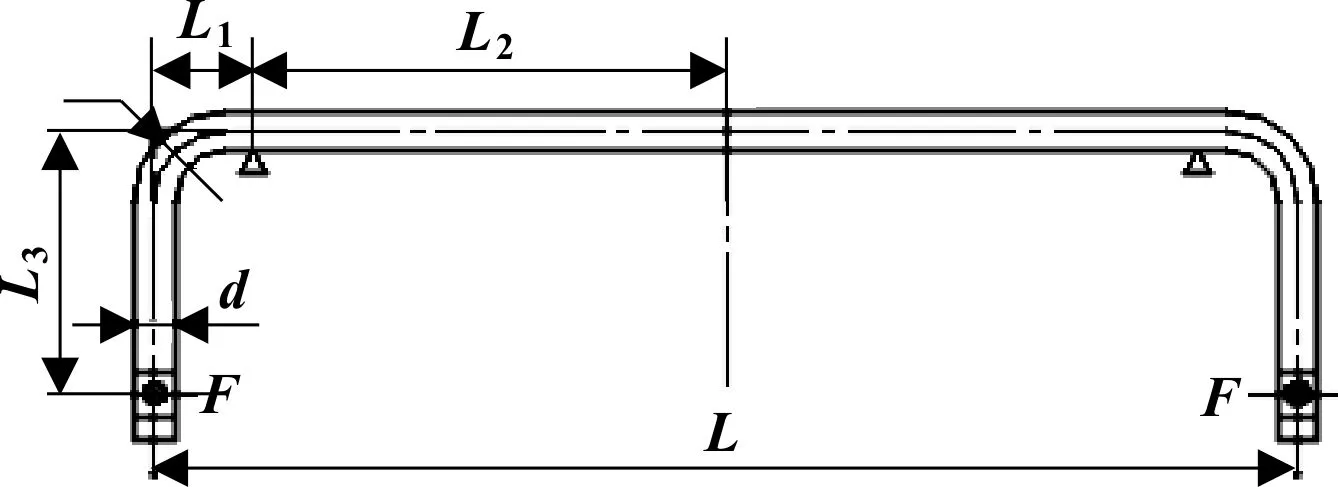
图1 直角形横向稳定杆示意图
直角形横向稳定杆侧倾刚度的计算公式[3-4]为:
(1)
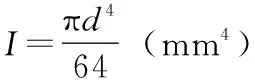
根据能量原理,推导出公式(1)中的P和U如下:
(2)
(3)
稳定杆基本尺寸参数如表1所示。

表1 稳定杆基本尺寸参数表 mm
根据公式(1),绘制基本尺寸参数L1、L2、L3、R、d对横向稳定杆侧倾刚度的影响曲线。
2 基本尺寸参数
2.1 尺寸参数L1的影响曲线
保证稳定杆总长L不变,即L=1 000 mm不变。L1取点情况如表2所示。绘制尺寸参数L1对横向稳定杆侧倾刚度的影响曲线,如图2所示。
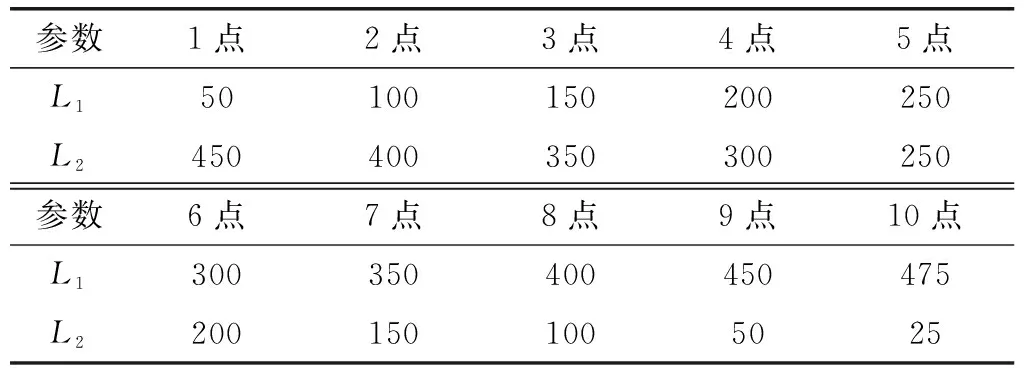
表2 L1取点表 mm
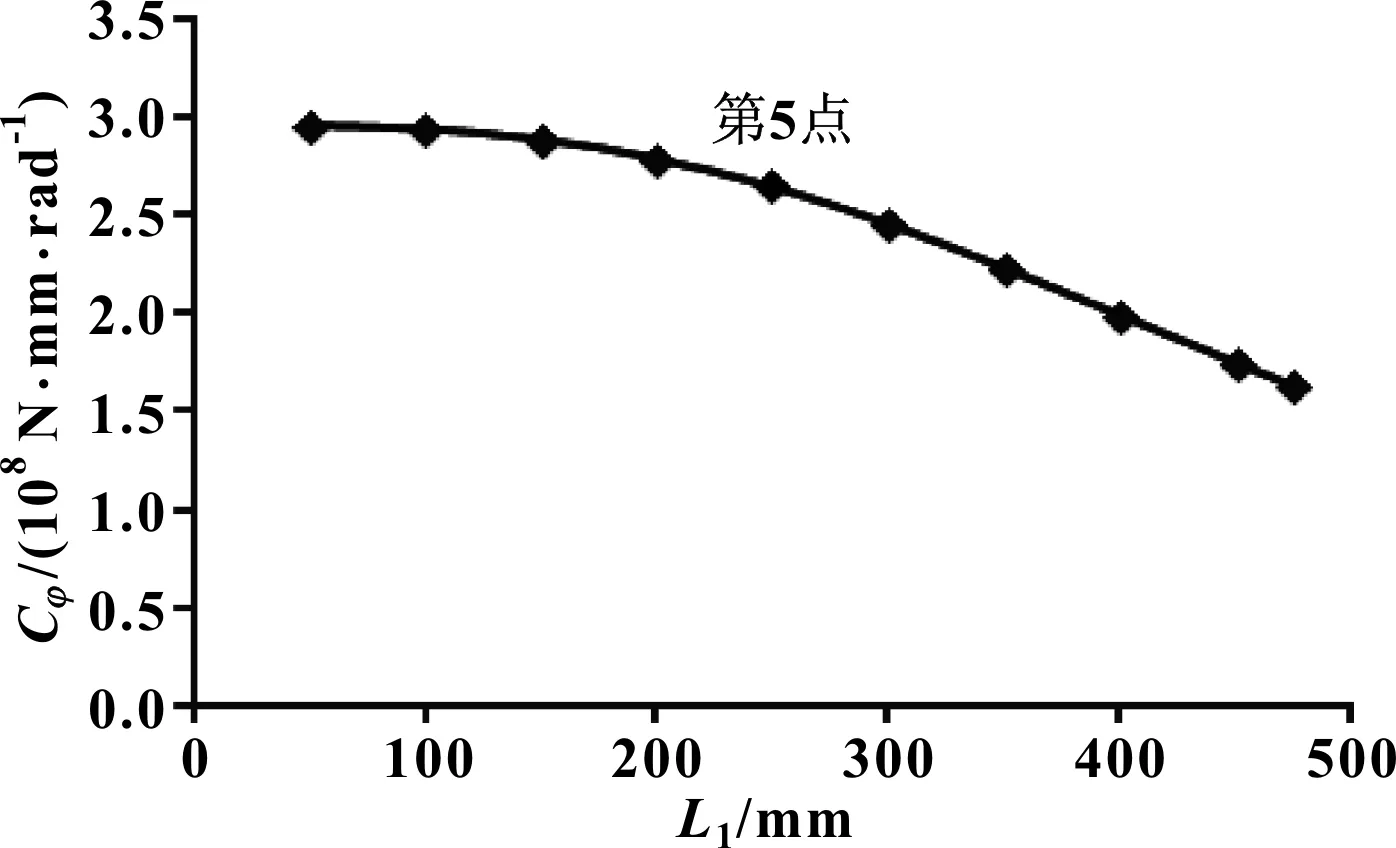
图2 尺寸参数L1对稳定杆侧倾刚度Cφ的影响曲线
分析图2可知:尺寸参数L1从第1点变化至第4点,稳定杆侧倾刚度降幅较平缓;第5点为影响曲线拐点,此时尺寸参数L1=L2=250 mm;L1从第5点变化至第10点,稳定杆侧倾刚度降幅呈线性函数变化。
其他参数不变的情况下,L1越小,稳定杆侧倾刚度越大。设计稳定杆时,需要考虑影响曲线的拐点(第5点),即L1<250 mm时,尺寸参数L1的变化对稳定杆侧倾刚度的影响较小。当空间布置紧张时,可充分利用L1影响曲线的拐点特性,调整整个稳定杆的设计方案。
2.2 尺寸参数L2的影响曲线
在其他参数不变的情况下,L2取点情况如表3所示。绘制尺寸参数L2对横向稳定杆侧倾刚度的影响曲线,如图3所示。

表3 L2取点表 mm
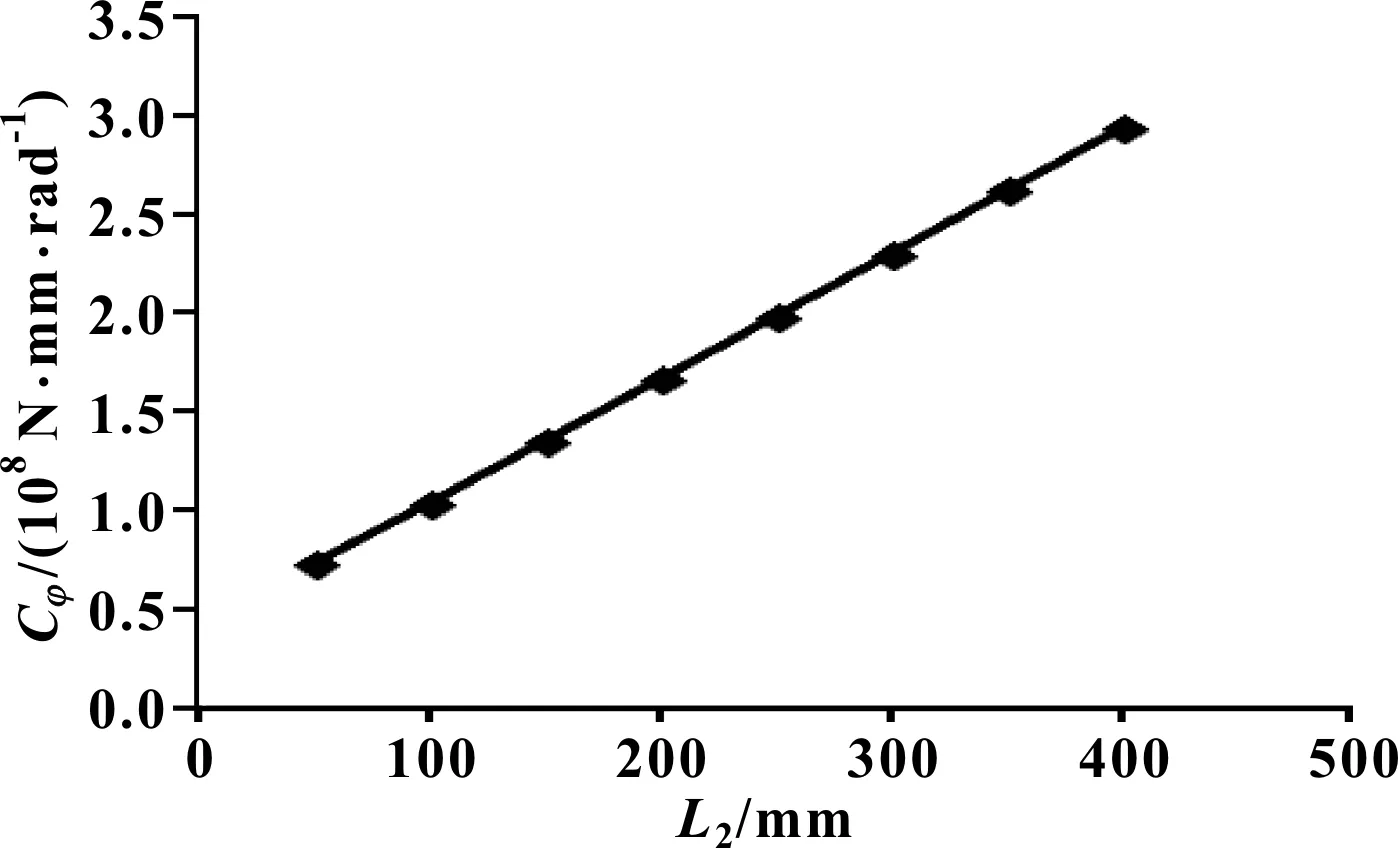
图3 尺寸参数L2对稳定杆侧倾刚度Cφ的影响曲线
分析图3可知:其他参数不变的情况下,横向稳定杆侧倾刚度Cφ与尺寸参数L2呈线性函数关系,L2变大,稳定杆侧倾刚度Cφ随之变大。在布置空间允许的情况下,可适当加大L2的尺寸,获取更优的稳定杆侧倾刚度。
2.3 尺寸参数L3的影响曲线
在其他参数不变的情况下,L3取点情况如表4所示。绘制尺寸参数L3对横向稳定杆侧倾刚度的影响曲线,如图4所示。
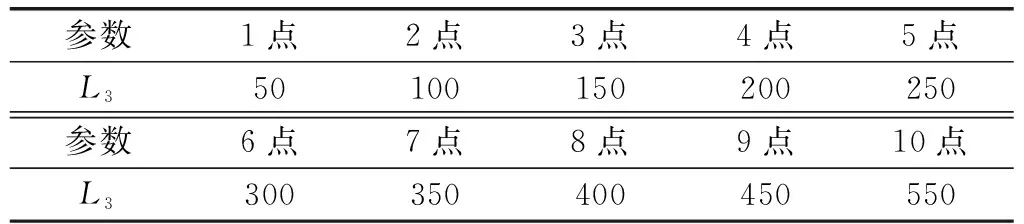
表4 L3取点表 mm
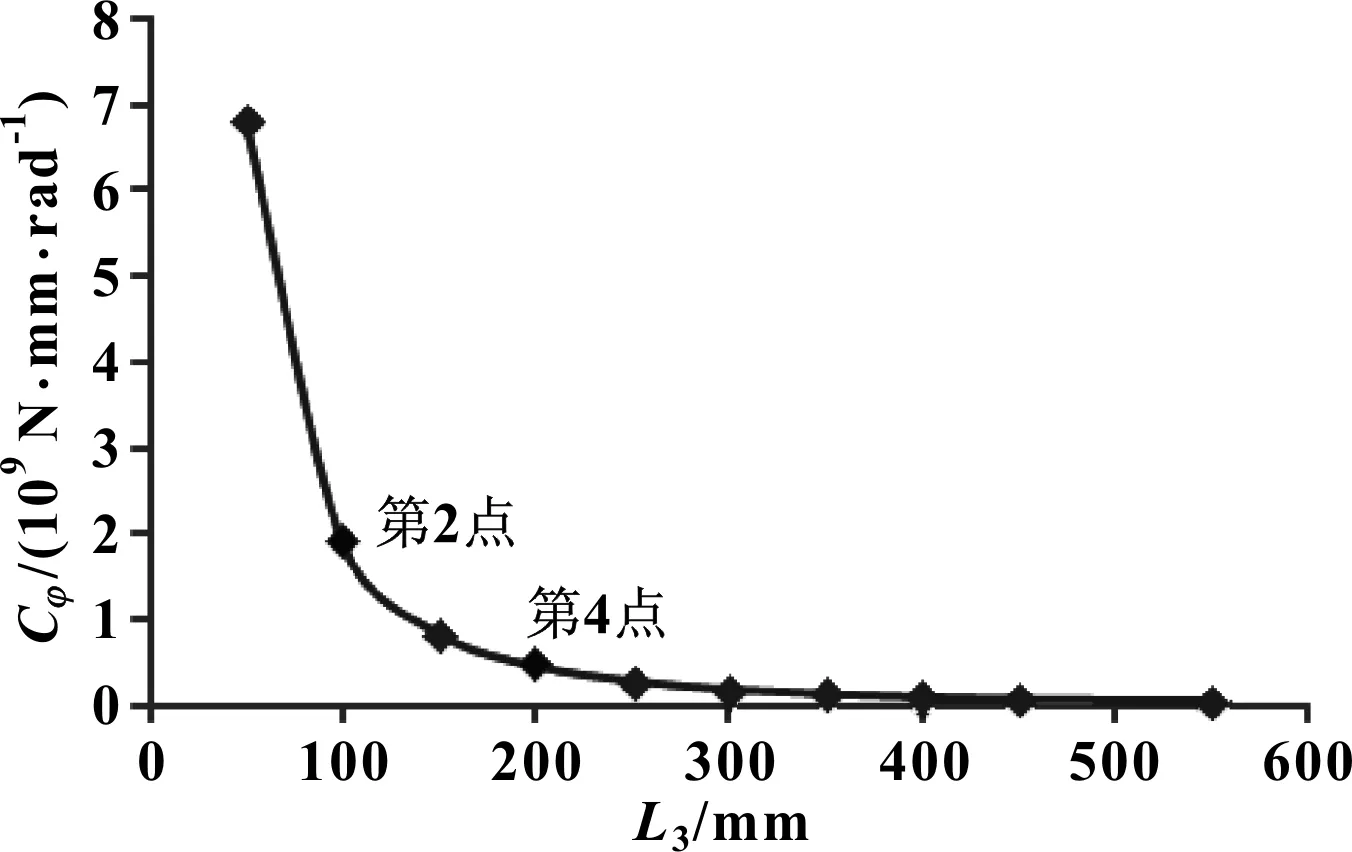
图4 尺寸参数L3对稳定杆侧倾刚度Cφ的影响曲线
分析图4可知:尺寸参数L3从第1点变化至第2点,稳定杆侧倾刚度降幅剧烈,降幅比例达到72.1%;第2点和第4点为影响曲线的两个拐点;L3从第4点变化至第10点,稳定杆侧倾刚度呈类似线性函数关系,降幅趋于平缓。
其他参数不变的情况下,L3越小,横向稳定杆侧倾刚度越大。设计稳定杆时,需要充分考虑尺寸参数L3的两个拐点(第2点和第4点)。当L3<100 mm时,能够获得较高的横向稳定杆侧倾刚度,此时需综合考虑空间布置和其他因素的影响;当L3>200 mm时,尺寸参数L3对横向稳定杆侧倾刚度的影响幅度逐渐减小。一般情况下,尽可能不要选择过大的L3,以免对稳定杆侧倾刚度造成不良影响。
2.4 尺寸参数R的影响曲线
在其他参数不变的情况下,R取点情况如表5所示。绘制尺寸参数R对横向稳定杆侧倾刚度的影响曲线,如图5所示。

表5 R取点表 mm
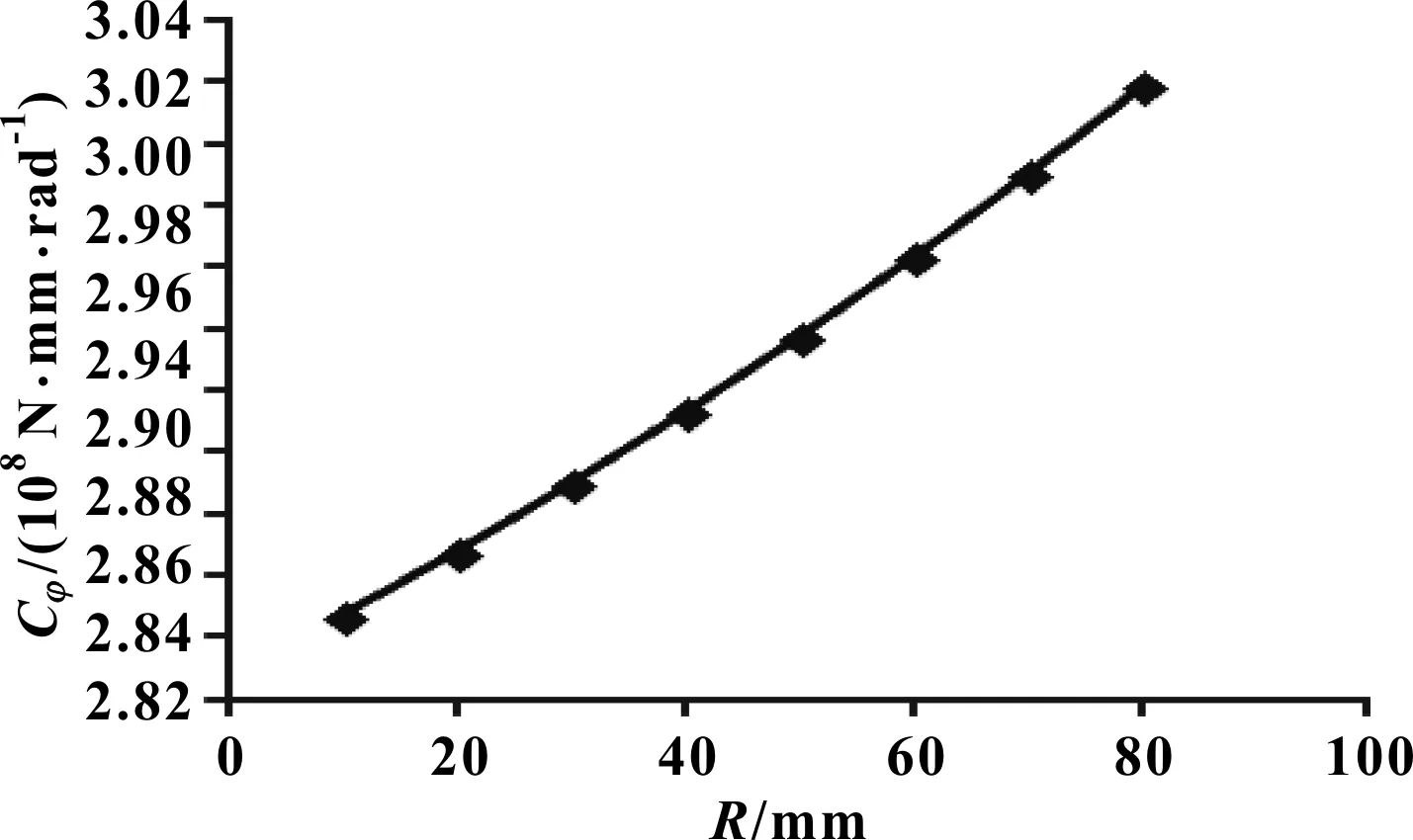
图5 尺寸参数R对稳定杆侧倾刚度Cφ的影响曲线
分析图5可知:其他参数不变的情况下,横向稳定杆侧倾刚度Cφ与尺寸参数R呈线性函数关系,R变大,稳定杆侧倾刚度Cφ随之变大。从图5还可以看出:尺寸参数R对稳定杆侧倾刚度的影响曲线的斜率为629 943 N·mm/(rad·mm)。条件允许情况下,可适当加大稳定杆折弯半径R,以获取更优的侧倾刚度。
2.5 尺寸参数d的影响曲线
在其他参数不变的情况下,d取点情况如表6所示。绘制尺寸参数d对横向稳定杆侧倾刚度的影响曲线,如图6所示。

表6 d取点表 mm
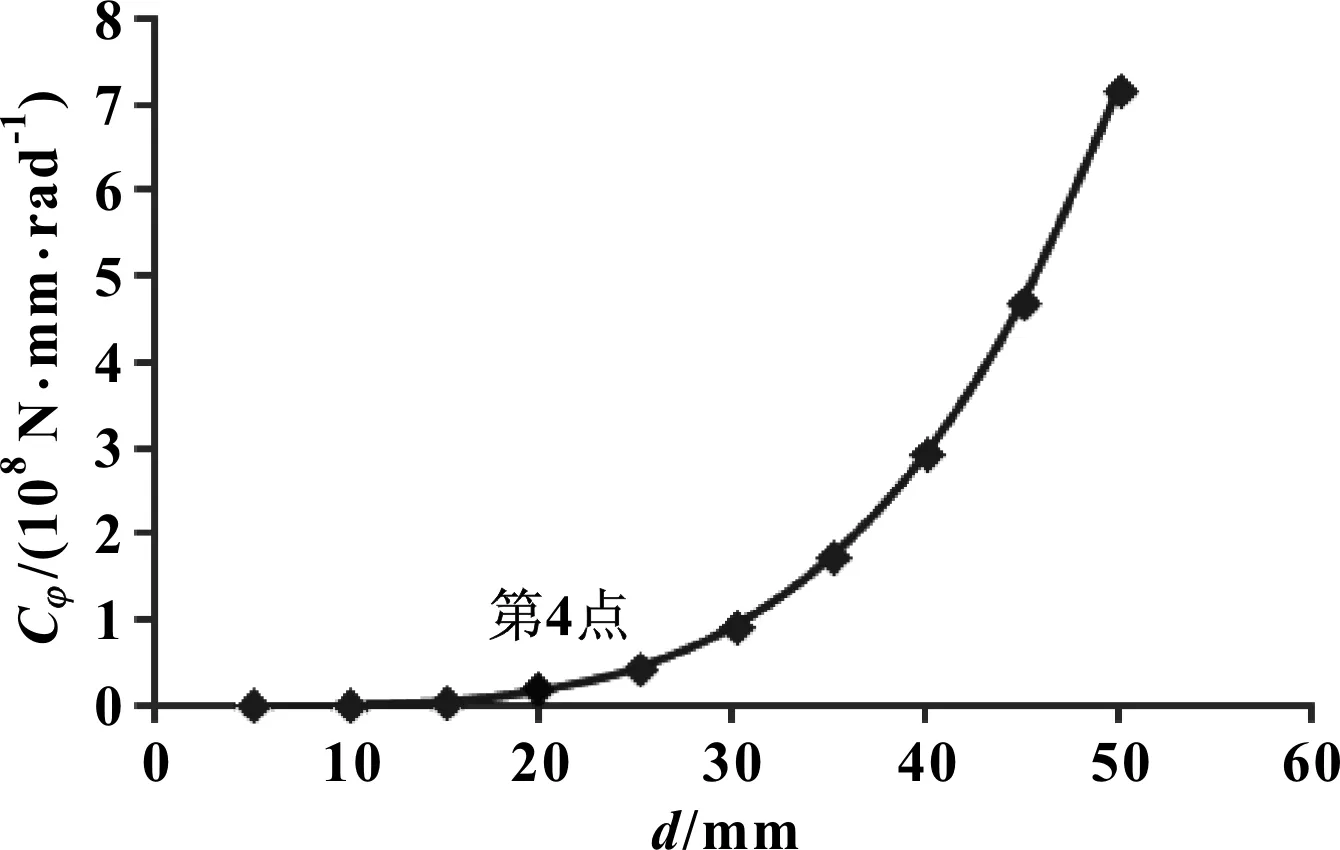
图6 尺寸参数d对稳定杆侧倾刚度Cφ的影响曲线
分析图6可知:尺寸参数d从第1点变化至第4点,稳定杆侧倾刚度变化幅度较平缓;第4点为影响曲线的拐点,从第4点开始,稳定杆侧刚度随尺寸参数d的变化幅度逐渐剧烈,曲线呈幂函数趋势变化,与公式(1)相符合。在设计稳定杆时,可适当加大稳定杆外径d的尺寸,获取更优的稳定杆侧倾刚度,同时,需要综合考虑轻量化的需求。
3 截面尺寸参数
3.1 空心稳定杆外径d′的影响曲线
随着整车及零部件轻量化的需求不断发展,市场上出现越来越多的空心横向稳定杆。除了能够降质量,实现轻量化的目标,选择得当,空心稳定杆还能够得到比实心稳定杆更优的侧倾刚度,在设计上实现双赢。
在其他参数不变的情况下,取内径D=φ20 mm,保持不变。空心稳定杆外径d′的取点情况如表7所示。绘制空心稳定杆外径d′对横向稳定杆侧倾刚度的影响曲线,如图7所示。
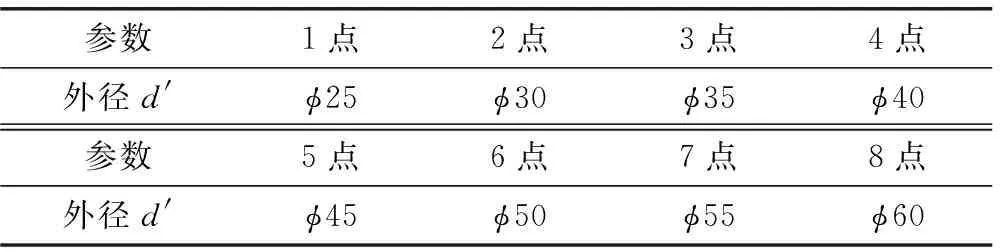
表7 空心稳定杆外径d′取点表 mm
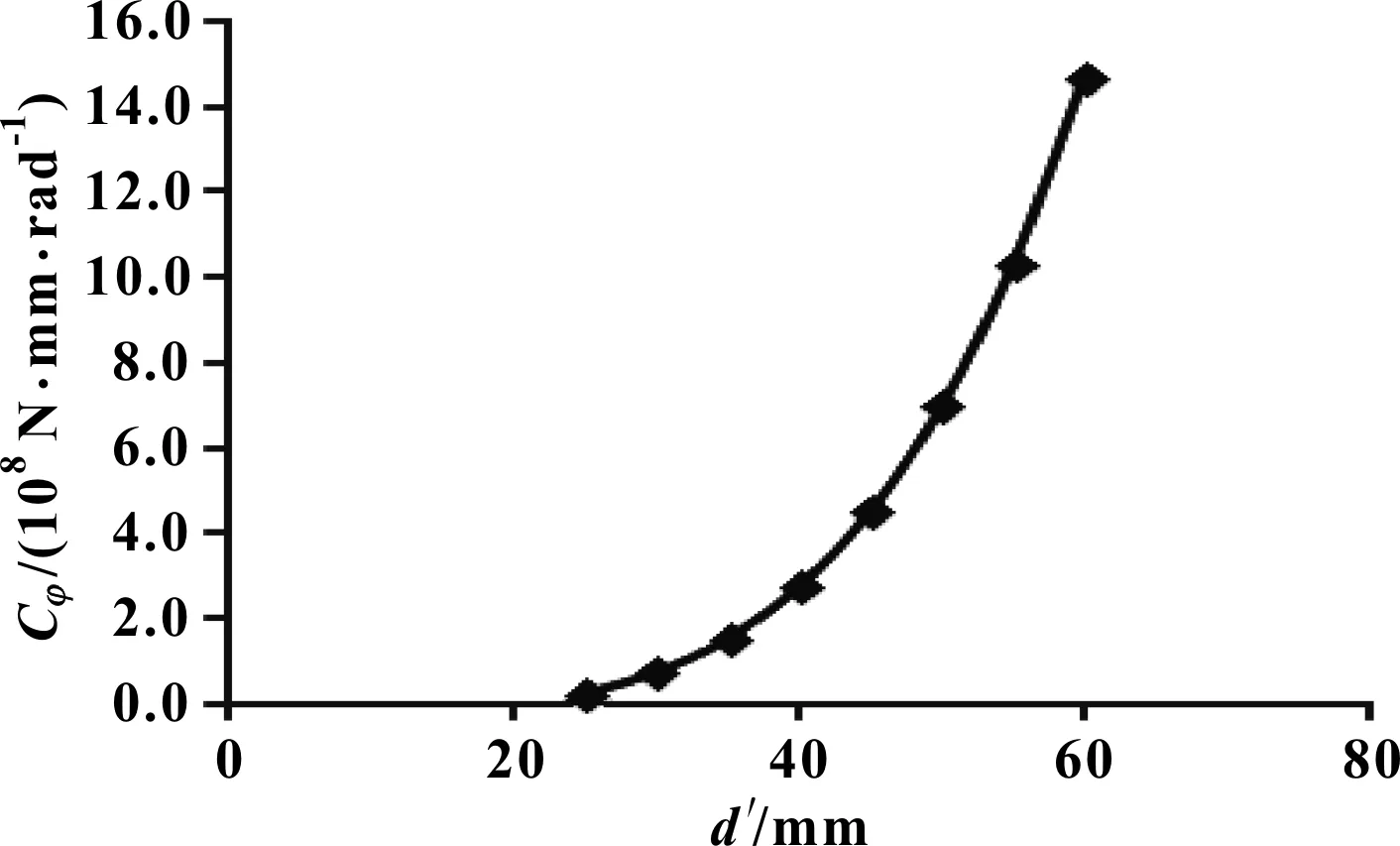
图7 空心稳定杆外径d′对稳定杆侧倾刚度Cφ的影响曲线
分析图7可知:在其他尺寸参数均保持不变的情况下,空心稳定杆的侧倾刚度与其外径d′的变化趋势与图6类似,随着空心稳定杆外径d′的增大,空心稳定杆的侧倾刚度呈幂函数增长。当外径d′与内径D的差值逐渐变大,空心稳定杆的侧倾刚度涨幅逐渐加剧。
3.2 空心稳定杆内径D的影响曲线
在其他尺寸参数不变的情况下,取外径d′=φ40 mm,保持不变。空心稳定杆内径D的取点情况如表8所示。绘制空心稳定杆内径D对横向稳定杆侧倾刚度的影响曲线,如图8所示。
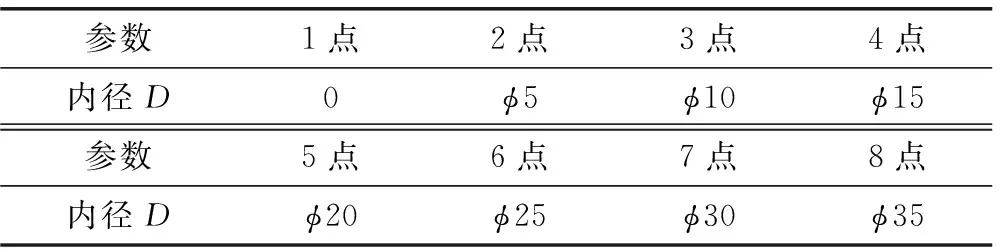
表8 空心稳定杆内径D取点表 mm

图8 空心稳定杆内径D对稳定杆侧倾刚度Cφ的影响曲线
分析图8可知:空心稳定杆的内径D从第1点变化至第4点,其刚度降幅非常平缓,第4点为影响曲线的一个拐点;从第4点开始,随着空心稳定杆内径D增大,稳定杆侧倾刚度降幅逐渐增大。
在其他参数不变的情况下,由图8可知:空心稳定杆的内径D不是越小越好。当保证空心稳定杆外径d′=φ40 mm不变,内径D取小于φ15 mm的任意值时,对稳定杆侧倾刚度的影响甚微。因此,综合考虑横向稳定杆轻量化指标,在设计时,可以适当选择空心稳定杆结构。根据图8所示的影响曲线,选择内径D≤φ15 mm的空心稳定杆时,能够得到与实心稳定杆相当的侧倾刚度,同时,实现轻量化目标约达14%。
3.3 质量相同情况下实心杆与空心杆的比较分析
在稳定杆其他尺寸参数不变的情况下,稳定杆的截面积相等便可实现质量相等。在保证实心稳定杆与空心稳定杆截面积相等的情况下,实心稳定杆直径d与空心稳定杆的内径D和外径d′的取点情况如表9所示。绘制两种横向稳定杆侧倾刚度随截面积的变化曲线,如图9所示。
分析图9可知:相同质量(截面积)的情况下,空心稳定杆的侧倾刚度比实心稳定杆的侧倾刚度普遍偏大。随着截面积变大,空心稳定杆与实心稳定杆的侧倾刚度的差值逐渐变大。因此,在保证相同的稳定杆总成侧倾刚度的情况下,空心稳定杆的质量更轻,能够更好地实现轻量化。
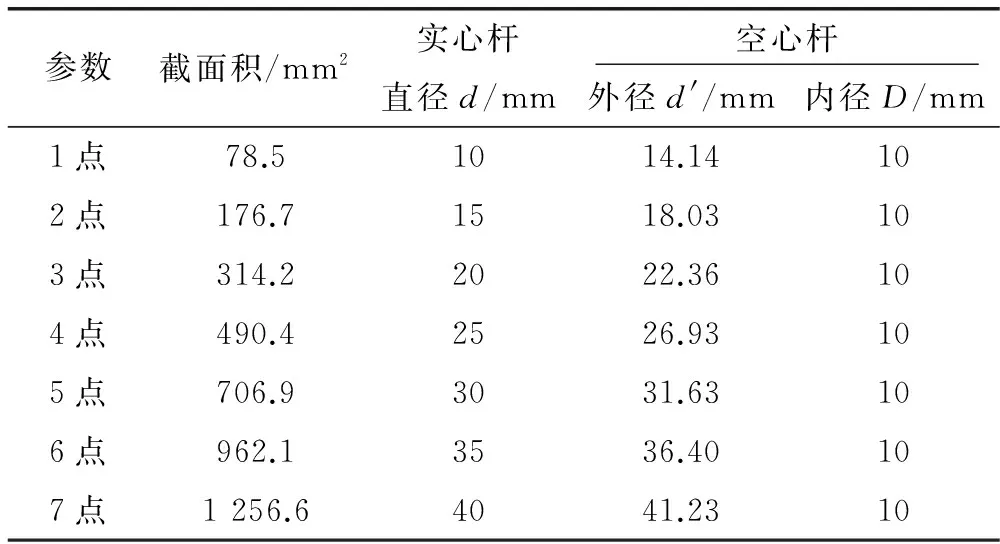
表9 相同质量(截面积)情况下,稳定杆直径取点表
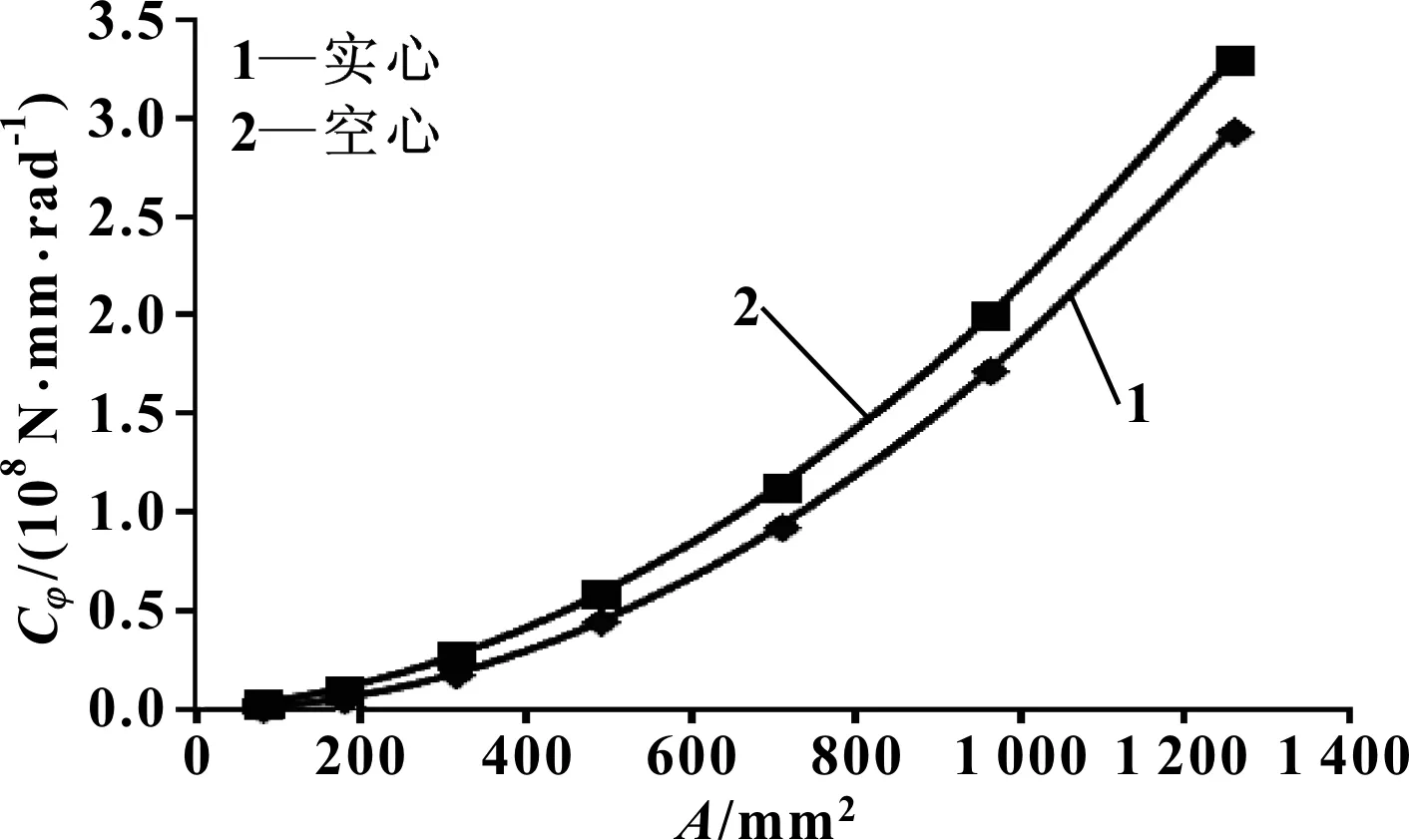
图9 相同质量(截面积)情况下,实心杆与
4 形状尺寸参数
4.1 梯形横向稳定杆侧倾刚度理论计算公式
近年来,商用车用横向稳定杆逐渐从单一的直角形向梯形或者复杂形状发展。梯形稳定杆由于性能良好、方便布置和制造,逐渐得到应用。
梯形稳定杆侧倾刚度理论计算简图如图10所示。
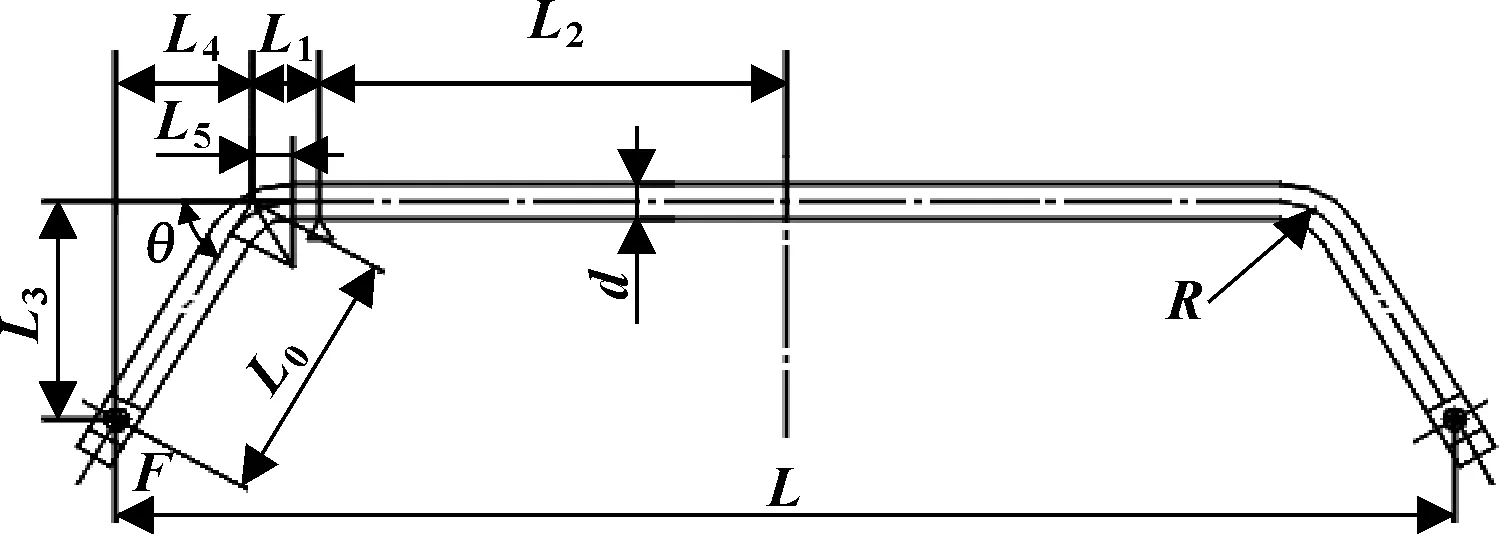
图10 梯形横向稳定杆示意图
公式(1)是横向稳定杆侧倾刚度理论计算的通用公式,对于梯形横向稳定杆依然适用,但是公式中的P和U有所不同。依据梯形横向稳定杆自身的结构特点,根据能量原理,推导出公式(1)中,适用于梯形横向稳定杆侧倾刚度的P和U的公式,如下所示:
(4)
(5)
(6)
4.2 梯形稳定杆夹角θ的影响曲线
在其他尺寸参数不变的情况下(如表1),夹角θ取点情况如表10所示。绘制夹角θ对梯形横向稳定杆侧倾刚度的影响曲线,如图11所示。
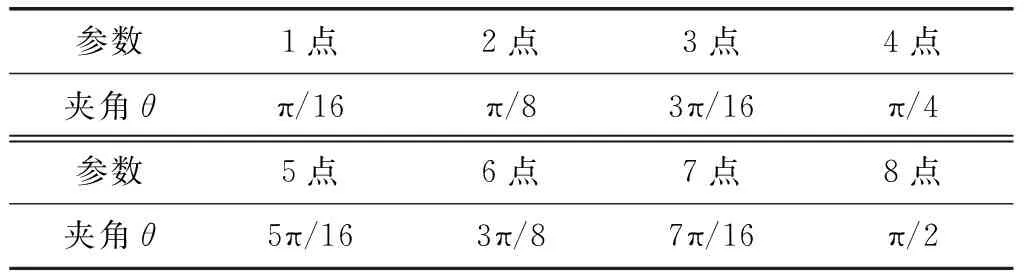
表10 夹角θ取点表 rad
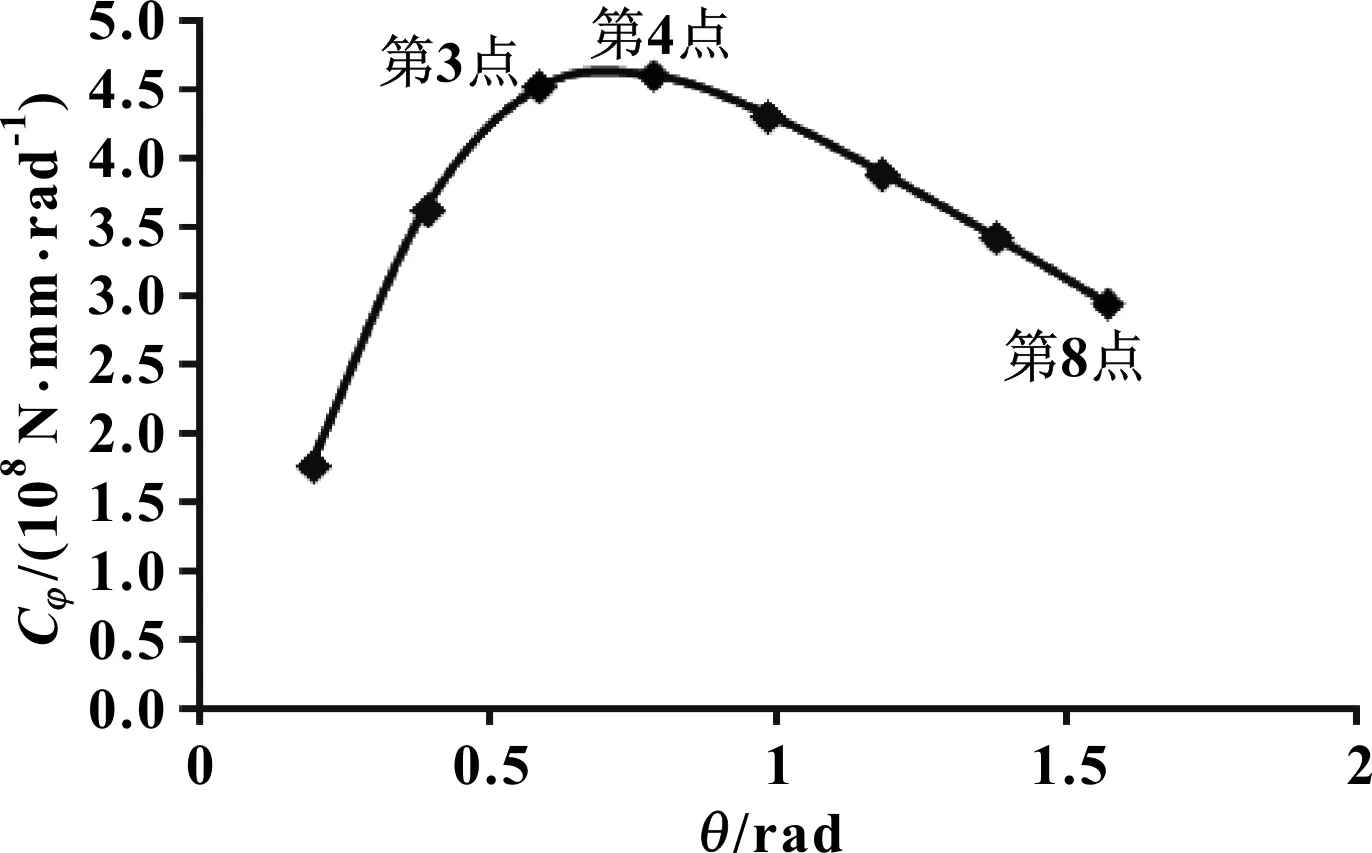
图11 夹角θ对梯形横向稳定杆侧倾刚度Cφ的影响曲线
分析图11可知:第4点(θ=π/4)是一个峰值点;夹角θ在第3点(θ=3π/16)与第4点(θ=π/4)间取值时,梯形稳定杆侧倾刚度变化较平缓,是梯形横向稳定杆夹角θ取值的合适区间;从第4点(θ=π/4)至第8点(θ=π/2),随着夹角θ增大,梯形横向稳定杆的侧倾刚度线性减小,直至第8点(θ=π/2),此时稳定杆为直角形状。由此可见:从第2点开始,即当π/8<θ<π/2时,梯形横向稳定杆侧倾刚度均比直角形横向稳定杆(θ=π/2)侧倾刚度大。因此,在设计横向稳定杆时,综合考虑其他因素,可适当选择梯形横向稳定杆,以便获取更优的侧倾刚度。选择梯形稳定杆时,以夹角θ趋于π/4为宜。
5 验证
目前国内、外市场上,商用车用横向稳定杆的形状大体分为直角形、类直角形、梯形或类梯形。截面积形式以实心为主,偶尔出现空心稳定杆。文中列举国内、外不同厂家的横向稳定杆的基本尺寸参数、截面尺寸参数和形状尺寸参数,进行对比分析,便可对文中所绘制的尺寸参数影响曲线进行实际验证。
对比分析表11可知:国内厂家B的尺寸参数L1取值明显比其他3家偏大。根据图2可知,单从稳定杆侧倾刚度分析,厂家B选择的尺寸参数L1不甚合理,其他3家选择的L1在合理区域。
国内、外4个厂家对于尺寸参数L2的选择一致性较好,与整车布置空间有关。
国内、外厂家对于尺寸参数L3的选择存在较大分歧。根据图4可知:L3越大,稳定杆侧倾刚度会越小,影响曲线的拐点为L3=200 mm。由此可知,国外厂家选择的尺寸参数L3较合理。一般情况下,尽可能不要选择过大的L3,以免对稳定杆侧倾刚度造成不良影响。
由表11可知:目前市场上,以直角形实心横向稳定杆为主流形式。由于市场对轻量化的关注度不断提升,空心稳定杆已逐渐出现,但并未被广泛采用。
综上所述:国外两个厂家横向稳定杆的尺寸参数基本遵循尺寸参数影响曲线的变化规律进行选择,尺寸参数基本位于影响曲线的合理区域,参数一致性较好。国内两个厂家横向稳定杆部分尺寸参数离散性较大,根据尺寸参数影响曲线,还有进一步优化的空间。通过4个国内、外横向稳定杆实际尺寸参数的对比分析,验证了文中绘制的稳定杆尺寸参数影响曲线的正确性。同时,尺寸参数影响曲线对于稳定杆设计和优化都有较直观和精确的指导意义。
6 结论
通过对横向稳定杆的基本尺寸参数、截面尺寸参数和形状尺寸参数的分析,从理论计算入手,得出各种尺寸参数对横向稳定杆侧倾刚度的影响曲线。文中得到以下几点结论:
(1)基本尺寸参数(L1、L2、L3、R和d)对稳定杆侧倾刚度的影响趋势和影响程度各不相同。文中绘制的基本尺寸参数对稳定杆侧倾刚度的影响曲线,能够直观、精确地判断各基本尺寸参数对稳定杆侧倾刚度的影响情况。在稳定杆设计初期,可方便、快捷、精准地确定各基本尺寸参数;
(2)空心稳定杆与实心稳定杆相比较,既能够得到较优的侧倾刚度,还能够实现轻量化的目标,是稳定杆设计中的一个双赢的方案;
(3)梯形稳定杆相较于传统直角形稳定杆有更优的侧倾刚度。当梯形稳定杆的夹角θ趋近π/4时,可获得最优的侧倾刚度;
(4)空心稳定杆及梯形稳定杆是横向稳定杆发展的趋势,设计时可根据文中绘制的不同参数的影响曲线,确定合适的尺寸参数;
(5)结合国内、外4个厂家横向稳定杆尺寸参数,验证了文中推导的尺寸参数影响曲线的正确性及其指导意义。
【1】曾林.车用稳定杆及其发展前景[J].弹簧工程,1993(2):2-8.
【2】黄康,仰荣德.基于ANSYS的汽车横向稳定杆疲劳分析[J].机械设计,2008,25(12):66-68. HUANG K,YANG R D.Fatigue Analysis on the Automobile Transverse Stability Rod Based on ANSYS[J].Journal of Machine Design,2008,25(12):66-68.
【3】刘惟信.汽车设计[M].北京:清华大学出版社,2001:510-512.
【4】日本自动车技术会.汽车工程手册5 底盘设计篇[M].中国汽车工程学会组,译.北京:北京理工大学出版社,2010:31-33.
Analysis and Verification of the Dimension Parameter Impact on the Roll Stiffness of the Stabilizer Bar
WANG Xiaolian, ZHANG Xuebo
(Research & Development Center,China FAW Co., Ltd.,Changchun Jilin 130011,China)
In the stabilizer bar design process, the choice of the dimension parameter impacts the roll stiffness of the stabilizer bar directly. The roll stiffness of the stabilizer bar is affected by many dimension parameters. The calculating formula is complex, it is difficult to choose the dimension parameter intuitively in initial stage design. Based on theoretical calculation, the influence curves which single parameter impacted on the roll stiffness of the stabilizer bar were drawn. The curves could be used to judge the influence degree which different parameters impacted on the roll stiffness of the stabilizer bar. Combining the actual dimension parameters of domestic and foreign products, through comparative analysis, the correctness of the influence curves was verified. The problem that is difficult to choose and optimize dimension parameters accurately in initial design stage is solved.
Stabilizer bar; Roll stiffness; Dimension parameter; Influence curve
2017-01-11
王晓莲(1984—),女,硕士,工程师,研究方向为悬架系统设计与开发、整车可靠性开发及对标等。E-mail:wangxiaolian@rdc.faw.com.cn。
10.19466/j.cnki.1674-1986.2017.05.006
U463.33
A
1674-1986(2017)05-028-06

