自动化立体仓库中智能AGV群体的静态路径规划与动态避障决策研究

房殿军，周 涛

（同济大学 中德学院，上海 201804）

自动化立体仓库中智能AGV群体的静态路径规划与动态避障决策研究

房殿军，周 涛

（同济大学 中德学院，上海 201804）

针对自动化立体仓库出入库搬运作业区域自动化水平低的现状，结合智能物流的发展趋势，阐述以智能AGV群体替代叉车作业进行托盘搬运的工作模式，并对其静态路径规划与动态避障决策进行了研究。以此工作模式下的AGV为特定对象，在A-star算法的基础上考虑了时间因子的影响，进行了路径规划的算法设计；同时根据栅格图下AGV碰撞的路径特点，系统地阐述了AGV群体的碰撞类型及避障策略，并对智能AGV群体的路径规划、动态避障和路径再规划进行了算例分析。

智能AGV群体；路径规划；碰撞类型；动态避障

1 引言

近年来，电子商务发展非常迅速。相对于传统零售行业，电子商务企业的物流作业不仅工作量巨大，还对时效性和准确性提出了非常严苛的要求。与此同时，传感器技术、RFID技术、嵌入式系统技术等物联网技术的发展，为智能物流提供了强有力的支撑。智能化物流系统是解决目前电商物流问题切实可行的方案，也是未来的发展趋势。

自动化立体仓库（AS/RS）作为智能物流仓储系统的核心组成部分，被广泛应用于各行各业。自动化立体仓库的巷道堆垛机与立体货架可高效且准确地实现托盘在货架上的存取。可是在自动化立体仓库的出入库搬运作业区域中，往往需要人驾驶叉车进行托盘的搬运。这不仅影响了整个物流仓储系统的自动化程度，也易导致错误作业甚至无效作业，降低物流系统整体的效率。

随着物联网技术的发展，AGV作为柔性单元，可替代人工操作叉车进行托盘搬运工作，从而使得整个仓储系统自动、智能的运转，并可通过AGV数量的增减及时响应作业量的波动。基于物联网技术的自动化立体仓库示意图如图1所示，在出入库区域，使用多个AGV进行托盘搬运作业。

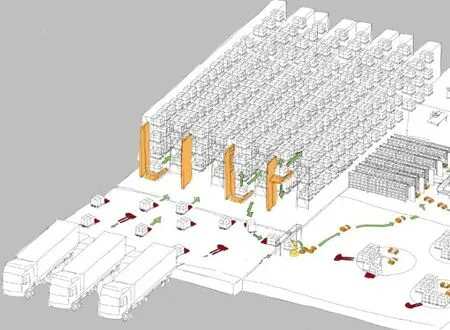
图1 基于物联网技术的立体仓库示意图[1]

区别于传统的多AGV系统，智能AGV群体更强调“智能群体”的理念。“智能”意味着：AGV可通过传感器获取环境信息，通过RFID技术与其他设备（其他AGV、堆垛机、位置标签等）进行信息交互，最后AGV自身通过数据运算做出路径和避障等决策。群体则代表着：系统中每辆AGV都是平等独立的个体，每辆AGV分别进行运算，分别对自身的运动进行决策，而不依托于其他AGV或中央控制器的指令。在物联网技术的支持下，智能AGV群体进行搬运工作是未来的趋势。

传统的AGV系统大多通过上层的中央控制器进行多AGV的调度，如：基于时间窗的多AGV路径规划[2]，通过蚁群算法求多AGV系统总路径的全局最优解[3]，基于有向图的AGV路径规划和系统任务调度的AGV管理系统[4]。此种多AGV调度系统在路径规划时直接考虑了避障，综合已知的任务序列，规划所有AGV的路径，可得整个系统的最优解。可是这种模式比较适用于小型的AGV系统，如果AGV数量不断增多，那么中央控制器的计算量将成指数增长，运算耗时长，导致AGV的实时规划和避障难以实现。近年来随着智能物流的发展，众多学者纷纷将目光从集中式控制AGV系统转向分布式AGV系统，如：单车使用改进的Dijkstra算法规划路径，基于冲突协商策略实现多AGV自主控制[5]。分布式AGV系统将冗杂的集中式计算转化为各个AGV的分布式计算，响应速度快，具有更高的柔性和鲁棒性，更适用于大型电商等订单多且难预测的情况。

在目前分布式AGV系统的研究中，大多以路径长度作为评判指标进行路径规划，未考虑AGV转向时间以及转向前后加减速阶段时间因素的影响。而在实际应用中，AGV在两点间选取不同的路径所需要的转向及加减速次数是不一样的。而频繁的转向与加减速，不仅仅影响了AGV的作业时间，同时增加了AGV系统运作的能耗。而且，复杂动作对于AGV的机构也会造成一定的损耗，导致AGV后期的维护保养成本增高。因此在实际应用中，距离最短的路径并不是最优的，而是需综合转向次数，考虑时间因素的影响，进行路径规划和避障决策。

本文针对实际自动化立体仓库的运作情况，基于时间因子来设计立体仓库中出入库搬运区域的AGV路径规划算法，同时针对此对象，定义AGV群体的动态避障决策机制，框架如图2所示。

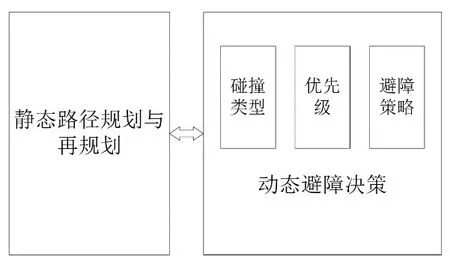
图2 本文框架图

以最短运行时间作为评判指标，设计AGV路径全局规划算法，实现路径的静态规划与再规划。在AGV运动过程中，通过碰撞类型判定、优先级排序以及避障策略选取来决策AGV群体的动态避障，并在避障的基础上进行路径再规划。针对时间因子的影响，本文系统地阐述了此对象中AGV群体的碰撞类型和避障策略，并进行了算例验证。

2 问题描述

本文所考虑的是自动化立体仓库出入库托盘搬运作业区域AGV群体运动规则的问题。某立体仓库作业区域为矩形，长22.5m，宽15m，作业对象为标准化托盘，作业主体为AGV。故而，本文采用栅格图法搭建地图模型。

常用托盘尺寸为：1.1m×1.1m，0.8m×1.2m，1m×1.2m。不同生产厂商AGV外观尺寸各不相同，且AGV外观尺寸的会根据额定载荷变化，额定载荷越高，尺寸就会设计得越大。通常长为0.9m-1.3m，宽为0.6m-1.0m，高为0.2m-0.4m。综合考虑运行时的干涉以及作业区域的空间利用率，设定栅格尺寸为1.5m×1.5m，栅格尺寸略大于AGV与托盘尺寸。

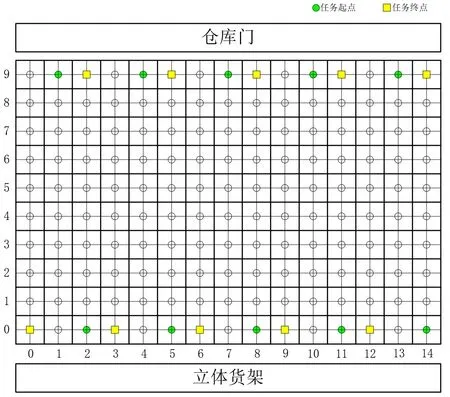
图3 某仓库托盘搬运区域栅格图

图3为某立体仓库托盘搬运作业区域的栅格地图模型。粗实线为自动立体仓库各区域边界以及栅格边界，每个栅格中心点为AGV小车在栅格内的位置点，也是整个电子地图的坐标点，细实线为各中心点的连线，也即是AGV的实际行走路径。左下角第一个栅格坐标定为（0,0），整个地图坐标从（0,0）到（14,9）。

仓库共设5扇门，门宽3m左右，门外停放车装卸货物。立体货架共设5条巷道，对应图2中横坐标1，4，7，10，13的位置。在栅格和立体货架连接处，巷道两侧分别设有出入库工作台，以便堆垛机存取托盘。结合上述特点设定搬运任务起点与搬运任务终点（如图3所示）。门侧任务起点连接卡车卸货区，任务终点连接卡车装货区；货架侧的任务起点连接货架出库台，任务终点连接货架入库台。AGV小车在立体货架和仓库门间双向行驶完成出入库搬运作业。本文将从静态路径规划以及动态避障两个角度展开，逻辑流程如图4所示。

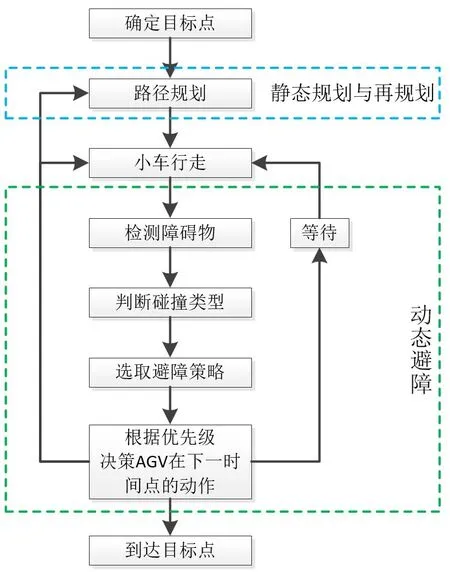
图4 逻辑流程图

根据现有主流物流设备的额定参数，结合本文研究对象的特点，考虑到模型的可实现性与现实意义，现对本文模型作如下假设。

（1）AGV小车具有4个可移动方向，只能在不为对角的两相邻栅格间移动；

（2）为了简化模型，将AGV加减速时间进行折算，小车在相邻栅格间的移动时间需1s；

（3）考虑AGV的转向影响，设置AGV小车转向方式为原地自旋，且转向需要固定时间为1s；

（4）鉴于目前的电池技术，AGV小车续航可达24h，故在本文中不考虑充电问题；

（5）障碍检测频率为1次/s；

（6）障碍检测半径为6m；

（7）AGV小车抬起和放下托盘的工作时间为1s；

（8）安全距离为1.5m。当AGV小车检测到与另外小车距离（两AGV中心点的距离）小于1.5m（一个栅格）时，此AGV急停1s。

3 基于时间因子的AGV静态路径规划

AGV路径规划问题是典型的车辆路径问题（Vehicle Routing Problem，VRP）。VRP问题一般可定义为：对于一系列装货点和（或）卸货点，组织合适的行车线路，使载货车辆有序地通过节点，在满足一定的约束条件（如货物需求量、发送量、交发货时间、车辆容量限制、行驶里程限制、时间限制等）下，达到一定的目标（如路程最短、费时最少、时间尽量少、使用车辆数量尽量少等）[6]。在常规栅格图路径静态规划中，通常假设AGV速度恒定，将路程最短与时间最短划等号，忽略了AGV转向与加减速所导致的时间影响。本文基于时间因子进行AGV静态路径规划，实现了路径规划目标由最短路径向最短时间的转变。

3.1 基于时间因子的A-star算法设计

3.1.1 A-star算法流程。当AGV接收到一个任务，则此次任务的初始结点和目标结点已给定，属于启发式搜索的解决范畴[7]。基于栅格地图的启发式搜索算法中，A-star算法具有计算量小、搜索空间小等特征。它在搜索下一节点时，只搜索其相邻的栅格，而不是盲目搜索。

A-star算法的代价函数为：

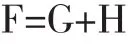
G表示从初始结点到当前结点的代价，H表示当前结点到目标结点的代价估值。F则为总移动代价。每次都选F值最小的结点进行搜索，就可以得到一条到终点消耗最少的路径。

在A-star算法中还有两个很重要的概念：开放列表（open list）和关闭列表（close list）。列表中存放着路径结点组成的数组。开放列表记录了路径规划过程中待搜索结点列表，即可能要走的区域；关闭列表记录了不需再次搜索的结点列表，即不会再考虑的区域，算法具体流程如图5所示。

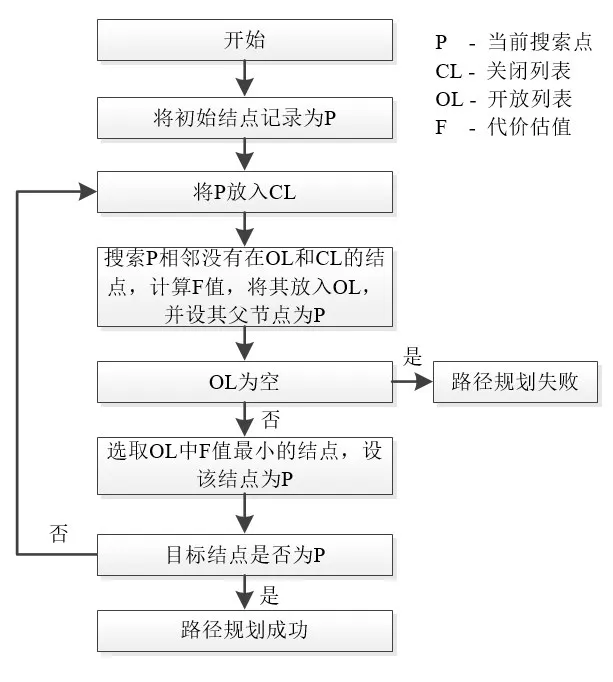
图5 A-star算法流程图

步骤1：将初始结点记录为当前搜索点P；

步骤2：将当前点P放入关闭列表；

步骤3：搜索点P所有相邻结点，假如某结点没有在两列表里，则计算出该结点的F值，并设其父节点为P，然后将其放入开放列表；

步骤4：判断开放列表是否已经为空，若是，则说明在达到目标结点前已经找完了所有可能的路径结点，路径规划失败，算法结束；否则继续；

步骤5：从开放列表取出任意一个F值最小的结点，将该结点设为当前结点P，返回步骤3；

步骤6：当目标结点进入开放列表，算法结束。

此时由目标结点开始逐级追溯父结点，直至初始结点，此时各结点相连即为路径。

3.1.2 基于时间因子的算法设计。A-star算法是种启发式搜索算法，那么代价函数中G与H的准确性决定了路径规划结果的有效性。很显然通常选取的距离评判指标（曼哈顿距离和欧式距离）都不适用于本文的研究对象。考虑到AGV的转弯时间以及行驶距离与行驶时间的关系。设定行驶最短时间为路径规划的评判指标，并基于时间因子进行算法设计。

设初始结点为(x1,y1)，AGV在初始结点方向为(a1,b1)，当前结点坐标为(x2,y2)，当前结点相对于父结点方向为(a2,b2)，目标结点为(x3,y3)，则：

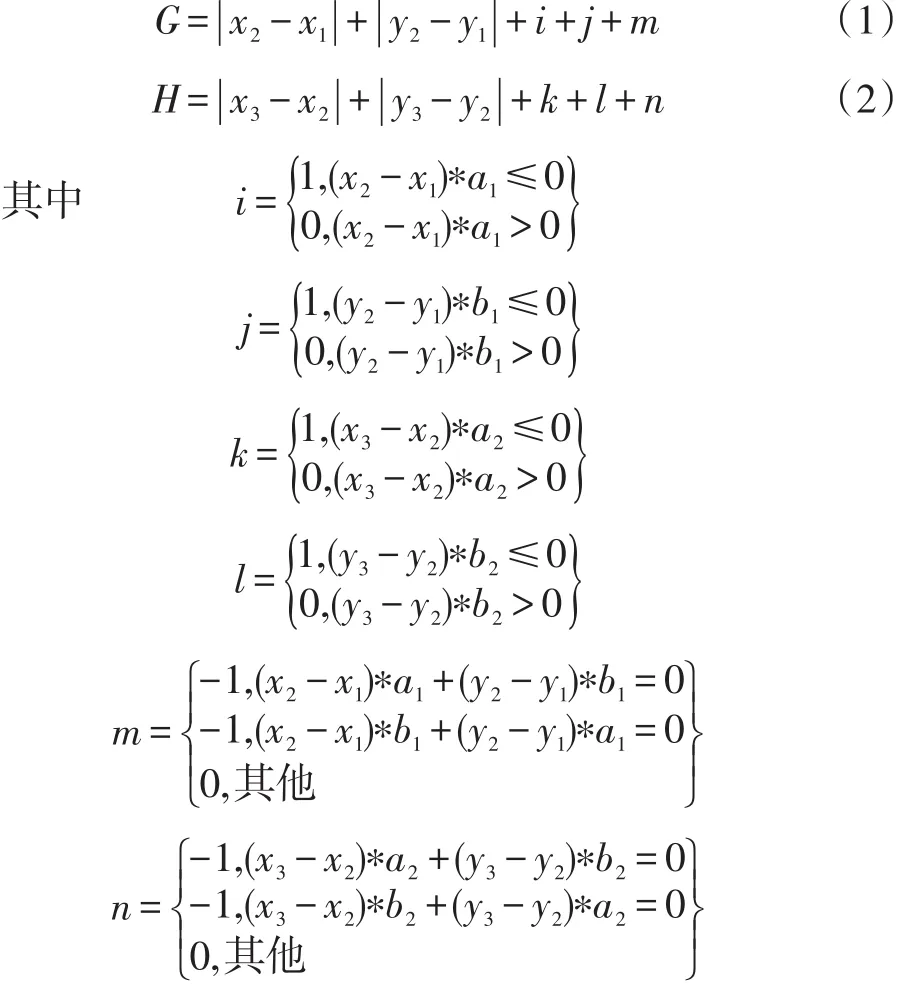
|x2-x1|+|y2-y1|和|x3-x2|+|y3-y2|，分别为当前结点与初始结点和目标结点曼哈顿距离。

i与k变量是判别x轴方向是否需要转向，代表转向所需的时间。

j与l变量是判别y轴方向是否需要转向，代表转向所需的时间。

m与n变量则是为了补偿直线行走的估值误差。

因为引入了时间因子，在搜索计算F值时需要当前结点相对于父结点方向。在不同搜索路径的情况下，当前结点F值会因不同的父结点而不同。针对本文基于时间因子的A-star算法，在搜索时不但需要搜索不在关闭列表与开放列表的结点，同时也需要搜索当前结点周围开放列表内的结点，再次计算总代价值F，并更新开放列表。基于时间因子的A-star算法流程图如图6所示。

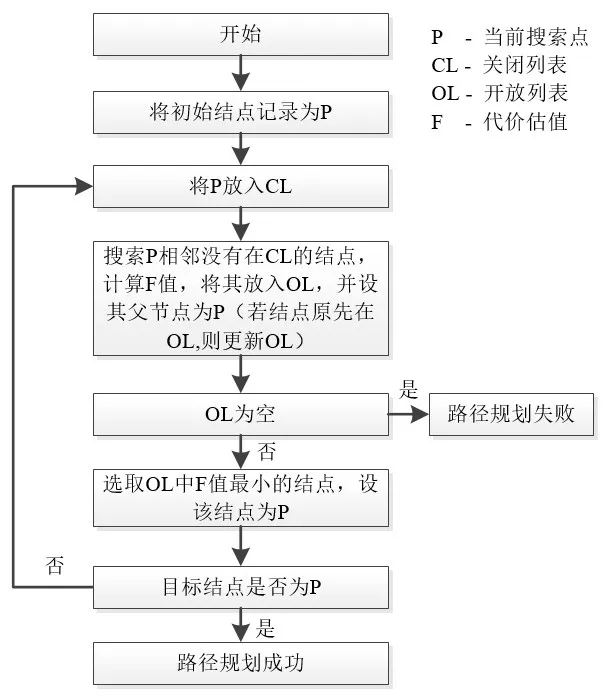
图6 基于时间因子的A-star算法流程

3.2 静态路径规划算例分析

给定初始结点、初始方向和目标节点进行规划，是静态路径规划问题最理想的情况，此种情况搜索范围最小，路径规划速度最快。然而在实际的生产实践中，作业区域可能会有很多物理约束，比如在地图中某些区域会放置固定设备，AGV在行驶过程中突然死机等情况。在A-star算法中，考虑实际物理约束时，只需要将约束点在路径规划阶段放入关闭列表，那么在规划时，就不再考虑通过约束结点的路径，从而达到避开静态障碍物的目的。在动态避障后的路径再规划阶段，只需要将碰撞结点放入关闭列表，即可在AGV运行过程中，有效地实现路径再规划。

现分别针对无静态物理约束和有静态物理约束这两种情况，进行基于时间因子的A-star算法的算例分析。算例1对应无物理约束的情况，已知初始结点(2,0)，初始方向(1,0)，目标结点(11,9),路径规划结果如图7。这是一个比较理想的情况，在计算过程中，代价估值最小值唯一，所以关闭列表中所有结点构成了最优路径，没有进行多余的运算。

图7 路径规划算例1

算例2和算例3计算的是有静态物理约束的情况。算例2在算例1的基础上引入静态障碍物(11,8)，路径规划结果如图8。算例3在算例2的基础上引入静态障碍物(10,9)，路径规划结果如图9。有静态约束时，关闭列表中搜索过的结点明显增多，计算量增大，特别算例3这一极端情况中，目标结点只有一个远离初始结点的可接近点时，算法搜索了整个地图的大部分区域，不过最后算法仍然得出了最优路径。

图8 路径规划算例2

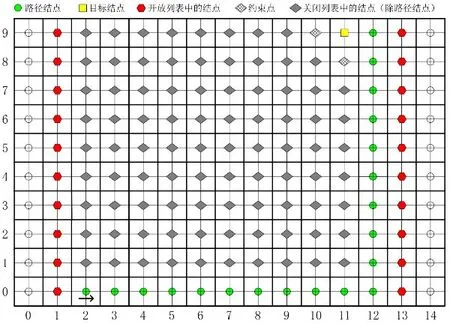
图9 路径规划算例3

算例分析表明此算法针对本文的特定对象，不仅能实现理想状态下的路径规划，在引入静态物理约束时，也可有效解决AGV静态路径全局规划问题，从而可实现AGV的静态路径规划以及动态避障后的路径再规划。

4 AGV群体的动态避障

4.1 障碍检测和碰撞类型

如章节2中的模型假设，AGV在每个栅格间移动时间为1s，在结点上转向时间为1s，抬起和放下货物时间为1s。AGV上传感器检测频率为1次/s，检测半径为6m，即为4个栅格的尺寸大小。为了减少每辆小车的计算量，同时减少传感器数量降低成本，我们在AGV上只放置一个传感器，检测AGV运行方向前方的状态，检测结点如图10所示。

图10 检测区域内结点

在此区域内，检测到障碍物，最快也需2s后才会碰撞。设定小车在每个结点上进行一次检测，检测到障碍物后，小车间进行通信，交互自己当前时刻以及未来2s的坐标及方向，见表1，并在1s内完成计算，决策AGV在下一时间点的动作，完成动态避障。

表1 不同时刻的AGV状态

以A1为例，分别与其他车辆两两比较3个时间点坐标。设两车路径重合点个数为参数c。

若c=0，路径不相交，小车不经过同一结点，不会发生碰撞。

若c=1，有且只有一个重合点，则比较经过此路径结点的时间。两车经过相同点时间集合分别为Ti=(ti1,…,tin)，Tj=(tj1,…,tjn)，设集合P,参数p，ti，tj，p'，ti'，tj'，tk，

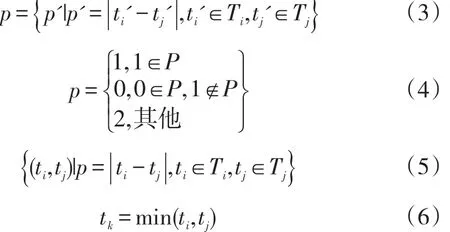
因为AGV本身尺寸问题，两车不仅仅在相同时间点通过同一节点会发生碰撞，在相邻时间点通过也会发生干涉。所以在碰撞判定时会有以下几种情况。

（1）p=2，则两车不碰撞。如图11中a，b两种情况；

（2）p=0，则ti=tj，在此时刻两车发生碰撞，定义此种碰撞类型为定点碰撞，如图11中c，d两种情况；

（3）p=1，tk时刻两车方向不相同，则发生碰撞，定义此种碰撞类型为阻断碰撞，如图11中f情况。

若c=2，有两个重合点，则需判定两车是否是跟随状态，此时有两种情况。

（1）若tk时刻两车的方向相同，则为跟随状态，不发生碰撞，如图11中e情况。

（2）若tk时刻两车方向不同，因有两重合点，则两AGV定相向行驶，轨迹有重叠部分，如图11中g情况，必然发生碰撞。定义此种类型为特殊碰撞（非定点，非阻断）。

图11 碰撞判定

4.2 避障策略与优先级

在本研究对象中，每个AGV都是单独的个体，在同一时刻，分别会对检测范围内的AGV进行碰撞判定。在确定小车间会碰撞之后，每个小车只需判定碰撞类型，选取避障策略，同时根据优先级对AGV在下一结点的动作进行决策，完成整个动态避障过程。

4.2.1 避障策略选取。在AGV动态避障中，有等待策略和路径再规划策略两种方式。

（1）等待策略：优先级低的等待，优先级高按原路径行走；

（2）路径再规划策略：优先级低的重新规划路径，优先级高的等待。

这两种避障策略中，涉及三种动作决策：原路径行驶、等待、路径再规划。AGV在避障决策为路径再规划时，将原路径的下个结点加入关闭列表，再次应用基于时间因子的A-star算法，生成新的路径。

AGV在结点等待只需花费1s，而路径再规划，会至少额外增加1次转向，至少需要1s。所以在避障策略选取时，优先应用等待策略。在避障策略选取时，我们将其分为4种情况。

（1）阻断碰撞时，选取等待策略即可实现避障。

（2）定点碰撞时，如若为图11中c情况，两AGV非相向行驶，选取等待策略即可实现避障。

（3）定点碰撞时，如若为图11中d情况，两AGV相向行驶，则必须进行路径再规划才可实现避障。

（4）特殊碰撞时，两AGV相向行驶，选取路径再规划策略。

碰撞类型和避障策略关系见表2。

表2 碰撞类型与避障策略

4.2.2 优先级比较。在避障策略中，需要基于优先级，进行碰撞AGV的动作决策。所以在系统初始阶段，人为地给系统内所有AGV小车从高到低设定默认优先级就显得尤为必要，其中默认优先级不存在平级。可是在实际运作中，如果仅仅根据默认优先级进行判断，会导致某些AGV小车长期占用，而某些小车却利用率低，同时简单地应用默认优先级，容易出现AGV为了避障而绕路多花时间的情况，效率不高。为了提高资源利用率以及系统整体运行效率，结合路径特点，规定以下优先级规则。

在阻断碰撞的情况下，如图11的f，如果A2优先级低导致等待，则因为A1触发急停设定，导致两AGV的无限等待，所以在阻断碰撞时，比较公式5中ti和tj，先经过相同点的AGV优先级更高。

在非阻断碰撞的情况下，如果从AGV所在结点到目标结点的路径不需要转向，那么在进行路径再规划时，则需要多转向3次，多走2个栅格，即多花5s，如图12中a情况。而原路径需要转向时，只需要多花1s，如图12中b情况。

所以在定点碰撞和特殊碰撞的情况下，考虑到研究对象特点，AGV从当前结点到目标结点的路径不需要转向时，此AGV优先级更高。

设AGV当前结点为(x1,y1)，当前方向为(a1,b1)，目标结点为(x2,y2)，当(x2-x1,y2-y1)的单位向量与(a1,b1)相同时，此AGV至目标结点的路径不需转向，如下式。

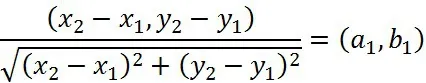
在优先级判断过程中，如若存在相同优先级，则根据默认优先级进行选取。

4.2.3 动态避障决策流程。在避障策略与优先级确认的基础上，AGV可以根据避障策略来决策AGV在下一路径结点的动作：等待、原路径行驶或是路径再规划。在检测区域内有多辆AGV时，则分别与其他AGV进行两两避障决策，最后进行综合避障决策。综合避障决策规则为：路径再规划〉等待〉原路径。即多个避障决策中如果有路径再规划，则总避障决策为路径再规划；如果没有路径再规划，有等待，则总避障决策为等待；否则按照原路径行驶。动态避障决策流程如图13所示。

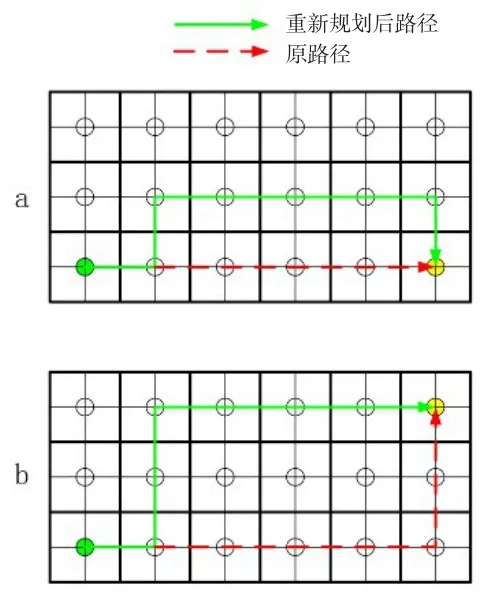
图12 路径再规划

图13 动态避障决策流程图

步骤1：判定AGV碰撞类型；

步骤2：选取AGV避障策略；

步骤3：判定优先级，决策AGV动作，实现两车间的动态避障；

步骤4：分别与检测区域内所有AGV两两进行步骤1至步骤3；

步骤5：进行综合避障决策。

4.3 动态避障算例分析

在AGV群体中，能否避免和解决死锁状态，是整个系统鲁棒性的标志之一。同时在本文中，为了降低成本，减少计算量，只在AGV前方放置感应器，在动态避障中对于后方移动物体并不做考虑。所以本文所提运动规则能否有效避免后车的追击碰撞也是衡量本文运动规则是否有效的指标之一。

为了验证智能AGV群体的运动规则是否有效，现对其进行算例分析。算例中共有5辆AGV，初始路径规划如图14所示。A1、A2、A3、A4的初始路径会在结点(5,4)处产生死锁，同时A2、A5为跟随状态。

图14 初始状态

设图14的当前时刻为0s。AGV群体运行期间，通过避障以及路径再规划，至7s时，完全解开死锁状态，且全程未出现AGV互相干涉的现象。7s时系统状态如图15。

7s内所有AGV的位置方向数据见表3。

算例表明，针对本文的特定对象，结合基于时间因子的AGV路径规划算法以及AGV群体动态避障，可有效实现AGV群体在电子地图内的静态路径规划、动态避障以及避障后的路径再规划。

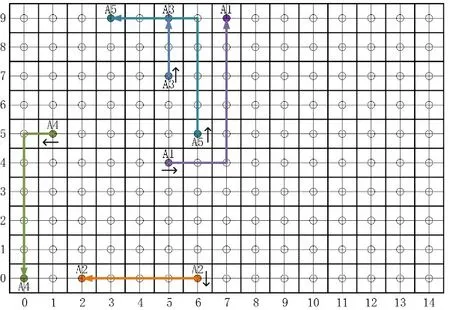
图15 运行7s后状态

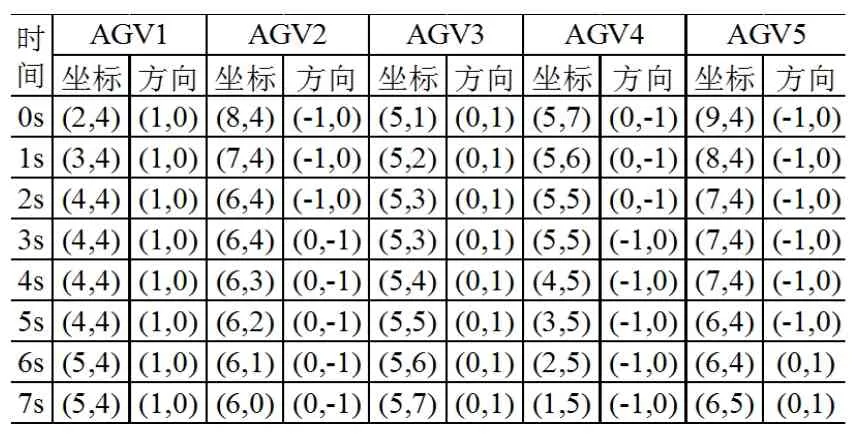
表3 AGV位置方向数据

5 结语

AGV群体的协作并行，是提高搬运效率的重要手段之一。随着物联网和离散控制技术的发展，AGV群体运作模式成为智能物流技术领域的一个重要研究方向，受到众多企业和学者的关注和研究。本文结合静态路径规划与再规划、动态避障两部分研究内容，提出了一种针对自动化立体仓库托盘出入库搬运区域的智能AGV群体的运动机制，并通过算例分析，验证了这种运动机制的有效性。

[1]Christian Prasse,Andreas Nettstraeter,Michael ten Hompel.How IOT will change the design and operation of logistics systems[C].Internet of Things(IOT)IEEE,2014：55-60．

[2]乔岩,钱晓明,楼佩煌.基于改进时间窗的AGVs避障路径规划[J].计算机集成制造系统,2012,18(12)：2 683-2 688．

[3]夏田,王娜.改进蚁群算法在多AGV作业调度中的应用[J].物流技术,2015,(23)：87-89．

[4]冯海双.AGV自动运输系统调度及路径规划的研究[D].哈尔滨：哈尔滨工业大学,2013．

[5]经建峰.基于智能体的多AGV自主控制系统研发[D].南京：南京航空航天大学,2014.

[6]李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京：中国物资出版社,2001．

[7]欧阳圣,胡望宇.几种经典搜索算法研究与应用[J].计算机系统应用,2011,(5)：243-247．

Study on Decision-making in Static Route Planning and Dynamic Barrier Avoidance of Intelligent AGV Group in AS/RS

Fang Dianjun,Zhou Tao
(Chinesisch Deutsches Hochschulkolleg,Tongji University,Shanghai 201804,China)

In this paper,in light of the low automation level of the inbound and outbound handling operations of the AS/RS,and in connection with the development trend of the intelligent logistics industry,we elaborated on the working mode where the forklift truck was replaced by the intelligent AGV group to handle the pallet,and then studied the static route planning and dynamic barrier avoidance decision-making of the AGV group.Next,with the AGV under such working mode as the object,we considered the influence of the time factor on the basis of the A-star algorithm to design the route planning algorithm,next,according to the characteristics of the routing of the AGV on the grid map,presented systematically the collision type and barrier avoidance strategy of the AGV group,and at the end,had a numerical analysis of the route planning,dynamic barrier avoidance and route re-planning of the intelligent AGV group.

intelligent AGV group;route planning;collision type;dynamic barrier avoidance

F253;F253.9

A

1005-152X(2017)06-0170-09

10.3969/j.issn.1005-152X.2017.06.040

2017-04-25

房殿军（1961-），男，山东人，博士，教授，主要研究方向：物流系统规划、供应链管理。