尾缘形状对低压涡轮叶栅气动性能的影响

李 超， 颜培刚， 钱潇如， 韩万金， 王庆超

(哈尔滨工业大学 能源科学与工程学院， 哈尔滨 150001)

尾缘形状对低压涡轮叶栅气动性能的影响

李 超， 颜培刚， 钱潇如， 韩万金， 王庆超

(哈尔滨工业大学 能源科学与工程学院， 哈尔滨 150001)

为减小高负荷低压涡轮叶型损失，提高低压涡轮叶栅气动性能，采用数值模拟方法研究尾缘形状对高负荷前加载低压涡轮叶栅L2F气动性能的影响. 对比尾缘偏斜、增加尾缘厚度和Gurney襟翼对叶栅能量损失和流动的影响. 结果表明：3种尾缘形状都能增加气流折转角, 在低雷诺数时减小能量损失，在高雷诺数时增加损失，但总体上尾缘偏斜提高气动性能的效果更好. 雷诺数为20 000、湍流度为3%时，尾缘偏斜能够减小16.5%叶栅能量损失，增加3.3%气流折转角. 3种尾缘形状都使主流发生偏转，加速了吸力面边界层流动，抑制了流动分离，有利于减小损失；但尾缘改型增强了尾缘后流动掺混，会增加损失.

航空发动机；低压涡轮；尾缘偏斜；气动性能；流动控制

低压涡轮的质量能占到整个发动机质量的30%，包含接近2 000多个叶片[1]. 为了尽可能地减小质量，降低制造成本和运行成本这个目标，设计者强烈倾向于减少叶片数，但这会增加每个叶片的负荷，因此设计者需要设计更高负荷的叶片[2]；无人侦察机(UAVs)在高空巡航时，由于空气密度的降低，低压涡轮运行雷诺数能够降低到25 000以下；在低雷诺数下，吸力面边界层容易分离，甚至不再附，使损失剧烈增加[3]，增加了设计更高负荷的低压涡轮叶型的难度.

设计具有后加载压力分布的叶型能够减小端区损失[4]，但会使吸力面后缘有很大逆压梯度，容易发生严重流分离，需要进行流动控制. 而前加载能够延长吸力侧后部逆压力梯度段长度，在所有位置降低了当地逆压力梯度，提高叶片的抗分离能力，如果发生分离，前加载提供了更长的距离使流动分离再附[5]. Popovic等[6]研究了具有相同负荷系数的前加载叶型PAKD-F和后加载叶型PAKD-A的气动性能，发现前加载PAKD-F的气动性能明显优于后加载PAKD-A，特别是在低雷诺数时，前加载叶型气动性能更加突出. Praisner 等[1]给出了PAK家族系列叶片的气动特性，其中两种新的超高负荷叶型PAKE(负荷系数为1.6和1.8)都是采用的前加载设计. Mcquilling[7]指出，在所有飞行状态下，最强健的低压涡轮叶型设计都应该是前加载的. 虽然前加载叶型具有良好的气动特性，但前加载也有一些缺点，比如前加载叶片发生转捩靠前，在叶片吸力面有较长的湍流区域，这会导致损失增加[8]. Roberts[9]发现可以通过尾缘改型减小损失. Zhou等[10]和李超等[11]研究发现，改变尾缘厚度影响低压涡轮能量损失，增加尾缘厚度能减小高负荷低压涡轮叶栅的能量损失. Byerley等[12]及乔渭阳等[13-14]通过Gurney襟翼来控制流动分离，襟翼能够减小流动分离，推迟转捩，减小损失.

尾缘偏斜最初用于调整飞机机翼形状,以适应飞机不同气动条件[15]. 后来科研工作者将尾缘偏斜用于风力机上，用来控制风力机叶片负荷和气动性能. Daynes 等[16]研究通过尾缘偏斜控制风机涡轮负荷. Wolff等[17]研究了尾缘偏斜对风机叶片气动性能的影响. 尾缘偏斜也可以用于控制低压涡轮叶栅流动分离，提高叶栅气动性能[18].

本文首先将低压涡轮静压和损失的计算结果和实验结果进行对比，验证数值计算方法准确性，然后在此基础上研究比较了尾缘偏斜(DT)、尾缘厚度(IT)和Gurney襟翼(GT)3种不同尾缘形状对高负荷叶栅气动性能的影响，分析了尾缘形状对低压涡轮流动控制的机理.

1 研究对象及数值计算方法

本文研究对象是由Mcquilling[7]设计的高负荷前加载叶型L2F. L2F速度峰值在26%轴向弦长处；和典型的低压涡轮叶栅Pak-B相比，L2F负荷提高了38%；叶栅参数见表1.

表1 低压涡轮叶栅基本参数

负荷系数Zw(Zweifel lift coefficient)的定义为

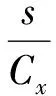
(1)

式中:s为栅距，Cx为轴向弦长，C为弦长,uin和uout分别是叶栅进出口轴向速度,βin和βout分别是进出口气流角.

图1给出了叶片尾缘形状示意图.

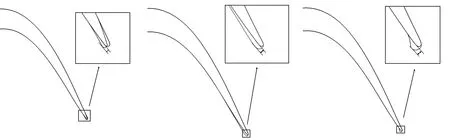
图1 尾缘形状示意

在约距离前缘95%轴向弦长处，尾缘是从吸力侧向压力侧偏斜，尾缘偏斜高度为h，如图1(a)所示. 为了减小对吸力侧边界层的影响，增加尾缘厚度时吸力侧曲线保持不变[10]，只改变了压力侧曲线，吸力侧曲线和压力侧曲线相对中弧线对称，增加的尾缘厚度为t，如图1(b). 图1(c)给出了Gurney襟翼示意图，襟翼高度为g. L2F原型叶片h=0，t=0，g=0.

图2是计算网格，叶片周围采用O型网格，叶片近壁面加密，第一层网格y+<1，伸缩比是1.1；为了减少计算量，沿着径向方向布置了2个网格节点，在展向和弦向设置周期边界，并进行了网格独立性验证，选定网格总数为230 k进行计算.

湍流模型采用SST湍流模型，转捩模型采用Langtry-Menter转捩模型[19-20]. 进口边界给定总压、总温、气流角度、来流湍流度和涡黏比. 出口边界给定平均静压；叶片壁面是无滑移边界条件，进口边界条件如表2所示. 为了比较尾缘改型对叶栅气动性能的影响，3种尾缘形状叶栅的进口边界条件是相同的.

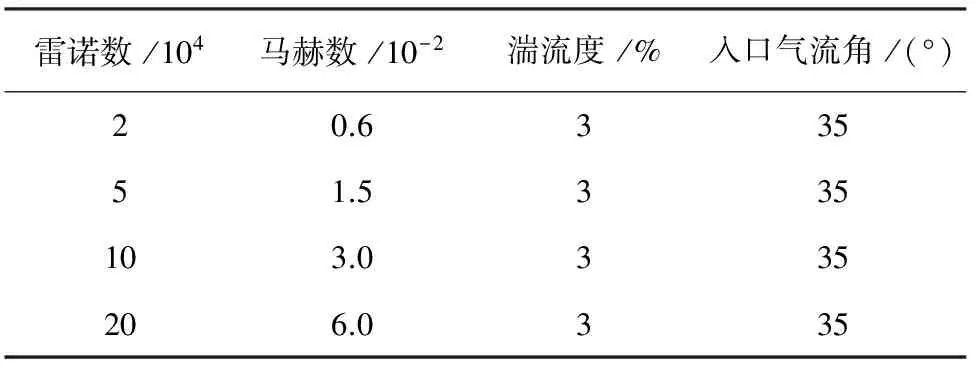
表2 计算边界条件

图2 尾缘处计算网格

2 计算方法验证

本文参考的实验数据来自Lyall等[21]、Benton等[22]对L2F叶栅做的系列实验. 本文的雷诺数Re是基于入口速度和轴向弦长Cx，来流湍流度均为3%. 静压系数Cp的定义：

Cp=(pTinlet-p)/(pTinlet-pinlet)，

式中:p是静压，pTinlet进口总压，ρ为密度，u为速度. 基于进口速度的能量损失系数γ为

γ=(pTinlet-pToutlet)(pTinlet-pinlet)，

其中pToutlet为出口总压.

图3是叶片表面静压系数Cp分布. 量纲一高度H=h/C，T=t/C，G=g/C. 从图3可以看出,计算结果和实验结果吻合得很好，在Re=20 000时，L2F没有发生完全分离； 随着雷诺数增大，分离泡减小. 图4是雷诺数对能量损失系数的影响. 从图4可以看出，L2F能量损失系数计算值和实验结果吻合得很好,和Pak-B相比，L2F展现出很好的低雷诺数特性；在Re=20 000时，L2F能量损失系数比Pak-B降低了约60%. 从图3和图4可以看出，采用的数值计算方法能够准确地捕捉叶栅内流动分离和转捩过程，预测叶栅的能量损失.

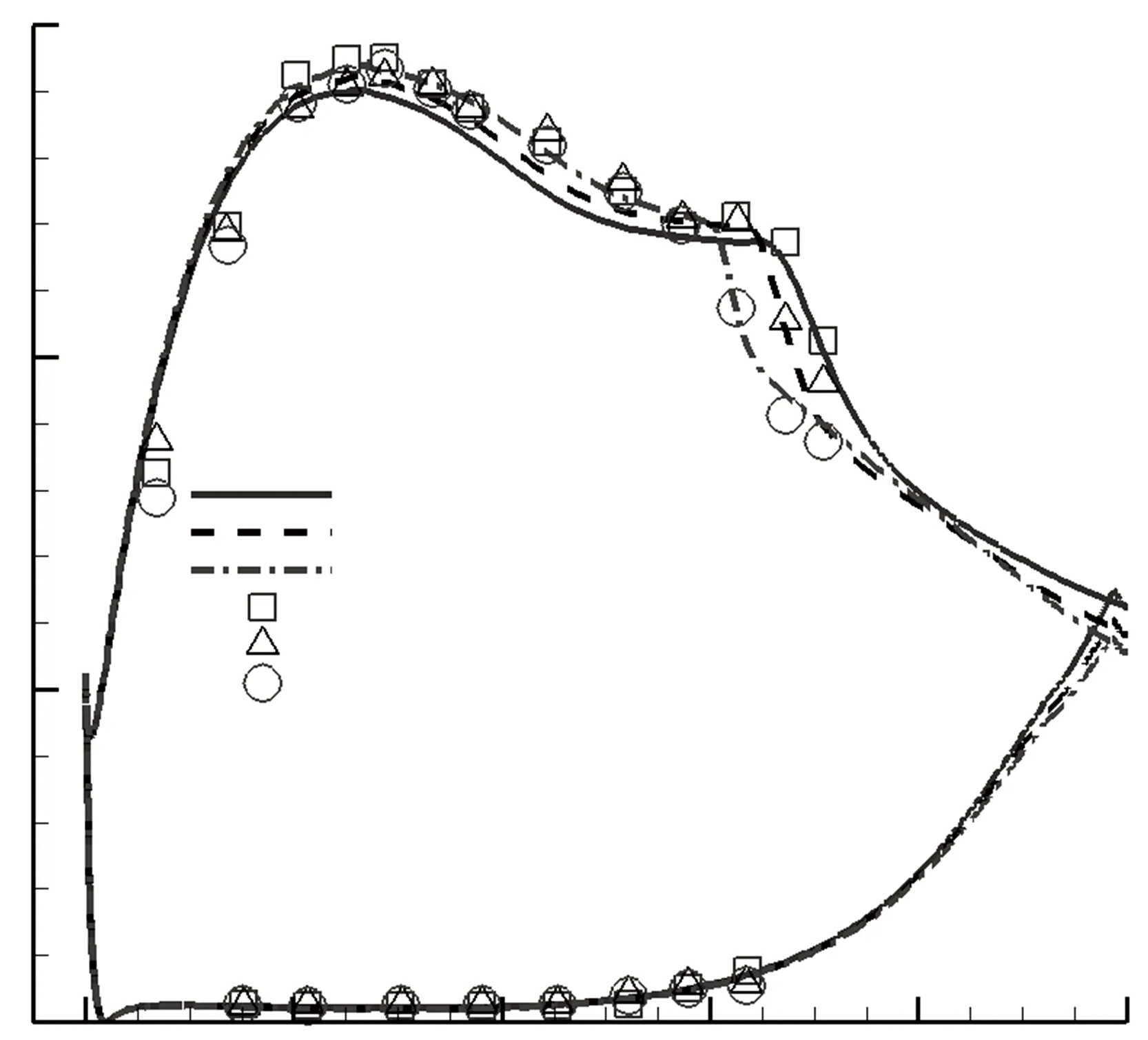
图3 静压系数分布

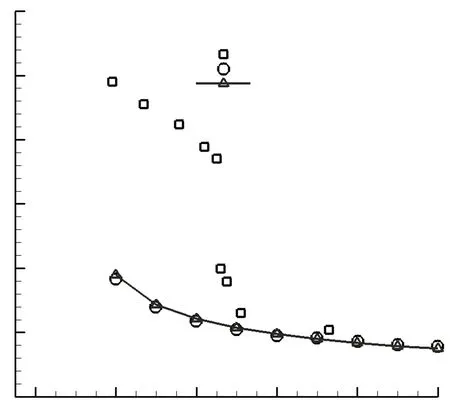
图4 雷诺数对能量损失系数的影响

3 计算结果分析

3.1 不同尾缘形状对低压涡轮叶栅影响的对比

图5给出了量纲一高度对能量损失系数的影响，可以看出，和原型叶栅相比，尾缘偏斜(DT)、增加尾缘厚度(IT)和Gurney襟翼(GT)都能够在低雷诺数时(Re=20 000，Re=50 000)减小叶栅能量损失. 但在高雷诺数时(Re=100 000，Re=200 000)，3种尾缘形状会增加损失. 尾缘偏斜和襟翼在Re=20 000时能量损失相当，并且都小于增加尾缘厚度的，其中尾缘偏斜H=0.015时，能量损失最小. 雷诺数为20 000、湍流度为3%时，尾缘偏斜能够减小叶栅能量损失16.5%，增加气流折转角3.3%. 而在更高雷诺数时，总体上叶片尾缘偏斜的叶栅能量损失比叶片增加襟翼和尾缘厚度的能量损失小. 图6给出了量纲一高度对叶栅气流折转角的影响，可以看出，随着量纲一高度的增加，叶栅的气流折转角增加. 但尾缘偏斜和襟翼的气流折转角都大于增加尾缘厚度的. 结合图5和图6可以看出，从整体上，叶片尾缘偏斜提高低压涡轮叶栅气动性能的效果最好.

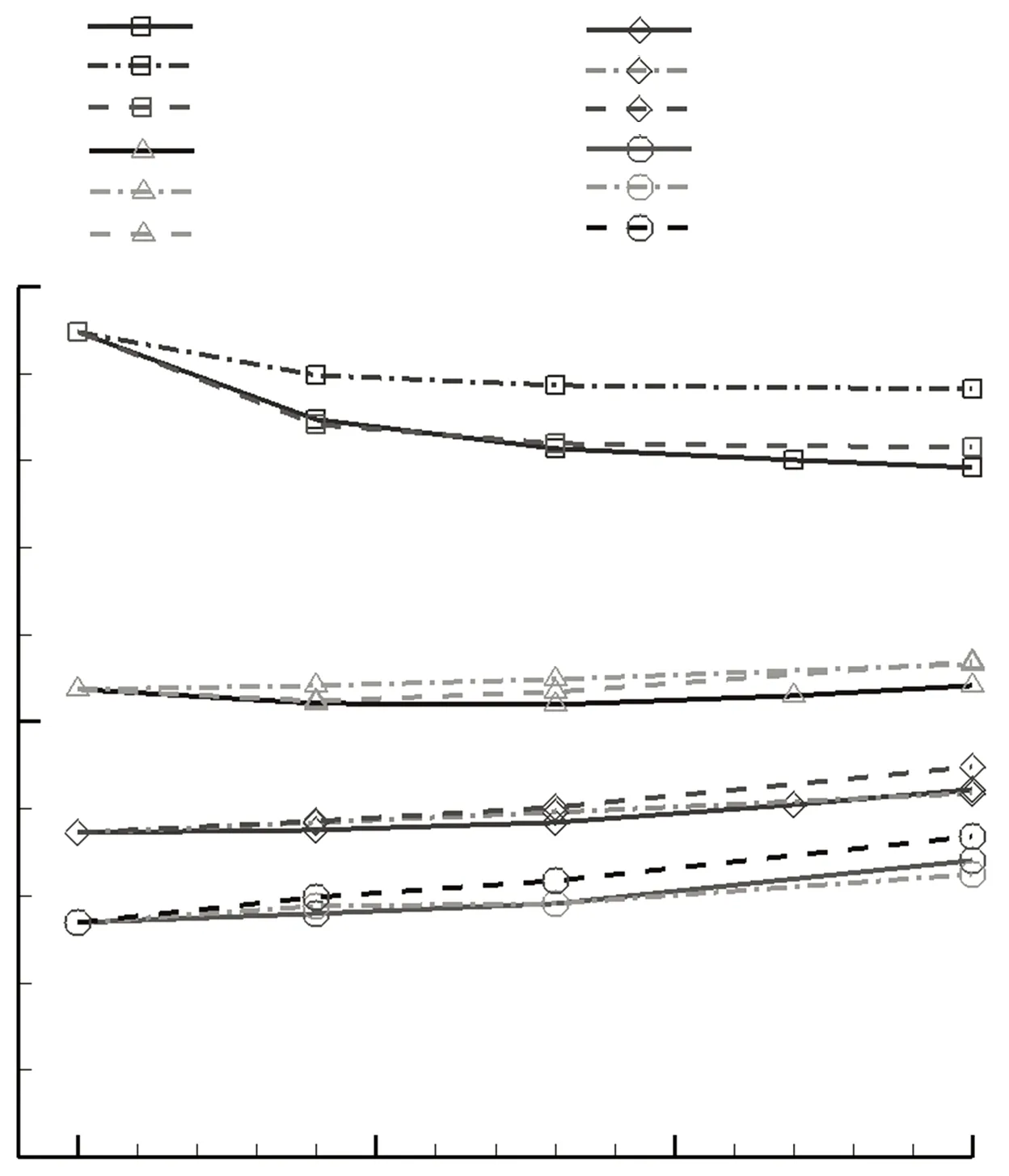
图5 量纲一高度对叶栅能量损失系数的影响

Fig.5 Effects of dimensionless height on the energy loss coefficient

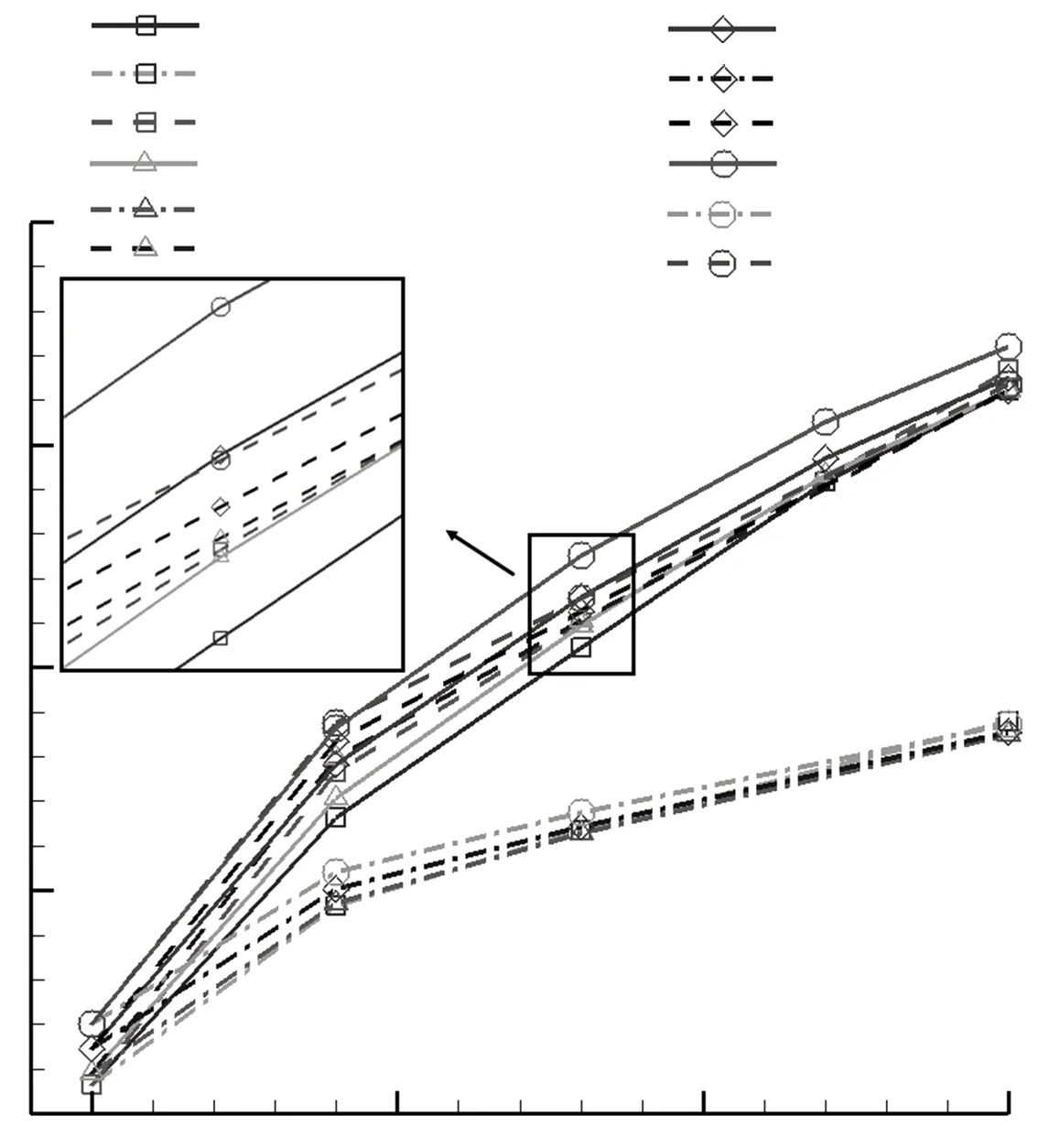
图6 量纲-高度对叶栅气流折转角的影响

Fig.6 Effects of dimensionless height on the flow turning angle

3.2 尾缘形状对叶栅流动的影响

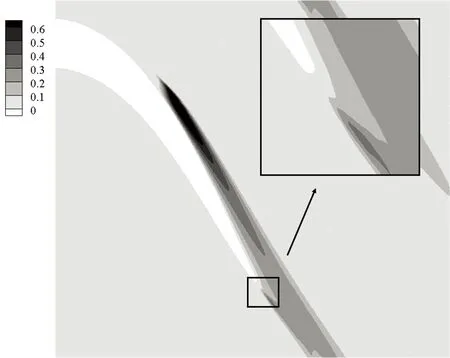
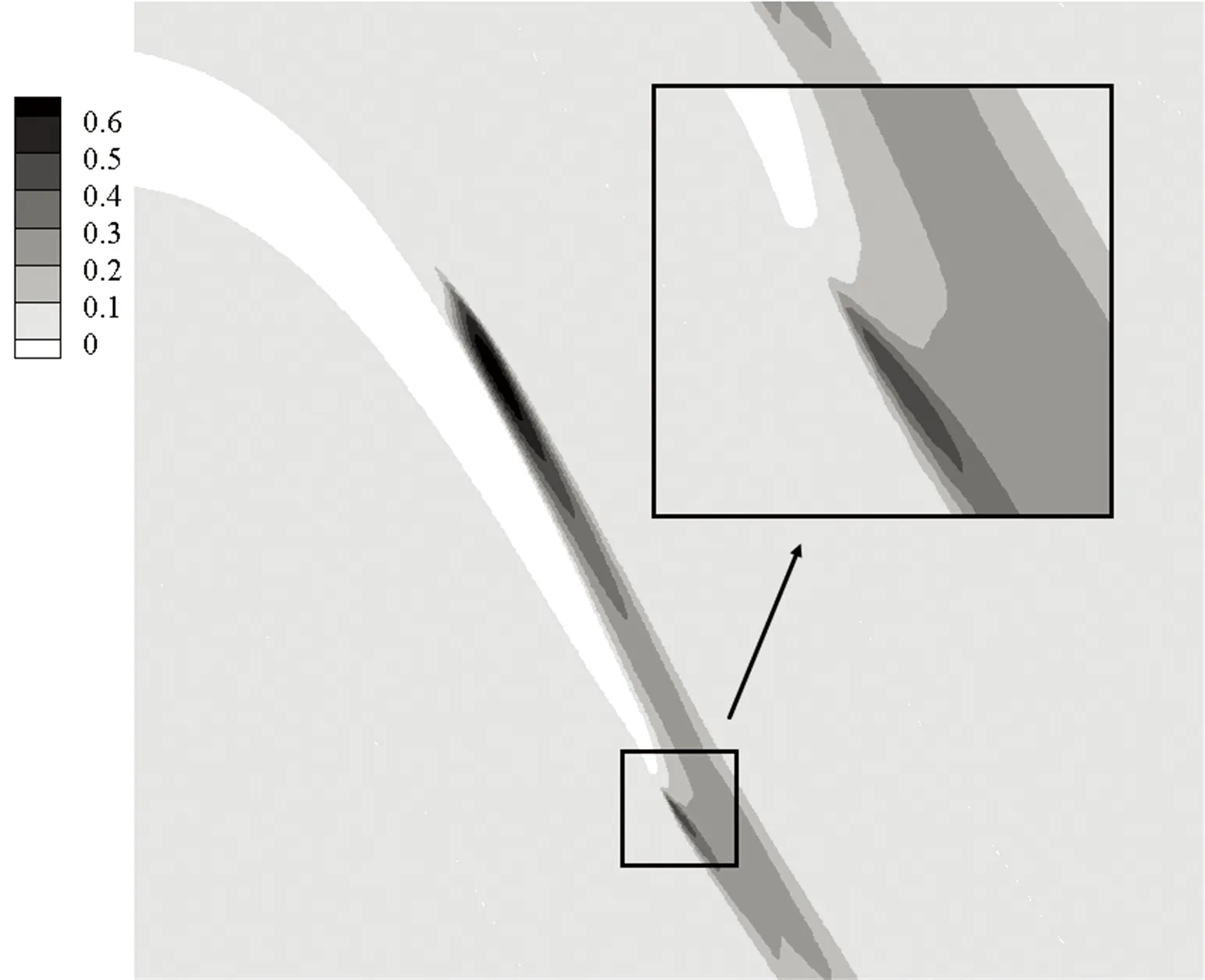
以量纲一高度(G、T、H)等于0.008为例分析尾缘形状对叶栅流动的影响. 图7给出了静压系数分布. 可以看出,3种尾缘形状都推迟了流动分离，分离点和再附点的位置基本相同. 图8为流线和速度云图，可以看出，和原型叶栅相比，3种尾缘形状都使主流发生偏转，加速了吸力面边界层流动，抑制了流动分离，减小了分离泡. 在相同量纲一高度时，3种尾缘形状减小分离泡程度基本相同. 从图8还可以看出，尾缘改型在减小吸力面分离泡的同时，也增强了尾缘处流动掺混，尾缘后都形成了不同尺度的漩涡，其中尾缘偏斜形成的漩涡最小，襟翼形成的漩涡最大.

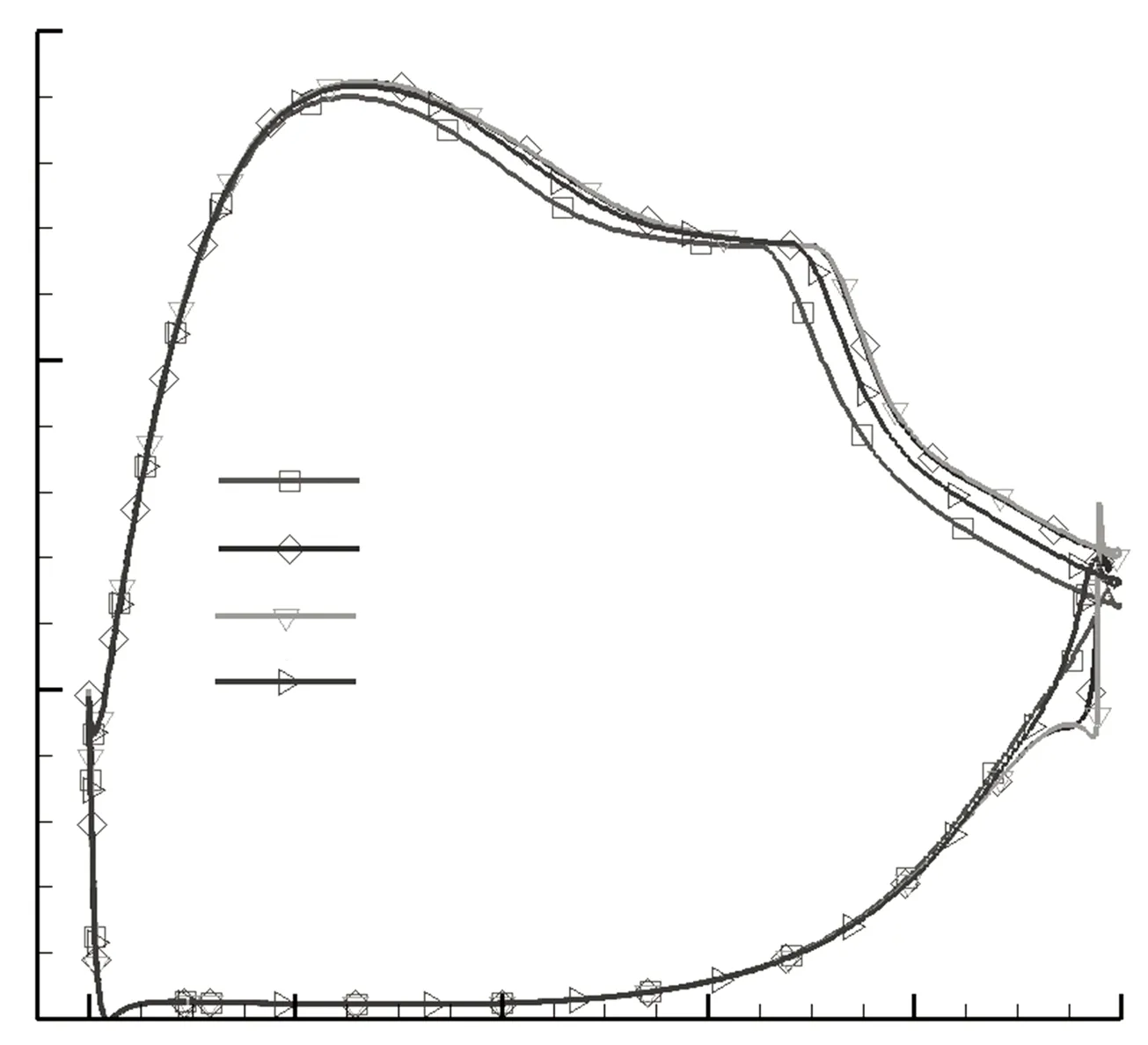
图7 Re=20 000时静压系数分布

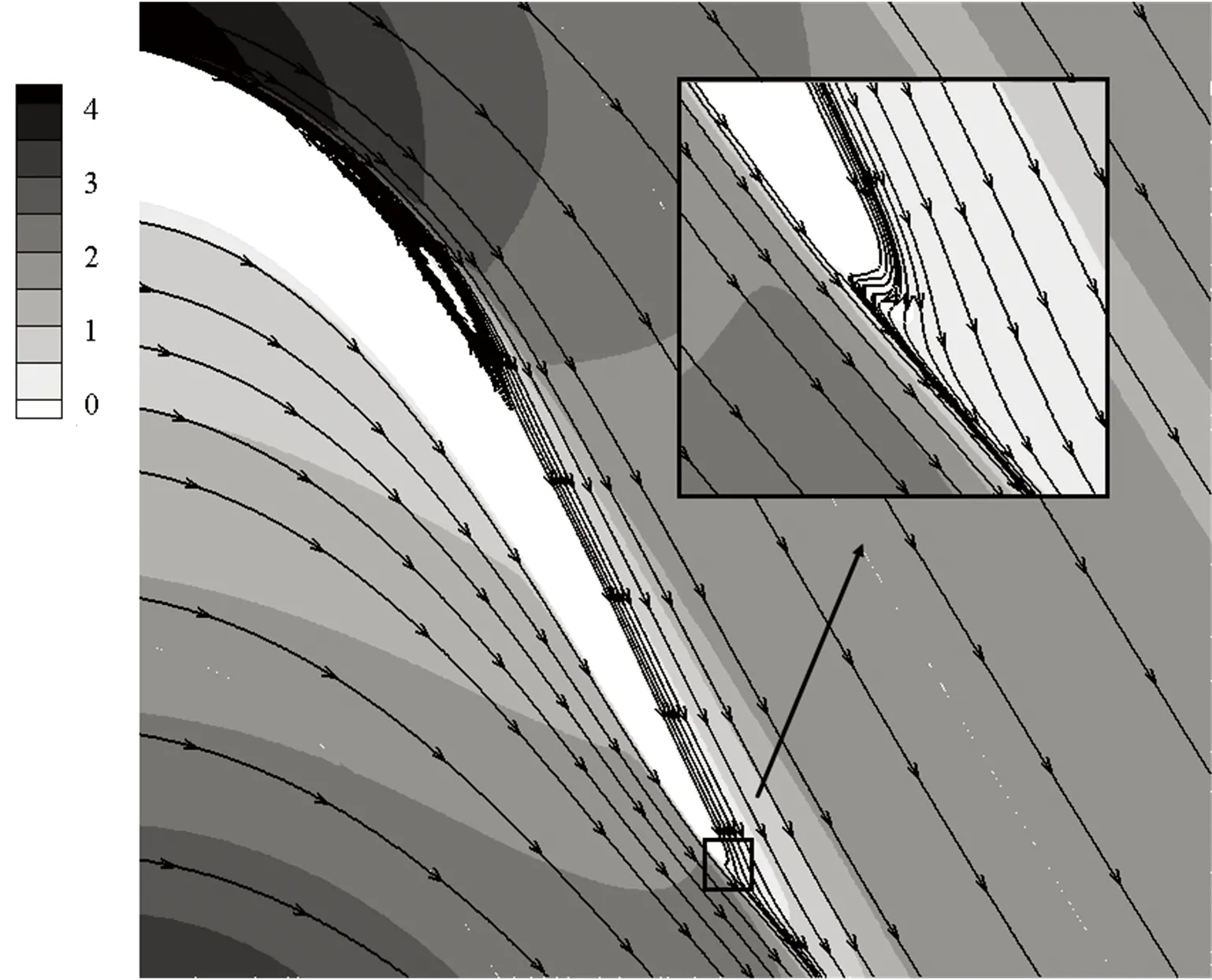
(a)原型叶栅

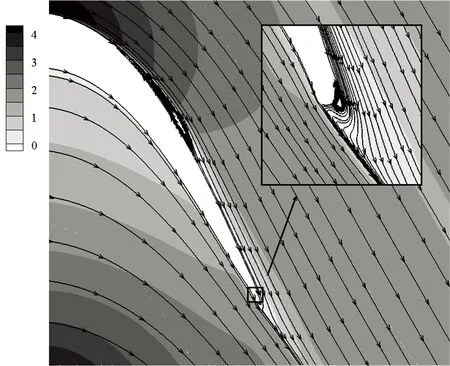
(b)H=0.008

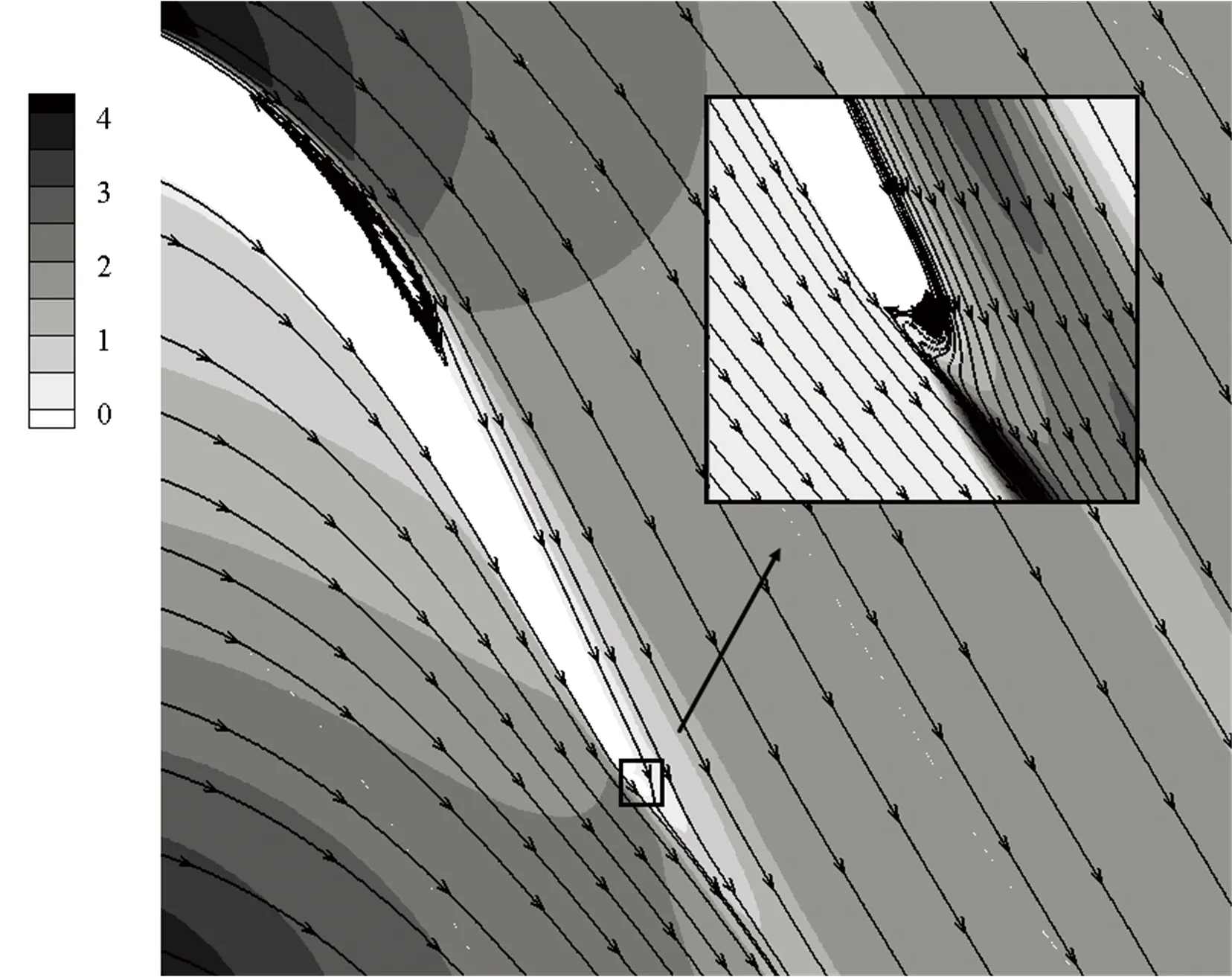
(c)T=0.008

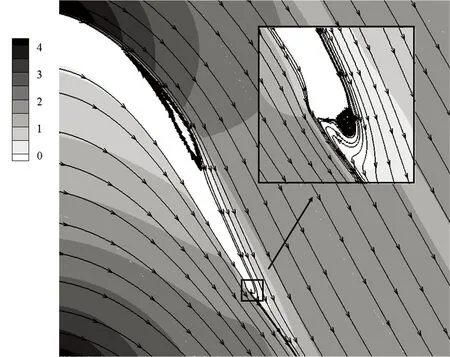
(d)G=0.008

图9是3种尾缘形状的叶栅内湍动能云图，由于尾缘改型加速了边界层流动，转捩点向下游移动，高湍流度区域面积和强度减小，但尾缘改型增强了尾缘后湍动能强度，尾缘偏斜没有明显增强尾缘后湍动能，而襟翼后湍动能强度和吸力面上湍动能强度相当. 增加尾缘厚度和Gurney襟翼的流动控制机理和尾缘偏斜的相同，一方面抑制流动分离，减小能量损失，另一方面，增强了流动掺混，增加了损失.

(a) 原型

(b)H=0.008

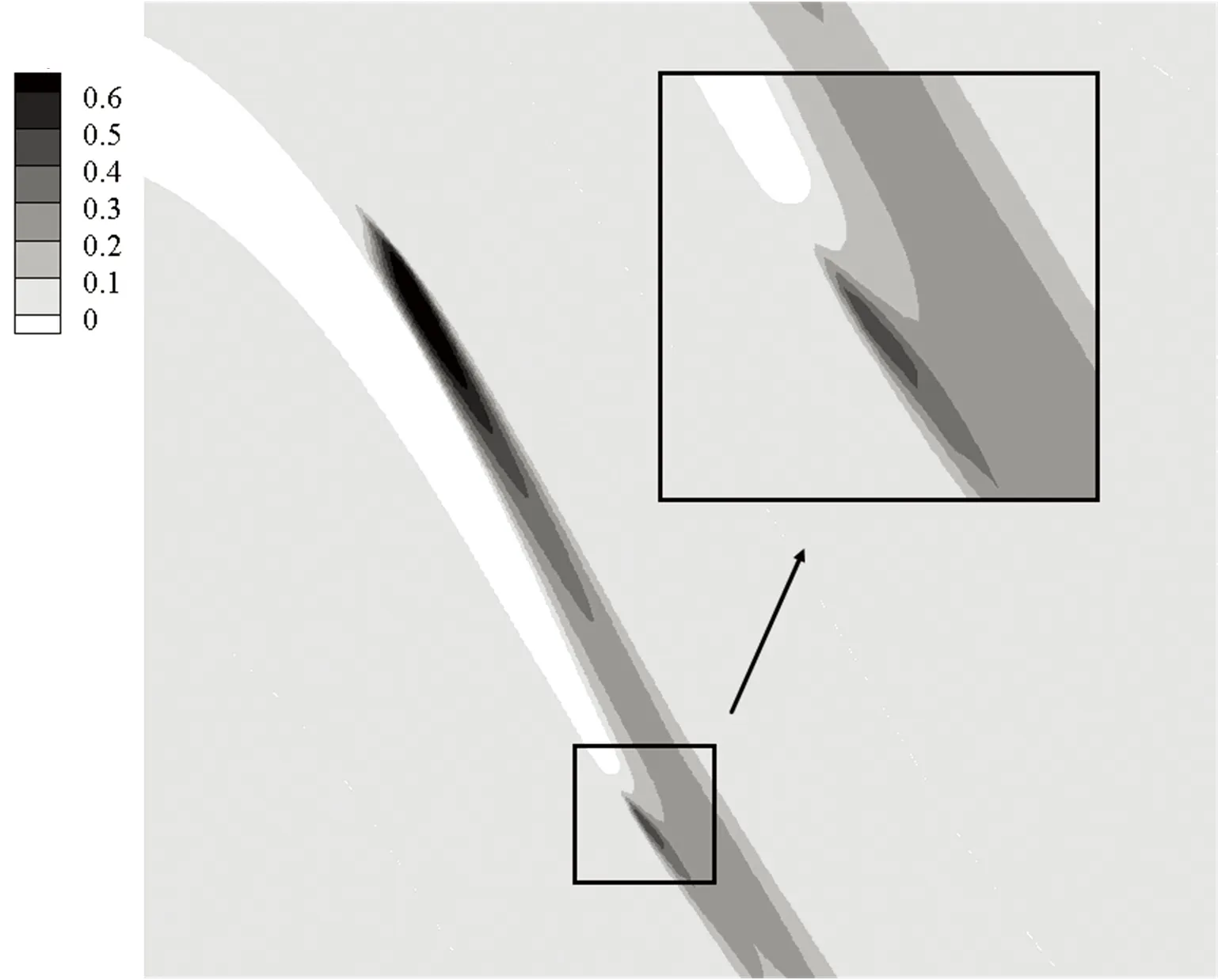
(c)T=0.008

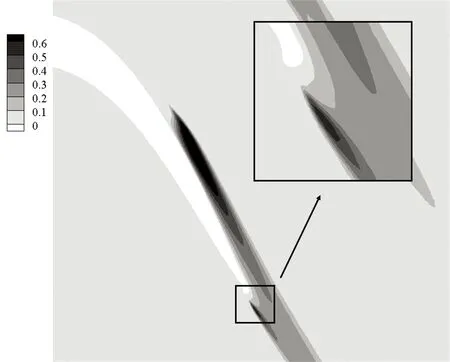
(d)G=0.008

尾缘偏斜(DT)、增加尾缘厚度(IT)和Gurney襟翼(GT)在提高低压涡轮叶栅气动性能的同时，减小喉部和栅距的比值，从而减小了每一级的质量流量. 为了保持每一级的质量流量不变，对量纲一高度(H、T、G)为0.04、0.08、0.15的叶栅，栅距分别增加约0.60%, 1.20%, 2.25%. 图10给出了量纲一高度对栅距增加后能量损失系数和气流折转角的影响. 可以看出，增加栅距后，3种尾缘形状同样能在低雷诺数时减小叶栅能量损失，增加气流折转角. 在低雷诺数条件时(Re=20 000)，增加栅距会使3种尾缘改型叶栅能量损失增加，但尾缘偏斜叶栅能量损失最小，而增加尾缘厚度叶栅的能量损失最大；增加栅距还减小了叶栅的气流折转角，但尾缘偏斜和襟翼叶栅的气流折转角相当，增加尾缘厚度叶栅的最小. 所以增加栅距后，低雷诺数条件下尾缘改型都能提高低压涡轮叶栅的气动性能，但尾缘偏斜的气动性能最好.

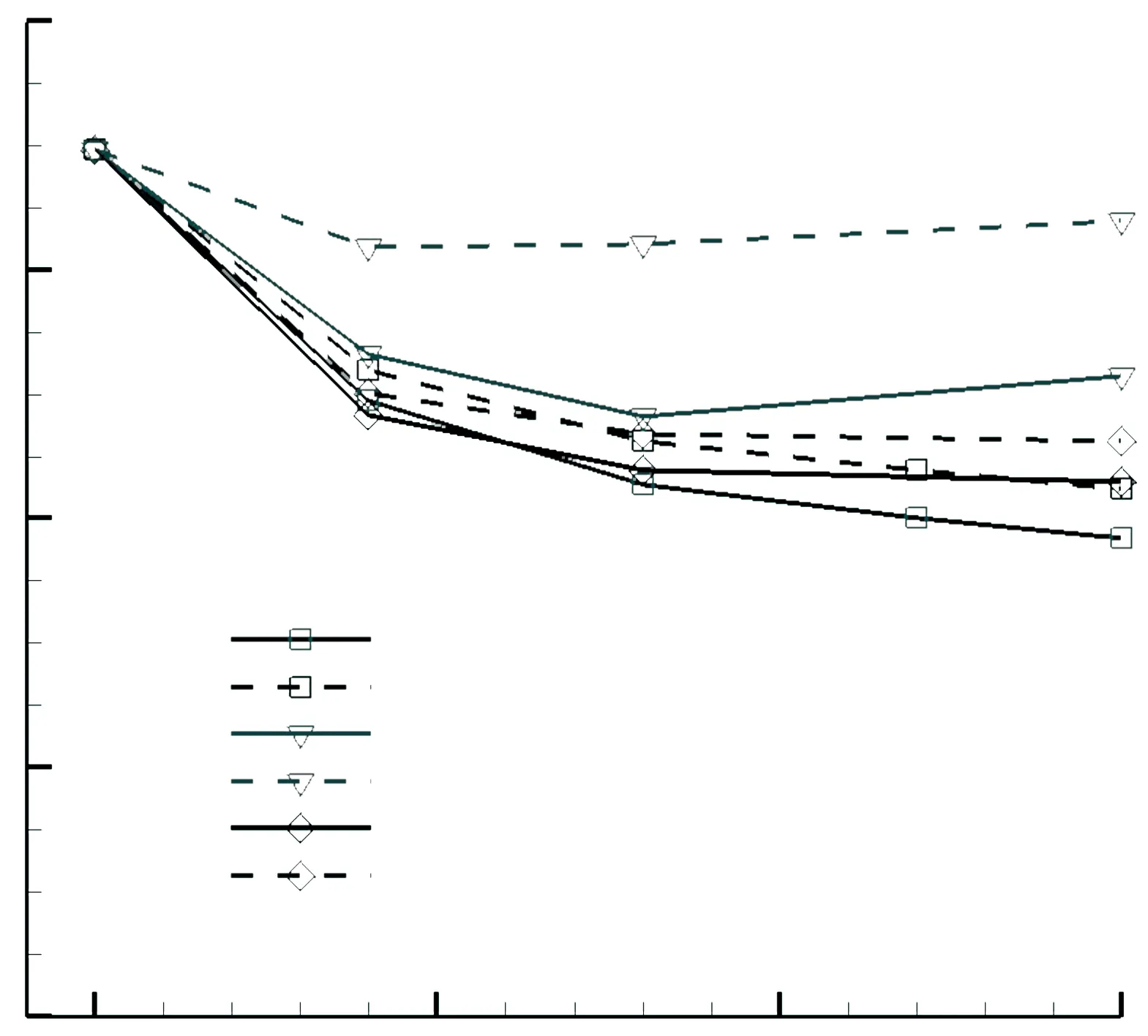
(a)能量损失系数

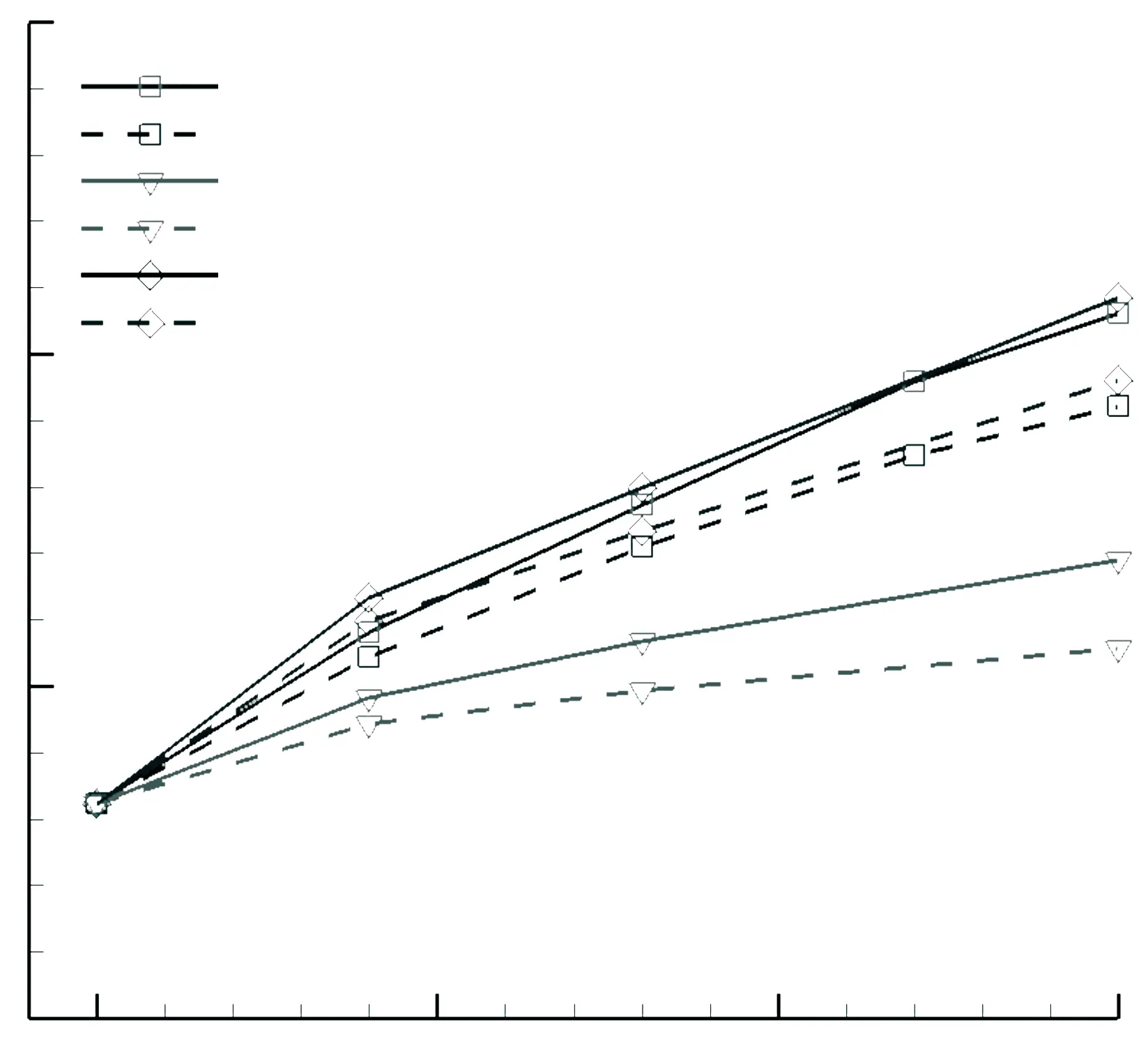
(b)气流折转角

图10Re=20 000时量纲一高度对能量损失系数和气流折转角的影响
Fig.10 Effects of dimensionless height on the energy loss coefficient and the influence of air flow turning angle,Re=20 000

4 结 论

1)尾缘偏斜，增加尾缘厚度和Gurney襟翼都能减小低压涡轮叶栅能量损失，增加气流折转角；但从整体上，尾缘偏斜比其他两种尾缘形状效果好.

2)3种尾缘形状的流动控制机理相同，都加速了吸力面边界层流动，抑制了流动分离，可以减小能量损失；但都增强了尾缘后流动掺混，这会增加损失.

3)增加栅距，保持主流流量不变，3种尾缘形状同样能够减小叶栅能量损失，增加气流折转角，但尾缘偏斜叶栅的气动性能最好. 尾缘形状设计对高负荷低压涡轮叶栅气动性能有重要影响. 尾缘偏斜可以应用到更高负荷低压涡轮叶型尾缘设计中.

[1] PRAISNER T J, GROVER E A, CLARK J P, et al. Toward the expansion of low-pressure-turbine airfoil design space[C]// ASME Turbo Expo 2008: Power for Land, Sea, and Air. Berlin: American Society of Mechanical Engineers, 2013:1323-1331.

[2] Van TREUREN K W, SIMON T, von KOLLER M, et al. Measurements in a turbine cascade flow under ultra low Reynolds number conditions[J]. Journal of Turbomachinery, 2002, 124(1): 100-106. DOI:10.1115/GT2008-50898.

[3] VOLINO R J. Separated flow transition under simulated low-pressure turbine airfoil conditions-part 1: mean flow and turbulence statistics[J]. Journal of Turbomachinery, 2002, 124(4):691-702. DOI:10.1115/GT2002-30236.

[4] WEI A P, FOTTNER L. The influence of load distribution on se-condary flow in straight turbine cascades[J]. Journal of turbomachinery, 1995, 117(1): 133-141.DOI:10.1115/1.2835631.

[5] VOLINO R J, KARTUZOVA O, IBRAHIM M B. Experimental and computational investigations of low-pressure turbine separation control using vortex generator jets[C]// Proceedings of ASME Turbo Expo 2009: Power for Land, Sea, and Air. [s.l.]: American Society of Mechanical Engineers, 2009: 1105-1117.DOI: 10.1115/GT2009-59983.

[6] POPOVIC I, ZHU J, DAI W, et al. Aerodynamics of a family of three highly loaded low-pressure turbine airfoils: measured effects of reynolds number and turbulence intensity in steady flow[C]//ASME Turbo Expo 2006: Power for Land, Sea, and Air. Barcelona: American Society of Mechanical Engineers, 2006: 961-969.

[7] MCQUILLING M W. Design and validation of a high-lift low-pre-ssure turbine blade[D]. Ohio state: Wright State University, 2007.

[8] ZHANG X F, VERA M,HODSON H, et al. Separation and transition control on an aft-loaded ultra-high-lift LP turbine blade at low Reynolds numbers: low-speed investigation[J]. Journal of Turbomachinery, 2006, 128(3): 517-527.DOI:10.1115/1.2187524.

[9] ROBERTS Q D H. The trailing edge loss of subsonic turbine blades [D]. Cambridge: University of Cam-bridge, 1998.

[10]ZHOU C, HODSON H, HIMMEL C. The effects of trailing edge thickness on the losses of ultra-high lift LP turbine blades[C]//ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. Texas: American Society of Mechanical Engineers, 2013: V06AT36A001-V06AT36A001.

[11] 李超, 颜培刚, 韩万金, 等. 尾缘厚度对低压涡轮气动性能影响的数值模拟[J]. 航空动力学报, 2016 (1): 106-114.

LI Chao, YAN Peigang, HAN Wanjin, et al. Numerical simulation of the effects of trailing edge thickness on aerodynamic performance of low pressure turbine[J]. Journal of Aerospace Power, 2016 (1):106-114.

[12]BYERLEY A R, STOMER O, BAUGHN J W, et al. Using gurney flaps to control laminar separation on linear cascade blades[C]//ASME Turbo Expo 2002: Power for Land, Sea, and Air. Amsterdam: American Society of Mechanical Engineers, 2002: 1191-1199.

[13]张军胜, 乔渭阳, 孙大伟. 基于Gurney襟翼的低压涡轮叶栅流动控制实验[J]. 航空动力学报, 2009, 24(5):1129-1135.

ZHANG Junsheng, QIAO Weiyang, SUN Dawei. Experiment on flow control using Gurney-flaps for a low-pressure turbine cascade[J]. Journal of Aerospace Power, 2009, 24(5):1129-1135.

[14]CHEN P P, QIAO W Y, LUO H L. Investigation of low solidity LP turbine cascade with flow control: part 2—passive flow control using gurney-flap[C]//ASME Turbo Expo 2010: Power for Land, Sea, and Air. Glasgow: American Society of Mechanical Engineers, 2010: 1155-1162.

[15]SOFLA A Y N, MEGUID S A, TAN K T, et al. Shape morphing of aircraft wing: Status and challenges[J]. Materials & Design, 2010, 31(3):1284-1292. DOI: 10.1016/j.matdes.2009.09.011.

[16]DAYNES S, WEAVER P M. Design and testing of a deformable wind turbine blade control surface[J]. Smart Materials and Structures, 2012, 21(10): 105019. DOI: 10.1088/0964-1726/21/10/105019.

[17]WOLFF T, ERNST B,SEURME J R. Aerodynamic behavior of an airfoil with morphing trailing edge for wind turbine applications[J]. Journal of Physics, 2014, 524(1): 012018.

[18]LI Chao,YAN Peigang,WANG Xiangfeng, et al. Use deflected trailing edge to improve the aerodynamic performance and develop low solidity LPT cascade [J/OL]. [2016-03-03]. http://www.degruyter.com/view/j/tjj.ahead-of-print/tjj-2016-0005/ tjj-2016-0005.xml

[19]MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables-Part I: model formulation [J]. Journal of turbomachinery, 2006, 128(3): 413-422.DOI:10.1115/1.2184352.

[20]LANGTRY R B,MENTER F R, LIKKI S R, et al. A correlation-based transition model using local variables-part II: test cases and industrial applications [J]. Journal of Turbomachinery, 2006, 128(3): 423-434.DOI:10.1115/1.2184353.

[21]LYALL M E, KING P I, SONDERGAARD R, et al. An investigation of reynolds lapse rate for highly loaded low pressure turbine airfoils with forward and aft loading[J]. Journal of Turbomachinery, 2012, 134(5): 051035.DOI: 10.1115/1.4004826.

[22]BENTON S I, BONS J P, SONDERGAARD R. Secondary flow loss reduction through blowing for a high-lift front-loaded low pressure turbine cascade[J]. Journal of Turbomachinery, 2013, 135(2): 021020. DOI: 10.1115/1.4007531.

(编辑 杨 波)

DOI：10.11918/j.issn.0367-6234.201603132

Effects of deflected trailing edge on the aerodynamic performance of high-lift low pressure turbine cascades

LI Chao, YAN Peigang, QIAN Xiaoru, HAN Wanjin, WANG Qingchao

(School of Energy Science and Power Engineering, Harbin Institute of Technology, Harbin 150001, China)

To reduce the energy loss of high-lift low pressure turbine (LPT) and improve the aerodynamic performance, numerical simulation method was used to study the effects of trailing edge shapes on the aerodynamic performance of high-lift LPT L2F cascades. The effects of three trailing edge shapes, deflected trailing edge, increasing trailing edge thickness and the Gurney flap on the energy loss and flow were studied. It is shown that the three trailing edge shapes all can increase flow turning angle, decrease energy loss coefficient at low Reynolds number (Re) and increase the energy loss at highRe, however the deflected trailing edge is more effective than the others to improve the aerodynamic performance of the LPT cascades. Deflected trailing edge decrease energy loss by 16.5% atReof 20 000 and free-stream turbulence intensities (FSTI) of 3.3%. The three trailing edge shapes deflected the main flow, accelerate boundary layer flow on the suction side, and suppress the flow separation, which tend to decrease the energy loss. However the three trailing edge shapes enhance the mixing flow behind the trailing edge, which tend to increase the energy loss.

aircraft engine; low pressure turbine; deflected trailing edge; aerodynamic performance; flow control

10.11918/j.issn.0367-6234.201607026

2016-07-08

国家自然科学基金委创新研究群体(51421063)

李 超(1986—)，男，博士研究生； 颜培刚(1975—)，男，教授，博士生导师； 王庆超(1950—)，男，教授，博士生导师； 韩万金(1942—)，男，教授，博士生导师

韩万金，hanwanjin@hit.edu.cn

V231.3

A

0367-6234(2017)07-0057-06