西鞍山矿区地下水水质评价

张路

摘要：地下水水质评价具有随机性及模糊性等不确定性特点，本文以西鞍山矿区为例，采用基于云模型的综合评价方法对取样点地下水水质进行了评价，并将结果与BP人工神经网络、模糊综合评价结果对比，对比结果证实云模型在地下水水质评价中具有较好的适用性。评价过程充分考虑了地下水水质的随机性及模糊性，过程简便、结果合理，可为相似水质评价提供技术参考。

Abstract： The evaluation of groundwater quality is characterized by randomness and ambiguity. In this paper， taking Xi'anshan mining area as an example， the groundwater quality of sampling points is evaluated by using the comprehensive evaluation method based on cloud model， and the results are compared with BP artificial neural network and fuzzy comparison results. The result shows that the cloud model has a good applicability in the evaluation of groundwater quality. The evaluation process takes into account the randomness and ambiguity of groundwater quality， and the process is simple and the results are reasonable， which can provide technical reference for similar water quality evaluation.

关键词：地下水水质；云模型；不确定性；综合评价

Key words： groundwater quality；cloud model；uncertainty；comprehensive evaluation

中图分类号：X824 文献标识码：A 文章编号：1006-4311（2017）21-0223-03

0 引言

水质的优劣是确定水源优良程度的重要标准。目前水质评价的方法众多，传统评价主要为指数评价法，包括单因子评价法[1]及综合污染指数法[2]，指数评价法运用简便，可对水体水质是否达标进行判别，但不能对综合水质类别进行评价。近年来，随着计算机及模糊数学等的发展，国内外学者研究出了一系列水质评价的新方法，如物元分析法[3]、灰色系统评价法[4]、人工神经网络模型[9]、模糊综合评价法[5]等，各类方法特点不同、各有优劣，但都未充分考虑到评价过程的不确定性。本文以李德毅院士[6]提出的云模型理论为基础，建立地下水水质评价模型，综合考虑评价过程中的不确定性，并结合实例验证模型的有效性。

1 云模型原理

云模型由李德毅等于1995年提出，可实现定性概念向定量数值的转换，現已在数据挖掘、信任管理和综合评价等多个领域得到应用[7]。

1.1 云的定义

设U是一个定量论域，用精确数值表示，而C是U上的定性概念，若存在定量值x∈U，且x是定性概念C的一次随机实现，x对C的确定度μ（x）∈[0，1]是具有稳定倾向的随机数，即：

u：U→[0，1] ？坌x∈U x∈u（x）

则x在论域U上的分布称为云，每一个x称为一个云滴。

1.2 云的数字特征

云理论是一种定性概念定量化的研究方法。定性概念转换成定量值，是一个具有偶然性的、离散的转换过程。云滴的确定度反映了不确定性，该值本身也是一个随机值，可用其概率分布函数具体描述。云模型可用3个数字特征，即期望Ex、熵En和超熵He来整体表征一个概念[6]。

1.3 云算法

云算法包括正向、逆向两类。本文模型采用了正向正态云算法，正向云算法能够实现从数字特征表示的定性概念向定量数据的转化，即基于云模型的3个数字特征，计算输出N个云滴的定量值及由这些云滴构成的云图。正态云模型是在正态分布和模糊数学概念二者基础上发展起来的全新模型，以此为基础从定性概念实现到定量转换的正态云模型具有普适性。正态云算法定义如下：设U是一个定量论域，可用精确数值表示，而C（Ex，En，He）是U上的定性概念，若存在定量值x（x∈U）是C的一次随机实现，并且其服从以Ex为期望、En'2为方差的正态分布，即x～N（Ex，En'2）；其中，En'又是服从以En为期望、He2为方差的正态分布，即En'～N（En，He2）的一次随机实现；进而，x对C的确定度满足[6]：

u=exp-■ （1）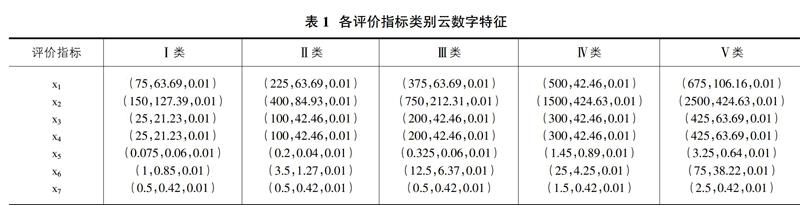

则x在论域U上的分布称为正态云。

1.4 基于云模型的地下水水质评价思路

地下水水质评价中，用1个云滴映射一次具体评价过程。根据地下水质量评价标准，地下水水质可分为5个类别，每个类别可映射为一朵云，文中一个综合云可以表示一个评价指标隶属于某一个水质类别的确定度。主要评价思路如下：

①确定评价指标及其权重。

对可反映评价区域地下水水质情况的指标进行选取，采用熵权法[8]确定各指标权重。

②基于云模型的水质分级。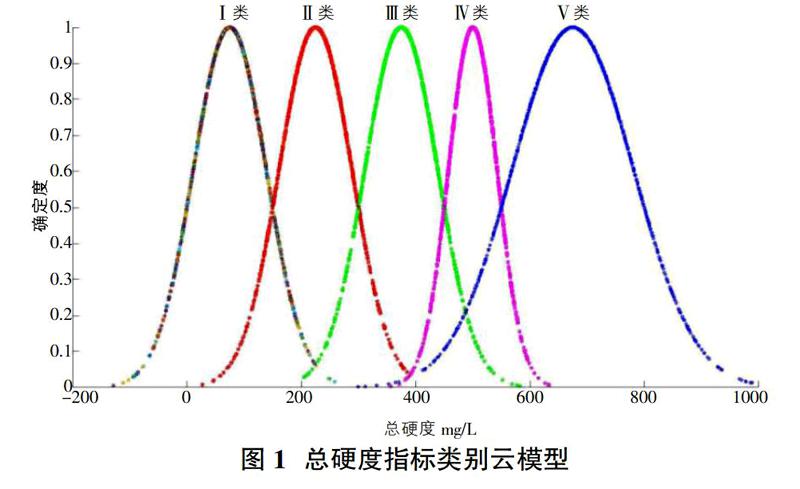

本文分级标准以《地下水质量标准》（GB/T 14848-93）（以下简称《标准》）给出的地下水质量分类指标作为分级标准，计算各类别的三个云数字特征，并生成云图。如对于某评价指标W，其某个分级界限为[a，b]，则3个云数字特征值可由下式得到：

Ex=（a+b）/2En=b-a/2.355He=k （2）

其中：k为常数，可根据经验值进行调整。

③地下水水质确定度计算及综合评价。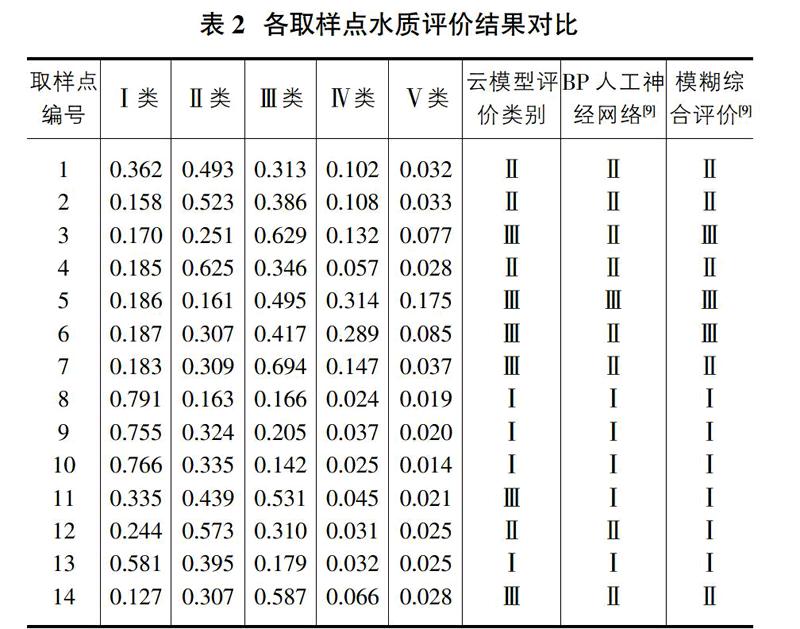

依据各取样点实测数据，采用正态云算法计算各评价指标隶属于各水质类别的确定度。将计算出的确定度与相应的权重相乘，得各取样点地下水水质与各类别的综合确定度，并将确定度最大的类别作为各取样点的地下水水质综合评价类别。

2 工程实例

本文选取文献[9]中西鞍山矿区地下水水质评价作为工程实例，运用云模型理论对其进行评价，并将评价结果与文献结果对比，验证云模型在地下水评价中的有效性。

2.1 确定地下水水质评价指标及其权重

根据文献[9]，分为14个取样点，评价指标为总硬度、溶解性总固体、硫酸盐、氯化物、铁和锰、硝酸盐及氟化物7项指标，分别记为x1～x7，指标实测值见文献[9]。采用熵权法计算指标x1～x7的权重，记为A=[0.142 0.134 0.295 0.147 0.076 0.083 0.123]。

2.2 确定地下水水质类别云模型

依据《标准》中给定的地下水质量分类指标，对其中的缺失边界进行补充，将地下水水质划分为Ⅰ～Ⅴ类5个类别。根据公式（2），计算各水质指标分级标准的云数字特征（Ex，En，He），见表1。

根据表1中计算出的云模型数字特征，采用正向云算法，生成各指标评价类别云图。以总硬度指标为例，设定云滴数为1000，输出云图见图1。

2.3 地下水水质综合评价

根据各取样点实测数据，采用正态云算法计算各评价指标隶属于各水质类别的确定度。由于确定度的计算存在随机性，采用多次计算求平均值的方式计算平均确定度，本次评价计算次数为2000次。将单个指标与各类别的确定度与指标权重向量A相乘后加和，即得各取样点水质与各类别的综合确定度值。根据最大确定度原则，确定各取样点水质类别，并将评价结果与文献[9]評价结果进行对比，见表2。

■

由表2结果可知，8、9、10、13号取样点水质类别为Ⅰ类，1、2、4、12号取样点水质为Ⅱ类，3、5、6、7、11、14号取样点水质为Ⅲ类，本文评价结果与BP人工神经网络方法及模糊综合评价结果基本一致，证明了云模型在地下水水质评价领域的适用性。

3 结论

地下水水质评价所受的不确定性因素较多，存在模糊性及随机性的特点。本文采用云模型方法对地下水水质类别进行评价，实现了定性问题向定量数值的转换，充分考虑到了评价过程中的不确定性因素。通过工程实例的对比，证明了云模型在地下水水质评价领域的适用性，结果较为可靠，为类似不确定性问题的解决提供了一种新的思路。

参考文献：

[1]李名升，张建辉，梁念，林兰钰，李茜，温香彩.常用水环境质量评价方法分析与比较[J].地理科学进展，2012（05）：617-624.

[2]蒋火华，朱建平，梁德华，吴贞丽.综合污染指数评价与水质类别判定的关系[J].中国环境监测，1999（06）：46-48.

[3]樊引琴，刘婷婷，李婳，焦伟晨.物元分析法在黄河水质评价中的应用[J].水资源与水工程学报，2013（02）：166-169.

[4]庞博，李玉霞，童玲.基于灰色聚类法和模糊综合法的水质评价[J].环境科学与技术，2011（11）：185-188.

[5]郝庆杰，江长胜.模糊综合评价法在江安河青羊段水质评价中的应用[J].西南师范大学学报（自然科学版），2010（02）：136-141.

[6]李德毅，杜鹢.不确定性人工智能[M].北京：国防工业出版社，2005.

[7]李健，汪明武，徐鹏，等.基于云模型的围岩稳定性分类[J].岩土工程学报，2014，36（1）：83-87.

[8]章穗，张梅，迟国泰.基于熵权法的科学技术评价模型及其实证研究[J].管理学报，2010（01）：34-42.

[9]潘俊，梁海涛，岳丹丹，赵磊.BP人工神经网络模型在地下水水质评价中的应用[J].供水技术，2015，9（06）：6-11.